RS Aggarwal Solutions for Class 10, maths Chapter 9

Class 10: Maths Chapter 9 solutions. Complete Class 10 Maths Chapter 9 Notes.

Contents

1 RS Aggarwal Solutions for Class 10 Maths Chapter 9–Constructions
2 RS Aggarwal Solutions for Class 10 Maths Chapter 9: Download PDF
3 Chapterwise RS Aggarwal Solutions for Class 10 Maths :
4 About RS Aggarwal Class 10 Book
5 FAQs
6 Read More

RS Aggarwal Solutions for Class 10 Maths Chapter 9–Constructions

RS Aggarwal 10th Maths Chapter 9, Class 10 Maths Chapter 9 solutions

Page No 522:

Question 1:

Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that $\frac{AP}{AB} = \frac{3}{5}$ . [CBSE 2011]

Answer:

Steps of Construction:

Step 1. Draw a line segment AB = 7 cm.

Step 2. Draw a ray AX, making an acute angle $∠$ BAX.

Step 3. Along AX, mark 5 points (greater of 3 and 5) A₁, A₂, A₃, A₄ and A₅ such that

AA₁= A₁A₂ = A₂A₃= A₃A₄ = A₄A₅

Step 4. Join A₅B.

Step 5. From A₃, draw A₃P parallel to A₅B (draw an angle equal to $∠$ AA₅B), meeting AB in P.

Here, P is the point on AB such that $\frac{AP}{PB} = \frac{3}{2}$ or $\frac{AP}{AB} = \frac{3}{5}$ .

Page No 522:

Question 2:

(i) Draw a line segment of length 8 cm and divide it internally in the ratio 4 : 5. [CBSE 2017]
(ii) Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.

Answer:

(i) Steps of Construction:

Step 1. Draw a line segment AB = 8 cm

Step 2. Draw a ray AX, making an acute angle $∠$ BAX.

Step 3. Along AX, mark (4 + 5 =) 9 points A₁, A₂, A₃, A₄, A₅, A₆, A₇, A₈ and A9 such that

AA₁= A₁A₂ = A₂A₃= A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇ = A₇A₈= A₈A₉

Step 4. Join A₉B.

Step 5. From A₄, draw A₄D parallel to A₉B (draw an angle equal to $∠$ AA₉B), meeting AB in D.

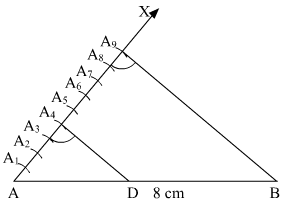
Here, D is the point on AB which divides it in the ratio 4 : 5.

(ii) Steps of Construction:

Step 1. Draw a line segment AB = 7.6 cm

Step 2. Draw a ray AX, making an acute angle $∠$ BAX.

Step 3. Along AX, mark (5 + 8 =) 13 points A₁, A₂, A₃, A₄, A₅, A₆, A₇, A₈, A₉, A₁₀, A₁₁, A₁₂ and A₁₃ such that

AA₁= A₁A₂ = A₂A₃= A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇ = A₇A₈= A₈A₉ = A₉A₁₀= A₁₀A₁₁ = A₁₁A₁₂ = A₁₂A₁₃

Step 4. Join A₁₃B.

Step 5. From A₅, draw A₅P parallel to A₁₃B (draw an angle equal to $∠$ AA₁₃B), meeting AB in P.

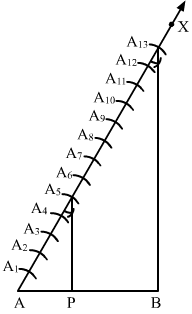
Here, P is the point on AB which divides it in the ratio 5 : 8.

∴ Length of AP = 2.9 cm (Approx)

Length of BP = 4.7 cm (Approx)

Page No 522:

Question 3:

Construct a ∆PQR, in which PQ = 6 cm, QR = 7 cm and PR = 8 cm. Then, construct another triangle whose sides are $\frac{4}{5}$ times the corresponding sides of ∆PQR. [CBSE 2013, 14]

Answer:

Steps of Construction

Step 1. Draw a line segment QR = 7 cm.

Step 2. With Q as centre and radius 6 cm, draw an arc.

Step 3. With R as centre and radius 8 cm, draw an arc cutting the previous arc at P.

Step 4. Join PQ and PR. Thus, ∆PQR is the required triangle.

Step 5. Below QR, draw an acute angle $∠$ RQX.

Step 6. Along QX, mark five points R₁, R₂, R₃, R₄and R₅such that QR₁ = R₁R₂ = R₂R₃ = R₃R₄= R₄R₅.

Step 7. Join RR₅.

Step 8. From R₄, draw R₄R’ || RR₅ meeting QR at R’.

Step 9. From R’, draw P’R’ || PR meeting PQ in P’.

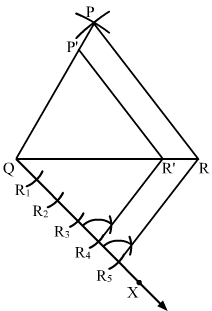
Here, ∆P’QR’ is the required triangle, each of whose sides are $\frac{4}{5}$ times the corresponding sides of ∆PQR.

Page No 522:

Question 4:

Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are $\frac{7}{5}$ of the corresponding sides of first triangle.

Answer:

Steps of Construction :

Step 1. Draw a line segment BC = 4 cm.
Step 2. With B as centre, draw an angle of 90^o.
Step 3. With B as centre and radius equal to 3 cm, cut an arc at the right angle and name it A.
Step 4. Join AB and AC.
Thus, △ ABC is obtained .
Step 5. Extend BC to D, such that BD = $\frac{7}{5}$ BC = $\frac{7}{5}$ (4) cm = 5.6 cm.
Step 6. Draw DE ∥ CA, cutting AB produced to E.

Thus, △EBD is the required triangle, each of whose sides is $\frac{7}{5}$ the corresponding sides of ∆ABC.

Page No 523:

Question 5:

Construct a ΔABC with BC = 6 cm, ∠B = 60° and AB = 5 cm. Construct another triangle whose sides are $\frac{3}{4}$ times the corresponding sides of ΔABC.

Answer:

Given: In ΔABC,
BC = 6 cm,
∠B = 60°
AB = 5 cm

Steps of construction:
(1) Draw a line segment AB = 5 cm.
(2) From the point B, draw an ∠ABY = 60°
(3) Taking B as center, 6 cm radius, draw an arc on the ray BY,
Let the point where the arc intersects the ray named as C.
(4) Join AC.

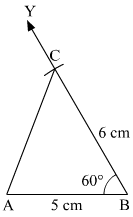
Hence, ΔABC is the required triangle.

Now, we construct another triangle whose sides are $\frac{3}{4}$ times the corresponding sides of ΔABC.

Steps of construction:
(1) Draw any ray BX making an acute angle with BA on the side opposite to the vertex C.
(2) Mark four points B₁, B₂, B₃and B₄ on BX, so that BB₁ = B₁B₂ = B₂B₃ = B₃B₄.
(3) Join B₄A and draw a line through B₃parallel to B₄A to intersect AB at A’.
(4) Draw a line through A’ parallel to AC to intersect BC at C’.

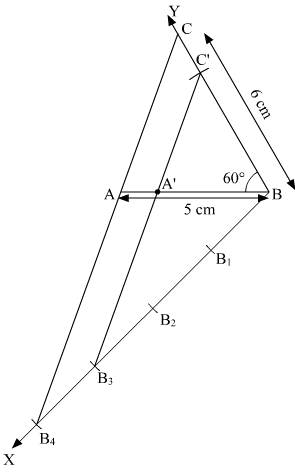
Hence, ΔA’BC’ is the required triangle.

Page No 523:

Question 6:

Construct a ∆ABC in which AB = 6 cm, $∠$ A = 30º and $∠$ B = 60º. Construct another ∆AB’C’ similar to ∆ABC with base
AB’ = 8 cm. [CBSE 2015]

Answer:

Steps of Construction

Step 1. Draw a line segment AB = 6 cm.

Step 2. At A, draw $∠$ XAB = 30º.

Step 3. At B, draw $∠$ YBA = 60º. Suppose AX and BY intersect at C.

Thus, ∆ABC is the required triangle.

Step 4. Produce AB to B’ such that AB’ = 8 cm.

Step 5. From B’, draw B’C’ || BC meeting AX at C’.

Here, ∆AB’C’ is the required triangle similar to ∆ABC.

Page No 523:

Question 7:

Construct a ∆ABC in which BC = 8 cm, $∠$ B = 45º and $∠$ C = 60º. Construct another triangle similar to ∆ABC such that its sides are $\frac{3}{5}$ of the corresponding sides of ∆ABC. [CBSE 2010, ’12, ’14]

Answer:

Steps of Construction

Step 1. Draw a line segment BC = 8 cm.

Step 2. At B, draw $∠$ XBC = 45º.

Step 3. At C, draw $∠$ YCB = 60º. Suppose BX and CY intersect at A.

Thus, ∆ABC is the required triangle.

Step 4. Below BC, draw an acute angle $∠$ ZBC.

Step 5. Along BZ, mark five points Z₁, Z₂, Z₃, Z₄and Z₅such that BZ₁ = Z₁Z₂ = Z₂Z₃ = Z₃Z₄ = Z₄Z₅.

Step 6. Join CZ₅.

Step 7. From Z₃, draw Z₃C’ || CZ₅ meeting BC at C’.

Step 8. From C’, draw A’C’ || AC meeting AB in A’.

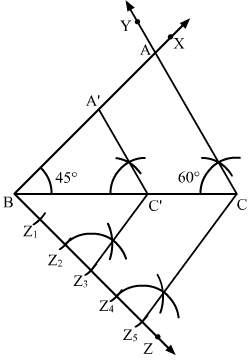
Here, ∆A’BC’ is the required triangle whose sides are $\frac{3}{5}$ of the corresponding sides of ∆ABC.

Page No 523:

Question 8:

To construct a triangle similar to ∆ABC in which BC = 4.5 cm, $∠$ B = 45º and $∠$ C = 60º, using a scale factor of $\frac{3}{7}$ , BC will be divided in the ratio

(a) 3 : 4 (b) 4 : 7 (c) 3 : 10 (d) 3 : 7 [CBSE 2012]

Answer:

To construct a triangle similar to ∆ABC in which BC = 4.5 cm, $∠$ B = 45º and $∠$ C = 60º, using a scale factor of $\frac{3}{7}$ , BC will be divided in the ratio 3 : 4.

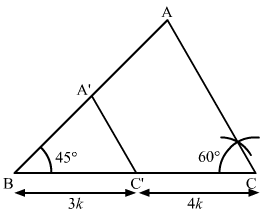
Here, ∆ABC ∼ ∆A’BC’

BC’ : C’C = 3 : 4

or BC’ : BC = 3 : 7

Hence, the correct answer is option A.

Page No 523:

Question 9:

Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are $1 \frac{1}{2}$ times the corresponding sides of the isosceles triangle.

Answer:

Steps of Construction

Step 1. Draw a line segment BC = 8 cm.

Step 2. Draw the perpendicular bisector XY of BC, cutting BC at D.

Step 3. With D as centre and radius 4 cm, draw an arc cutting XY at A.

Step 4. Join AB and AC. Thus, an isosceles ∆ABC whose base is 8 cm and altitude 4 cm is obtained.

Step 5. Extend BC to E such that BE = $\frac{3}{2}$ BC = $\frac{3}{2} \times 8$ cm = 12 cm.

Step 6. Draw EF || CA, cutting BA produced in F.

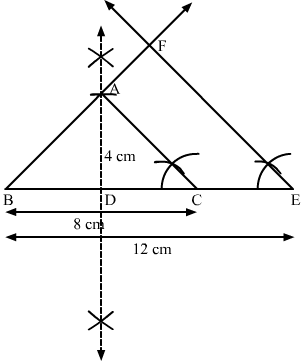
Here, ∆BEF is the required triangle similar to ∆ABC such that each side of ∆BEF is $1 \frac{1}{2} (or \frac{3}{2})$ times the corresponding side of ∆ABC.

Page No 523:

Question 10:

Draw a right triangle in which sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then, construct another triangle whose sides are $\frac{5}{3}$ times the corresponding sides of the given triangle. [CBSE 2011]

Answer:

Steps of Construction

Step 1. Draw a line segment BC = 3 cm.

Step 2. At B, draw $∠$ XBC = 90º.

Step 3. With B as centre and radius 4 cm, draw an arc cutting BX at A.

Step 4. Join AC. Thus, a right ∆ABC is obtained.

Step 5. Extend BC to D such that BD = $\frac{5}{3}$ BC = $\frac{5}{3} \times 3$ cm = 5 cm.

Step 6. Draw DE || CA, cutting BX in E.

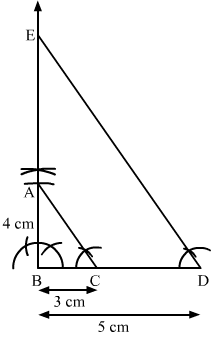
Here, ∆BDE is the required triangle similar to ∆ABC such that each side of ∆BDE is $\frac{5}{3}$ times the corresponding side of ∆ABC.

Page No 529:

Question 1:

Draw a circle of radius 3 cm. From a point P, 7 cm away from the centre of the circle, draw two tangents to the circle. Also, measure the lengths of the tangents. [CBSE 2010]

Answer:

Steps of Construction

Step 1. Draw a circle with O as centre and radius 3 cm.

Step 2. Mark a point P outside the circle such that OP = 7 cm.

Step 3. Join OP. Draw the perpendicular bisector XY of OP, cutting OP at Q.

Step 4. Draw a circle with Q as centre and radius PQ (or OQ), to intersect the given circle at the points T and T’.

Step 5. Join PT and PT’.

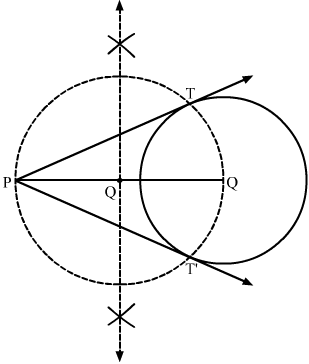
Here, PT and PT’ are the required tangents.

PT = PT’ = 6.3 cm (Approx)

Page No 529:

Question 2:

Draw two tangents to a circle of radius 3.5 cm from a point P at a distance of 6.2 cm from its centre.

Answer:

Steps of Construction

Step 1. Draw a circle with O as centre and radius 3.5 cm.

Step 2. Mark a point P outside the circle such that OP = 6.2 cm.

Step 3. Join OP. Draw the perpendicular bisector XY of OP, cutting OP at Q.

Step 4. Draw a circle with Q as centre and radius PQ (or OQ), to intersect the given circle at the points T and T’.

Step 5. Join PT and PT’.

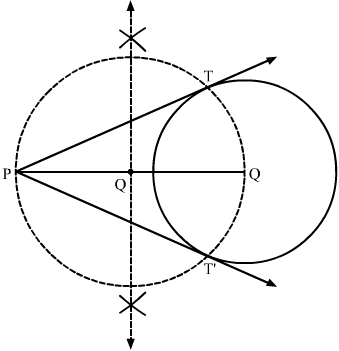
Here, PT and PT’ are the required tangents.

Page No 529:

Question 3:

Draw a circle of radius 3 cm. Take two points P and Q on one of its diameters extended on both sides, each at a distance of 7 cm on opposite sides of its centre. Draw tangents to the circle from these two points P and Q. [CBSE 2017]

Answer:

Steps of Construction

Step 1. Draw a circle with O as centre and radius 3 cm.

Step 2. Mark a point P and Q on one of its diameters extended on both sides outside the circle such that OP = OQ = 7 cm.

Step 3. Join OP and OQ. Draw the perpendicular bisector XY of OP and X’Y’ of OQ, cutting OP at L and OQ at M.

Step 4. Draw a circle with L as centre and radius PL (or OL), to intersect the given circle at the points A and B. Draw another circle with M as centre and radius MQ (or OM), to intersect the given circle at the points C and D.

Step 5. Join PA and PB. Join QC and QD.

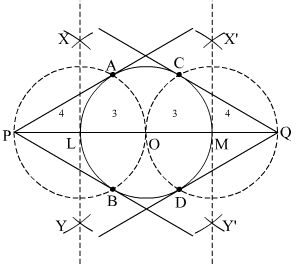
Here, PA, PB and QC, QD are the required tangents.

Page No 529:

Question 4:

Draw a circle with centre O and radius 4 cm. Draw any diameter AB of this circle. Construct tangents to the circle at each of the two end points of the diameter AB.

Answer:

Steps of Construction

Step 1. Draw a circle with centre O and radius 4 cm.

Step 2. Draw any diameter AOB of the circle.

Step 3. At A, draw $∠$ OAX = 90º. Produce XA to Y.

Step 4. At B, draw $∠$ OBX’ = 90º. Produce X’B to Y’.

Here, XAY and X’BY’ are the tangents to the circle at the end points of the diameter AB.

Page No 530:

Question 5:

Draw a circle with the help of a bangle. Take any point P outside the circle. Construct the pair of tangents from the point P to the circle.

Answer:

Steps of Construction

Step 1. Draw a circle with the help of a bangle.

Step 2. Mark a point P outside the circle.

Step 3. Through P, draw a secant PAB to intersect the circle at A and B.

Step 4. Produce AP to C such that PA = PC.

Step 5. Draw a semicircle with CB as diameter.

Step 6. Draw PD ⊥ BC, intersecting the semicircle at D.

Step 7. With P as centre and PD as radius, draw arcs to intersect the circle at T and T’.

Step 8. Join PT and PT’.

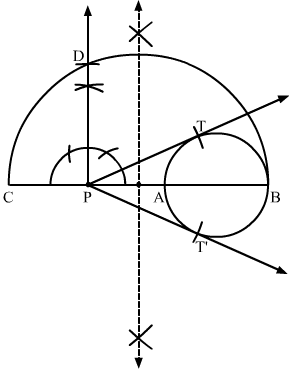
Here, PT and PT’ are the required pair of tangents.

Page No 530:

Question 6:

Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle. [CBSE 2014]

Answer:

Steps of Construction

Step 1. Draw a line segment AB = 8 cm.

Step 2. With A as centre and radius 4 cm, draw a circle.

Step 3. With B as centre and radius 3 cm, draw another circle.

Step 4. Draw the perpendicular bisector XY of AB, cutting AB at C.

Step 5. With C as centre and radius AC (or BC), draw a circle intersecting the circle with centre A at P and P’; and the circle with centre B at Q and Q’.

Step 6. Join BP and BP’. Also, join AQ and AQ’.

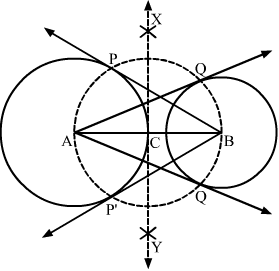
Here, AQ and AQ’ are the tangents from A to the circle with centre B. Also, BP and BP’ are the tangents from B to the circle with centre A.

Page No 530:

Question 7:

Draw a circle of radius 4.2 cm. Draw a pair of tangents to this circle inclined to each other at an angle of 45°.

Answer:

Steps of Construction:

Step 1. Draw a circle with centre O and radius = 4.2 cm.
Step 2. Draw any diameter AOB of this circle.
Step 3. Construct $∠ B O C = 45 °$ , such that the radius OC meets the circle at C.
Step 4. Draw AM $⊥ A B and C N ⊥ O C .$
AM and CN intersect at P.

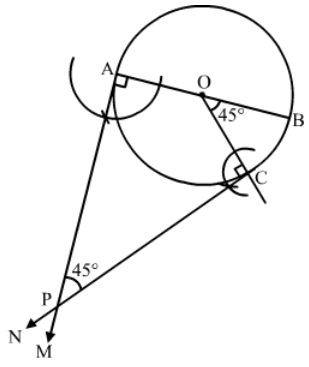
Thus, PA and PC are the required tangents to the given circle inclined at an angle of 45^o.

Page No 530:

Question 8:

Write the steps of construction for drawing a pair of tangents to a circle of radius 3 cm, which are inclined to each other at an angle of 60º.
[CBSE 2011, ’12, ’14]

Answer:

Steps of Construction

Step 1. Draw a circle with centre O and radius 3 cm.

Step 2. Draw any diameter AOB of the circle.

Step 3. Construct $∠$ BOC = 60º such that radius OC cuts the circle at C.

Step 4. Draw AM ⊥ AB and CN ⊥ OC. Suppose AM and CN intersect each other at P.

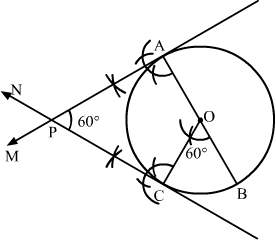
Here, AP and CP are the pair of tangents to the circle inclined to each other at an angle of 60º.

Page No 530:

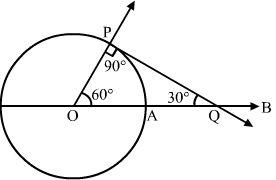
Question 9:

Draw a circle of radius 3 cm. Draw a tangent to the circle making an angle of 30° with a line passing through the centre.

Answer:

Steps Of construction:

Step 1. Draw a circle with centre O and radius 3 cm.
Step 2. Draw radius OA and produce it to B.
Step 3. Make $∠ A O P = 60 °$ .
Step 4. Draw PQ $⊥ O P$ , meeting OB at Q.
Step 5. Then, PQ is the desired tangent, such that $∠ O Q P = 30 °$ .

Page No 530:

Question 10:

Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.

Answer:

Steps of Construction

Step 1. Mark a point O on the paper.

Step 2. With O as centre and radii 4 cm and 6 cm, draw two concentric circles.

Step 3. Mark a point P on the outer circle.

Step 4. Join OP.

Step 5. Draw the perpendicular bisector XY of OP, cutting OP at Q.

Step 6. Draw a circle with Q as centre and radius OQ (or PQ), to intersect the inner circle in points T and T’.

Step 7. Join PT and PT’.

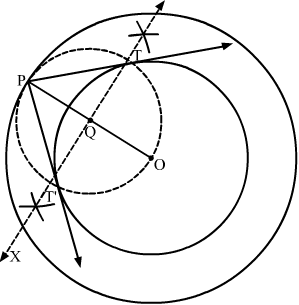
Here, PT and PT’ are the required tangents.

PT = PT’ = 4.5 cm (Approx)

Verification by actual calculation

Join OT to form a right ∆OTP. (Radius is perpendicular to the tangent at the point of contact)

In right ∆OTP,

${OP}^{2} = {OT}^{2} + {PT}^{2} (Pythagoras Theorem) \Rightarrow PT = \sqrt{{OP}^{2} - {OT}^{2}} \Rightarrow PT = \sqrt{6^{2} - 4^{2}} = \sqrt{36 - 16} = \sqrt{20} \approx 4.5 cm (OP = 6 cm and OT = 4 cm)$

Page No 530:

Question 11:

Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on the outer circle, construct the pair of tangents to the inner circle. [CBSE 2017]

Answer:

Steps of Construction

Step 1. Mark a point O on paper.

Step 2. Taking O as a centre, draw two concentric circles of radius 3 cm and 5 cm. Mark any random point P on outer circle.

Step 3. Join OP and draw its perpendicular bisector which meets OP at M.

Step 4. Draw a circle with M as centre and radius PM (or OM), to intersect the inner circle at the points A and B.

Step 5. Join PA and PB.

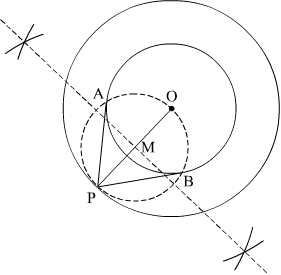
Here, PA and PB are the required tangents.

Page No 530:

Question 12:

Write the steps of construction to construct the tangents to a circle from an external point.

Answer:

Steps of Construction

Step 1. Draw a circle with O as centre and some radius.

Step 2. Mark a point P outside the circle. Join OP.

Step 3. Draw the perpendicular bisector of OP cutting it at M.

Step 4. Draw another circle with M as centre and radius MP (or OM), to intersect the given circle at the points A and B.

Step 5. Join PA and PB.

Here, PA and PB are the required tangents.

Page No 530:

Question 1:

Draw a line segment AB of length 5.4 cm. Divide it into six equal parts. Write the steps of construction.

Answer:

Steps of Construction :

Step 1 . Draw a line segment AB = 5.4 cm.
Step 2. Draw a ray AX, making an acute angle, $∠ B A X$ .∠BAX.
Step 3. Along AX, mark 6 points A₁, A₂_, A₃_,A₄_, A₅, A₆such that,
AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅= A₅A₆ .
Step 4. Join A₆B.
Step 5. Draw A₁C ∥A₂D, A₃D, A₄F and A₅G .

Thus, AB is divided into six equal parts.

Page No 530:

Question 2:

Draw a line segment AB of length 6.5 cm and divide it in the ratio 4 : 7. Measure each of the two parts.

Answer:

Steps of Construction :

Step 1 . Draw a line segment AB = 6.5 cm.
Step 2. Draw a ray AX, making an acute angle $∠ B A X$ .
Step 3. Along AX, mark (4+7) =11 points A₁, A₂_, A₃_,A₄_, A₅, A₆, A₇, A₈, A₉, A₁₀, A₁₁_,such that
            AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅= A₅A₆ = A₆A₇ = A₇A₈ = A₈A₉ = A₉A₁₀ = A₁₀A₁₁
Step 4. Join A₁₁B.
Step 5. From A₄_,draw A₄C $∥$ A₁₁B, meeting AB at C.
            Thus, C is the point on AB, which divides it in the ratio 4:7.

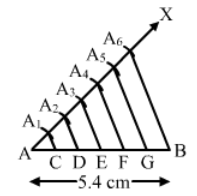
Thus, AC : CB = 4:7
From the figure, AC = 2.36 cm
                           CB = 4.14 cm

Page No 531:

Question 3:

Construct a ∆ABC, in which BC = 6.5 cm, AB = 4.5 cm and ∠ABC = 60°. Construct a triangle similar to this triangle whose sides are $\frac{3}{4}$ the corresponding sides of ∆ABC.

Answer:

Steps of Construction :

Step 1. Draw a line segment BC = 6.5 cm.
Step 2. With B as centre, draw an angle of 60^o.
Step 3. With B as centre and radius equal to 4.5 cm, draw an arc, cutting the angle at A.
Step 4. Join AB and AC.
Thus, △ ABC is obtained .
Step 5. Below BC, draw an acute $∠ C B X$ .
Step 6. Along BX, mark off four points B₁, B₂, B₃, B₄, such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄_.
Step 7. Join B₄C.
Step 8. From B₃, draw B₃D ∥ B₄C, meeting BC at D.
Step 9. From D, draw DE ∥ CA, meeting AB at E.

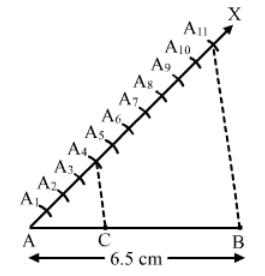
Thus, △ EBD is the required triangle, each of whose sides is $\frac{3}{4}$ the corresponding sides of ∆ABC.

Page No 531:

Question 4:

Construct a ∆ABC, in which BC = 5 cm, ∠C = 60° and altitude from A is equal to 3 cm. Construct a ∆ADE similar to ∆ABC, such that each side of ∆ADE is $\frac{3}{2}$ times the corresponding side of ∆ABC. Write the steps of construction.

Answer:

Steps of Construction :

Step 1. Draw a line l .
Step 2. Draw an angle of 90^o at M on l .
Step 3. Cut an arc of radius 3 cm on the perpendicular. Mark the point as A.
Step 4. With A as centre, make an angle of 30^oand let it cut l at C. We get $∠ A C B = 60 °$ .
Step 5. Cut an arc of 5 cm from C on l and mark the point as B.
Step 6. Join AB.
Thus, △ABC is obtained .
Step 7. Extend AB to D, such that BD = $\frac{1}{2}$ BC.
Step 8. Draw DE $∥ B C$ , cutting AC produced to E.

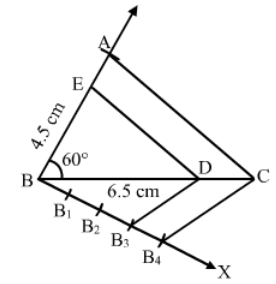
Then, △ADE is the required triangle, each of whose sides is $\frac{3}{2}$ of the corresponding sides of △ABC.

Page No 531:

Question 5:

Construct an isosceles triangle whose base is 9 cm and altitude 5 cm. Construct another triangle whose sides are $\frac{3}{4}$ the corresponding sides of the first isosceles triangle.

Answer:

Steps of Construction :

Step 1. Draw a line segment BC = 9 cm.
Step 2. With B as centre, draw an arc each above and below BC.
Step 3. With C as centre, draw an arc each above and below BC.
Step 4. Join their points of intersection to obtain the perpendicular bisector of BC. Let it intersect BC at D.
Step 5. From D, cut an arc of radius 5 cm and mark the point as A.
Step 6. Join AB and AC.
Thus, △ABC is obtained .
Step 5. Below BC, make an acute $∠ C B X$ .
Step 6. Along BX, mark off four points B₁, B₂, B₃, B₄, such that BB₁=B₁B₂ = B₂B₃ = B₃B₄_.
Step 7. Join B₄C.
Step 8. From B₃, draw B₃E ∥ B₄C, meeting BC at E.
Step 9. From E, draw EF ∥ CA, meeting AB at F.

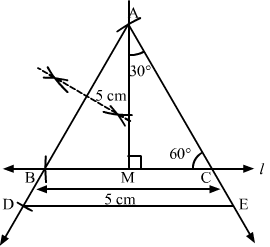
Thus, △FBE is the required triangle, each of whose sides is $\frac{3}{4}$ the corresponding sides of the first triangle.

Page No 531:

Question 6:

Draw ∆ABC, right-angled at B, such that AB = 3 cm and BC = 4 cm. Now, construct a triangle similar to ∆ABC, each of whose sides is $\frac{7}{5}$ times the corresponding sides of ∆ABC.

Answer:

Page No 531:

Question 7:

Draw a circle of radius 4.8 cm. Take a point P on it. Without using the centre of the circle, construct a tangent at the point P. Write the steps of construction.

Answer:

Steps of Construction :

Step 1. Draw a circle of radius 4.8 cm.
Step 2. Mark a point P on it.
Step 3. Draw any chord PQ.
Step 4. Take a point R on the major arc QP.
Step 5. Join PR and RQ.
Step 6. Draw $∠ Q P T = ∠ P R Q$
Step 7. Produce TP to T’, as shown in the figure.

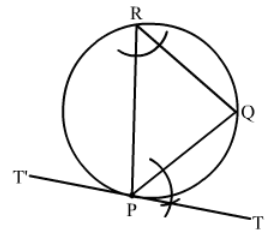
T’PT is the required tangent.

Page No 531:

Question 8:

Draw a circle of radius 3.5 cm. Draw a pair of tangents to this circle, which are inclined to each other at an angle of 60°. Write the steps of construction.

Answer:

Steps of Construction:

Step 1. Draw a circle with centre O and radius = 3.5 cm.
Step 2. Draw any diameter AOB of this circle.
Step 3. Construct $∠ B O C = 60 °$ , such that the radius OC meets the circle at C.
Step 4. Draw MA $⊥ A B and N C ⊥ O C .$ ⊥AB and CN⊥OC.
Let AM and CN intersect at P.

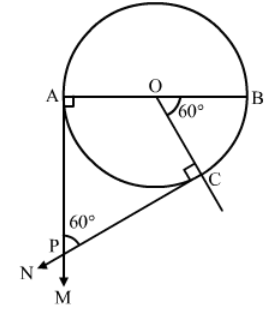
Then, PA and PC are the required tangents to the given circle that are inclined at an angle of 60^o.

Page No 531:

Question 9:

Draw a circle of radius 4 cm. Draw a tangent to the circle, making an angle of 60° with a line passing through the centre.

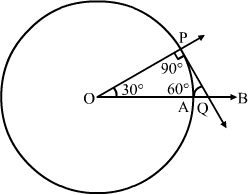
Answer:

Steps Of construction:

Step 1. Draw a circle with centre O and radius 4 cm.
Step 2. Draw radius OA and produce it to B.
Step 3. Make $∠ A O P = 30 °$ ∠AOP = 60°.
Step 4. Draw PQ $⊥ O P$ , meeting OB at Q.
Step 5. Then, PQ is the desired tangent, such that $∠ O Q P = 60 °$ .

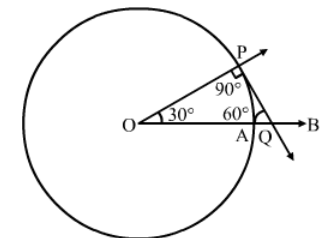∠OQP = 30°

Page No 531:

Question 10:

Draw two concentric circles of radii 4 cm and 6 cm. Construct a tangent to the smaller circle from a point on the larger circle. Measure the length of this tangent.

Answer:

Steps of Construction :

Step 1. Draw a circle with O as centre and radius 6 cm.
Step 2. Draw another circle with O as centre and radius 4 cm.
Step 2 . Mark a point P on the circle with radius 6 cm.
Step 3. Join OP and bisect it at M.
Step 4. Draw a circle with M as centre and radius equal to MP to intersect the given circle with radius 4 cm at points T and T^‘.
Step 5. Join PT and P T^‘.

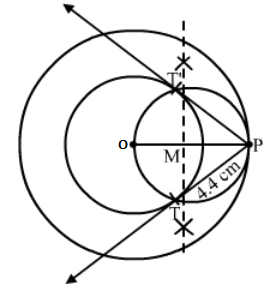
Thus, PT or P T^‘are the required tangents and measure 4.4 cm each.

RS Aggarwal Solutions for Class 10 Maths Chapter 9: Download PDF

RS Aggarwal Solutions for Class 10 Maths Chapter 9–Constructions

Download PDF: RS Aggarwal Solutions for Class 10 Maths Chapter 9–Constructions PDF

Chapterwise RS Aggarwal Solutions for Class 10 Maths :

About RS Aggarwal Class 10 Book

Investing in an R.S. Aggarwal book will never be of waste since you can use the book to prepare for various competitive exams as well. RS Aggarwal is one of the most prominent books with an endless number of problems. R.S. Aggarwal’s book very neatly explains every derivation, formula, and question in a very consolidated manner. It has tonnes of examples, practice questions, and solutions even for the NCERT questions.

He was born on January 2, 1946 in a village of Delhi. He graduated from Kirori Mal College, University of Delhi. After completing his M.Sc. in Mathematics in 1969, he joined N.A.S. College, Meerut, as a lecturer. In 1976, he was awarded a fellowship for 3 years and joined the University of Delhi for his Ph.D. Thereafter, he was promoted as a reader in N.A.S. College, Meerut. In 1999, he joined M.M.H. College, Ghaziabad, as a reader and took voluntary retirement in 2003. He has authored more than 75 titles ranging from Nursery to M. Sc. He has also written books for competitive examinations right from the clerical grade to the I.A.S. level.

FAQs

Why must I refer to the RS Aggarwal textbook?
RS Aggarwal is one of the most important reference books for high school grades and is recommended to every high school student. The book covers every single topic in detail. It goes in-depth and covers every single aspect of all the mathematics topics and covers both theory and problem-solving. The book is true of great help for every high school student. Solving a majority of the questions from the book can help a lot in understanding topics in detail and in a manner that is very simple to understand. Hence, as a high school student, you must definitely dwell your hands on RS Aggarwal!

Why should you refer to RS Aggarwal textbook solutions on Indcareer?
RS Aggarwal is a book that contains a few of the hardest questions of high school mathematics. Solving them and teaching students how to solve questions of such high difficulty is not the job of any neophyte. For solving such difficult questions and more importantly, teaching the problem-solving methodology to students, an expert teacher is mandatory!

Does IndCareer cover RS Aggarwal Textbook solutions for Class 6-12?
RS Aggarwal is available for grades 6 to 12 and hence our expert teachers have formulated detailed solutions for all the questions of each edition of the textbook. On our website, you’ll be able to find solutions to the RS Aggarwal textbook right from Class 6 to Class 12. You can head to the website and download these solutions for free. All the solutions are available in PDF format and are free to download!