RS Aggarwal Solutions for Class 10 Maths Chapter 4–Quadratic Equations

Class 10: Maths Chapter 4 solutions. Complete Class 10 Maths Chapter 4 Notes.

RS Aggarwal Solutions for Class 10 Maths Chapter 4–Quadratic Equations

RS Aggarwal 10th Maths Chapter 4, Class 10 Maths Chapter 4 solutions

Exercise 10A Solutions

Question 1:

(i)   x²-x+3=0 is a quadratic polynomial.
∴  x²-x+3=0 is a quadratic equation.

(ii) 2x²+ 52x-√3=0
⇒ 4x²+5x-2√3=0
Clearly is 4x²+5x-2√3=0 a quadratic polynomial.
∴ 2x²+ 52x-√3=0 is a quadratic equation.

(iii) √2x²+7x+5√2=0 is a quadratic polynomial.
∴ √2x²+7x+5√2=0 is a quadratic equation.

(iv)13x²+15x-2=0
⇒ 5x²+3x-2=0
Clearly, 5x²+3x-2=0 is a quadratic equation.
13x²+15 is a quadratic equation.

(v) x²-3x-√x+4=0 is not a quadratic polynomial since it contains √x, in which power 1/2 of x is not an integer.
∴ x²-3x-√x+4=0 is not a quadratic equation.

(vi) x-6x=3
⇒ x²-3x-6 =0
And (x²-3x-6)Being a polynomial of degree 2, it is a quadratic polynomial.
Hence, x-6x=3 is a quadratic equation.

(vii) x+2x= x²
⇒ x³-x²-2 =0
And (x³-x²-2 =0) being a polynomial of degree 3, it is not a quadratic polynomial.
Hence, x+2x= x² is not a quadratic equation.

(viii) x2−1×2=5 ⇒ x⁴ -1=5x²
⇒x⁴-5x²-1 =0
And (x⁴-5x²-1 =0) being a polynomial of degree 4.
Hence x2−1×2=5 is not a quadratic equation.

Question 2:
The given equation is 3x²+2x-1=0
(i) On substituting x = -1 in the equation, we get

(ii) On substituting x=13 in the equation, we get

(iii) On substituting x=−12 in the equation , we get

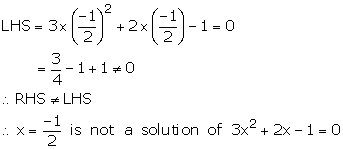
Question 3:
Since x = 1 is a solution of x²+kx+3=0 it must satisfy the equation.

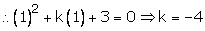
Hence the required value of k = -4
Question 4:
Since x=34 is a root of  ax²+bx-6=0, we have

Again x = -2 being a root of ax²+bx-6=0, we have

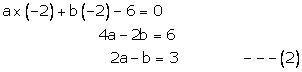
Multiplying (2) by 4 adding the result from (1), we get
11a = 44 ⇒ a = 4
Putting a = 4 in (1), we get

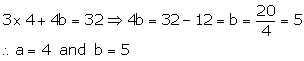
Question 5:

Question 6:

Question 7:

Hence, 9 and -9 are the roots of the equation 3x²-243=0.
Question 8:

Hence, -5 and -7 are the roots of x²+12x+35=0.
Question 9:

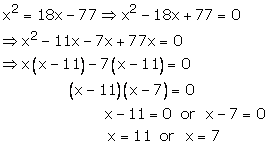
Hence, 11 and 7 are the roots of equation x²=18x-77
Question 10:

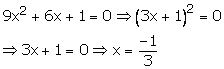
Hence, x=−13 is the repeated root of the equation 9x²+6x+1=0
Question 11:

Hence,  is the repeated root of the equation
Question 12:

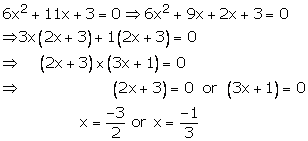
Hence, x=−32, x=−12are the roots of 6x²+11x+3=0
Question 13:

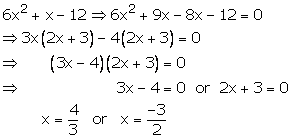
Hence, x=43 and x=−32 are the roots of equation 6x²+x-12=0

Question 14:

Hence, x=−13 and 1 are the roots of the equation 3x²-2x-1=0.
Question 15:

Hence, x=23 and x=−12are the roots of equation 6x²-x-2=0.
Question 16:

Hence, x=−116 and x=23 are the roots of 48x²-13x-1=0.
Question 17:

Hence, x=−53 and x=-2 are the roots of the equation 3x²+11x+10=0
Question 18:

Hence,x=254 and x=-4 are the roots of the equation 4x²-9x=100.
Question 19:

Hence,  x=49 and 2 are the roots of the equation 9x²-22+8=0
Question 20:

Hence,  x=75 and x=−43 are the roots of the given equation 15x²-28=x.
Question 21:

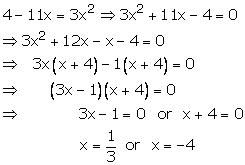
Hence, x=13 and -4 are the roots of given equation .
Question 22:

Hence, 1 and  √2 are the roots of the given equation
Question 23:

Question 24:

Question 25:

Hence, −7√3 and 7√7 are the roots of given equation.
Question 26:

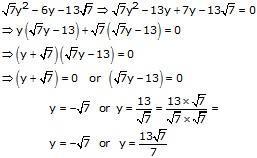
Hence, -√7 and 137√7 are the roots of given equation.
Question 27:

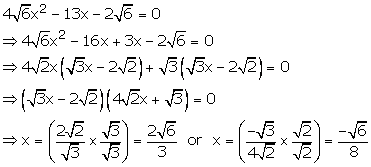
Hence, 26√3 and  −6√8are the roots of given equation.
Question 28:

Hence, 5 and −75are the roots of given equation
Question 29:

Hence, −15 and 12are the roots of given equation.
Question 30:

Hence, 2 and  12 are the roots of given equation.
Question 31:

Hence, −ba and cb are the roots of given equation.
Question 32:

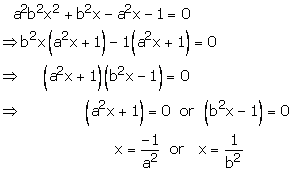
Hence, −1a2 and 1b2are the roots of given equation.
Question 33:

Hence, 3a4b and −2b3a are the roots of given equation.
Question 34:

Hence, a22 and b22are the roots of given equation.
Question 35:

Hence, 2 and 1 are the roots of the given equation
Question 36:

Hence, -9 and 7 are the roots of the given equation
Question 37:

Hence, -4 and 94 are the roots of the given equation
Question 38:

Hence  4013 and 6 are the roots of the given equation
Question 39:

Hence, 4 and −29 are the roots of the given equation
Question 40:

Hence, 3 and 43 are the roots of the given equation.
Question 41:

Hence, 5 and 12 are the roots of the given equation.
Question 42:
Putting 

 the given equation become

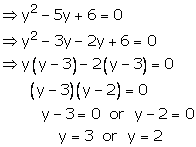
Case I:

Case II:

Hence, −32 and -2 are the roots of the given equation
Question 43:

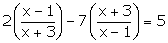
Putting 

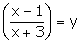
 the given equation become

Case I:

Case II:

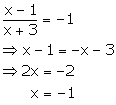
Hence, -1 and −235 are the roots of the given equation
Question 44:
On putting 

 the given equation become

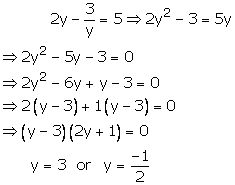
Case I:

Case II:

Hence, -10 and −15 are the roots of the given equation.
Question 45:
Putting 

 the given equation become

Case I:

Case II:

Hence, -1 and 18 are the roots of the given equation
Question 46:
The given equation

Hence, (a+b) and (a+b)2 is the roots of the given equation
Question 47:

Hence, a+bab and 2a+b are the roots of the given equation
Question 48:

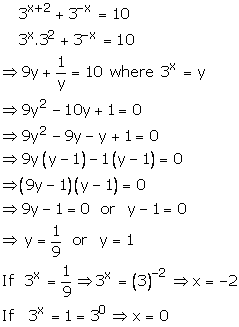
Hence, -2,0 are the roots of the given equation
Question 49:

Hence,  12 and 12 are the roots of the given equation
Question 50:

Hence, 3 and 2 are the roots of the given equation.

RS Aggarwal Solutions for Class 10 Maths Chapter 4: Download PDF

RS Aggarwal Solutions for Class 10 Maths Chapter 4–Quadratic Equations

Download PDF: RS Aggarwal Solutions for Class 10 Maths Chapter 4–Quadratic Equations PDF

Chapterwise RS Aggarwal Solutions for Class 10 Maths :

• Chapter 1–Real Numbers
• Chapter 2–Polynomials
• Chapter 3–Linear Equations In Two Variables
• Chapter 4–Quadratic Equations
• Chapter 5–Arithmetic Progression
• Chapter 6–Coordinate Geometry
• Chapter 7–Triangles
• Chapter 8–Circles
• Chapter 9–Constructions
• Chapter 10–Trigonometric Ratios
• Chapter 11–T Ratios Of Some Particular Angles
• Chapter 12–Trigonometric Ratios Of Some Complementary Angles
• Chapter 13–Trigonometric Identities
• Chapter 14–Height and Distance
• Chapter 15–Perimeter and Areas of Plane Figures
• Chapter 16–Areas of Circle, Sector and Segment
• Chapter 17–Volume and Surface Areas of Solids
• Chapter 18–Mean, Median, Mode of Grouped Data
• Chapter 19–Probability

About RS Aggarwal Class 10 Book

Investing in an R.S. Aggarwal book will never be of waste since you can use the book to prepare for various competitive exams as well. RS Aggarwal is one of the most prominent books with an endless number of problems. R.S. Aggarwal’s book very neatly explains every derivation, formula, and question in a very consolidated manner. It has tonnes of examples, practice questions, and solutions even for the NCERT questions.

He was born on January 2, 1946 in a village of Delhi. He graduated from Kirori Mal College, University of Delhi. After completing his M.Sc. in Mathematics in 1969, he joined N.A.S. College, Meerut, as a lecturer. In 1976, he was awarded a fellowship for 3 years and joined the University of Delhi for his Ph.D. Thereafter, he was promoted as a reader in N.A.S. College, Meerut. In 1999, he joined M.M.H. College, Ghaziabad, as a reader and took voluntary retirement in 2003. He has authored more than 75 titles ranging from Nursery to M. Sc. He has also written books for competitive examinations right from the clerical grade to the I.A.S. level.

FAQs

Why must I refer to the RS Aggarwal textbook?
RS Aggarwal is one of the most important reference books for high school grades and is recommended to every high school student. The book covers every single topic in detail. It goes in-depth and covers every single aspect of all the mathematics topics and covers both theory and problem-solving. The book is true of great help for every high school student. Solving a majority of the questions from the book can help a lot in understanding topics in detail and in a manner that is very simple to understand. Hence, as a high school student, you must definitely dwell your hands on RS Aggarwal!

Why should you refer to RS Aggarwal textbook solutions on Indcareer?
RS Aggarwal is a book that contains a few of the hardest questions of high school mathematics. Solving them and teaching students how to solve questions of such high difficulty is not the job of any neophyte. For solving such difficult questions and more importantly, teaching the problem-solving methodology to students, an expert teacher is mandatory!

Does IndCareer cover RS Aggarwal Textbook solutions for Class 6-12?
RS Aggarwal is available for grades 6 to 12 and hence our expert teachers have formulated detailed solutions for all the questions of each edition of the textbook. On our website, you’ll be able to find solutions to the RS Aggarwal textbook right from Class 6 to Class 12. You can head to the website and download these solutions for free. All the solutions are available in PDF format and are free to download!

Read More

• RS Aggarwal Solutions for Class 10 Maths Chapter 2–Polynomials
• RD Sharma Solutions for Class 10 Maths Chapter 8–Quadratic Equations
• RS Aggarwal Solutions for Class 10 Maths Chapter 1–Real Numbers
• CL Aggarwal DAV Model School
• NCERT Solutions for 4th Class Environmental Studies Chapter 19-Abdul In The Garden