RD Sharma Solutions for Class 12 Maths Chapter 5–Algebra of Matrices

Class 12: Maths Chapter 5 solutions. Complete Class 12 Maths Chapter 5 Notes.

RD Sharma Solutions for Class 12 Maths Chapter 5–Algebra of Matrices

RD Sharma 12th Maths Chapter 5, Class 12 Maths Chapter 5 solutions

Exercise 5.1 Page No: 5.6

1. If a matrix has 8 elements, what are the possible orders it can have? What if it has 5 elements?

Solution:

If a matrix is of order m × n elements, it has m n elements. So, if the matrix has 8 elements, we will find the ordered pairs m and n.

m n = 8

Then, ordered pairs m and n will be

m × n be (8 × 1),(1 × 8),(4 × 2),(2 × 4)

Now, if it has 5 elements

Possible orders are (5 × 1), (1 × 5).

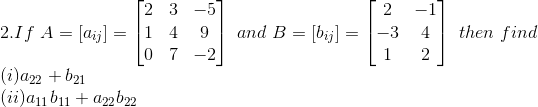
Solution:

(i)

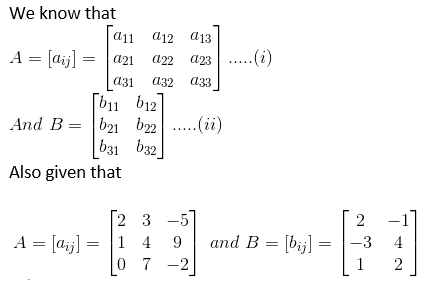
Now, Comparing with equation (1) and (2)

a₂₂ = 4 and b₂₁ = – 3

a₂₂ + b₂₁ = 4 + (– 3) = 1

(ii)

Now, Comparing with equation (1) and (2)

a₁₁ = 2, a₂₂ = 4, b₁₁ = 2, b₂₂ = 4

a₁₁ b₁₁ + a₂₂ b₂₂ = 2 × 2 + 4 × 4 = 4 + 16 = 20

3. Let A be a matrix of order 3 × 4. If R₁ denotes the first row of A and C₂ denotes its second column, then determine the orders of matrices R₁ and C₂.

Solution:

Given A be a matrix of order 3 × 4.

So, A = [a_{i j}] _3×4

R₁ = first row of A = [a₁₁, a₁₂, a₁₃, a₁₄]

So, order of matrix R₁ = 1 × 4

C₂ = second column of

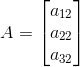
Therefore order of C₂ = 3 × 1

4. Construct a 2 ×3 matrix A = [a_{j j}] whose elements a_{j j} are given by:

(i) a_{i j} = i × j

(ii) a_{i j} = 2i – j

(iii) a_{i j} = i + j

(iv) a_{i j} = (i + j)²/2

Solution:

(i) Given a_{i j} = i × j

Let A = [a_{i j}]_{2 × 3}

So, the elements in a 2 × 3 matrix are[a₁₁, a₁₂, a₁₃, a₂₁, a₂₂, a₂₃]

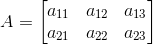
a₁₁ = 1 × 1 = 1

a₁₂ = 1 × 2 = 2

a₁₃ = 1 × 3 = 3

a₂₁ = 2 × 1 = 2

a₂₂ = 2 × 2 = 4

a₂₃ = 2 × 3 = 6

Substituting these values in matrix A we get,

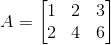
(ii) Given a_{i j} = 2i – j

Let A = [a_{i j}]_2×3

So, the elements in a 2 × 3 matrix are

a₁₁, a₁₂, a₁₃, a₂₁, a₂₂, a₂₃

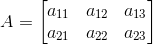
a₁₁ = 2 × 1 – 1 = 2 – 1 = 1

a₁₂ = 2 × 1 – 2 = 2 – 2 = 0

a₁₃ = 2 × 1 – 3 = 2 – 3 = – 1

a₂₁ = 2 × 2 – 1 = 4 – 1 = 3

a₂₂ = 2 × 2 – 2 = 4 – 2 = 2

a₂₃ = 2 × 2 – 3 = 4 – 3 = 1

Substituting these values in matrix A we get,

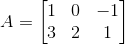
(iii) Given a_{i j} = i + j

Let A = [a _{i j}] _2×3

So, the elements in a 2 × 3 matrix are

a₁₁, a₁₂, a₁₃, a₂₁, a₂₂, a₂₃

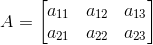
a₁₁ = 1 + 1 = 2

a₁₂ = 1 + 2 = 3

a₁₃ = 1 + 3 = 4

a₂₁ = 2 + 1 = 3

a₂₂ = 2 + 2 = 4

a₂₃ = 2 + 3 = 5

Substituting these values in matrix A we get,

(iv) Given a_{i j} = (i + j)²/2

Let A = [a_{i j}]_2×3

So, the elements in a 2 × 3 matrix are

a₁₁, a₁₂, a₁₃, a₂₁, a₂₂, a₂₃

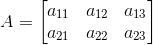
Let A = [a_{i j}]_2×3

So, the elements in a 2 × 3 matrix are

a₁₁, a₁₂, a₁₃, a₂₁, a₂₂, a₂₃

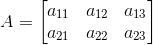
a₁₁ =

a₁₂ =

a₁₃ =

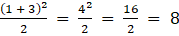
a₂₁ =

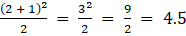
a₂₂ =

a₂₃ =

Substituting these values in matrix A we get,

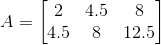
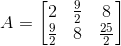
5. Construct a 2 × 2 matrix A = [a_{i j}] whose elements a_{i j} are given by:

(i) (i + j)² /2

(ii) a_{i j} = (i – j)² /2

(iii) a_{i j} = (i – 2j)² /2

(iv) a_{i j} = (2i + j)² /2

(v) a_{i j} = |2i – 3j|/2

(vi) a_{i j} = |-3i + j|/2

(vii) a_{i j} = e^2ix sin x j

Solution:

(i) Given (i + j)² /2

Let A = [a_{i j}]_2×2

So, the elements in a 2 × 2 matrix are

a₁₁, a₁₂, a₂₁, a₂₂

a₁₁ =

a₁₂ =

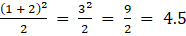
a₂₁ =

a₂₂ =

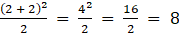
Substituting these values in matrix A we get,

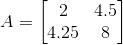
(ii) Given a_{i j} = (i – j)² /2

Let A = [a_{i j}]_2×2

So, the elements in a 2 × 2 matrix are

a₁₁, a₁₂, a₂₁, a₂₂

a₁₁ =

a₁₂ =

a₂₁ =

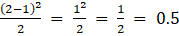
a₂₂ =

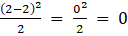
Substituting these values in matrix A we get,

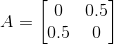
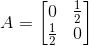
(iii) Given a_{i j} = (i – 2j)² /2

Let A = [a_{i j}]_2×2

So, the elements in a 2 × 2 matrix are

a₁₁, a₁₂, a₂₁, a₂₂

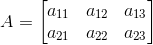
a₁₁ =

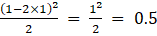
a₁₂ =

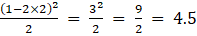
a₂₁ =

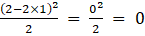
a₂₂ =

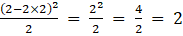
Substituting these values in matrix A we get,

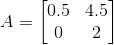
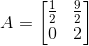
(iv) Given a_{i j} = (2i + j)² /2

Let A = [a_{i j}]_2×2

So, the elements in a 2 × 2 matrix are

a₁₁, a₁₂, a₂₁, a₂₂

a₁₁ =

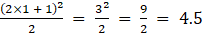
a₁₂ =

a₂₁ =

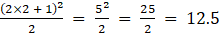
a₂₂ =

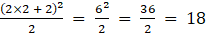
Substituting these values in matrix A we get,

(v) Given a_{i j} = |2i – 3j|/2

Let A = [a_{i j}]_2×2

So, the elements in a 2×2 matrix are

a₁₁, a₁₂, a₂₁, a₂₂

a₁₁ =

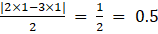
a₁₂ =

a₂₁ =

a₂₂ =

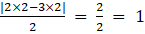
Substituting these values in matrix A we get,

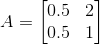
(vi) Given a_{i j} = |-3i + j|/2

Let A = [a_{i j}]_2×2

So, the elements in a 2 × 2 matrix are

a₁₁, a₁₂, a₂₁, a₂₂

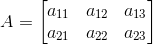
a₁₁ =

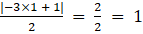
a₁₂ =

a₂₁ =

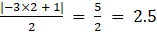
a₂₂ =

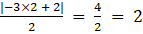
Substituting these values in matrix A we get,

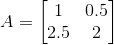
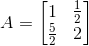
(vii) Given a_{i j} = e^2ix sin x j

Let A = [a_{i j}]_2×2

So, the elements in a 2 × 2 matrix are

a₁₁, a₁₂, a₂₁, a₂₂,

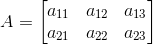
a₁₁ =

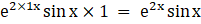
a₁₂ =

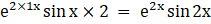
a₂₁ =

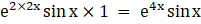
a₂₂ =

Substituting these values in matrix A we get,

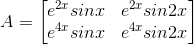
6. Construct a 3×4 matrix A = [a_{i j}] whose elements a_{i j} are given by:
(i) a_{i j} = i + j

(ii) a_{i j} = i – j

(iii) a_{i j} = 2i

(iv) a_{i j} = j

(v) a_{i j} = ½ |-3i + j|

Solution:

(i) Given a_{i j} = i + j

Let A = [a_{i j}]_2×3

So, the elements in a 3 × 4 matrix are

a₁₁, a₁₂, a₁₃, a_14, a₂₁, a₂₂, a₂₃, a₂₄, a_31, a_32, a_33, a₃₄

A =

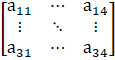
a₁₁ = 1 + 1 = 2

a₁₂ = 1 + 2 = 3

a₁₃ = 1 + 3 = 4

a₁₄ = 1 + 4 = 5

a₂₁ = 2 + 1 = 3

a₂₂ = 2 + 2 = 4

a₂₃ = 2 + 3 = 5

a_{24 =} 2 + 4 = 6

a₃₁ = 3 + 1 = 4

a₃₂ = 3 + 2 = 5

a₃₃ = 3 + 3 = 6

a₃₄ = 3 + 4 = 7

Substituting these values in matrix A we get,

A =

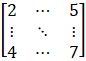
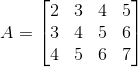
(ii) Given a_{i j} = i – j

Let A = [a_{i j}]_2×3

So, the elements in a 3×4 matrix are

a₁₁, a₁₂, a₁₃, a_14, a₂₁, a₂₂, a₂₃, a₂₄, a_31, a_32, a_33, a₃₄

A =

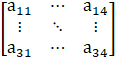
a₁₁ = 1 – 1 = 0

a₁₂ = 1 – 2 = – 1

a₁₃ = 1 – 3 = – 2

a₁₄ = 1 – 4 = – 3

a₂₁ = 2 – 1 = 1

a₂₂ = 2 – 2 = 0

a₂₃ = 2 – 3 = – 1

a_{24 =} 2 – 4 = – 2

a₃₁ = 3 – 1 = 2

a₃₂ = 3 – 2 = 1

a₃₃ = 3 – 3 = 0

a₃₄ = 3 – 4 = – 1

Substituting these values in matrix A we get,

A =

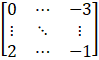
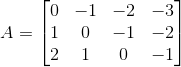
(iii) Given a_{i j} = 2i

Let A = [a_{i j}]_2×3

So, the elements in a 3×4 matrix are

a₁₁, a₁₂, a₁₃, a_14, a₂₁, a₂₂, a₂₃, a₂₄, a_31, a_32, a_33, a₃₄

A =

a₁₁ = 2×1 = 2

a₁₂ = 2×1 = 2

a₁₃ = 2×1 = 2

a₁₄ = 2×1 = 2

a₂₁ = 2×2 = 4

a₂₂ = 2×2 = 4

a₂₃ = 2×2 = 4

a_{24 =} 2×2 = 4

a₃₁ = 2×3 = 6

a₃₂ = 2×3 = 6

a₃₃ = 2×3 = 6

a₃₄ = 2×3 = 6

Substituting these values in matrix A we get,

A =

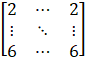
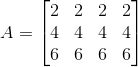
(iv) Given a_{i j} = j

Let A = [a_{i j}]_2×3

So, the elements in a 3×4 matrix are

a₁₁, a₁₂, a₁₃, a_14, a₂₁, a₂₂, a₂₃, a₂₄, a_31, a_32, a_33, a₃₄

A =

a₁₁ = 1

a₁₂ = 2

a₁₃ = 3

a₁₄ = 4

a₂₁ = 1

a₂₂ = 2

a₂₃ = 3

a_{24 =} 4

a₃₁ = 1

a₃₂ = 2

a₃₃ = 3

a₃₄ = 4

Substituting these values in matrix A we get,

A =

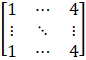
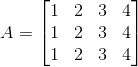
(vi) Given a_{i j} = ½ |-3i + j|

Let A = [a_{i j}]_2×3

So, the elements in a 3×4 matrix are

a₁₁, a₁₂, a₁₃, a_14, a₂₁, a₂₂, a₂₃, a₂₄, a_31, a_32, a_33, a₃₄

A =

a₁₁ =

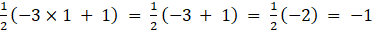
a₁₂ =

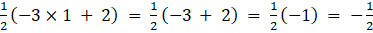
a₁₃ =

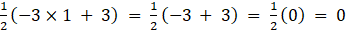
a₁₄ =

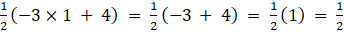
a₂₁ =

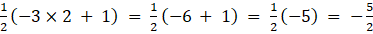
a₂₂ =

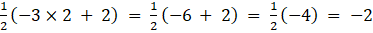
a₂₃ =

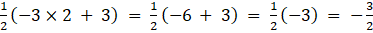
a_{24 =}

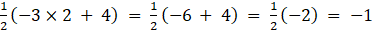
a₃₁ =

a₃₂ =

a₃₃ =

a₃₄ =

Substituting these values in matrix A we get,

A =

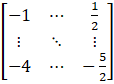
Multiplying by negative sign we get,

7. Construct a 4 × 3 matrix A = [a_{i j}] whose elements a_{i j} are given by:

(i) a_{i j} = 2i + i/j

(ii) a_{i j} = (i – j)/ (i + j)

(iii) a_{i j} = i

Solution:

(i) Given a_{i j} = 2i + i/j

Let A = [a_{i j}]_4×3

So, the elements in a 4 × 3 matrix are

a₁₁, a₁₂, a₁₃, a₂₁, a₂₂, a₂₃, a_31, a_32, a_33, a_41, a_42, a₄₃

A =

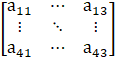
a₁₁ =

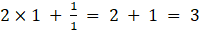
a₁₂ =

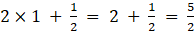
a₁₃ =

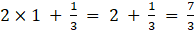
a₂₁ =

a₂₂ =

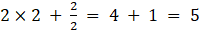
a₂₃ =

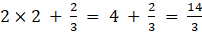
a₃₁ =

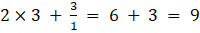
a₃₂ =

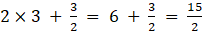
a₃₃ =

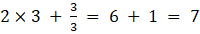
a₄₁ =

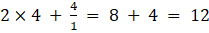
a₄₂ =

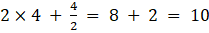
a₄₃ =

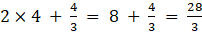
Substituting these values in matrix A we get,

A =

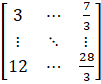
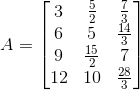
(ii) Given a_{i j} = (i – j)/ (i + j)

Let A = [a_{i j}]_4×3

So, the elements in a 4 × 3 matrix are

a₁₁, a₁₂, a₁₃, a₂₁, a₂₂, a₂₃, a_31, a_32, a_33, a_41, a_42, a₄₃

A =

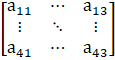
a₁₁ =

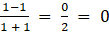
a₁₂ =

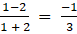
a₁₃ =

a₂₁ =

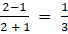
a₂₂ =

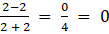
a₂₃ =

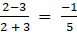
a₃₁ =

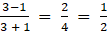
a₃₂ =

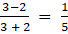
a₃₃ =

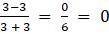
a₄₁ =

a₄₂ =

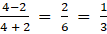
a₄₃ =

Substituting these values in matrix A we get,

A =

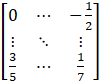
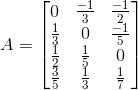
(iii) Given a_{i j} = i

Let A = [a_{i j}]_4×3

So, the elements in a 4 × 3 matrix are

a₁₁, a₁₂, a₁₃, a₂₁, a₂₂, a₂₃, a_31, a_32, a_33, a_41, a_42, a₄₃

A =

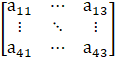
a₁₁ = 1

a₁₂ = 1

a₁₃ = 1

a₂₁ = 2

a₂₂ = 2

a₂₃ = 2

a₃₁ = 3

a₃₂ = 3

a₃₃ = 3

a₄₁ = 4

a₄₂ = 4

a₄₃ = 4

Substituting these values in matrix A we get,

A =

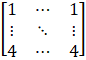
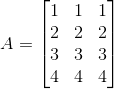
8. Find x, y, a and b if

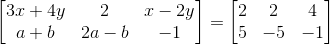
Solution:

Given

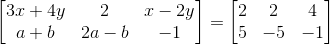
Given that two matrices are equal.

We know that if two matrices are equal then the elements of each matrices are also equal.

Therefore by equating them we get,

3x + 4y = 2 …… (1)

x – 2y = 4 …… (2)

a + b = 5 …… (3)

2a – b = – 5 …… (4)

Multiplying equation (2) by 2 and adding to equation (1), we get

3x + 4y + 2x – 4y = 2 + 8

⇒ 5x = 10

⇒ x = 2

Now, substituting the value of x in equation (1)

3 × 2 + 4y = 2

⇒ 6 + 4y = 2

⇒ 4y = 2 – 6

⇒ 4y = – 4

⇒ y = – 1

Now by adding equation (3) and (4)

a + b + 2a – b = 5 + (– 5)

⇒ 3a = 5 – 5 = 0

⇒ a = 0

Now, again by substituting the value of a in equation (3), we get

0 + b = 5

⇒ b = 5

∴ a = 0, b = 5, x = 2 and y = – 1

9. Find x, y, a and b if

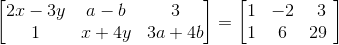
Solution:

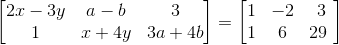
We know that if two matrices are equal then the elements of each matrices are also equal.

Given that two matrices are equal.

Therefore by equating them we get,

2a + b = 4 …… (1)

And a – 2b = – 3 …… (2)

And 5c – d = 11 …… (3)

4c + 3d = 24 …… (4)

Multiplying equation (1) by 2 and adding to equation (2)

4a + 2b + a – 2b = 8 – 3

⇒ 5a = 5

⇒ a = 1

Now, substituting the value of a in equation (1)

2 × 1 + b = 4

⇒ 2 + b = 4

⇒ b = 4 – 2

⇒ b = 2

Multiplying equation (3) by 3 and adding to equation (4)

15c – 3d + 4c + 3d = 33 + 24

⇒ 19c = 57

⇒ c = 3

Now, substituting the value of c in equation (4)

4 × 3 + 3d = 24

⇒ 12 + 3d = 24

⇒ 3d = 24 – 12

⇒ 3d = 12

⇒ d = 4

∴ a = 1, b = 2, c = 3 and d = 4

10. Find the values of a, b, c and d from the following equations:

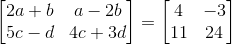
Solution:

Given

We know that if two matrices are equal then the elements of each matrices are also equal.

Given that two matrices are equal.

Therefore by equating them we get,

2a + b = 4 …… (1)

And a – 2b = – 3 …… (2)

And 5c – d = 11 …… (3)

4c + 3d = 24 …… (4)

Multiplying equation (1) by 2 and adding to equation (2)

4a + 2b + a – 2b = 8 – 3

⇒ 5a = 5

⇒ a = 1

Now, substituting the value of a in equation (1)

2 × 1 + b = 4

⇒ 2 + b = 4

⇒ b = 4 – 2

⇒ b = 2

Multiplying equation (3) by 3 and adding to equation (4)

15c – 3d + 4c + 3d = 33 + 24

⇒ 19c = 57

⇒ c = 3

Now, substituting the value of c in equation (4)

4 × 3 + 3d = 24

⇒ 12 + 3d = 24

⇒ 3d = 24 – 12

⇒ 3d = 12

⇒ d = 4

∴ a = 1, b = 2, c = 3 and d = 4

Exercise 5.2 Page No: 5.18

1. Compute the following sums:

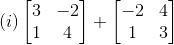
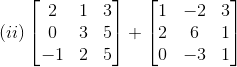
Solution:

(i) Given

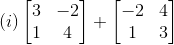
Corresponding elements of two matrices should be added

Therefore, we get

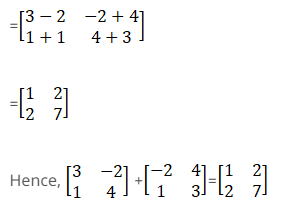
Therefore,

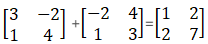
(ii) Given

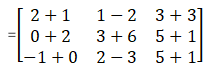
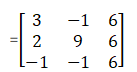
Therefore,

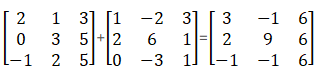
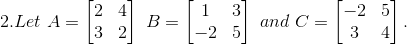
Find each of the following:

(i) 2A – 3B

(ii) B – 4C

(iii) 3A – C

(iv) 3A – 2B + 3C

Solution:

(i) Given

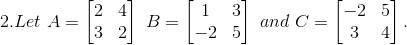
First we have to compute 2A

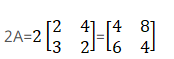
Now by computing 3B we get,

Now by we have to compute 2A – 3B we get

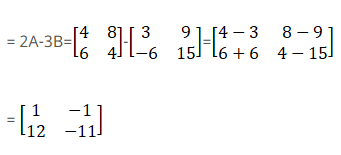
Therefore

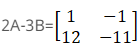
(ii) Given

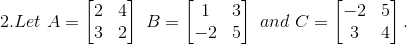
First we have to compute 4C,

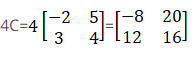
Now,

Therefore we get,

(iii) Given

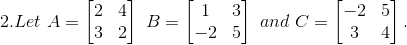
First we have to compute 3A,

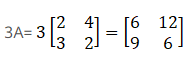
Now,

Therefore,

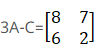
(iv) Given

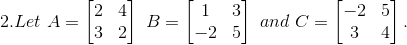
First we have to compute 3A

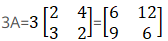
Now we have to compute 2B

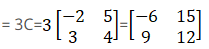
By computing 3C we get,

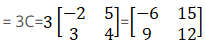
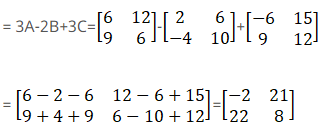
Therefore,

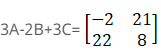
(i) A + B and B + C

(ii) 2B + 3A and 3C – 4B

Solution:

(i) Consider A + B,

A + B is not possible because matrix A is an order of 2 x 2 and Matrix B is an order of 2 x 3, so the Sum of the matrix is only possible when their order is same.

Now consider B + C

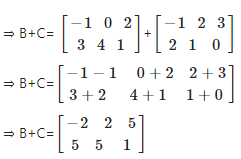
(ii) Consider 2B + 3A

2B + 3A also does not exist because the order of matrix B and matrix A is different, so we cannot find the sum of these matrix.

Now consider 3C – 4B,

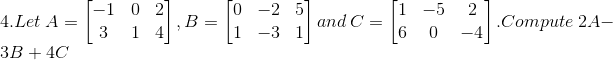
Solution:

Given

Now we have to compute 2A – 3B + 4C

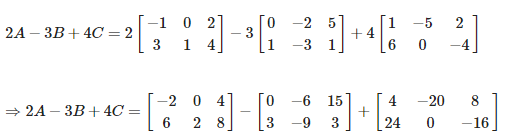
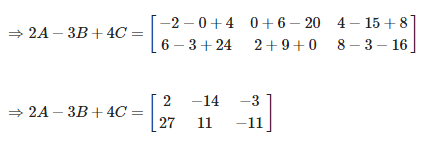
5. If A = diag (2 -5 9), B = diag (1 1 -4) and C = diag (-6 3 4), find

(i) A – 2B

(ii) B + C – 2A

(iii) 2A + 3B – 5C

Solution:

(i) Given A = diag (2 -5 9), B = diag (1 1 -4) and C = diag (-6 3 4)

(ii) Given A = diag (2 -5 9), B = diag (1 1 -4) and C = diag (-6 3 4)

We have to find B + C – 2A

Here,

Now we have to compute B + C – 2A

(iii) Given A = diag (2 -5 9), B = diag (1 1 -4) and C = diag (-6 3 4)

Now we have to find 2A + 3B – 5C

Here,

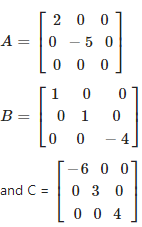
Now consider 2A + 3B – 5C

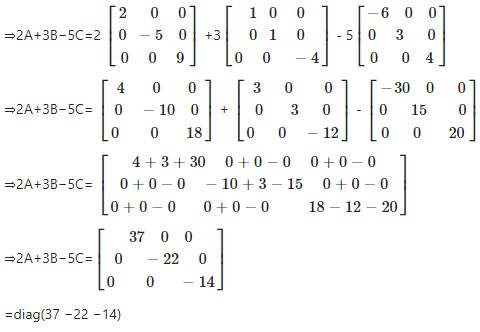
6. Given the matrices

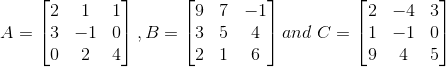
Verify that (A + B) + C = A + (B + C)

Solution:

Given

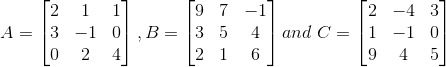
Now we have to verify (A + B) + C = A + (B + C)

First consider LHS, (A + B) + C,

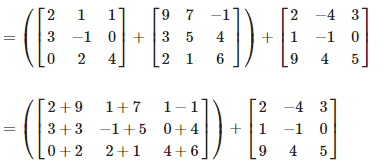
Now consider RHS, that is A + (B + C)

Therefore LHS = RHS

Hence (A + B) + C = A + (B + C)

7. Find the matrices X and Y,

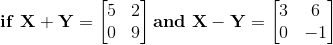
Solution:

Consider,

Now by simplifying we get,

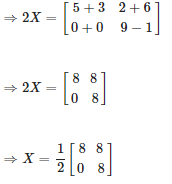
Therefore,

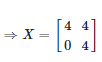
Again consider,

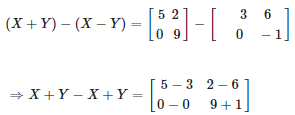
Now by simplifying we get,

Therefore,

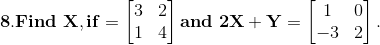
Solution:

Given

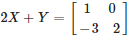
Now by transposing, we get

Therefore,

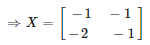
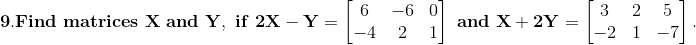
Solution:

Given

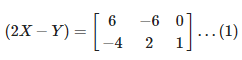
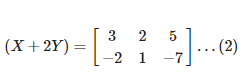
Now by multiplying equation (1) and (2) we get,

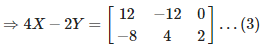
Now by adding equation (2) and (3) we get,

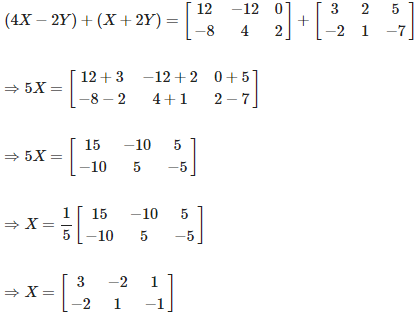
Now by substituting X in equation (2) we get,

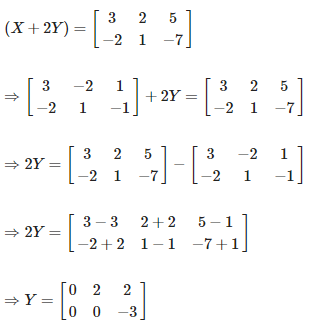
Solution:

Consider

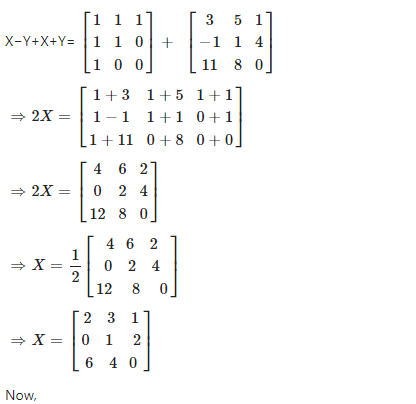
Now, again consider

Therefore,

And

Exercise 5.3 Page No: 5.41

1. Compute the indicated products:

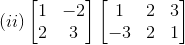
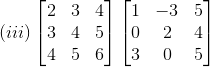
Solution:

(i) Consider

On simplification we get,

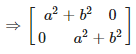
(ii) Consider

On simplification we get,

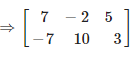
(iii) Consider

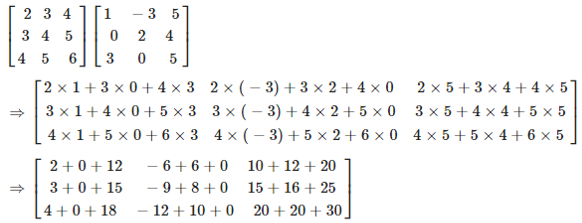
On simplification we get,

2. Show that AB ≠ BA in each of the following cases:

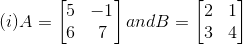
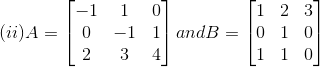
Solution:

(i) Consider,

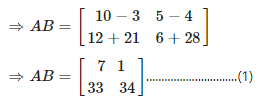
Again consider,

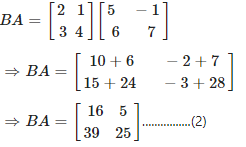
From equation (1) and (2), it is clear that

AB ≠ BA

(ii) Consider,

Now again consider,

From equation (1) and (2), it is clear that

AB ≠ BA

(iii) Consider,

Now again consider,

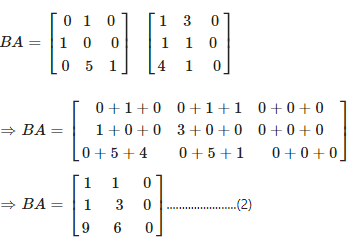
From equation (1) and (2), it is clear that

AB ≠ BA

3. Compute the products AB and BA whichever exists in each of the following cases:

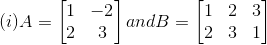
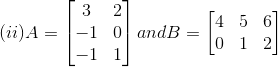
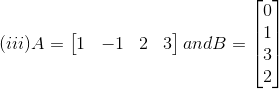
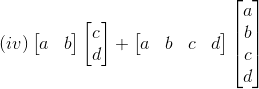
Solution:

(i) Consider,

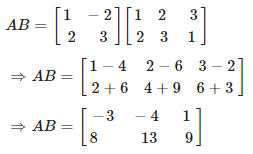
BA does not exist

Because the number of columns in B is greater than the rows in A

(ii) Consider,

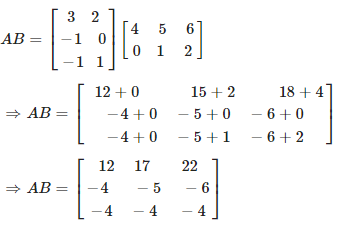
Again consider,

(iii) Consider,

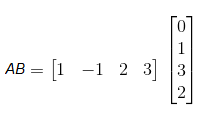
AB = [0 + (-1) + 6 + 6]

AB = 11

Again consider,

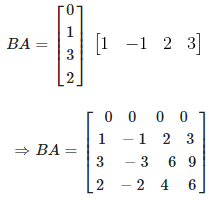
(iv) Consider,

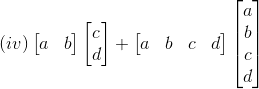
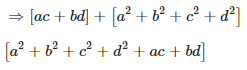
4. Show that AB ≠ BA in each of the following cases:

Solution:

(i) Consider,

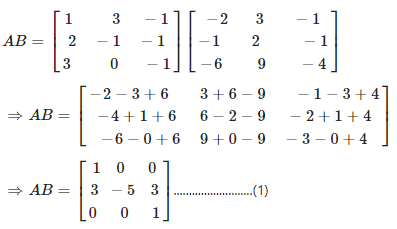
Again consider,

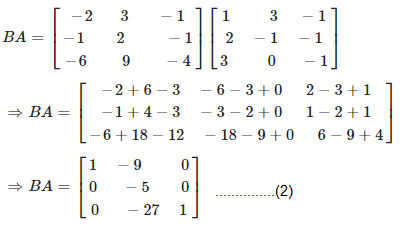
From equation (1) and (2), it is clear that

AB ≠ BA

(ii) Consider,

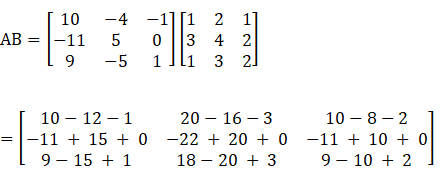
Again consider,

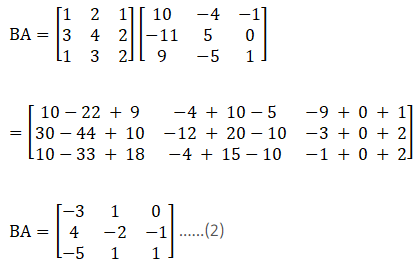
From equation (1) and (2) it is clear that,

AB ≠ BA

5. Evaluate the following:

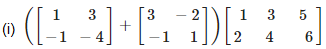
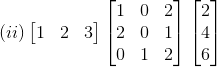
Solution:

(i) Given

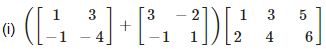
First we have to add first two matrix,

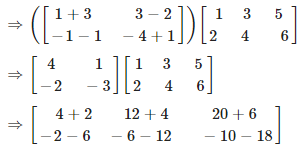
On simplifying, we get

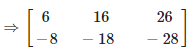
(ii) Given,

First we have to multiply first two given matrix,

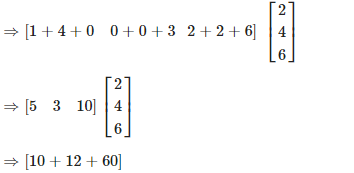
= 82

(iii) Given

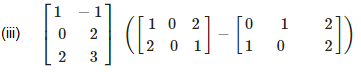
First we have subtract the matrix which is inside the bracket,

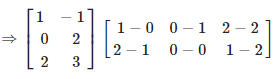
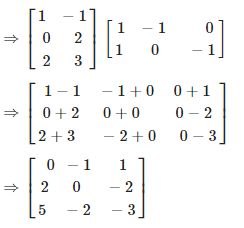
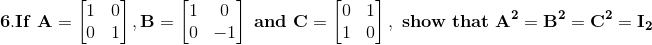
Solution:

Given

We know that,

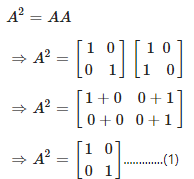
Again we know that,

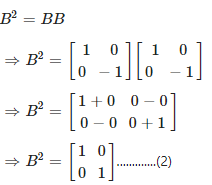
Now, consider,

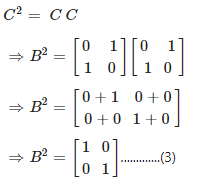
We have,

Now, from equation (1), (2), (3) and (4), it is clear that A² = B²= C²= I₂

Solution:

Given

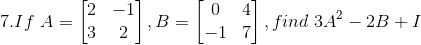
Consider,

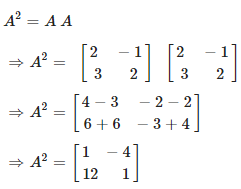
Now we have to find,

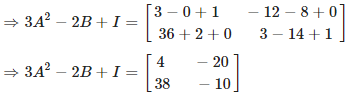
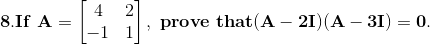
Solution:

Given

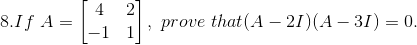
Consider,

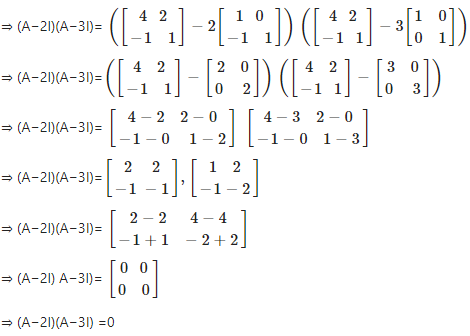
Hence the proof.

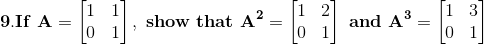
Solution:

Given,

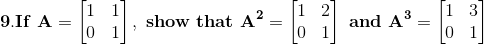
Consider,

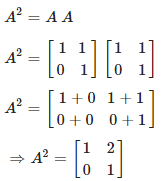
Again consider,

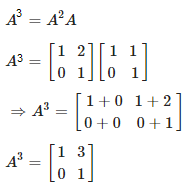
Hence the proof.

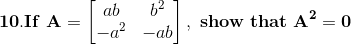
Solution:

Given,

Consider,

Hence the proof.

Solution:

Given,

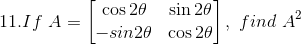
Consider,

We know that,

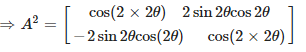
Again we have,

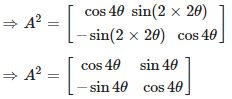
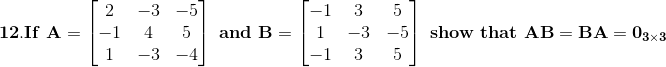
Solution:

Given,

Consider,

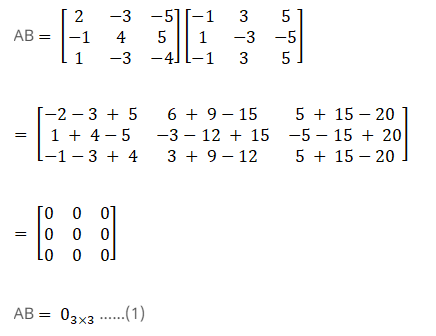
Again consider,

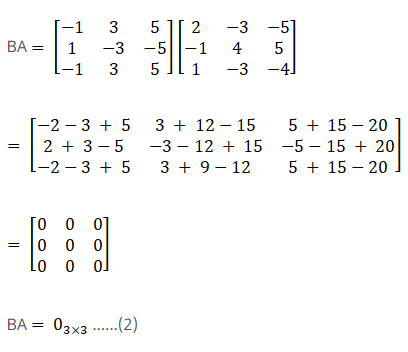
From equation (1) and (2) AB = BA = 0_3×3

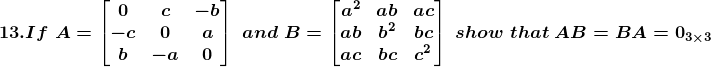
Solution:

Given

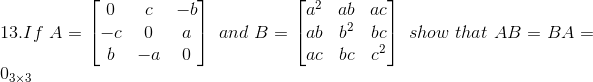
Consider,

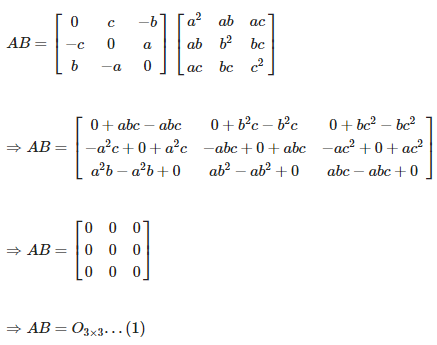
Again consider,

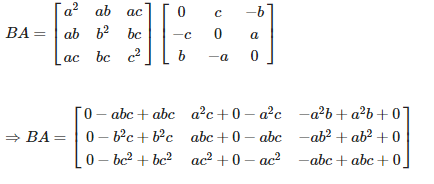
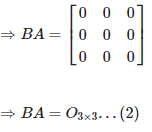
From equation (1) and (2) AB = BA = 0_3×3

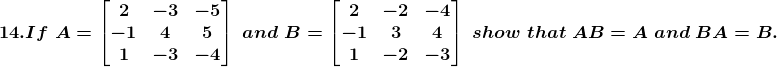
Solution:

Given

Now consider,

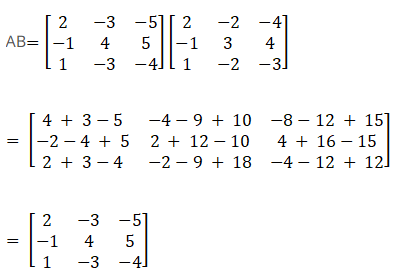
Therefore AB = A

Again consider, BA we get,

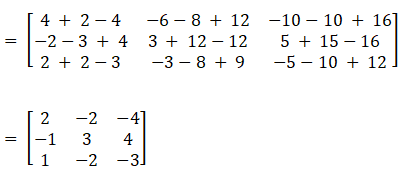
Hence BA = B

Hence the proof.

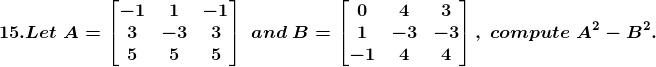
Solution:

Given,

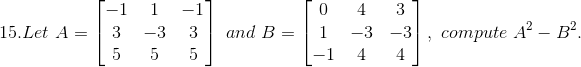
Consider,

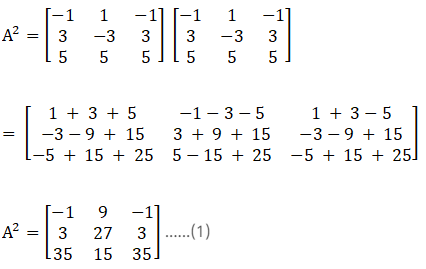
Now again consider, B²

Now by subtracting equation (2) from equation (1) we get,

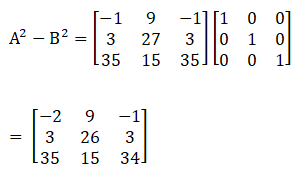
16. For the following matrices verify the associativity of matrix multiplication i.e. (AB) C = A (BC)

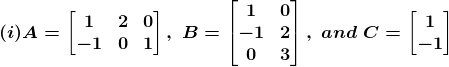
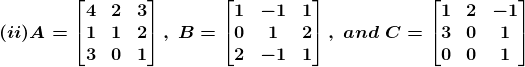
Solution:

(i) Given

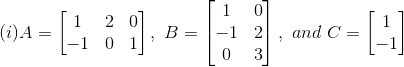
Consider,

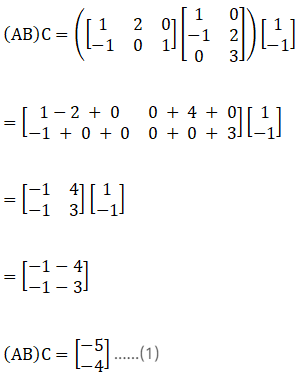
Now consider RHS,

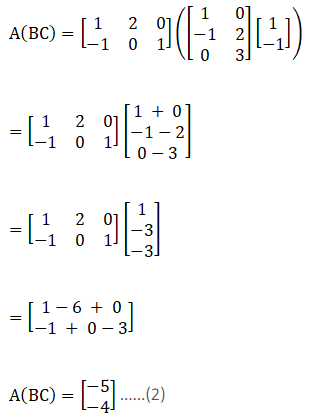
From equation (1) and (2), it is clear that (AB) C = A (BC)

(ii) Given,

Consider the LHS,

Now consider RHS,

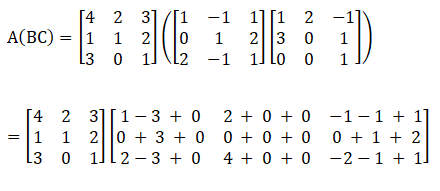
From equation (1) and (2), it is clear that (AB) C = A (BC)

17. For the following matrices verify the distributivity of matrix multiplication over matrix addition i.e. A (B + C) = AB + AC.

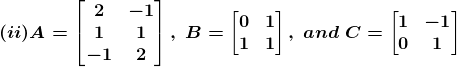
Solution:

(i) Given

Consider LHS,

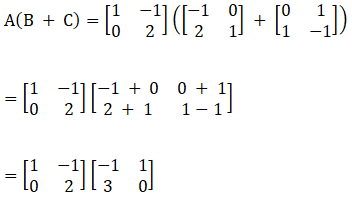
Now consider RHS,

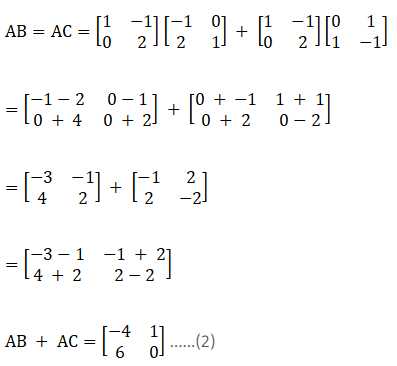
From equation (1) and (2), it is clear that A (B + C) = AB + AC

(ii) Given,

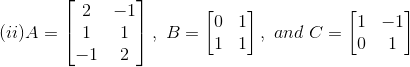
Consider the LHS

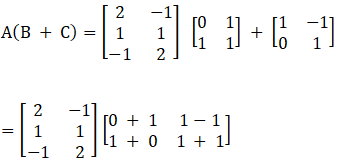
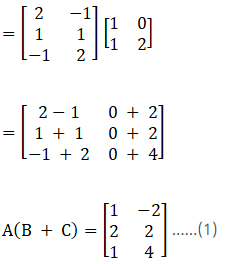
Now consider RHS,

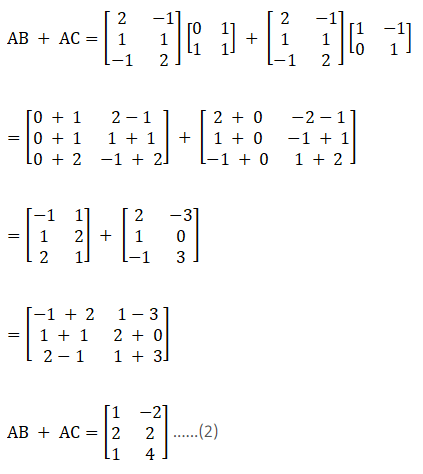
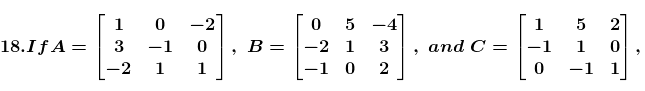
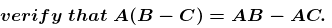
Solution:

Given,

Consider the LHS,

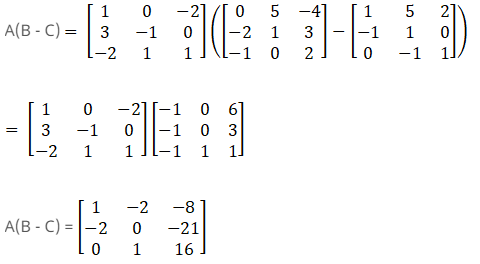
Now consider RHS

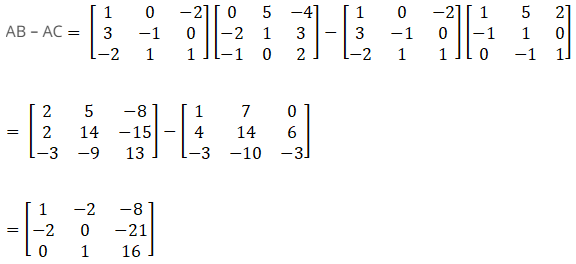
From the above equations LHS = RHS

Therefore, A (B – C) = AB – AC.

19. Compute the elements a₄₃ and a₂₂ of the matrix:

Solution:

Given

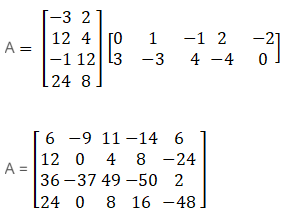
From the above matrix, a₄₃ = 8and a₂₂ = 0

Solution:

Given

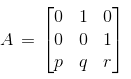
Consider,

Again consider,

Now, consider the RHS

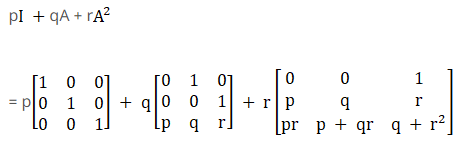
Therefore, A³ = p I + q A + rA²

Hence the proof.

21. If ω is a complex cube root of unity, show that

Solution:

Given

It is also given that ω is a complex cube root of unity,

Consider the LHS,

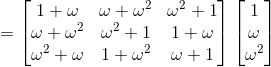
We know that 1 + ω + ω² = 0 and ω³ = 1

Now by simplifying we get,

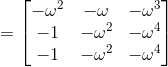
Again by substituting 1 + ω + ω² = 0 and ω³ = 1 in above matrix we get,

Therefore LHS = RHS

Hence the proof.

Solution:

Given,

Consider A²

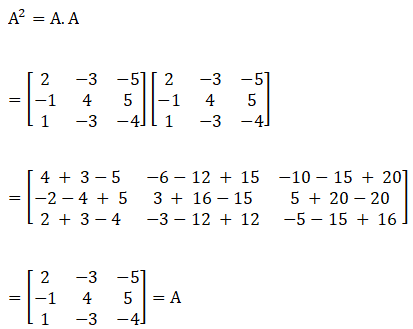
Therefore A² = A

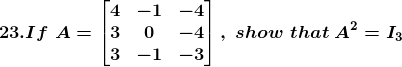
Solution:

Given

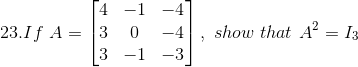
Consider A²,

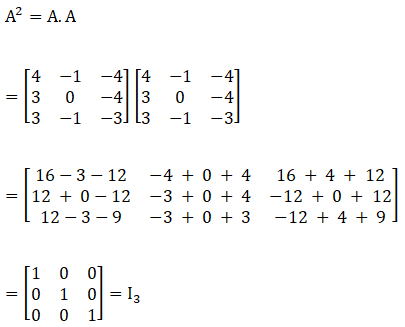
Hence A² = I₃

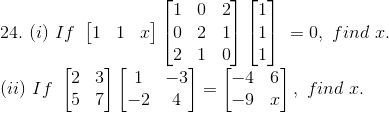
Solution:

(i) Given

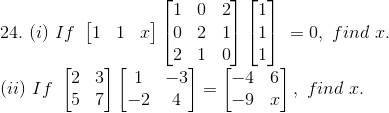
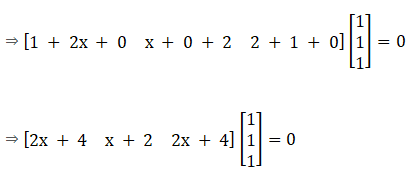
= [2x + 1 + 2 + x + 3] = 0

= [3x + 6] = 0

= 3x = -6

x = -6/3

x = -2

(ii) Given,

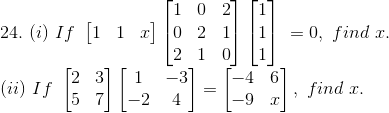
On comparing the above matrix we get,

x = 13

Solution:

Given

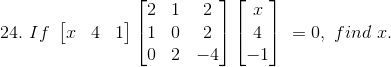
⇒ [(2x + 4) x + 4 (x + 2) – 1(2x + 4)] = 0

⇒ 2x² + 4x + 4x + 8 – 2x – 4 = 0

⇒ 2x² + 6x + 4 = 0

⇒ 2x² + 2x + 4x + 4 = 0

⇒ 2x (x + 1) + 4 (x + 1) = 0

⇒ (x + 1) (2x + 4) = 0

⇒ x = -1 or x = -2

Hence, x = -1 or x = -2

Solution:

Given

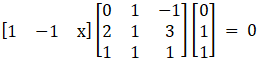
By multiplying we get,

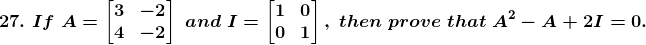
Solution:

Given

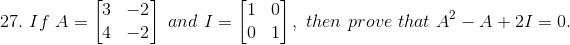
Now we have to prove A² – A + 2 I = 0

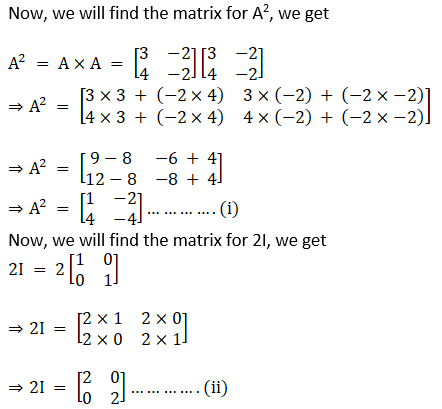
Solution:

Given

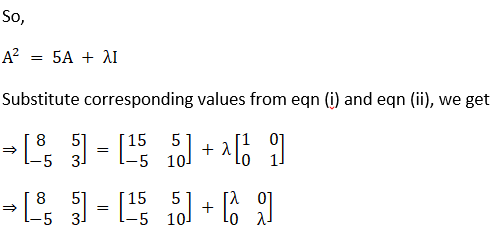
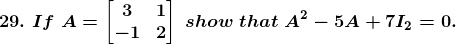
Solution:

Given

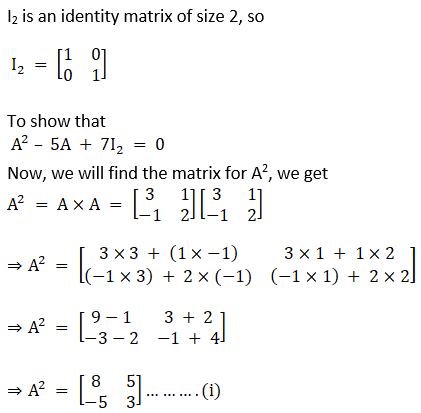
Hence the proof.

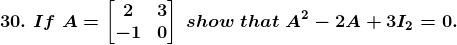
Solution:

Given

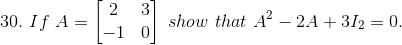
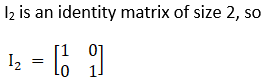
Hence the proof.

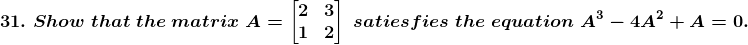
Solution:

Given

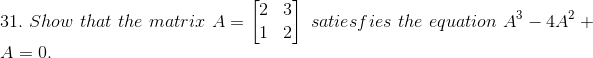
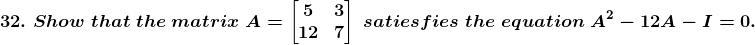
Solution:

Given

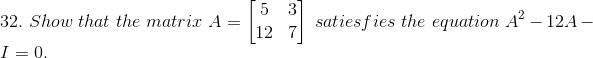
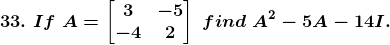
Solution:

Given

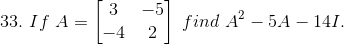
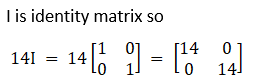
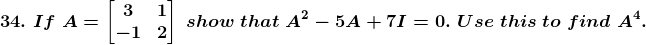
Solution:

Given

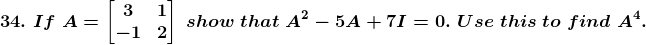
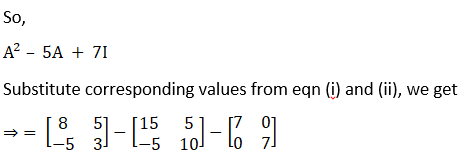
Solution:

Given

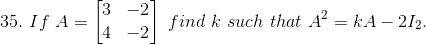
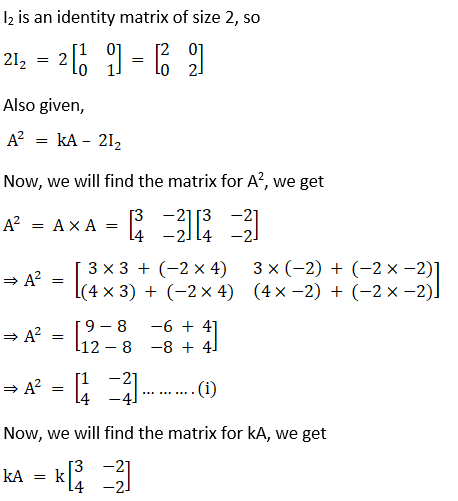
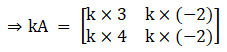
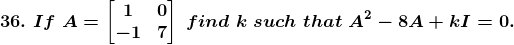
Solution:

Given

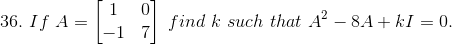
I is identity matrix, so

Also given,

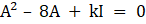
Now, we have to find A², we get

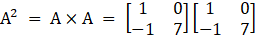
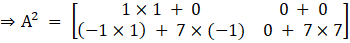
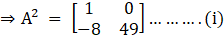
Now, we will find the matrix for 8A, we get

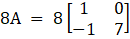
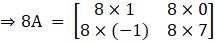
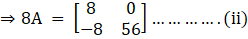
So,

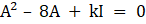
Substitute corresponding values from eqn (i) and (ii), we get

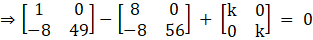
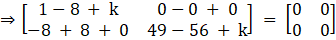
And to satisfy the above condition of equality, the corresponding entries of the matrices should be equal

Hence,

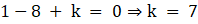
Therefore, the value of k is 7

Solution:

Given

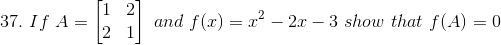
To show that f (A) = 0

Substitute x = A in f(x), we get

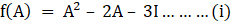
I is identity matrix, so

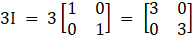
Now, we will find the matrix for A², we get

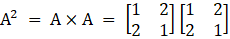
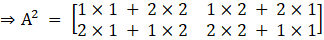
Now, we will find the matrix for 2A, we get

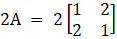
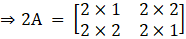
Substitute corresponding values from eqn (ii) and (iii) in eqn (i), we get

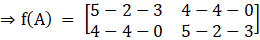
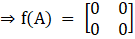
So,

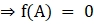
Hence Proved

Solution:

Given

So

Now, we will find the matrix for A², we get

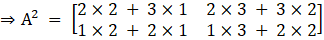
Now, we will find the matrix for λ A, we get

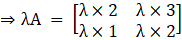
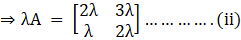
But given, A² = λ A + μ I

Substitute corresponding values from equation (i) and (ii), we get

And to satisfy the above condition of equality, the corresponding entries of the matrices should be equal

Hence, λ + 0 = 4 ⇒ λ = 4

And also, 2λ + μ = 7

Substituting the obtained value of λ in the above equation, we get

2(4) + μ = 7 ⇒ 8 + μ = 7 ⇒ μ = – 1

Therefore, the value of λ and μ are 4 and – 1 respectively

39. Find the value of x for which the matrix product

Solution:

We know,

is identity matrix of size 3.

So according to the given criteria

Now we will multiply the two matrices on LHS using the formula c_ij = a_i1b_1j + a_i2b_2j + … + a_in b_nj, we get

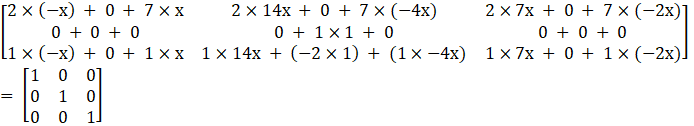
And to satisfy the above condition of equality, the corresponding entries of the matrices should be equal

So we get

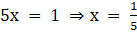
So the value of x is

Exercise 5.4 Page No: 5.54

(i) (2A)^T = 2 A^T

(ii) (A + B)^T = A^T + B^T

(iii) (A – B)^T = A^T – B^T

(iv) (AB)^T = B^T A^T

Solution:

(i) Given

Consider,

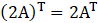
Put the value of A

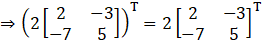
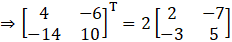
L.H.S = R.H.S

(ii) Given

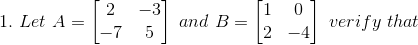
Consider,

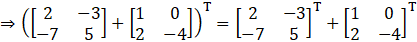
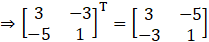
L.H.S = R.H.S

Hence proved.

(iii) Given

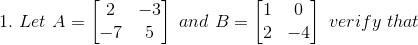
Consider,

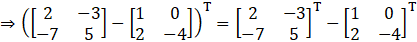
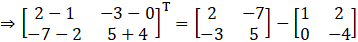
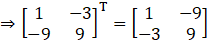
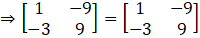
L.H.S = R.H.S

(iv) Given

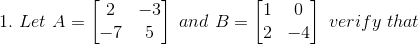
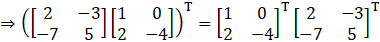
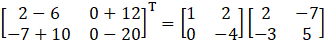
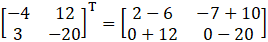
So,

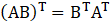
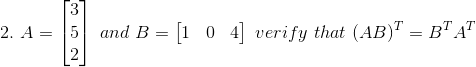
Solution:

Given

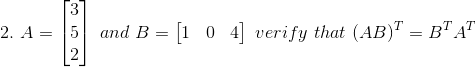
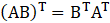
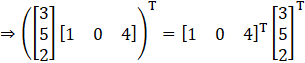
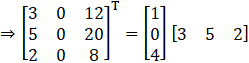
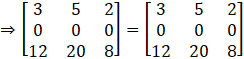
L.H.S = R.H.S

So,

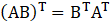
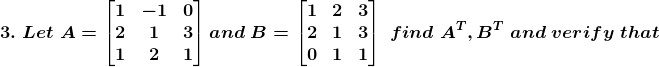
(i) A + B)^T = A^T + B^T

(ii) (AB)^T = B^T A^T

(iii) (2A)^T = 2 A^T

Solution:

(i) Given

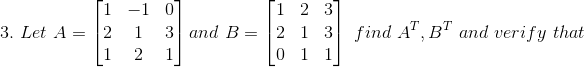
Consider,

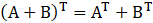
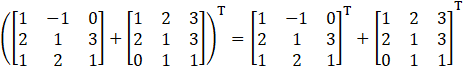
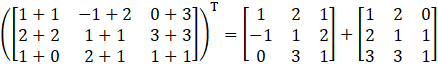
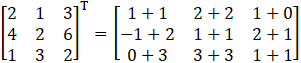
L.H.S = R.H.S

So,

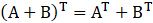
(ii) Given

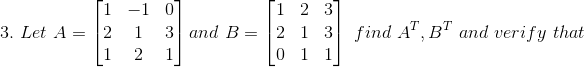
Consider,

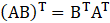
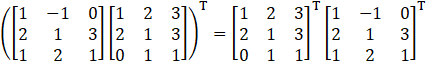
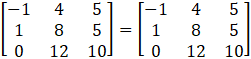
L.H.S = R.H.S

So,

(iii) Given

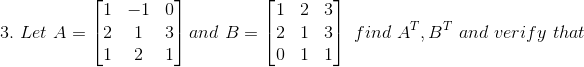
Consider,

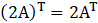
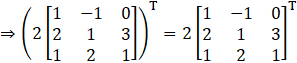
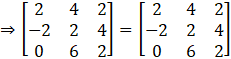
L.H.S = R.H.S

So,

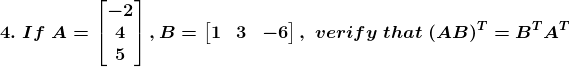
Solution:

Given

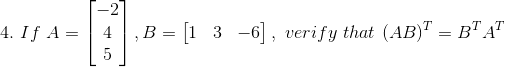
Consider,

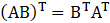
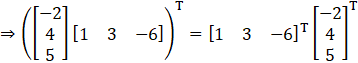
L.H.S = R.H.S

So,

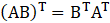
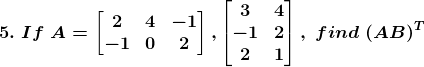
Solution:

Given

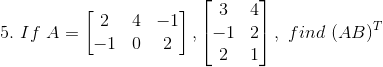
Now we have to find (AB)^T

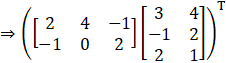
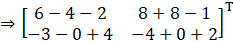
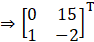
So,

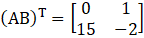
Exercise 5.5 Page No: 5.60

Solution:

Given

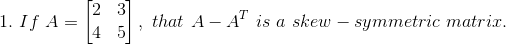
Consider,

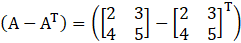
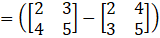
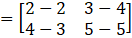
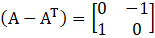
 … (i)

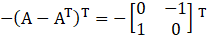
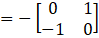
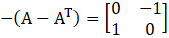
 … (ii)

From (i) and (ii) we can see that

A skew-symmetric matrix is a square matrix whose transpose equal to its negative, that is,

X = – X^T

So, A – A^T is a skew-symmetric.

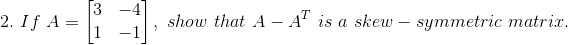
Solution:

Given

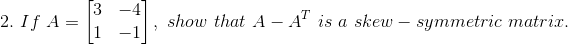
Consider,

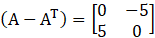
 … (i)

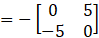
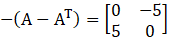
 … (ii)

From (i) and (ii) we can see that

A skew-symmetric matrix is a square matrix whose transpose equals its negative, that is,

X = – X^T

So, A – A^T is a skew-symmetric matrix.

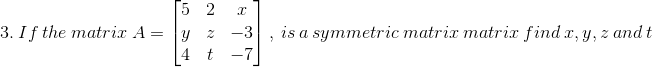
Solution:

Given,

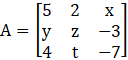
 is a symmetric matrix.

We know that A = [a_ij]_{m × n} is a symmetric matrix if a_ij = a_ji

So,

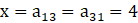
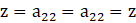
Hence, x = 4, y = 2, t = -3 and z can have any value.

4. Let. Find matrices X and Y such that X + Y = A, where X is a symmetric and y is a skew-symmetric matrix.

Solution:

Given,

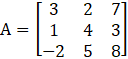
 Then

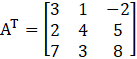
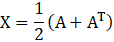
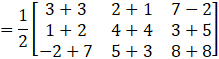
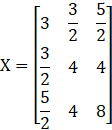
Now,

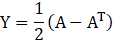
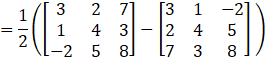
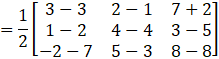
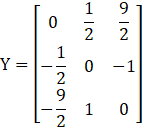
Now,

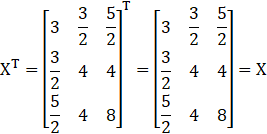
X is a symmetric matrix.

Now,

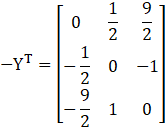
-Y ^T = Y

Y is a skew symmetric matrix.

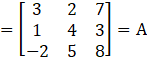
Hence, X + Y = A

RD Sharma Solutions for Class 12 Maths Chapter 5: Download PDF

RD Sharma Solutions for Class 12 Maths Chapter 5–Algebra of Matrices

Download PDF: RD Sharma Solutions for Class 12 Maths Chapter 5–Algebra of Matrices PDF

Chapterwise RD Sharma Solutions for Class 12 Maths :

• Chapter 1–Relation
• Chapter 2–Functions
• Chapter 3–Binary Operations
• Chapter 4–Inverse Trigonometric Functions
• Chapter 5–Algebra of Matrices
• Chapter 6–Determinants
• Chapter 7–Adjoint and Inverse of a Matrix
• Chapter 8–Solution of Simultaneous Linear Equations
• Chapter 9–Continuity
• Chapter 10–Differentiability
• Chapter 11–Differentiation
• Chapter 12–Higher Order Derivatives
• Chapter 13–Derivatives as a Rate Measurer
• Chapter 14–Differentials, Errors and Approximations
• Chapter 15–Mean Value Theorems
• Chapter 16–Tangents and Normals
• Chapter 17–Increasing and Decreasing Functions
• Chapter 18–Maxima and Minima
• Chapter 19–Indefinite Integrals

About RD Sharma

RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.

R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.