RD Sharma Solutions for Class 12 Maths Chapter 17–Increasing and Decreasing Functions

Class 12: Maths Chapter 17 solutions. Complete Class 12 Maths Chapter 17 Notes.

RD Sharma Solutions for Class 12 Maths Chapter 17–Increasing and Decreasing Functions

RD Sharma 12th Maths Chapter 17, Class 12 Maths Chapter 17 solutions

Exercise 17.1 Page No: 17.10

1. Prove that the function f(x) = log_e x is increasing on (0, ∞).

Solution:

Let x₁, x₂ ∈ (0, ∞)

We have, x₁ < x₂

⇒ log_e x₁ < log_e x₂

⇒ f (x₁) < f (x₂)

So, f(x) is increasing in (0, ∞)

2. Prove that the function f(x) = log_a x is increasing on (0, ∞) if a > 1 and decreasing on (0, ∞), if 0 < a < 1.

Solution:

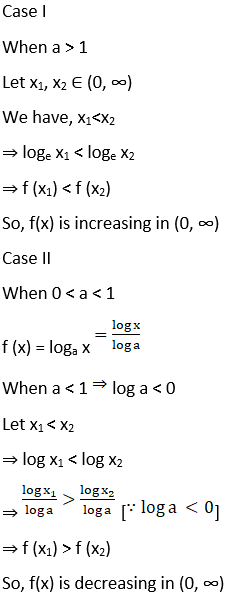
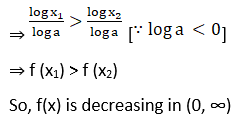
3. Prove that f(x) = ax + b, where a, b are constants and a > 0 is an increasing function on R.

Solution:

Given,

f (x) = ax + b, a > 0

Let x₁, x₂ ∈ R and x₁ > x₂

⇒ ax₁ > ax₂ for some a > 0

⇒ ax₁ + b> ax₂ + b for some b

⇒ f (x₁) > f(x₂)

Hence, x₁ > x₂ ⇒ f(x₁) > f(x₂)

So, f(x) is increasing function of R

4. Prove that f(x) = ax + b, where a, b are constants and a < 0 is a decreasing function on R.

Solution:

Given,

f (x) = ax + b, a < 0

Let x₁, x₂ ∈ R and x₁ > x₂

⇒ ax₁ < ax₂ for some a > 0

⇒ ax₁ + b < ax₂ + b for some b

⇒ f (x₁) < f(x₂)

Hence, x₁ > x₂⇒ f(x₁) < f(x₂)

So, f(x) is decreasing function of R

Exercise 17.2 Page No: 17.33

1. Find the intervals in which the following functions are increasing or decreasing.

(i) f (x) = 10 – 6x – 2x²

Solution:

(ii) f (x) = x² + 2x – 5

Solution:

(iii) f (x) = 6 – 9x – x²

Solution:

(iv) f(x) = 2x³ – 12x² + 18x + 15

Solution:

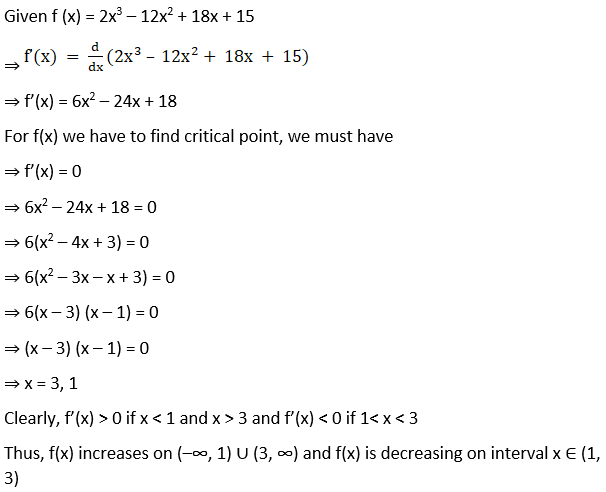
(v) f (x) = 5 + 36x + 3x² – 2x³

Solution:

Given f (x) = 5 + 36x + 3x² – 2x³

⇒

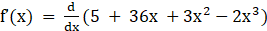
⇒ f’(x) = 36 + 6x – 6x²

For f(x) now we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 36 + 6x – 6x² = 0

⇒ 6(–x² + x + 6) = 0

⇒ 6(–x² + 3x – 2x + 6) = 0

⇒ –x² + 3x – 2x + 6 = 0

⇒ x² – 3x + 2x – 6 = 0

⇒ (x – 3) (x + 2) = 0

⇒ x = 3, – 2

Clearly, f’(x) > 0 if –2< x < 3 and f’(x) < 0 if x < –2 and x > 3

Thus, f(x) increases on x ∈ (–2, 3) and f(x) is decreasing on interval (–∞, –2) ∪ (3, ∞)

(vi) f (x) = 8 + 36x + 3x² – 2x³

Solution:

Given f (x) = 8 + 36x + 3x² – 2x³

Now differentiating with respect to x

⇒

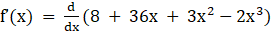
⇒ f’(x) = 36 + 6x – 6x²

For f(x) we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 36 + 6x – 6x² = 0

⇒ 6(–x² + x + 6) = 0

⇒ 6(–x² + 3x – 2x + 6) = 0

⇒ –x² + 3x – 2x + 6 = 0

⇒ x² – 3x + 2x – 6 = 0

⇒ (x – 3) (x + 2) = 0

⇒ x = 3, – 2

Clearly, f’(x) > 0 if –2 < x < 3 and f’(x) < 0 if x < –2 and x > 3

Thus, f(x) increases on x ∈ (–2, 3) and f(x) is decreasing on interval (–∞, 2) ∪ (3, ∞)

(vii) f(x) = 5x³ – 15x² – 120x + 3

Solution:

Given f(x) = 5x³ – 15x² – 120x + 3

Now by differentiating above equation with respect x, we get

⇒

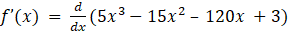
⇒ f’(x) = 15x² – 30x – 120

For f(x) we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 15x² – 30x – 120 = 0

⇒ 15(x² – 2x – 8) = 0

⇒ 15(x² – 4x + 2x – 8) = 0

⇒ x² – 4x + 2x – 8 = 0

⇒ (x – 4) (x + 2) = 0

⇒ x = 4, – 2

Clearly, f’(x) > 0 if x < –2 and x > 4 and f’(x) < 0 if –2 < x < 4

Thus, f(x) increases on (–∞,–2) ∪ (4, ∞) and f(x) is decreasing on interval x ∈ (–2, 4)

(viii) f(x) = x³ – 6x² – 36x + 2

Solution:

Given f (x) = x³ – 6x² – 36x + 2

⇒

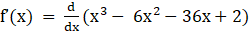
⇒ f’(x) = 3x² – 12x – 36

For f(x) we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 3x² – 12x – 36 = 0

⇒ 3(x² – 4x – 12) = 0

⇒ 3(x² – 6x + 2x – 12) = 0

⇒ x² – 6x + 2x – 12 = 0

⇒ (x – 6) (x + 2) = 0

⇒ x = 6, – 2

Clearly, f’(x) > 0 if x < –2 and x > 6 and f’(x) < 0 if –2< x < 6

Thus, f(x) increases on (–∞,–2) ∪ (6, ∞) and f(x) is decreasing on interval x ∈ (–2, 6)

(ix) f(x) = 2x³ – 15x² + 36x + 1

Solution:

Given f (x) = 2x³ – 15x² + 36x + 1

Now by differentiating above equation with respect x, we get

⇒

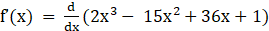
⇒ f’(x) = 6x² – 30x + 36

For f(x) we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 6x² – 30x + 36 = 0

⇒ 6 (x² – 5x + 6) = 0

⇒ 6(x² – 3x – 2x + 6) = 0

⇒ x² – 3x – 2x + 6 = 0

⇒ (x – 3) (x – 2) = 0

⇒ x = 3, 2

Clearly, f’(x) > 0 if x < 2 and x > 3 and f’(x) < 0 if 2 < x < 3

Thus, f(x) increases on (–∞, 2) ∪ (3, ∞) and f(x) is decreasing on interval x ∈ (2, 3)

(x) f (x) = 2x³ + 9x² + 12x + 20

Solution:

Given f (x) = 2x³ + 9x² + 12x + 20

Differentiating above equation we get

⇒

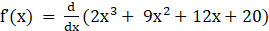
⇒ f’(x) = 6x² + 18x + 12

For f(x) we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 6x² + 18x + 12 = 0

⇒ 6(x² + 3x + 2) = 0

⇒ 6(x² + 2x + x + 2) = 0

⇒ x² + 2x + x + 2 = 0

⇒ (x + 2) (x + 1) = 0

⇒ x = –1, –2

Clearly, f’(x) > 0 if –2 < x < –1 and f’(x) < 0 if x < –1 and x > –2

Thus, f(x) increases on x ∈ (–2,–1) and f(x) is decreasing on interval (–∞, –2) ∪ (–2, ∞)

2. Determine the values of x for which the function f(x) = x² – 6x + 9 is increasing or decreasing. Also, find the coordinates of the point on the curve y = x² – 6x + 9 where the normal is parallel to the line y = x + 5.

Solution:

Given f(x) = x² – 6x + 9

⇒

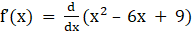
⇒ f’(x) = 2x – 6

⇒ f’(x) = 2(x – 3)

For f(x) let us find critical point, we must have

⇒ f’(x) = 0

⇒ 2(x – 3) = 0

⇒ (x – 3) = 0

⇒ x = 3

Clearly, f’(x) > 0 if x > 3 and f’(x) < 0 if x < 3

Thus, f(x) increases on (3, ∞) and f(x) is decreasing on interval x ∈ (–∞, 3)

Now, let us find coordinates of point

Equation of curve is f(x) = x² – 6x + 9

Slope of this curve is given by

3. Find the intervals in which f(x) = sin x – cos x, where 0 < x < 2π is increasing or decreasing.

Solution:

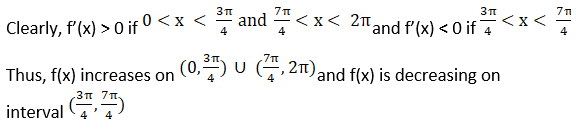
4. Show that f(x) = e^2x is increasing on R.

Solution:

Given f (x) = e^2x

⇒

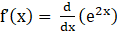
⇒ f’(x) = 2e^2x

For f(x) to be increasing, we must have

⇒ f’(x) > 0

⇒ 2e^2x > 0

⇒ e^2x > 0

Since, the value of e lies between 2 and 3

So, whatever be the power of e (that is x in domain R) will be greater than zero.

Thus f(x) is increasing on interval R

5. Show that f (x) = e^1/x, x ≠ 0 is a decreasing function for all x ≠ 0.

Solution:

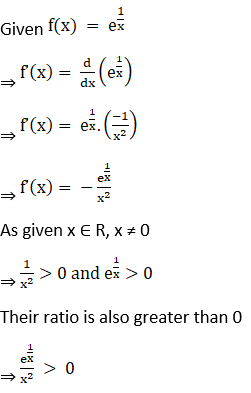
6. Show that f(x) = log_a x, 0 < a < 1 is a decreasing function for all x > 0.

Solution:

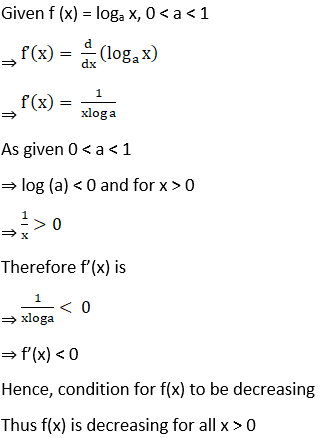
7. Show that f(x) = sin x is increasing on (0, π/2) and decreasing on (π/2, π) and neither increasing nor decreasing in (0, π).

Solution:

8. Show that f(x) = log sin x is increasing on (0, π/2) and decreasing on (π/2, π).

Solution:

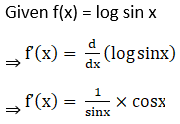
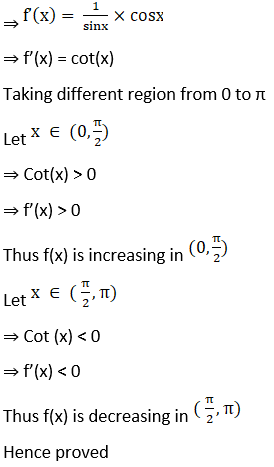
9. Show that f(x) = x – sin x is increasing for all x ϵ R.

Solution:

Given f (x) = x – sin x

⇒

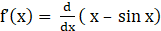
⇒ f’(x) = 1 – cos x

Now, as given x ϵ R

⇒ –1 < cos x < 1

⇒ –1 > cos x > 0

⇒ f’(x) > 0

Hence, condition for f(x) to be increasing

Thus f(x) is increasing on interval x ∈ R

10. Show that f(x) = x³ – 15x² + 75x – 50 is an increasing function for all x ϵ R.

Solution:

Given f(x) = x³ – 15x² + 75x – 50

⇒

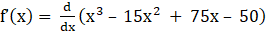
⇒ f’(x) = 3x² – 30x + 75

⇒ f’(x) = 3(x² – 10x + 25)

⇒ f’(x) = 3(x – 5)²

Now, as given x ϵ R

⇒ (x – 5)² > 0

⇒ 3(x – 5)² > 0

⇒ f’(x) > 0

Hence, condition for f(x) to be increasing

Thus f(x) is increasing on interval x ∈ R

11. Show that f(x) = cos² x is a decreasing function on (0, π/2).

Solution:

Given f (x) = cos² x

⇒

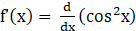
⇒ f’(x) = 2 cos x (–sin x)

⇒ f’(x) = –2 sin (x) cos (x)

⇒ f’(x) = –sin2x

Now, as given x belongs to (0, π/2).

⇒ 2x ∈ (0,
π)

⇒ Sin (2x)> 0

⇒ –Sin (2x) < 0

⇒ f’(x) < 0

Hence, condition for f(x) to be decreasing

Thus f(x) is decreasing on interval (0, π/2).

Hence proved

12. Show that f(x) = sin x is an increasing function on (–π/2, π/2).

Solution:

Given f (x) = sin x

⇒

⇒ f’(x) = cos x

Now, as given x ∈ (–π/2, π/2).

That is 4^th quadrant, where

⇒ Cos x> 0

⇒ f’(x) > 0

Hence, condition for f(x) to be increasing

Thus f(x) is increasing on interval (–π/2, π/2).

13. Show that f(x) = cos x is a decreasing function on (0, π), increasing in (–π, 0) and neither increasing nor decreasing in (–π, π).

Solution:

Given f(x) = cos x

⇒

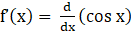
⇒ f’(x) = –sin x

Taking different region from 0 to 2π

Let x ∈ (0, π).

⇒ Sin(x) > 0

⇒ –sin x < 0

⇒ f’(x) < 0

Thus f(x) is decreasing in (0, π)

Let x ∈ (–π, o).

⇒ Sin (x) < 0

⇒ –sin x > 0

⇒ f’(x) > 0

Thus f(x) is increasing in (–π, 0).

Therefore, from above condition we find that

⇒ f (x) is decreasing in (0, π) and increasing in (–π, 0).

Hence, condition for f(x) neither increasing nor decreasing in (–π, π)

14. Show that f(x) = tan x is an increasing function on (–π/2, π/2).

Solution:

Given f (x) = tan x

⇒

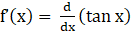
⇒ f’(x) = sec²x

Now, as given

x ∈ (–π/2, π/2).

That is 4^th quadrant, where

⇒ sec²x > 0

⇒ f’(x) > 0

Hence, Condition for f(x) to be increasing

Thus f(x) is increasing on interval (–π/2, π/2).

15. Show that f(x) = tan^–1 (sin x + cos x) is a decreasing function on the interval (π/4, π /2).

Solution:

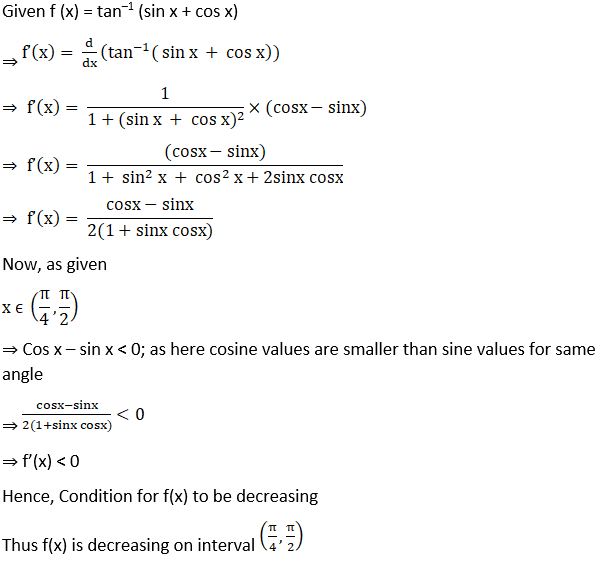
16. Show that the function f (x) = sin (2x + π/4) is decreasing on (3π/8, 5π/8).

Solution:

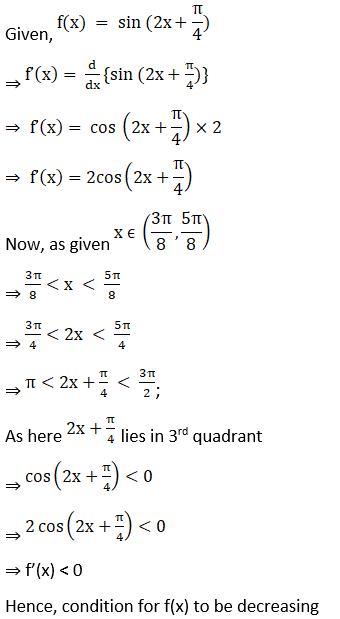
Thus f (x) is decreasing on the interval (3π/8, 5π/8).

17. Show that the function f(x) = cot^–1 (sin x + cos x) is decreasing on (0, π/4) and increasing on (π/4, π/2).

Solution:

Given f(x) = cot^–1 (sin x + cos x)

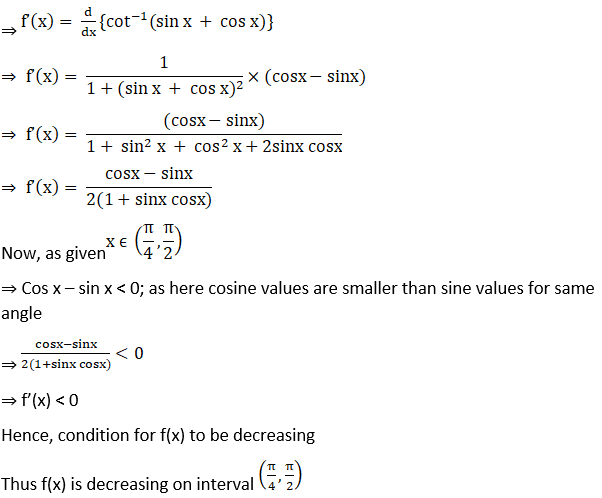
18. Show that f(x) = (x – 1) e^x + 1 is an increasing function for all x > 0.

Solution:

Given f (x) = (x – 1) e^x + 1

Now differentiating the given equation with respect to x, we get

⇒

⇒ f’(x) = e^x + (x – 1) e^x

⇒ f’(x) = e^x(1+ x – 1)

⇒ f’(x) = x e^x

As given x > 0

⇒ e^x > 0

⇒ x e^x > 0

⇒ f’(x) > 0

Hence, condition for f(x) to be increasing

Thus f(x) is increasing on interval x > 0

19. Show that the function x² – x + 1 is neither increasing nor decreasing on (0, 1).

Solution:

Given f(x) = x² – x + 1

Now by differentiating the given equation with respect to x, we get

⇒

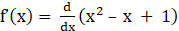
⇒ f’(x) = 2x – 1

Taking different region from (0, 1)

Let x ∈ (0, ½)

⇒ 2x – 1 < 0

⇒ f’(x) < 0

Thus f(x) is decreasing in (0, ½)

Let x ∈ (½, 1)

⇒ 2x – 1 > 0

⇒ f’(x) > 0

Thus f(x) is increasing in (½, 1)

Therefore, from above condition we find that

⇒ f (x) is decreasing in (0, ½)  and increasing in (½, 1)

Hence, condition for f(x) neither increasing nor decreasing in (0, 1)

20. Show that f(x) = x⁹ + 4x⁷ + 11 is an increasing function for all x ϵ R.

Solution:

Given f (x) = x⁹ + 4x⁷ + 11

Now by differentiating above equation with respect to x, we get

⇒

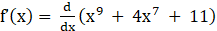
⇒ f’(x) = 9x⁸ + 28x⁶

⇒ f’(x) = x⁶(9x² + 28)

As given x ϵ R

⇒ x⁶ > 0 and 9x² + 28 > 0

⇒ x⁶ (9x² + 28) > 0

⇒ f’(x) > 0

Hence, condition for f(x) to be increasing

Thus f(x) is increasing on interval x ∈ R

RD Sharma Solutions for Class 12 Maths Chapter 17: Download PDF

RD Sharma Solutions for Class 12 Maths Chapter 17–Increasing and Decreasing Functions

Download PDF: RD Sharma Solutions for Class 12 Maths Chapter 17–Increasing and Decreasing Functions PDF

Chapterwise RD Sharma Solutions for Class 12 Maths :

• Chapter 1–Relation
• Chapter 2–Functions
• Chapter 3–Binary Operations
• Chapter 4–Inverse Trigonometric Functions
• Chapter 5–Algebra of Matrices
• Chapter 6–Determinants
• Chapter 7–Adjoint and Inverse of a Matrix
• Chapter 8–Solution of Simultaneous Linear Equations
• Chapter 9–Continuity
• Chapter 10–Differentiability
• Chapter 11–Differentiation
• Chapter 12–Higher Order Derivatives
• Chapter 13–Derivatives as a Rate Measurer
• Chapter 14–Differentials, Errors and Approximations
• Chapter 15–Mean Value Theorems
• Chapter 16–Tangents and Normals
• Chapter 17–Increasing and Decreasing Functions
• Chapter 18–Maxima and Minima
• Chapter 19–Indefinite Integrals

About RD Sharma

RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.

R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.