RD Sharma Solutions for Class 9 Maths Chapter 15–Area of Parallelograms and Triangles
RD Sharma Solutions for Class 9 Maths Chapter 15–Area of Parallelograms and Triangles

Class 9: Maths Chapter 15 solutions. Complete Class 9 Maths Chapter 15 Notes.

RD Sharma Solutions for Class 9 Maths Chapter 15–Area of Parallelograms and Triangles

RD Sharma 9th Maths Chapter 15, Class 9 Maths Chapter 15 solutions

Exercise 15.1 Page No: 15.3

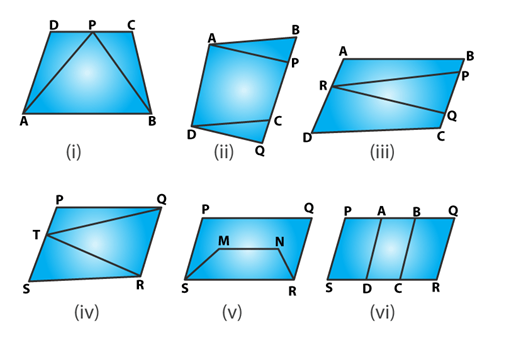
Question 1: Which of the following figures lie on the same base and between the same parallel. In such a case, write the common base and two parallels:

Solution:

(i) Triangle APB and trapezium ABCD are on the common base AB and between the same parallels AB and DC.

So,

Common base = AB

Parallel lines: AB and DC

(ii) Parallelograms ABCD and APQD are on the same base AD and between the same parallels AD and BQ.

Common base = AD

Parallel lines: AD and BQ

(iii) Consider, parallelogram ABCD and ΔPQR, lies between the same parallels AD and BC. But not sharing common base.

(iv) ΔQRT and parallelogram PQRS are on the same base QR and lies between same parallels QR and PS.

Common base = QR

Parallel lines: QR and PS

(v) Parallelograms PQRS and trapezium SMNR share common base SR, but not between the same parallels.

(vi) Parallelograms: PQRS, AQRD, BCQR are between the same parallels. Also,

Parallelograms: PQRS, BPSC, APSD are between the same parallels.

Exercise 15.2 Page No: 15.14

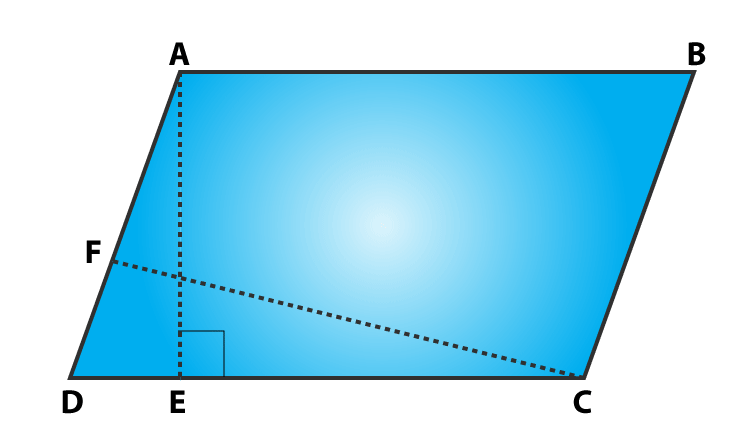
Question 1: If figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

Solution:

In parallelogram ABCD, AB = 16 cm, AE = 8 cm and CF = 10 cm

Since, opposite sides of a parallelogram are equal, then

AB = CD = 16 cm

We know, Area of parallelogram = Base x Corresponding height

Area of parallelogram ABCD:

CD x AE = AD x CF

16 x 18 = AD x 10

AD = 12.8

Measure of AD = 12.8 cm

Question 2: In Q.No. 1, if AD = 6 cm, CF = 10 cm and AE = 8 cm, find AB.

Solution: Area of a parallelogram ABCD:

From figure:

AD × CF = CD × AE

6 x 10 = CD x 8

CD = 7.5

Since, opposite sides of a parallelogram are equal.

=> AB = DC = 7.5 cm

Question 3: Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and CD respectively, then find the area of parallelogram AEFD.

Solution:

ABCD be a parallelogram.

Area of parallelogram = 124 cm2 (Given)

Consider a point P and join AP which is perpendicular to DC.

Now, Area of parallelogram EBCF = FC x AP and

Area of parallelogram AFED = DF x AP

Since F is the mid-point of DC, so DF = FC

From above results, we have

Area of parallelogram AEFD = Area of parallelogram EBCF = 1/2 (Area of parallelogram ABCD)

= 124/2

= 62

Area of parallelogram AEFD is 62 cm2.

Question 4: If ABCD is a parallelogram, then prove that

ar(Δ ABD) = ar(Δ BCD) = ar(Δ ABC)=ar(Δ ACD) = 1/2 ar(||gm ABCD)

Solution:

ABCD is a parallelogram.

When we join the diagonal of parallelogram, it divides it into two quadrilaterals.

Step 1: Let AC is the diagonal, then, Area (ΔABC) = Area (ΔACD) = 1/2(Area of llgm ABCD)

Step 2: Let BD be another diagonal

Area (ΔABD) = Area (ΔBCD) = 1/2( Area of llgm ABCD)

Now,

From Step 1 and step 2, we have

Area (ΔABC) = Area (ΔACD) = Area (ΔABD) = Area (ΔBCD) = 1/2(Area of llgm ABCD)

Hence Proved.

Exercise 15.3 Page No: 15.40

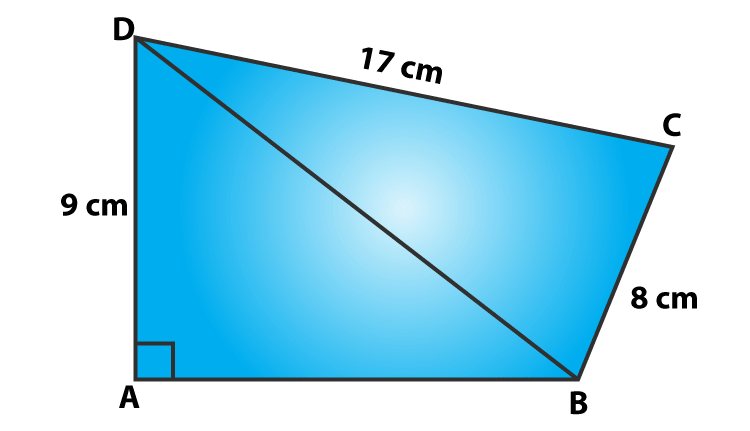
Question 1: In figure, compute the area of quadrilateral ABCD.

Solution:

A quadrilateral ABCD with DC = 17 cm, AD = 9 cm and BC = 8 cm (Given)

In right ΔABD,

Using Pythagorean Theorem,

AB2 + AD2 = BD2

152 = AB2 + 92

AB2 = 225−81=144

AB = 12

Area of ΔABD = 1/2(12×9) cm2 = 54 cm2

In right ΔBCD:

Using Pythagorean Theorem,

CD2 = BD2 + BC2

172 = BD2 + 82

BD2 = 289 – 64 = 225

or BD = 15

Area of ΔBCD = 1/2(8×17) cm2 = 68 cm2

Now, area of quadrilateral ABCD = Area of ΔABD + Area of ΔBCD

= 54 cm2 + 68 cm2

= 112 cm2

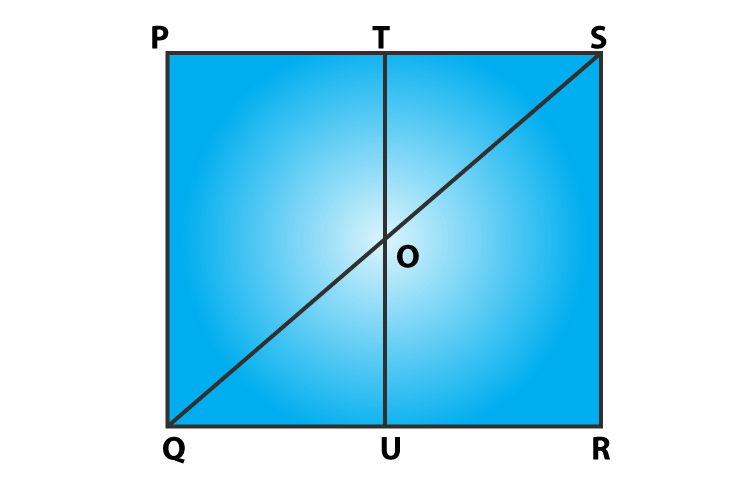
Question 2: In figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of ΔOTS if PQ = 8 cm.

Solution:

T and U are mid points of PS and QR respectively (Given)

Therefore, TU||PQ => TO||PQ

In ΔPQS ,

T is the mid-point of PS and TO||PQ

So, TO = 1/2 PQ = 4 cm

(PQ = 8 cm given)

Also, TS = 1/2 PS = 4 cm[PQ = PS, As PQRS is a square)

Now,

Area of ΔOTS = 1/2(TO×TS)

= 1/2(4×4) cm2

= 8cm2

Area of ΔOTS is 8 cm2.

Question 3: Compute the area of trapezium PQRS in figure.

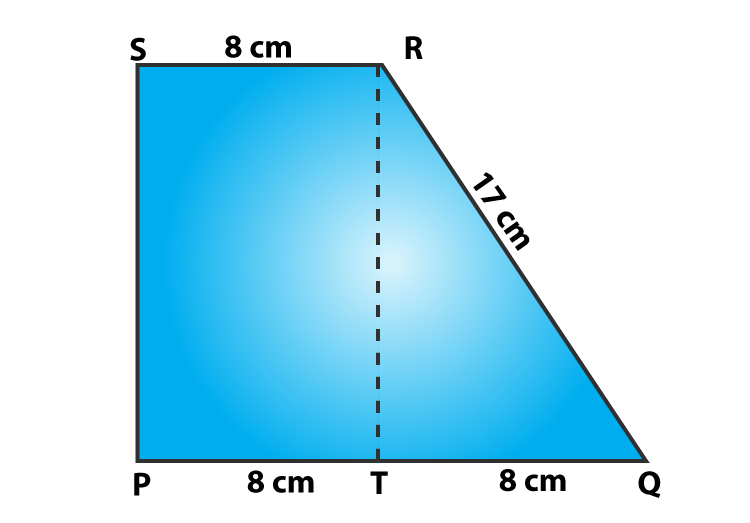
Solution:

From figure,

Area of trapezium PQRS = Area of rectangle PSRT + Area of ΔQRT

= PT × RT + 1/2 (QT×RT)

= 8 × RT + 1/2(8×RT)

= 12 RT

In right ΔQRT,

Using Pythagorean Theorem,

QR2 = QT2 + RT2

RT2 = QR2 − QT2

RT2 = 172−82 = 225

or RT = 15

Therefore, Area of trapezium = 12×15 cm2 = 180 cm2

Question 4: In figure, ∠AOB = 90o, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of ΔAOB.

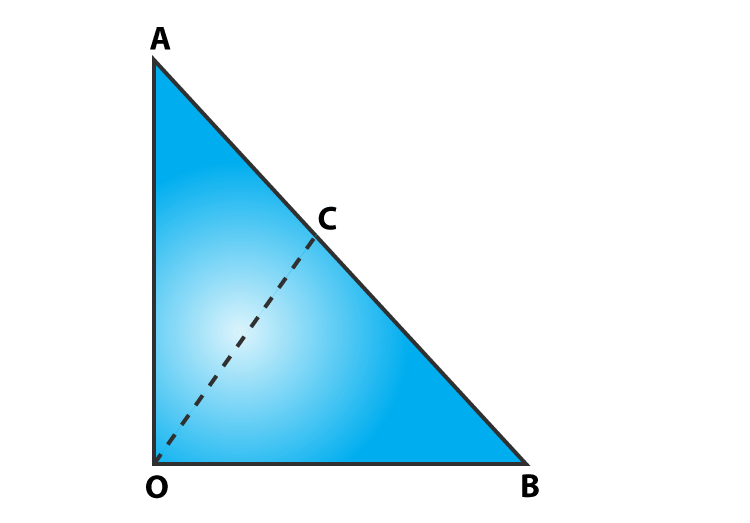
Solution:

Given: A triangle AOB, with ∠AOB = 90o, AC = BC, OA = 12 cm and OC = 6.5 cm

As we know, the midpoint of the hypotenuse of a right triangle is equidistant from the vertices.

So, CB = CA = OC = 6.5 cm

AB = 2 CB = 2 x 6.5 cm = 13 cm

In right ΔOAB:

Using Pythagorean Theorem, we get

AB2 = OB2 + OA2

132 = OB2 + 122

OB2 = 169 – 144 = 25

or OB = 5 cm

Now, Area of ΔAOB = ½(Base x height) cm2 = 1/2(12 x 5) cm2 = 30cm2

Question 5: In figure, ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm, and distance between AB and DC is 4 cm. Find the value of x and area of trapezium ABCD.

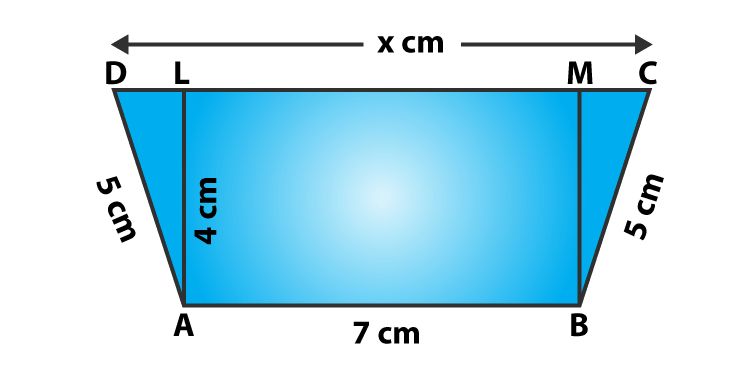
Solution:

Given: ABCD is a trapezium, where AB = 7 cm, AD = BC = 5 cm, DC = x cm, and

Distance between AB and DC = 4 cm

Consider AL and BM are perpendiculars on DC, then

AL = BM = 4 cm and LM = 7 cm.

In right ΔBMC :

Using Pythagorean Theorem, we get

BC2 = BM2 + MC2

25 = 16 + MC2

MC2 = 25 – 16 = 9

or MC = 3

Again,

In right Δ ADL :

Using Pythagorean Theorem, we get

AD2 = AL2 + DL2

25 = 16 + DL2

DL2 = 25 – 16 = 9

or DL = 3

Therefore, x = DC = DL + LM + MC = 3 + 7 + 3 = 13

=> x = 13 cm

Now,

Area of trapezium ABCD = 1/2(AB + CD) AL

= 1/2(7+13)4

= 40

Area of trapezium ABCD is 40 cm2.

Question 6: In figure, OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If OE = 2√5 cm, find the area of the rectangle.

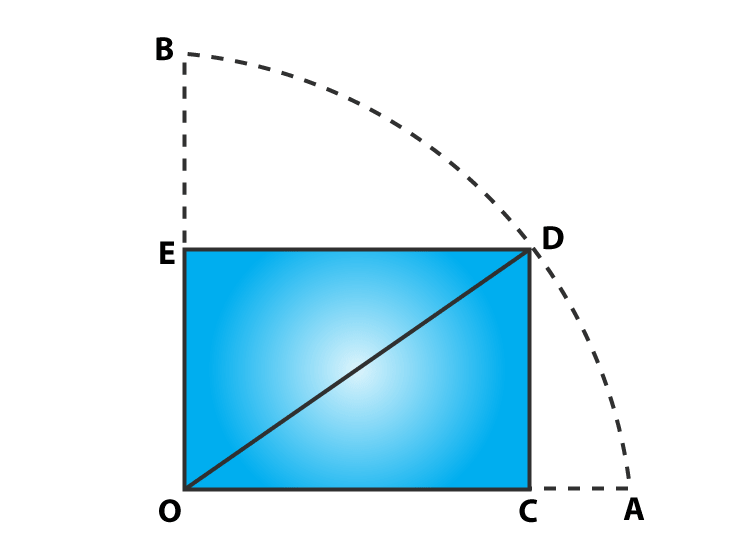
Solution:

From given:

Radius = OD = 10 cm and OE = 2√5 cm

In right ΔDEO,

By Pythagoras theorem

OD2 = OE2 + DE2

(10)2 = (2√5 )2 + DE2

100 – 20 = DE2

DE = 4√5

Now,

Area of rectangle OCDE = Length x Breadth = OE x DE = 2√5 x 4√5 = 40

Area of rectangle is 40 cm2.

Question 7: In figure, ABCD is a trapezium in which AB || DC. Prove that ar(ΔAOD) = ar(ΔBOC)

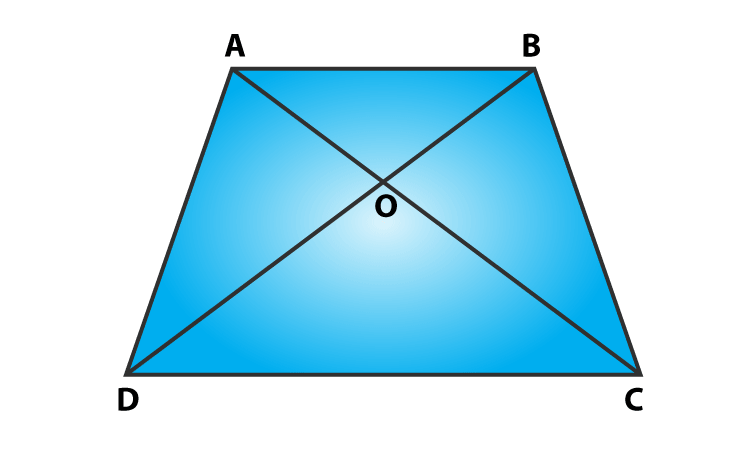
Solution:

ABCD is a trapezium in which AB || DC (Given)

To Prove: ar(ΔAOD) = ar(ΔBOC)

Proof:

From figure, we can observe that ΔADC and ΔBDC are sharing common base i.e. DC and between same parallels AB and DC.

Then, ar(ΔADC) = ar(ΔBDC) ……(1)

ΔADC is the combination of triangles, ΔAOD and ΔDOC. Similarly, ΔBDC is the combination of ΔBOC and ΔDOC triangles.

Equation (1) => ar(ΔAOD) + ar(ΔDOC) = ar(ΔBOC) + ar(ΔDOC)

or ar(ΔAOD) = ar(ΔBOC)

Hence Proved.

Question 8: In figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ΔADE) = ar(ΔBCF).

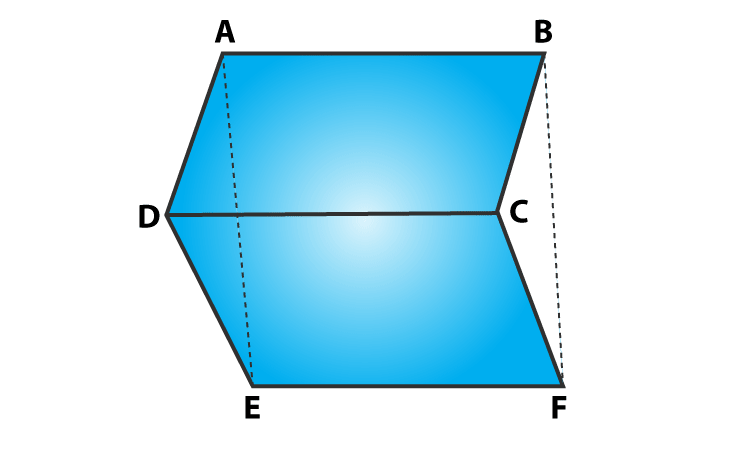
Solution:

Here, ABCD, CDEF and ABFE are parallelograms:

Which implies:

AD = BC

DE = CF and

AE = BF

Again, from triangles ADE and BCF:

AD = BC, DE = CF and AE = BF

By SSS criterion of congruence, we have

ΔADE ≅ ΔBCF

Since both the triangles are congruent, then ar(ΔADE) = ar(ΔBCF).

Hence Proved,

Question 9: Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that: ar(ΔAPB) x ar(ΔCPD) = ar(ΔAPD) x ar(ΔBPC).

Solution:

Consider: BQ and DR are two perpendiculars on AC.

To prove: ar(ΔAPB) x ar(ΔCPD) = ar(ΔAPD) x ar(ΔBPC).

Now,

L.H.S. = ar(ΔAPB) x ar(ΔCDP)

= (1/2 x AP × BQ) × (1/2 × PC × DR)

= (1/2 x PC × BQ) × (1/2 × AP × DR)

= ar(ΔAPD) x ar(ΔBPC)

= R.H.S.

Hence proved.

Question 10: In figure, ABC and ABD are two triangles on the base AB. If line segment CD is bisected by AB at O, show that ar(ΔABC) = ar(ΔABD).

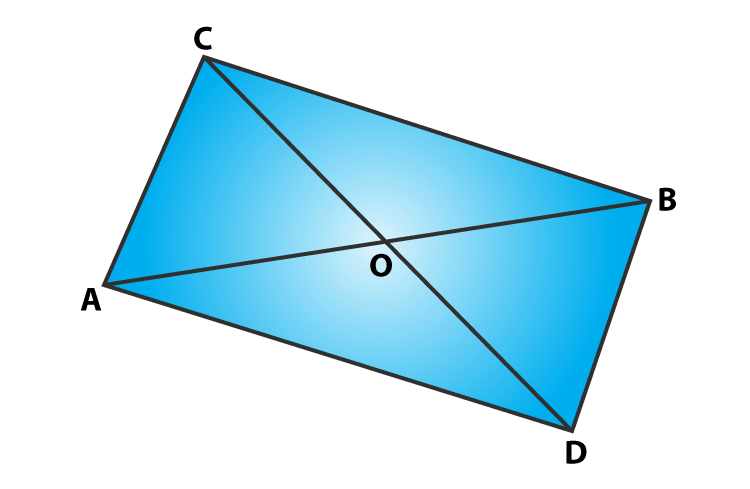
Solution:

Draw two perpendiculars CP and DQ on AB.

Now,

ar(ΔABC) = 1/2×AB×CP ⋅⋅⋅⋅⋅⋅⋅(1)

ar(ΔABD) = 1/2×AB×DQ ⋅⋅⋅⋅⋅⋅⋅(2)

To prove the result, ar(ΔABC) = ar(ΔABD), we have to show that CP = DQ.

In right angled triangles, ΔCPO and ΔDQO

∠CPO = ∠DQO = 90o

CO = OD (Given)

∠COP = ∠DOQ (Vertically opposite angles)

By AAS condition: ΔCP0 ≅ ΔDQO

So, CP = DQ …………..(3)

(By CPCT)

From equations (1), (2) and (3), we have

ar(ΔABC) = ar(ΔABD)

Hence proved.

Exercise VSAQs Page No: 15.55

Question 1: If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar(△ABC) : ar(△BDE).

Solution:

Given: ABC and BDE are two equilateral triangles.

We know, area of an equilateral triangle = √3/4 (side)2

Let “a” be the side measure of given triangle.

Find ar(△ABC):

ar(△ABC) = √3/4 (a) 2

Find ar(△BDE):

ar(△BDE) = √3/4 (a/2) 2

(D is the mid-point of BC)

Now,

ar(△ABC) : ar(△BDE)

or √3/4 (a) 2 : √3/4 (a/2) 2

or 1 : 1/4

or 4:1

This implies, ar(△ABC) : ar(△BDE) = 4:1

Question 2: In figure, ABCD is a rectangle in which CD = 6 cm, AD = 8 cm. Find the area of parallelogram CDEF.

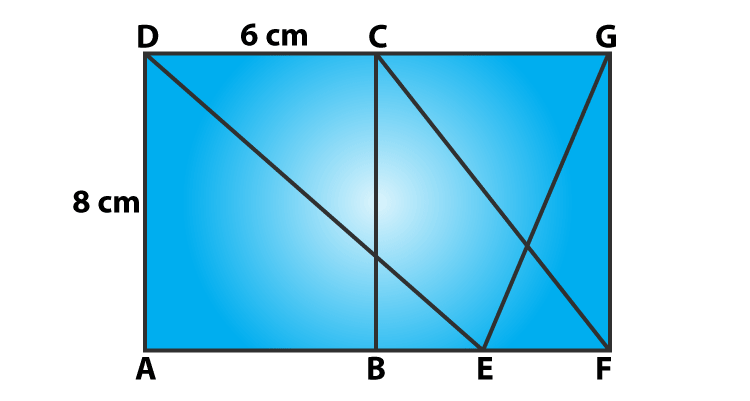
Solution:

ABCD is a rectangle, where CD = 6 cm and AD = 8 cm (Given)

From figure: Parallelogram CDEF and rectangle ABCD on the same base and between the same parallels, which means both have equal areas.

Area of parallelogram CDEF = Area of rectangle ABCD ….(1)

Area of rectangle ABCD = CD x AD = 6 x 8 cm2 = 48 cm2

Equation (1) => Area of parallelogram CDEF = 48 cm2.

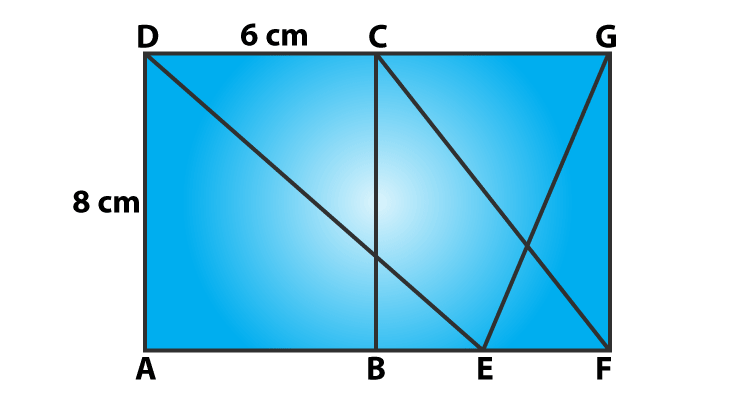
Question 3: In figure, find the area of ΔGEF.

Solution:

From figure:

Parallelogram CDEF and rectangle ABCD on the same base and between the same parallels, which means both have equal areas.

Area of CDEF = Area of ABCD = 8 x 6 cm2= 48 cm2

Again,

Parallelogram CDEF and triangle EFG are on the same base and between the same parallels, then

Area of a triangle = ½(Area of parallelogram)

In this case,

Area of a triangle EFG = ½(Area of parallelogram CDEF) = 1/2(48 cm2) = 24 cm2.

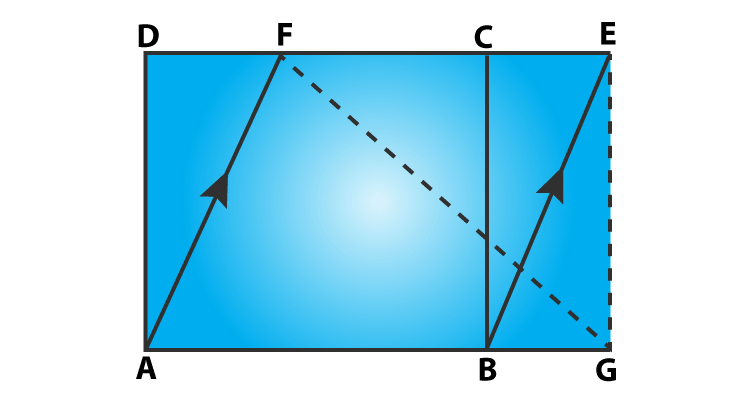
Question 4: In figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ΔEFG.

Solution:

From figure:

Parallelogram ABEF and rectangle ABCD on the same base and between the same parallels, which means both have equal areas.

Area of ABEF = Area of ABCD = 10 x 5 cm2= 50 cm2

Again,

Parallelogram ABEF and triangle EFG are on the same base and between the same parallels, then

Area of a triangle = ½(Area of parallelogram)

In this case,

Area of a triangle EFG = ½(Area of parallelogram ABEF) = 1/2(50 cm2) = 25 cm2.

Question 5: PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then find ar(△RAS).

Solution:

PQRS is a rectangle with PS = 5 cm and PR = 13 cm (Given)

In △PSR:

Using Pythagoras theorem,

SR2 = PR2 – PS2 = (13) 2 – (5) 2 = 169 – 25 = 114

or SR = 12

Now,

Area of △RAS = 1/2 x SR x PS

= 1/2 x 12 x 5

= 30

Therefore, Area of △RAS is 30 cm2.

RD Sharma Solutions for Class 9 Maths Chapter 15: Download PDF

RD Sharma Solutions for Class 9 Maths Chapter 15–Area of Parallelograms and Triangles

Download PDF: RD Sharma Solutions for Class 9 Maths Chapter 15–Area of Parallelograms and Triangles PDF

Chapterwise RD Sharma Solutions for Class 9 Maths :

About RD Sharma

RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.

R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.

Read More