Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 6- Trigonometry

Class 10: Maths Chapter 6 solutions. Complete Class 10 Maths Chapter 6 Notes.

Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 6- Trigonometry

Maharashtra Board 10th Maths Chapter 6, Class 10 Maths Chapter 6 solutions

Practice Set 6.1

Question 1.
If sin θ = 725, find the values of cos θ and tan θ.
Solution:
sin θ = 725 … [Given]
We know that,
sin² θ + cos² θ = 1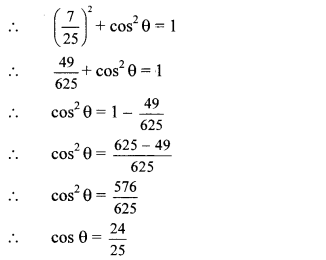

…[Taking square root of both sides] Now, tan θ = sinθcosθ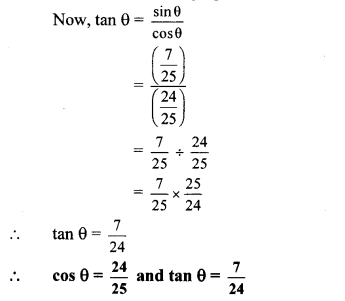

Alternate Method:
sin θ = 725 …(i) [Given]
Consider ∆ABC, where ∠ABC 90° and ∠ACB = θ.
sin θ = ABAC … (ii) [By definition]
∴ ABAC = 725 … [From (i) and (ii)]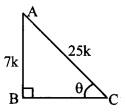

LetAB = 7k and AC = 25k
In ∆ABC, ∠B = 90°
∴ AB² + BC² = AC² … [Pythagoras theorem]
∴ (7k)² + BC² = (25k)²
∴ 49k² + BC² = 625k²
∴ BC² = 625k² – 49k²
∴ BC² = 576k²
∴ BC = 24k …[Taking square root of both sides]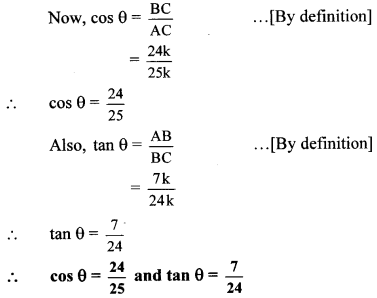

Question 2.
If tan θ = 34, find the values of sec θ and cos θ.
Solution: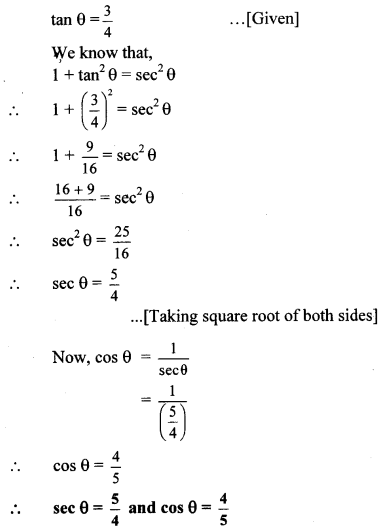

Alternate Method:
tan θ = 34 …(i)[Given]
Consider ∆ABC, where ∠ABC 90° and ∠ACB = θ.
tan θ = ABBC … (ii) [By definition]
∴ ABBC = 34 … [From (i) and (ii)]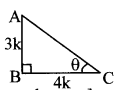

Let AB = 3k and BC 4k
In ∆ABC,∠B = 90°
∴ AB² + BC² = AC² …[Pythagoras theorem]
∴ (3k)² + (4k)² = AC²
∴ 9k² + 16k² = AC²
∴ AC² = 25k²
∴ AC = 5k …[Taking square root of both sides]

Question 3.
If cot θ = 409, find the values of cosec θ and sin θ
Solution:

..[Taking square root of both sides]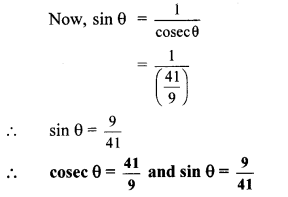

Alternate Method:
cot θ = 409 ….(i) [Given]
Consider ∆ABC, where ∠ABC = 90° and
∠ACB = θ
cot θ = BCAB …(ii) [By defnition]
∴ BCAB = 409 ….. [From (i) and (ii)]
Let BC = 40k and AB = 9k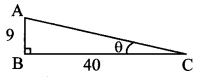

In ∆ABC, ∠B = 90°
∴ AB² + BC² = AC² … [Pythagoras theorem]
∴ (9k)² + (40k)² = AC²
∴ 81k² + 1600k² = AC²
∴ AC² = 1681k²
∴ AC = 41k … [Taking square root of both sides]

Question 4.
If 5 sec θ – 12 cosec θ = θ, find the values of sec θ, cos θ and sin θ.
Solution:
5 sec θ – 12 cosec θ = 0 …[Given]
∴ 5 sec θ = 12 cosec θ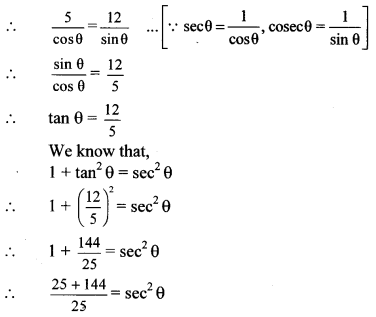

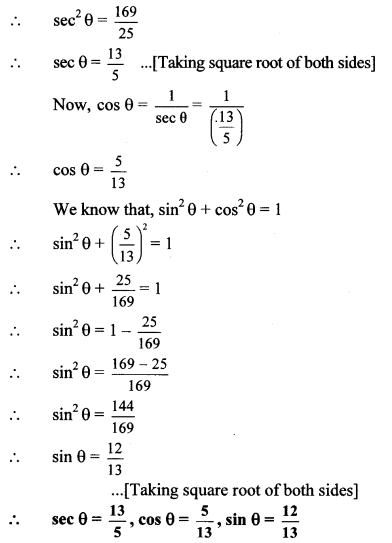
Question 5.
If tan θ = 1, then find the value of

Solution:
tan θ = 1 … [Given]
We know that, tan 45° = 1
∴ tan θ = tan 45°
∴ θ = 45°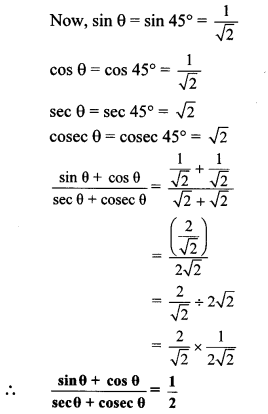

Question 6.
Prove that:
i. sin2θcosθ+cosθ=secθ
ii. cos² θ (1+ tan² θ) = 1
iii. 1−sinθ1+sinθ−−−−−√=secθ−tanθ
iv. (sec θ – cos θ) (cot θ + tan θ) tan θ. sec θ
v. cot θ + tan θ cosec θ. sec θ
vi. 1secθ−tanθ=secθ+tanθ
vii. sin⁴ θ – cos⁴ θ = 1 – 2 cos² θ
viii. secθ+tanθ=cosθ1−sinθ

Proof:
i. L.H.S. = sin2θcosθ+cosθ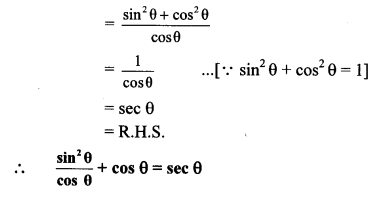

ii. L.H.S. = cos² θ(1 + tan² θ)
= cos² θ sec² θ …[∵ 1 + tan² θ = sec² θ]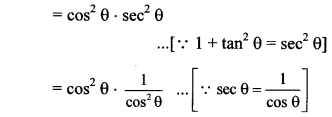

= 1
= R.H.S.
∴ cos² θ (1 + tan² θ) = 1

iv. L.H.S. = (sec θ – cos θ) (cot θ + tan θ)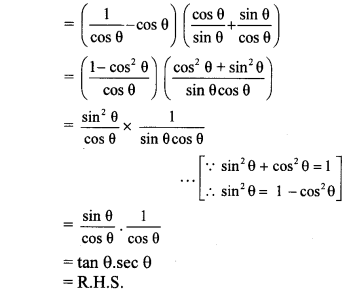

∴ (sec θ – cos θ) (cot θ + tan θ) = tan θ. sec θ

v. L.H.S. = cot θ + tan θ

∴ cot θ + tan θ = cosec θ.sec θ

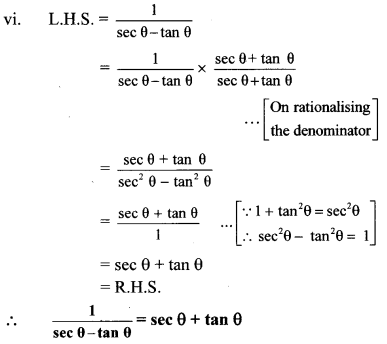
vii. L.H.S. = sin⁴ θ – cos⁴ θ
= (sin² θ)² – (cos² θ)²
= (sin² θ + cos² θ) (sin² θ – cos² θ)
= (1) (sin² θ – cos² θ) ….[∵ sin² θ + cos² θ = 1]
= sin² θ – cos² θ
= (1 – cos² θ) – cos² θ …[θ sin² θ = 1 – cos² θ]
= 1 – 2 cos² θ
= R.H.S.
∴ sin⁴ θ – cos⁴ θ = 1 – 2 cos² θ

viii. L.H.S. = sec θ + tan θ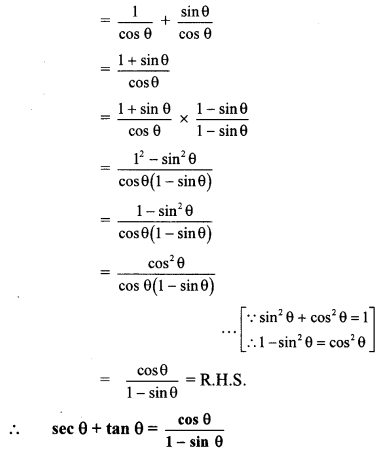

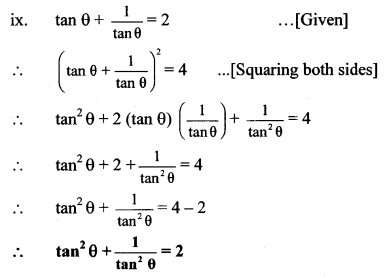
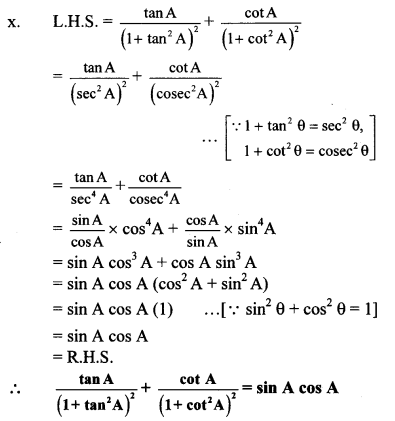
xi. L.H.S. = sec⁴ A (1 – sin⁴ A) – 2 tan² A
= sec⁴ A [1² – (sin² A)²] – 2 tan² A
= sec⁴ A (1 – sin²A) (1 + sin² A) – 2 tan² A
= sec⁴ A cos²A (1 + sin² A) – 2 tan²A
[ ∵ sin² θ + cos² θ = 1 ,∵ 1 – sin² θ = cos² θ]

Question 1.
Fill in the blanks with reference to the figure given below. (Textbook pg. no. 124)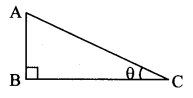

Solution:

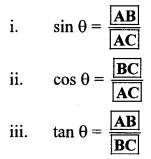
Question 2.
Complete the relations in ratios given below. (Textbook pg, no. 124)

Solution:
i. sinθcosθ = [tan θ]
ii. sin θ = cos (90 – θ)
iii. cos θ = (90 – θ)
iv. tan θ × tan (90 – θ) = 1

Question 3.
Complete the equation. (Textbook pg. no, 124)
sin² θ + cos² θ = [______]
Solution:
sin² θ + cos² θ = [1]

Question 4.
Write the values of the following trigonometric ratios. (Textbook pg. no. 124)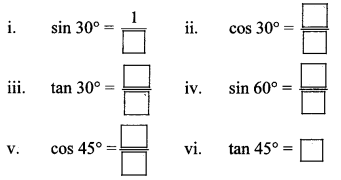

Solution: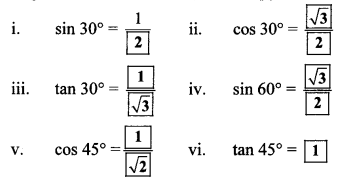

Practice Set 6.2

Question 1.
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
Solution:
Let AB represent the height of the church and point C represent the position of the person.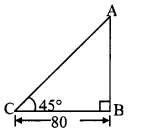

BC = 80 m
Angle of elevation = ∠ACB = 45°
In right angled ∆ABC,
tan 45° = ABBC … [By definition]
∴ 1 = AB80
∴ AB = 80m
∴ The height of the church is 80 m.

Question 2.
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse. ( 3–√ = 1.73)
Solution:
Let AB represent the height of lighthouse and point C represent the position of the ship.
AB = 90 m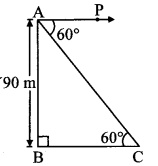

Angle of depression = ∠PAC = 60°
Now, ray AP || seg BC
∴ ∠ACB = ∠PAC … [Alternate angles]
∴ ∠ACB = 60°
In right angled ∆ABC,
tan 60° = ABBC … [By definition]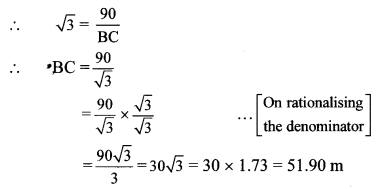

∴ The ship is 51.90 m away from the lighthouse.

Question 3.
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building?
Solution:
Let AB and CD represent the heights of the two buildings, and BD represent the width of the road.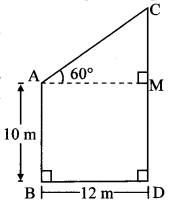

Draw seg AM ⊥ seg CD.
Angle of elevation = ∠CAM = 60°
AB = 10 m
BD= 12 m
In ꠸ABDM,
∠B = ∠D = 90°
∠M = 90° … [seg AM ⊥ seg CD]
∴ ∠A = 90° … [Remaining angle of ꠸ABDM]
∴ ꠸ABDM is a rectangle …. [Each angle is 90°]
∴ AM = BD = 12 m opposite sides
DM = AB = 10 m of a rectangle
In right angled ∆AMC,
tan 60° = CMAM …[By definition]
∴ 3–√ = CM12
∴ CM = 123–√ m
Now, CD = DM + CM … [C – M – D]
∴ CD = (10 + 123–√)m
= 10 + 12 × 1.73
= 10 + 20.76 = 30.76
∴ The height of the second building is 30.76 m.

Question 4.
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops is 22 metre. Find the angle made by the wire with the horizontal.
Solution:
Let AB and CD represent the heights of two poles, and AC represent the length of the wire.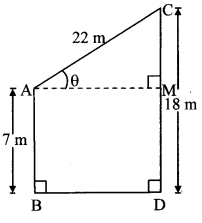

Draw seg AM ⊥ seg CD.
Angle of elevation = ∠CAM = θ
AB = 7 m
CD = 18 m
AC = 22 m
In ꠸ABDM,
∠B = ∠D = 90°
∠M = 90° …[seg AM ⊥ seg CD]
∴ ∠A = 90° … [Remaining angle of ꠸ABDM]
∴ □ABDM is a rectangle. … [Each angle is 90°]
∴ DM = AB = 7 m … [Opposite sides of a rectangle]
Now, CD = CM + DM … [C – M – D]
∴ 18 = CM + 7
∴ CM = 18 – 7 = 11 m
In right angled ∆AMC,
sin θ = CMAC …..[By definition]
∴ sin θ = 1122 = 12
But, sin 30° = 12
∴ θ = 30°
∴ The angle made by the wire with the horizontal is 30°.

Question 5.
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
Solution:
Let AB represent the height of the tree.
Suppose the tree broke at point C and its top touches the ground at D.
AC is the broken part of the tree which takes position CD such that ∠CDB = 60°
∴ AC = CD …(i)
BD = 20 m
In right angled ∆CBD,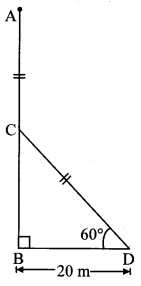

tan 60° = BCBD … [By definition]
∴ 3–√ = BC20
∴ BC = 203–√ m
Also, cos 60° = BCCD … [By definition]
∴ 12 = 20CD
∴ CD = 20 × 2 = 40 m
∴ AC = 40 m …[From(i)]
Now, AB = AC + BC ….[A – C – B]
= 40 + 203–√
= 40 + 20 × 1.73
= 40 + 34.6
= 74.6
∴ The height of the tree is 74.6 m.

Question 6.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string. (3–√ = 1.73)
Solution:
Let AB represent the height at which kite is flying and point C represent the point where the string is tied at the ground.
∠ACB is the angle made by the string with the ground.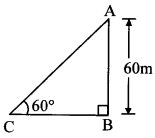

∠ACB = 60°
AB = 60 m
In right angled ∆ABC,
sin 60° = ABAC … [By definition]

∴ AC = 40 3–√ = 40 × 1.73 = 69.20 m
∴ The length of the string is 69.20 m.

Download PDF

Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 6- Trigonometry

Download PDF: Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 6- Trigonometry PDF

Chapterwise Maharashtra Board Solutions Class 10 Maths (Part 2) :

• Chapter 1- Similarity
• Chapter 2- Pythagoras Theorem
• Chapter 3- Circle
• Chapter 4- Geometric Constructions
• Chapter 5- Co-ordinate Geometry
• Chapter 6- Trigonometry
• Chapter 7- Mensuration

FAQs

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC. 

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.

Read More

• NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry
• RD Sharma Solutions for Class 10 Maths Chapter 6–Trigonometric Identities
• RD Sharma Solutions for Class 11 Maths Chapter 5–Trigonometric Functions
• RD Sharma Solutions for Class 12 Maths Chapter 4–Inverse Trigonometric Functions
• RD Sharma Solutions for Class 10 Maths Chapter 5–Trigonometric Ratios

IndCareer Board Book Solutions App

IndCareer Board Book App provides complete study materials for students from classes 1 to 12 of Board. The App contains complete solutions of NCERT books, notes, and other important materials for students. Download the IndCareer Board Book Solutions now.