Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 1- Similarity

Class 10: Maths Chapter 1 solutions. Complete Class 10 Maths Chapter 1 Notes.

Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 1- Similarity

Maharashtra Board 10th Maths Chapter 1, Class 10 Maths Chapter 1 solutions

Question 1.
Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
Solution:
Let the base, height and area of the first triangle be b₁, h₁, and A₁ respectively.
Let the base, height and area of the second triangle be b₂, h₂ and A₂ respectively.

[Since Ratio of areas of two triangles is equal to the ratio of the product of their bases and corresponding heights]
∴ The ratio of areas of the triangles is 3:4.

Question 2.
In the adjoining figure, BC ± AB, AD _L AB, BC = 4, AD = 8, then find A(ΔABC)A(ΔADB)

Solution:
∆ABC and ∆ADB have same base AB.

[Since Triangles having equal base]

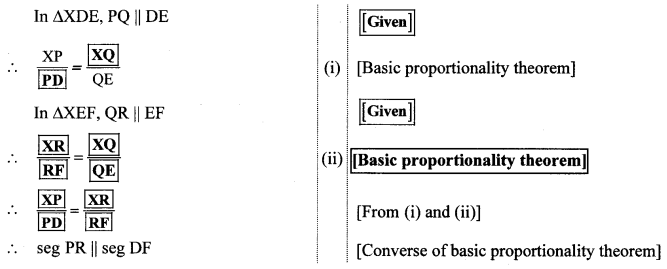
Question 3.
In the adjoining figure, seg PS ± seg RQ, seg QT ± seg PR. If RQ = 6, PS = 6 and PR = 12, then find QT.

Solution:
In ∆PQR, PR is the base and QT is the corresponding height.
Also, RQ is the base and PS is the corresponding height.
A(ΔPQR)A(ΔPQR)=PR×QTRQ×PS [Ratio of areas of two triangles is equal to the ratio of the product of their bases and corresponding heights]
∴ 11=PR×QTRQ×PS
∴ PR × QT = RQ × PS
∴ 12 × QT = 6 × 6
∴ QT = 3612
∴ QT = 3 units

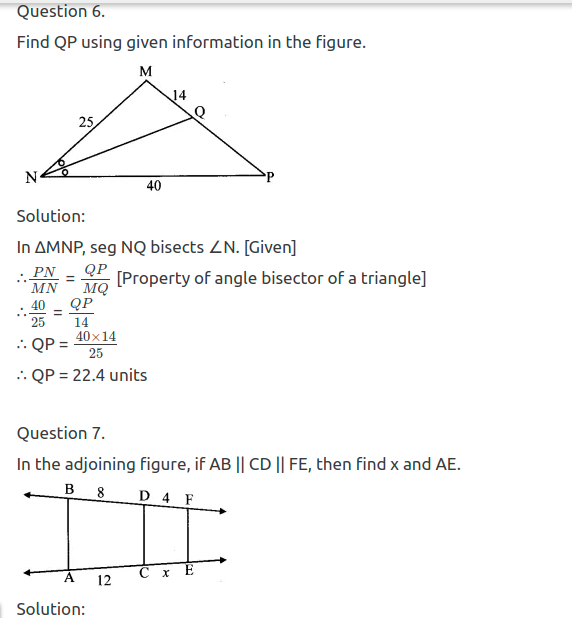
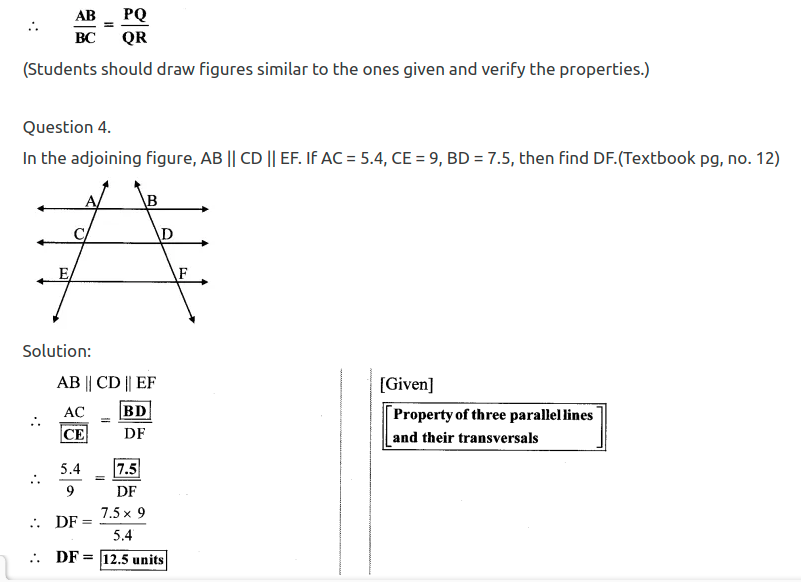
Question 4.
In the adjoining figure, AP ⊥ BC, AD || BC, then find A(∆ABC) : A(∆BCD).

Solution:
Draw DQ ⊥ BC, B-C-Q.

AD || BC [Given]
∴ AP = DQ   (i)  [Perpendicular distance between two parallel lines is the same]
∆ABC and ∆BCD have same base BC.

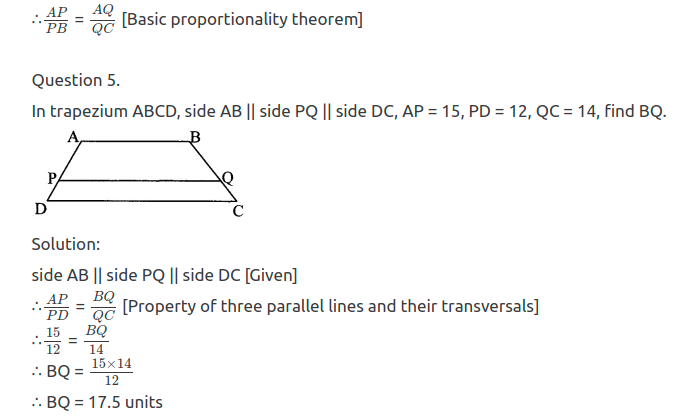
Question 5.
In the adjoining figure, PQ ⊥ BC, AD ⊥ BC, then find following ratios.

Solution:
i. ∆PQB and tPBC have same height PQ.

ii. ∆PBC and ∆ABC have same base BC.

iii. ∆ABC and ∆ADC have same height AD.

Question 1.
Find A(ΔABC)A(ΔAPQ)

Solution:
In ∆ABC, BC is the base and AR is the height.
In ∆APQ, PQ is the base and AR is the height.

Practice Set 1.2

Question 1.
Given below are some triangles and lengths of line segments. Identify in which figures, ray PM is the bisector of ∠QPR.

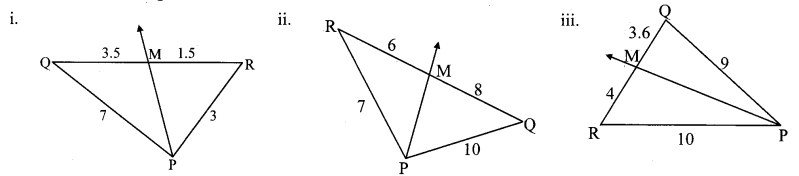
Solution:
In ∆ PQR,

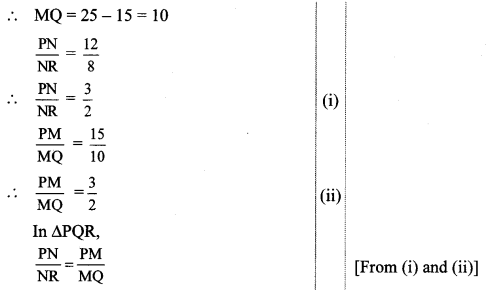
∴ line NM || side RQ [Converse of basic proportionality theorem]

Question 3.
In ∆MNP, NQ is a bisector of ∠N. If MN = 5, PN = 7, MQ = 2.5, then find QP.

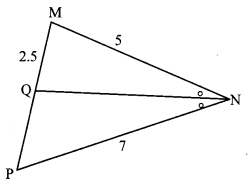
Solution:
In ∆MNP, NQ is the bisector of ∠N. [Given]

Question 4.
Measures of some angles in the figure are given. Prove that APPB = AQQC

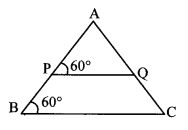
Solution:
Proof
∠APQ = ∠ABC = 60° [Given]
∴ ∠APQ ≅ ∠ABC
∴ side PQ || side BC (i) [Corresponding angles test]
In ∆ABC,
sidePQ || sideBC [From (i)]

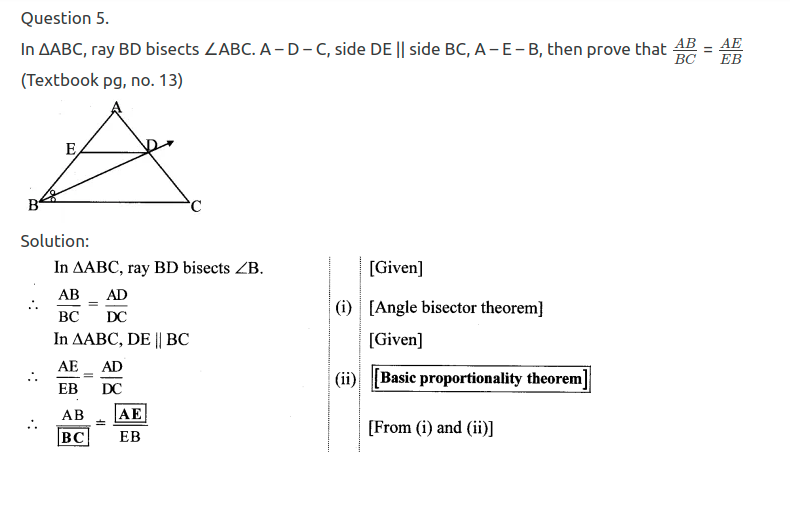
Question 11.
In ∆ABC, ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB = seg AC, then prove that ED || BC.

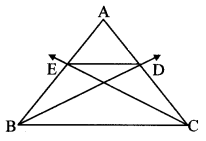
Solution:
In ∆ABC, ray BD bisects ∠ABC. [Given]

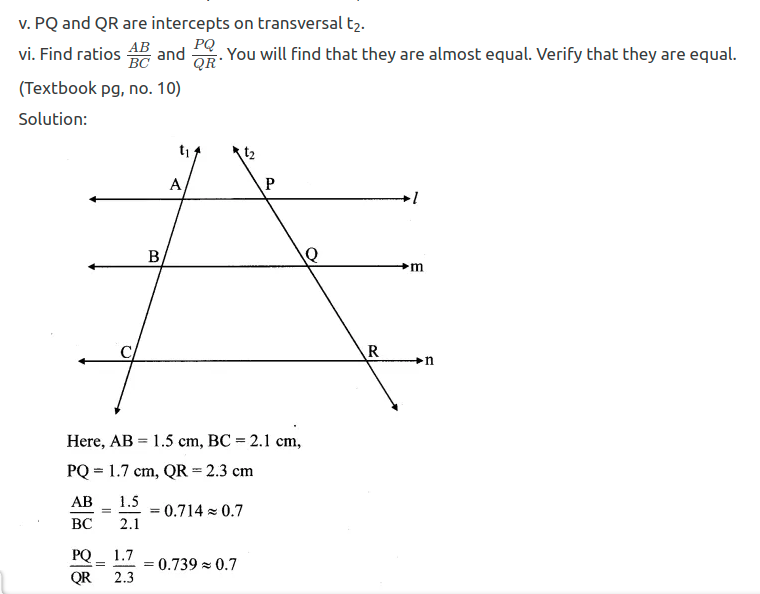
Note: Students should bisect the remaining angles and verify that the ratios are equal.

Question 2.
Write another proof of the above theorem (property of an angle bisector of a triangle). Use the following properties and write the proof.
i. The areas of two triangles of equal height are proportional to their bases.
ii. Every point on the bisector of an angle is equidistant from the sides of the angle. (Textbook pg. no. 9)

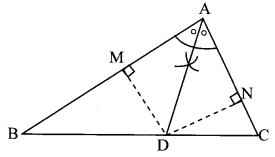
Given: In ∆CAB, ray AD bisects ∠A.

Practice Set 1.3

Question 1.
In the adjoining figure, ∠ABC = 75°, ∠EDC = 75°. State which two triangles are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.

Solution:
In ∆ABC and ∆EDC,
∠ABC ≅ ∠EDC [Each angle is of measure 75°]
∠ACB ≅ ∠ECD [Common angle]
∴ ∆ABC ~ ∆EDC [AA test of similarity]
One to one correspondence is
ABC ↔ EDC

Question 2.
Are the triangles in the adjoining figure similar? If yes, by which test?

Solution:
In ∆PQR and ∆LMN,

Question 3.
As shown in the adjoining figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m, then how long will be the shadow of the bigger pole at the same time?

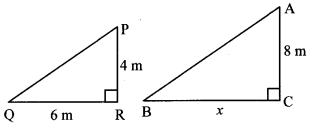
Solution:
Here, AC and PR represents the bigger and smaller poles, and BC and QR represents their shadows respectively.
Now, ∆ACB – ∆PRQ [ ∵ Vertical poles and their shadows form similar figures]

Question 4.
In ∆ABC, AP ⊥ BC, BQ ⊥ AC, B – P – C, A – Q – C, then prove that ∆CPA – ∆CQB. If AP = 7, BQ = 8, BC = 12, then find AC.

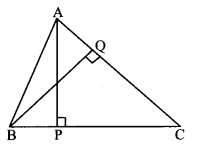
Solution:
In ∆CPA and ∆CQB,
∠CPA ≅ ∠CQB [Each angle is of measure 90°]
∠ACP ≅ ∠BCQ [Common angle]
∴ ∆CPA ~ ∆CQB [AA test of similarity]

Question 5.
Given: In trapezium PQRS, side PQ || side SR, AR = 5 AP, AS = 5 AQ, then prove that SR = 5 PQ.

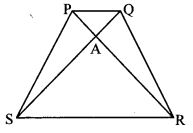
Solution:
side PQ || side SR [Given]
and seg SQ is their transversal.
∴ ∠QSR = ∠SQP [Altemate angles]
∴ ∠ASR = ∠AQP (i) [Q – A – S]
In ∆ASR and ∆AQP,
∠ASR = ∠AQP [From (i)]
∠SAR ≅ ∠QAP [Vertically opposite angles]
∆ASR ~ ∆AQP [AA test of similarity]
∴ ASAQ = SRPQ (ii) [Corresponding sides of similar triangles]
But, AS = 5 AQ [Given]
∴ ASAQ = 51 (iii)
∴ SRPQ = 51 [From (ii) and (iii)]
∴ SR = 5 PQ

Question 6.
Id trapezium ABCD (adjoining figure), side AB || side DC, diagonals AC and BD intersect in point O. If AB = 20, DC = 6, OB = 15, then find OD.

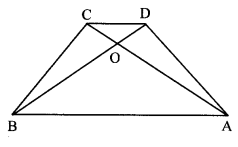
Solution:
side AB || side DC [Given]
and seg BD is their transversal.
∴ ∠DBA ≅ ∠BDC [Alternate angles]
∴ ∠OBA ≅ ∠ODC (i) [D – O – B]
In ∆OBA and ∆ODC
∠OBA ≅ ∠ODC [From (i)]
∠BOA ≅ ∠DOC [Vertically opposite angles]
∴ ∆OBA ~ ∆ODC [AA test of similarity]

Question 7.
꠸ ABCD is a parallelogram. Point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

Solution:
Proof:
꠸ ABCD is a parallelogram. [Given]
∴ side AB || side CD [Opposite sides of a parallelogram]
∴ side AT || side CD [A – B – T]
and seg DT is their transversal.
∴ ∠ATD ≅ ∠CDT [Alternate angles]
∴ ∠BTE ≅ ∠CDE (i) [A – B – T, T – E – D]
In ∆BTE and ∆CDE,
∠BTE ≅ ∠CDE [From (i)]
∠BET ≅ ∠CED [Vertically opposite angles]
∴ ∆BTE ~ ∆CDE. [AA test of similarity]
∴ TEDE = BECE [Corresponding sides of similar triangles]
∴ DE × BE = CE × TE

Question 8.
In the adjoining figure, seg AC and seg BD intersect each other in point P and APCP = BPDP Prove that, ∆ABP ~ ∆CDP

Solution:
Proof:
In ∆ABP and ∆CDP,
APCP = BPDP [Given]
∠APB ≅ ∠CPD [Vertically opposite angles]
∴ ∆ABP ~ ∆CDP [SAS test of similarity]

Question 9.
In the adjoining figure, in ∆ABC, point D is on side BC such that, ∠BAC = ∠ADC. Prove that, CA² = CB × CD,

Solution:
Proof:
In ∆BAC and ∆ADC,
∠BAC ≅ ∠ADC [Given]
∠BCA ≅ ∠ACD [Common angle]
∴ ∆BAC ~ ∆ADC [AA test of similarity]
∴ CACD = CBCA [Corresponding sides of similar triangles]
∴ CA × CA = CB × CD
∴ CA² = CB × CD

Question 1.
In the adjoining figure, BP ⊥ AC, CQ ⊥ AB, A – P – C, A – Q – B, then prove that ∆APB and ∆AQC are similar. (Textbook pg. no. 20)

Solution:

2. SAS test for similarity of triangles:
For a given correspondence, if two pairs of corresponding sides are in the same proportion and the angle between them is congruent, then the two triangles are similar.

In the given figure, if ABPQ = BCQR, and ∠B ≅∠Q, then ∆ABC ~ ∆PQR

3. SSS test for similarity of triangles:
For a given correspondence, if three sides of one triangle are in proportion with the corresponding three sides of the another triangle, then the two triangles are similar.

In the given figure, if ABPQ = BCQR = ACPR, then ∆ABC ~ ∆PQR

Properties of similar triangles:

1. Reflexivity: ∆ABC ~ ∆ABC
2. Symmetry : If ∆ABC ~ ∆DEF, then ∆DEF ~ ∆ABC.
3. Transitivity: If ∆ABC ~ ∆DEF and ∆DEF ~ ∆GHI, then ∆ABC ~ ∆GHI.

Practice Set 1.4

Question 1.
The ratio of corresponding sides of similar triangles is 3 : 5, then find the ratio of their areas.
Solution:
Let the corresponding sides of similar triangles be S₁ and S₂.
Let A₁ and A₂ be their corresponding areas.

∴ Ratio of areas of similar triangles = 9 : 25

Question 2.
If ∆ABC ~ ∆PQR and AB : PQ = 2:3, then fill in the blanks.
Solution:

Question 3.
If ∆ABC ~ ∆PQR, A(∆ABC) = 80, A(∆PQR) = 125, then fill in the blanks.
Solution:

Question 5.
Areas of two similar triangles are 225 sq. cm. and 81 sq. cm. If a side of the smaller triangle is 12 cm, then find corresponding side of the bigger triangle.
Solution:
Let the areas of two similar triangles be A₁ and A₂.
A₁ = 225 sq. cm. A₂ = 81 sq. cm.
Let the corresponding sides of triangles be S₁ and S₂ respectively.
S₁ = 12 cm

∴ The length of the corresponding side of the bigger triangle is 20 cm.

Question 6.
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC): A(∆DEF) = 1:2 and AB = 4, find DE.
Solution:
In ∆ABC and ∆DEF,

Question 7.
In the adjoining figure, seg PQ || seg DE, A(∆PQF) = 20 sq. units, PF = 2 DP, then find A (꠸ DPQE) by completing the following activity.
Solution:
A(∆PQF) = 20 sq.units, PF = 2 DP, [Given]
Let us assume DP = x.
∴ PF = 2x

Download PDF

Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 1- Similarity

Download PDF: Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 1- Similarity PDF

Chapterwise Maharashtra Board Solutions Class 10 Maths (Part 2) :

• Chapter 1- Similarity
• Chapter 2- Pythagoras Theorem
• Chapter 3- Circle
• Chapter 4- Geometric Constructions
• Chapter 5- Co-ordinate Geometry
• Chapter 6- Trigonometry
• Chapter 7- Mensuration

FAQs

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC. 

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.

Read More

• RS Aggarwal Solutions for Class 7 Maths Chapter 16–Congruence
• NCERT Solutions for 9th Class Maths : Chapter 7 Triangles
• RS Aggarwal Solutions for Class 7 Maths Chapter 17–Constructions
• RS Aggarwal Solutions for Class 7 Maths Chapter 15–Properties of Triangles
• RD Sharma Solutions for Class 7 Maths Chapter 16–Congruence

IndCareer Board Book Solutions App

IndCareer Board Book App provides complete study materials for students from classes 1 to 12 of Board. The App contains complete solutions of NCERT books, notes, and other important materials for students. Download the IndCareer Board Book Solutions now.