Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 4- Geometric Constructions

Class 10: Maths Chapter 4 solutions. Complete Class 10 Maths Chapter 4 Notes.

Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 4- Geometric Constructions

Maharashtra Board 10th Maths Chapter 4, Class 10 Maths Chapter 4 solutions

Practice Set 4.1

Question 1.
∆ABC ~ ∆LMN. In ∆ABC, AB = 5.5 cm, BC = 6 cm, CA = 4.5 cm. Construct ∆ABC and ∆LMN such that BCMN = 54
Solution:
Analysis: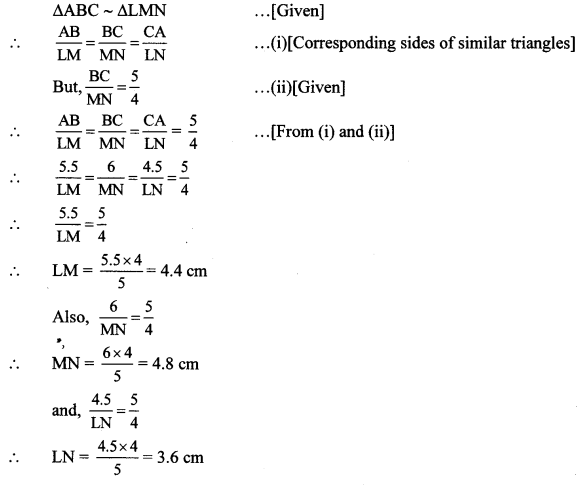

Question 2.
∆PQR ~ ∆LTR. In ∆PQR, PQ = 4.2 cm, QR = 5.4 cm, PR = 4.8 cm. Construct ∆PQR and ∆LTR, such that PQLT = 34
Solution:
Analysis:
As shown in the figure, Let R – P – L and R – Q – T.
∆PQR ~ ∆LTR … [Given]
∴ ∠PRQ ≅ ∠LRT … [Corresponding angles of similar triangles]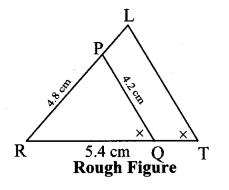

PQLT = QRTR = PRLR …(i)[Corresponding sides of similar triangles]
But, PQLT = 34 ….(ii) [Given]
∴ PQLT = QRTR = PRLR = 34 …[From (i) and (ii)]
∴ sides of LTR are longer than corresponding sides of ∆PQR.
If seg QR is divided into 3 equal parts, then seg TR will be 4 times each part of seg QR.
So, if we construct ∆PQR, point T will be on side RQ, at a distance equal to 4 parts from R.
Now, point L is the point of intersection of ray RP and a line through T, parallel to PQ.
∆LTR is the required triangle similar to ∆PQR.

Steps of construction:
i. Draw ∆PQR of given measure. Draw ray RS making an acute angle with side RQ.
ii. Taking convenient distance on the compass, mark 4 points R₁, R₂, R₃, and R₄, such that RR₁ = R₁R₂ = R₂R₃ = R₃R₄.
iii. Join R₃Q. Draw line parallel to R₃Q through R₄ to intersects ray RQ at T.
iv. Draw a line parallel to side PQ through T. Name the point of intersection of this line and ray RP as L.
∆LTR is the required triangle similar to ∆PQR.

Question 3.
∆RST ~ ∆XYZ. In ∆RST, RS = 4.5 cm, ∠RST = 40°, ST = 5.7 cm. Construct ∆RST and ∆XYZ, such that RSXY = 35.
Solution:
Analysis:
∆RST ~ ∆XYZ … [Given]
∴ ∠RST ≅ ∠XYZ = 40° … [Corresponding angles of similar triangles]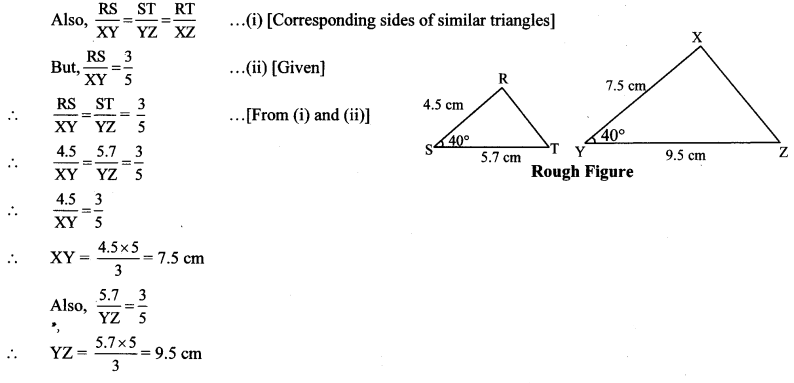

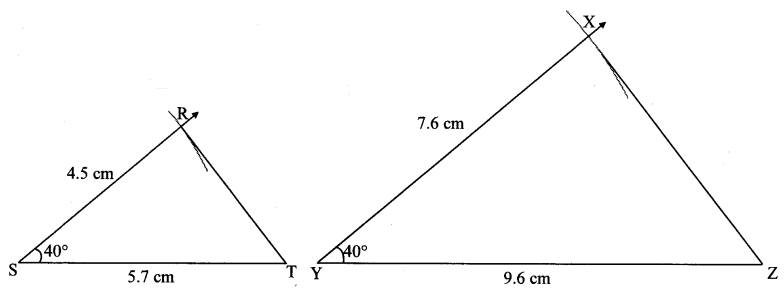
Question 4.
∆AMT ~ ∆ANE. In ∆AMT, AM = 6.3 cm, ∠TAM = 500, AT = 5.6 cm. AMAH = 75 Construct ∆AHE.
Solution:
Analysis:
As shown in the figure,
Let A – H – M and A – E – T.
∆AMT ~ ∆AHE … [Given]
∴ ∠TAM ≅ ∠EAH … [Corresponding angles of similar triangles]

AMAH = MTHE = ATAE ….. (i)[Corresponding sides of similar triangles]
But, AMAH = 75 …(ii)[Given]
∴ AMAH = MTHE = ATAH = 75 …[From (i) and (ii)]
∴ Sides of AAMT are longer than corresponding sides of ∆AHE.
∴ The length of side AH will be equal to 5 parts out of 7 equal parts of side AM.
So, if we construct AAMT, point H will be on side AM, at a distance equal to 5 parts from A.
Now, point E is the point of intersection of ray AT and a line through H, parallel to MT.
∆AHE is the required triangle similar to ∆AMT.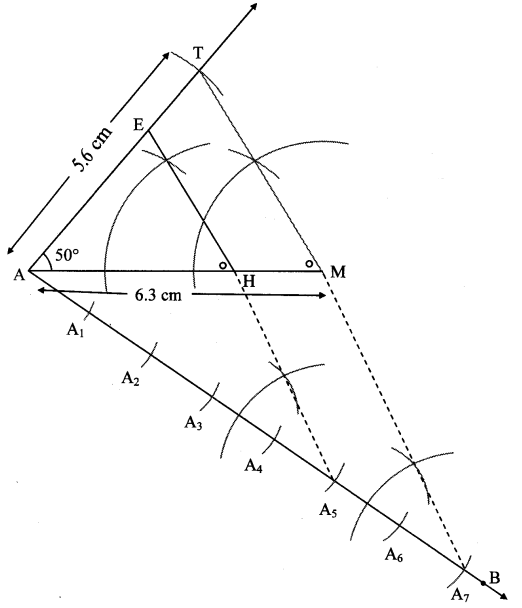

Steps of construction:
i. Draw ∆AMT of given measure. Draw ray AB making an acute angle with side AM.
ii. Taking convenient distance on the compass, mark 7 points A1, A2, A3, A4, A5, Ag and A7, such that
AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇.
iii. Join A₇M. Draw line parallel to A₇M through A₅ to intersects seg AM at H.
iv. Draw a line parallel to side TM through H. Name the point of intersection of this line and seg AT as E.
∆AHE is the required triangle similar to ∆AMT.

Question 1.
If length of side AB is 11.62 cm, then by dividing the line segment of length 11.6 cm in three equal parts, draw segment AB. (Textbook pg. no. 93)
Solution: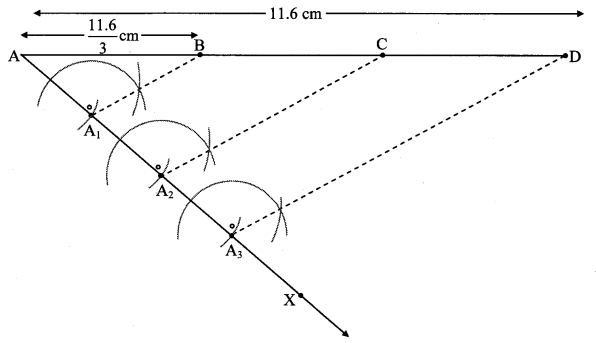

Steps of construction:
i. Draw seg AD of 11.6 cm.
ii. Draw ray AX such that ∠DAX is an acute angle.
iii. Locate points A₁, A₂ and A₃ on ray AX such that AA₁ = A₁A₂ = A₂A₃
iv. Join A₃D.
v. Through A₁, A₂ draw lines parallel to A₃D intersecting AD at B and C, wherein
AB = 11.63 cm

Question 2.
Construct any ∆ABC. Construct ∆ A’BC’ such that AB : A’B = 5:3 and ∆ ABC ~ ∆ A’BC’. (Textbook pg. no. 93)
Analysis:
As shown in the figure,
Let B – A’ – A and B – C’ -C
∆ ABC – A’BC’ … [Given]
∴ ∠ABC ≅ ∠A’BC’ …[Corresponding angles of similar trianglesi


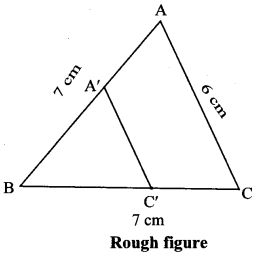
∴ Sides of ∆ABC are longer than corresponding sides of ∆A’BC’. Rough figure
∴ the length of side BC’ will be equal to 3 parts out of 5 equal parts of side BC.
So if we construct ∆ABC, point C’ will be on side BC, at a distance equal to 3 parts from B.
Now A’ is the point of intersection of AB and a line through C’, parallel to CA.
Solution:
Let ∆ABC be any triangle constructed such that AB = 7 cm, BC = 7 cm and AC = 6 cm.

Question 3.
Construct any ∆ABC. Construct ∆A’BC’ such that AB: A’B = 5:3 and ∆ABC ~ ∆A’BC’.
∆A’BC’ can also be constructed as shown in the adjoining figure. What changes do we have to make in steps of construction in that case? (Textbook pg. no. 94)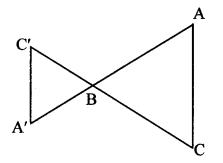

Solution:
Let ∆ABC be any triangle constructed such that AB = 5cm,
BC = 5.5 cm and AC = 6 cm.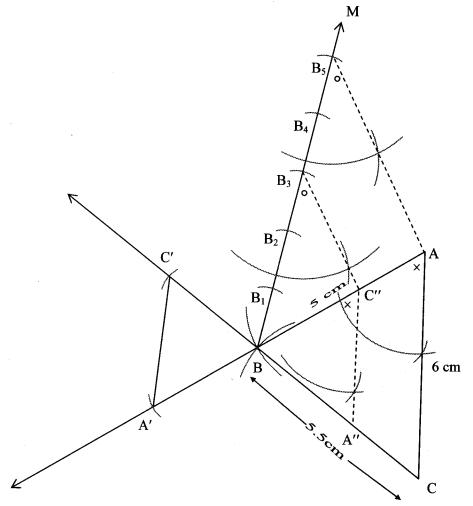

i. Steps of construction:
Construct ∆ABC, extend rays AB and CB.
Draw line BM making an acute angle with side AB.
Mark 5 points B₁, B₂, B₃, B₄, B₅ starting from B at equal distance.
Join B₃C” (ie 3rd part)
Draw a line parallel to AB₅ through B₃ to intersect line AB at C”
Draw a line parallel to AC through C” to intersect line BC at A”
ii. Extra construction:
With radius BC” cut an arc on extended ray CB at C’ [C’ – B – C]
With radius BA” cut an arc on extended ray AB at A’ [A’ – B – A]
∆A’BC’ is the required triangle.

Practice Set 4.2

Question 1.
Construct a tangent to a circle with centre P and radius 3.2 cm at any point M on it.
Solution:
Analysis:
seg PM ⊥ line l ….[Tangent is perpendicular to radius]

The perpendicular to seg PM at point M will give the required tangent at M.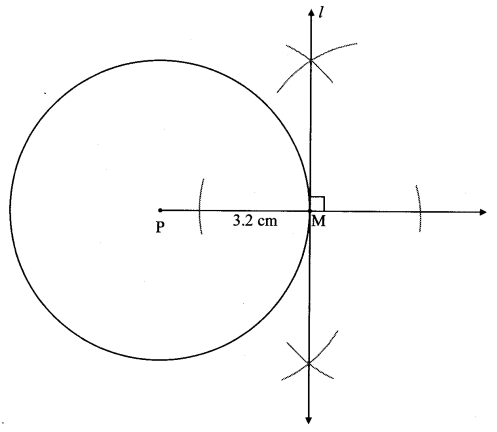

Question 2.
Draw a circle of radius 2.7 cm. Draw a tangent to the circle at any point on it.
Solution:
Analysis:
seg OM ⊥ line l …[Tangent is perpendicular to radius]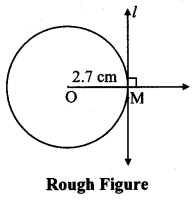

The perpendicular to seg OM at point M will give the required tangent at M.

Question 3.
Draw a circle of radius 3.6 cm. Draw a tangent to the circle at any point on it without using the centre.
Solution:
Analysis:
As shown in the figure, line lis a tangent to the circle at point K.
seg BK is a chord of the circle and LBAK is an inscribed angle.
By tangent secant angle theorem,
∠BAK = ∠BKR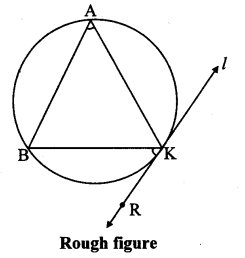

By converse of tangent secant angle theorem,
If we draw ∠BKR such that ∠BKR = ∠BAK, then ray KR
i.e. (line l) is a tangent at point K.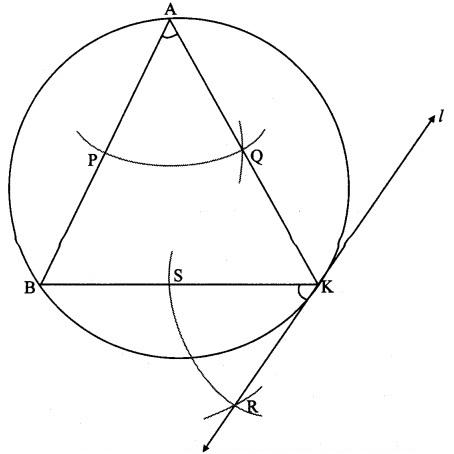

Question 4.
Draw a circle of radius 3.3 cm. Draw a chord PQ of length 6.6 cm. Draw tangents to the circle at points P and Q. Write your observation about the tangents.
Solution:
Analysis:
seg OP ⊥ line l …[Tangent is perpendicular to radius]
seg OQ ⊥ line m

The perpendicular to seg OP and seg OQ at points P and Q
respectively will give the required tangents at P and Q.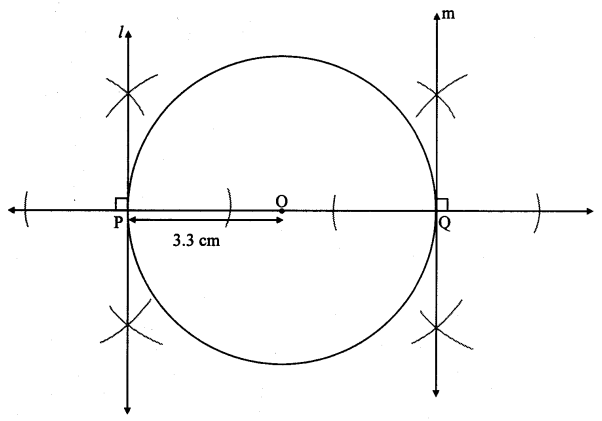

Radius = 3.3 cm
∴ Diameter = 2 × 3.3 = 6.6 cm
∴ Chord PQ is the diameter of the circle.
∴ The tangents through points P and Q (endpoints of diameter) are parallel to each other.

Question 5.
Draw a circle with radius 3.4 cm. Draw a chord MN of length 5.7 cm in it. Construct tangents at points M and N to the circle.
Solution:
Analysis:
seg ON ⊥ linel l
seg OM ⊥ Iine m …….[Tangent is perpendicular to radius]

The perpendicular to seg ON and seg 0M at points N and M respectively will give the required tangents at N and M.

Question 6.
Draw a circle with centre P and radius 3.4 cm. Take point Q at a distance 5.5 cm from the centre. Construct tangents to the circle from point Q.
Solution:
Analysis:
As shown in the figure, let Q be a point in the exterior of circle at a distance of 5.5 cm.
Let QR and QS be the tangents to the circle at points R and S respectively.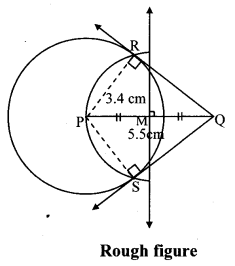

∴ seg PR ⊥ tangent QR …[Tangent is perpendicular to radius]
∴ ∠PRQ = 90°
∴ point R is on the circle having PQ as diameter. …[Angle inscribed in a semicircle is a right angle]
Similarly, point S also lies on the circle having PQ as diameter.
∴ Points R and S lie on the circle with PQ as diameter.
On drawing a circle with PQ as diameter, the points where it intersects the circle with centre P, will be the positions of points R and S respectively.
Ray QR and QS are the required tangents to the circle from point Q.

Question 7.
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Solution:
Analysis:
As shown in the figure, let Q be a point in the exterior of circle at a distance of 5.5 cm.
Let QR and QS be the tangents to the circle at points R and S respectively.
∴ seg PR ⊥ tangent QR …[Tangent is perpendicular to radius]
∴ ∠PRQ = 90°

∴ point R is on the circle having PQ as diameter. …[Angle inscribed in a semicircle is a right angle]
Similarly, point S also lies on the circle having PQ as diameter.
∴ Points R and S lie on the circle with PQ as diameter.
On drawing a circle with PQ as diameter, the points where it intersects the circle with centre P, will be the positions of points R and S respectively.
Ray QR and QS are the required tangents to the circle from point Q.

Download PDF

Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 4- Geometric Constructions

Download PDF: Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 4- Geometric Constructions PDF

Chapterwise Maharashtra Board Solutions Class 10 Maths (Part 2) :

• Chapter 1- Similarity
• Chapter 2- Pythagoras Theorem
• Chapter 3- Circle
• Chapter 4- Geometric Constructions
• Chapter 5- Co-ordinate Geometry
• Chapter 6- Trigonometry
• Chapter 7- Mensuration

FAQs

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC. 

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.

Read More

• NCERT Solutions for 10th Class Maths: Chapter 10 – Circles
• Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 3- Circle
• Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 1- Similarity
• Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 2- Pythagoras Theorem
• NCERT Solutions for 8th Class Maths: Chapter 9-Algebraic Expressions and Identities

IndCareer Board Book Solutions App

IndCareer Board Book App provides complete study materials for students from classes 1 to 12 of Board. The App contains complete solutions of NCERT books, notes, and other important materials for students. Download the IndCareer Board Book Solutions now.