Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 2- Pythagoras Theorem

Class 10: Maths Chapter 2 solutions. Complete Class 10 Maths Chapter 2 Notes.

Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 2- Pythagoras Theorem

Maharashtra Board 10th Maths Chapter 2, Class 10 Maths Chapter 2 solutions

Practice Set 2.1

Question 1.
Identify, with reason, which of the following are Pythagorean triplets.
i. (3,5,4)
ii. (4,9,12)
iii. (5,12,13)
iv. (24,70,74)
v. (10,24,27)
vi. (11,60,61)
Solution:
i. Here, 5² = 25
3² + 4² = 9 + 16 = 25
∴ 5² = 3² + 4²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (3,5,4) is a Pythagorean triplet.

ii. Here, 12² = 144
4² + 9²= 16 + 81 =97
∴ 12² ≠ 4² + 92
The square of the largest number is not equal to the sum of the squares of the other two numbers.
∴ (4,9,12) is not a Pythagorean triplet.

iii. Here, 13² = 169
5² + 12² = 25 + 144 = 169
∴ 13² = 5² + 12²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (5,12,13) is a Pythagorean triplet.

iv. Here, 74² = 5476
24² + 70² = 576 + 4900 = 5476
∴ 74² = 24² + 70²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (24, 70,74) is a Pythagorean triplet.

v. Here, 27² = 729
10² + 24² = 100 + 576 = 676
∴ 27² ≠ 10² + 24²
The square of the largest number is not equal to the sum of the squares of the other two numbers.
∴ (10,24,27) is not a Pythagorean triplet.

vi. Here, 61² = 3721
11² + 60² = 121 + 3600 = 3721
∴ 61² = 11² + 60²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (11,60,61) is a Pythagorean triplet.

Question 2.
In the adjoining figure, ∠MNP = 90°, seg NQ ⊥ seg MP,MQ = 9, QP = 4, find NQ.

Solution:
In ∆MNP, ∠MNP = 90° and [Given]
seg NQ ⊥ seg MP
NQ² = MQ × QP [Theorem of geometric mean]
∴ NQ = MQ×QP−−−−−−−−−√ [Taking square root of both sides]
= 9×4−−−−√
= 3 × 2
∴NQ = 6 units

Question 3.
In the adjoining figure, ∠QPR = 90°, seg PM ⊥ seg QR and Q – M – R, PM = 10, QM = 8, find QR.

Solution:
In ∆PQR, ∠QPR = 90° and [Given]
seg PM ⊥ seg QR
∴ PM² = OM × MR [Theorem of geometric mean]
∴ 10² = 8 × MR
∴ MR = 1008
= 12.5
Now, QR = QM + MR [Q – M – R]
= 8 + 12.5
∴ QR = 20.5 units

Question 4.
See adjoining figure. Find RP and PS using the information given in ∆PSR.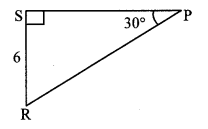

Solution:
In ∆PSR, ∠S = 90°, ∠P = 30° [Given]
∴ ∠R = 60° [Remaining angle of a triangle]
∴ ∆PSR is a 30° – 60° – 90° triangle.
RS = 12 RP [Side opposite to 30°]
∴6 = 12 RP
∴ RP = 6 × 2 = 12 units
Also, PS = 3√2 RP [Side opposite to 60°]
= 3√2 × 12
= 63–√ units
∴ RP = 12 units, PS = 6 3–√ units

Question 5.
For finding AB and BC with the help of information given in the adjoining figure, complete the following activity.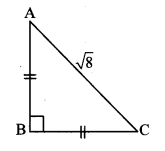

Solution:
AB = BC [Given]
∴ ∠BAC = ∠BCA [Isosceles triangle theorem]
Let ∠BAC = ∠BCA = x (i)
In ∆ABC, ∠A + ∠B + ∠C = 180° [Sum of the measures of the angles of a triangle is 180°]
∴ x + 90° + x = 180° [From (i)]
∴ 2x = 90°
∴ x = 90°2 [From (i)]
∴ x = 45°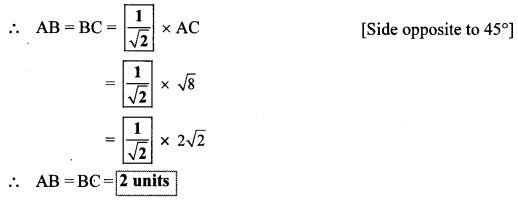

Question 6.
Find the side and perimeter of a square whose diagonal is 10 cm.

Solution:
Let ꠸ABCD be the given square.
l(diagonal AC) = 10 cm
Let the side of the square be ‘x’ cm.
In ∆ABC,
∠B = 90° [Angle of a square]
∴ AC² = AB² + BC² [Pythagoras theorem]
∴ 10² = x² + x²
∴ 100 = 2x²
∴ x² = 1002
∴x² = 50
∴ x = 50−−√ [Taking square root of both sides]
= =25×2−−−−−√=52–√
∴side of square is 52–√ cm.
= 4 × 5 2–√
∴ Perimeter of square = 20 2–√ cm

Question 7.
In the adjoining figure, ∠DFE = 90°, FG ⊥ ED. If GD = 8, FG = 12, find
i. EG
ii. FD, and
iii. EF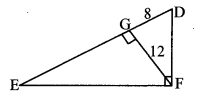

Solution:
i. In ∆DEF, ∠DFE = 90° and FG ⊥ ED [Given]
∴ FG² = GD × EG [Theorem of geometric mean]
∴ 122 = 8 × EG .
∴ EG = 1448
∴ EG = 18 units

ii. In ∆FGD, ∠FGD = 90° [Given]
∴ FD² = FG² + GD² [Pythagoras theorem]
= 122 + 82 = 144 + 64
= 208
∴ FD = 208−−−√ [Taking square root of both sides]
∴ FD = 4 13−−√ units

iii. In ∆EGF, ∠EGF = 90° [Given]
∴ EF² = EG² + FG² [Pythagoras theorem]
= 182 + 122 = 324 + 144
= 468
∴ EF = 468−−−√ [Taking square root of both sides]
∴ EF = 6 13−−√ units

Question 8.
Find the diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.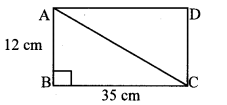

Solution:
Let ꠸ABCD be the given rectangle.
AB = 12 cm, BC 35 cm
In ∆ABC, ∠B = 90° [Angle of a rectangle]
∴ AC² = AB² + BC² [Pythagoras theorem]
= 122 + 352
= 144 + 1225
= 1369
∴ AC = 1369−−−−√ [Taking square root of both sides]
= 37 cm
∴ The diagonal of the rectangle is 37 cm.

Question 9.
In the adjoining figure, M is the midpoint of QR. ∠PRQ = 90°.
Prove that, PQ² = 4 PM² – 3 PR².

Solution:
Proof:
In ∆PQR, ∠PRQ = 90° [Given]
PQ² = PR² + QR² (i) [Pythagoras theorem]
RM = 12 QR [M is the midpoint of QR]
∴ 2RM = QR (ii)
∴ PQ² = PR² + (2RM)² [From (i) and (ii)]
∴ PQ² = PR² + 4RM² (iii)
Now, in ∆PRM, ∠PRM = 90° [Given]
∴ PM² = PR² + RM² [Pythagoras theorem]
∴ RM² = PM² – PR² (iv)
∴ PQ² = PR² + 4 (PM² – PR²) [From (iii) and (iv)]
∴ PQ² = PR² + 4 PM² – 4 PR²
∴ PQ² = 4 PM² – 3 PR²

Question 10.
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
Solution:
Let AC and CE represent the ladder of length 5.8 m, and A and E represent windows of the buildings on the opposite sides of the street. BD is the width of the street.

AB = 4 m and ED = 4.2 m
In ∆ABC, ∠B = 90° [Given]
AC² = AB² + BC² [Pythagoras theorem]
∴ 5.8² = 4² + BC²
∴ 5.8² – 4² = BC²
∴ (5.8 – 4) (5.8 + 4) = BC²
∴ 1.8 × 9.8 = BC²

CE² = CD² + DE² [Pythagoras theorem]
∴ 5.8² = CD² + 4.22
∴ 5.8² – 4.2² = CD²
∴ (5.8 – 4.2) (5.8 + 4.2) = CD²
∴ 1.6 × 10 = CD²
∴ CD² = 16
∴ CD = 4m (ii) [Taking square root of both sides]
Now, BD = BC + CD [B – C – D]
= 4.2 + 4 [From (i) and (ii)]
= 8.2 m
∴ The width of the street is 8.2 metres.

Question 1.
Verify that (3,4,5), (5,12,13), (8,15,17), (24,25,7) are Pythagorean triplets. (Textbook pg. no. 30)
Solution:
i. Here, 5² = 25
3² + 4² = 9 + 16 = 25
∴ 5² = 3² + 4²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 3,4,5 is a Pythagorean triplet.

ii. Here, 13² = 169
5² + 12² = 25 + 144 = 169
∴ 13² = 5² + 12²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 5,12,13 is a Pythagorean triplet.

iii. Here, 17² = 289
8² + 15² = 64 + 225 = 289
∴ 17² = 8² + 15²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 8,15,17 is a Pythagorean triplet.

iv. Here, 25² = 625
7² + 24² = 49 + 576 = 625
∴ 25² = 7² + 24²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 24,25, 7 is a Pythagorean triplet.

Question 2.
Assign different values to a and b and obtain 5 Pythagorean triplets. (Textbook pg. no. 31)
Solution:
i. Let a = 2, b = 1
a² + b² = 2² + 1² = 4 + 1 = 5
a² – b² = 2² – 1² = 4 – 1 = 3
2ab = 2 × 2 × 1 = 4
∴ (5, 3, 4) is a Pythagorean triplet.

ii. Let a = 4,b = 3
a² + b² = 4² + 3² = 16 + 9 = 25
a² – b² = 4² – 3² = 16 – 9 = 7
2ab = 2 × 4 × 3 = 24
∴ (25, 7, 24) is a Pythagorean triplet.

iii. Let a = 5, b = 2
a² + b² = 5² + 2² = 25 + 4 = 29
a² – b² = 5² – 2² = 25 – 4 = 21
2ab = 2 × 5 × 2 = 20
∴ (29, 21, 20) is a Pythagorean triplet.

iv. Let a = 4,b = 1
a² + b² = 4² + 1² = 16 + 1 = 17
a² – b² = 42 – 12 = 16 – 1 = 15
2ab = 2 × 4 × 1 = 8
∴ (17, 15, 8) is a Pythagorean triplet.

v. Let a = 9, b = 7
a² + b² = 92 + 72 = 81 + 49 = 130
a² – b² = 92 – 72 = 81 – 49 = 32
2ab = 2 × 9 × 7 = 126
∴ (130,32,126) is a Pythagorean triplet.

Note: Numbers in Pythagorean triplet can be written in any order.

Practice Set 2.2

Question 1.
In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.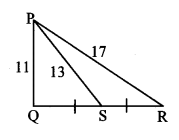

Solution:
In ∆PQR, point S is the midpoint of side QR. [Given]
∴ seg PS is the median.
∴ PQ² + PR² = 2 PS² + 2 SR² [Apollonius theorem]
∴ 11² + 17² = 2 (13)² + 2 SR²
∴ 121 + 289 = 2 (169)+ 2 SR²
∴ 410 = 338+ 2 SR²
∴ 2 SR² = 410 – 338
∴ 2 SR² = 72
∴ SR² = 722 = 36
∴ SR = 36−−√ [Taking square root of both sides]
= 6 units Now, QR = 2 SR [S is the midpoint of QR]
= 2 × 6
∴ QR = 12 units

Question 2.
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
Solution:
Let CD be the median drawn from the vertex C to side AB.
BD = 12 AB [D is the midpoint of AB]
= 12 × 10 = 5 units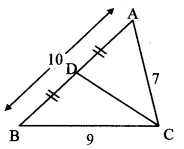

In ∆ABC, seg CD is the median. [Given]
∴ AC² + BC² = 2 CD² + 2 BD² [Apollonius theorem]
∴ 7² + 9² = 2 CD² + 2 (5)²
∴ 49 + 81 = 2 CD² + 2 (25)
∴ 130 = 2 CD² + 50
∴ 2 CD² = 130 – 50
∴ 2 CD² = 80
∴ CD² = 802 = 40
∴ CD = 40−−√ [Taking square root of both sides]
= 2 10−−√ units
∴ The length of the median drawn from point C to side AB is 2 10−−√ units.

Question 3.
In the adjoining figure, seg PS is the median of APQR and PT ⊥ QR. Prove that,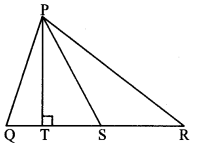

i. PR² = PS² + QR × ST + (QR2)²
ii. PQ² = PS² – QR × ST + (QR2)²
Solution:
i. QS = SR = 12 QR (i) [S is the midpoint of side QR]

∴ In ∆PSR, ∠PSR is an obtuse angle [Given]
and PT ⊥ SR [Given, Q-S-R]
∴ PR² = SR² +PS² + 2 SR × ST (ii) [Application of Pythagoras theorem]
∴ PR² = (12 QR)² + PS² + 2 (12 QR) × ST [From (i) and (ii)]
∴ PR² = (QR2)² + PS² + QR × ST
∴ PR² = PS² + QR × ST + (QR2)²

ii. In.∆PQS, ∠PSQ is an acute angle and [Given]

PT ⊥QS [Given, Q-S-R]
∴ PQ² = QS² + PS² – 2 QS × ST (iii) [Application of Pythagoras theorem]
∴ PR² = (12 QR)² + PS² – 2 (12 QR) × ST [From (i) and (iii)]
∴ PR² = (QR2)² + PS² – QR × ST
∴ PR² = PS² – QR × ST + (QR2)²

Question 4.
In ∆ABC, point M is the midpoint of side BC. If AB² + AC² = 290 cm, AM = 8 cm, find BC.

Solution:
In ∆ABC, point M is the midpoint of side BC. [Given]
∴ seg AM is the median.
∴ AB² + AC² = 2 AM² + 2 MC² [Apollonius theorem]
∴ 290 = 2 (8)² + 2 MC²
∴ 145 = 64 + MC² [Dividing both sides by 2]
∴ MC² = 145 – 64
∴ MC² = 81
∴ MC = 81−−√ [Taking square root of both sides]
MC = 9 cm
Now, BC = 2 MC [M is the midpoint of BC]
= 2 × 9
∴ BC = 18 cm

Question 5.
In the adjoining figure, point T is in the interior of rectangle PQRS. Prove that, TS² + TQ² = TP² + TR². (As shown in the figure, draw seg AB || side SR and A – T – B)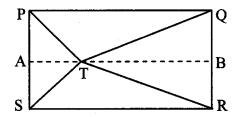

Given: ꠸PQRS is a rectangle.
Point T is in the interior of ꠸PQRS.
To prove: TS² + TQ² = TP² + TR²
Construction: Draw seg AB || side SR such that A – T – B.
Solution:
Proof:
꠸PQRS is a rectangle. [Given]
∴ PS = QR (i) [Opposite sides of a rectangle]
In ꠸ASRB,
∠S = ∠R = 90° (ii) [Angles of rectangle PQRS]
side AB || side SR [Construction]
Also ∠A = ∠S = 90° [Interior angle theorem, from (ii)]
∠B = ∠R = 90°
∴ ∠A = ∠B = ∠S = ∠R = 90° (iii)
∴ ꠸ASRB is a rectangle.
∴ AS = BR (iv) [Opposite sides of a rectanglel

In ∆PTS, ∠PST is an acute angle
and seg AT ⊥ side PS [From (iii)]
∴ TP² = PS² + TS² – 2 PS.AS (v) [Application of Pythagoras theorem]
In ∆TQR., ∠TRQ is an acute angle
and seg BT ⊥ side QR [From (iii)]
∴ TQ² = RQ² + TR² – 2 RQ.BR (vi) [Application of pythagoras theorem]

TP² – TQ² = PS² + TS² – 2PS.AS
-RQ² – TR² + 2RQ.BR [Subtracting (vi) from (v)]
∴ TP² – TQ² = TS² – TR² + PS²
– RQ² -2 PS.AS +2 RQ.BR
∴ TP² – TQ² = TS² – TR² + PS²
– PS² – 2 PS.BR + 2PS.BR [From (i) and (iv)]
∴ TP² – TQ² = TS² – TR²
∴ TS² + TQ² = TP² + TR²

Question 1.
In ∆ABC, ∠C is an acute angle, seg AD Iseg BC. Prove that: AB² = BC² + A² – 2 BC × DC. (Textbook pg. no. 44)
Given: ∠C is an acute angle, seg AD ⊥ seg BC.
To prove: AB² = BC² + AC² – 2BC × DC
Solution:
Proof:
∴ LetAB = c, AC = b, AD = p,

∴ BC = a, DC = x
BD + DC = BC [B – D – C]
∴ BD = BC – DC
∴ BD = a – x
In ∆ABD, ∠D = 90° [Given]
AB² = BD² + AD² [Pythagoras theorem]
∴ c² = (a – x)² + [P²] (i)
∴ c² = a² – 2ax + x² + [P²]
In ∆ADC, ∠D = 90° [Given]
AC² = AD² + CD² [Pythagoras theorem]
∴ b² = p² + [X²]
∴ p² = b² – [X²] (ii)
∴ c² = a² – 2ax + x² + b² – x² [Substituting (ii) in (i)]
∴ c² = a² + b² – 2ax
∴ AB² = BC² + AC² – 2 BC × DC

Question 2.
In ∆ABC, ∠ACB is an obtuse angle, seg AD ⊥ seg BC. Prove that: AB² = BC² + AC² + 2 BC × CD. (Textbook pg. no. 40 and 4.1)
Given: ∠ACB is an obtuse angle, seg AD ⊥ seg BC.
To prove: AB² = BC² + AC² + 2BC × CD
Solution:
Proof:

Let AD = p, AC = b, AB = c,
BC = a, DC = x
BD = BC + DC [B – C – D]
∴ BD = a + x
In ∆ADB, ∠D = 90° [Given]
AB² = BD² + AD² [Pythagoras theorem]
∴ c² = (a + x)² + p² (i)
∴ c² = a² + 2ax + x² + p²
Also, in ∆ADC, ∠D = 90° [Given]
AC² = CD² + AD² [Pythagoras theorem]
∴ b² = x² + p²
∴ p² = b² – x² (ii)
∴ c² = a² + 2ax + x² + b² – x² [Substituting (ii) in (i)]
∴ c² = a² + b² + 2ax
∴ AB² = BC² + AC² + 2 BC × CD

Question 3.
In ∆ABC, if M is the midpoint of side BC and seg AM ⊥seg BC, then prove that
AB² + AC² = 2 AM² + 2 BM². (Textbook pg, no. 41)
Given: In ∆ABC, M is the midpoint of side BC and seg AM ⊥ seg BC.
To prove: AB² + AC² = 2 AM² + 2 BM²
Solution:
Proof:

In ∆AMB, ∠M = 90° [segAM ⊥ segBC]
∴ AB2 = AM2 + BM2 (i) [Pythagoras theorem]
Also, in ∆AMC, ∠M = 90° [seg AM ⊥ seg BC]
∴ AC2 = AM2 + MC2 (ii) [Pythagoras theorem]
∴ AB² + AC² = AM² + BM² + AM² + MC² [Adding (i) and (ii)]
∴ AB² + AC² = 2 AM² + BM² + BM² [∵ BM = MC (M is the midpoint of BC)]
∴ AB² + AC² = 2 AM² + 2 BM²

Download PDF

Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 2- Pythagoras Theorem

Download PDF: Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 2- Pythagoras Theorem PDF

Chapterwise Maharashtra Board Solutions Class 10 Maths (Part 2) :

• Chapter 1- Similarity
• Chapter 2- Pythagoras Theorem
• Chapter 3- Circle
• Chapter 4- Geometric Constructions
• Chapter 5- Co-ordinate Geometry
• Chapter 6- Trigonometry
• Chapter 7- Mensuration

FAQs

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC. 

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.

Read More

• NCERT Solutions for Class 10th Mathematics: Chapter 6 – Triangles
• NCERT Solutions for 11th Class Maths: Chapter 8-Binomial Theorem
• RD Sharma Solutions for Class 12 Maths Chapter 15–Mean Value Theorems
• Maharashtra Board Solutions for Class 10-Maths (Part 2): Chapter 1- Similarity
• Bihar Board Syllabus Subject Wise Class 10th/12th

IndCareer Board Book Solutions App

IndCareer Board Book App provides complete study materials for students from classes 1 to 12 of Board. The App contains complete solutions of NCERT books, notes, and other important materials for students. Download the IndCareer Board Book Solutions now.