RD Sharma Solutions for Class 9 Maths Chapter 9–Triangle and its Angles

Class 9: Maths Chapter 9 solutions. Complete Class 9 Maths Chapter 9 Notes.

RD Sharma Solutions for Class 9 Maths Chapter 9–Triangle and its Angles

RD Sharma 9th Maths Chapter 9, Class 9 Maths Chapter 9 solutions

Exercise 9.1 Page No: 9.9

Question 1: In a ΔABC, if ∠A = 550, ∠B = 400, find ∠C.

Solution:

Given: ∠A = 550, ∠B = 400

We know, sum of all angles of a triangle is 1800

∠A + ∠B + ∠C = 1800

550 + 400 + ∠C=1800

950 + ∠C = 1800

∠C = 1800 − 950

∠C = 850

Question 2: If the angles of a triangle are in the ratio 1:2:3, determine three angles.

Solution:

Angles of a triangle are in the ratio 1:2:3 (Given)

Let the angles be x, 2x, 3x

Sum of all angles of triangles = 1800

x + 2x + 3x = 1800

6x = 1800

x = 1800/6

x = 300

Answer:

x = 300

2x = 2(30)0 = 600

3x = 3(30) 0 = 900

Question 3: The angles of a triangle are (x − 40)0, (x − 20) 0 and (1/2 x − 10) 0. Find the value of x.

Solution:

The angles of a triangle are (x − 40)0, (x − 20) 0 and (1/2 x − 10) 0

Sum of all angles of triangle = 1800

(x − 40)0 + (x − 20) 0 + (1/2 x − 10) 0 = 1800

5/2 x – 700 = 1800

5/2 x = 1800 + 700

5x = 2(250) 0

x = 5000/5

x = 1000

Question 4: The angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angles is 100, find the three angles.

Solution:

The difference between two consecutive angles is 100 (given)

Let x, x + 100, x + 200 be the consecutive angles

x + x + 100 + x + 200 = 1800

3x + 300 = 1800

3x = 1800– 300

3x = 1500

or x = 500

Again,

x + 100 = 500 + 100 = 600

x+200 = 500 + 200 = 700

Answer: Three angles are 500,600 and 700.

Question 5: Two angles of a triangle are equal and the third angle is greater than each of those angles by 300. Determine all the angles of the triangle.

Solution:

Two angles of a triangle are equal and the third angle is greater than each of those angles by 300. (Given)

Let x, x, x + 300 be the angles of a triangle.

Sum of all angles in a triangle = 1800

x + x + x + 300 = 1800

3x + 300 = 1800

3x = 1500

or x = 500

And x + 300 = 500 + 300 = 800

Answer: Three angles are 500, 500 and 800.

Question 6: If one angle of a triangle is equal to the sum of the other two, show that the triangle is a right angle triangle.

Solution:

One angle of a triangle is equal to the sum of the other two angles (given)

To Prove: One of the angles is 900

Let x, y and z are three angles of a triangle, where

z = x + y …(1)

Sum of all angles of a triangle = 1800

x + y + z = 1800

z + z = 1800 (Using equation (1))

2z = 1800

z = 900 (Proved)

Therefore, triangle is a right angled triangle.

Exercise 9.2 Page No: 9.18

Question 1: The exterior angles, obtained on producing the base of a triangle both ways are 1040 and 1360. Find all the angles of the triangle.

Solution:

∠ACD = ∠ABC + ∠BAC [Exterior angle property]

Find ∠ABC:

∠ABC + ∠ABE = 1800 [Linear pair]

∠ABC + 1360 = 1800

∠ABC = 440

Find ∠ACB:

∠ACB + ∠ACD = 1800 [Linear pair]

∠ACB + 1040 = 1800

∠ACB = 760

Now,

Sum of all angles of a triangle = 1800

∠A + 440 + 760 = 1800

∠A = 1800 − 440 −760

∠ A = 600

Answer: Angles of a triangle are ∠ A = 600, ∠B = 440 and ∠C = 760

Question 2: In a △ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q. Prove that ∠BPC + ∠BQC = 1800.

Solution:

In triangle ABC,

BP and CP are internal bisector of ∠B and ∠C respectively

=> External ∠B = 180o – ∠B

BQ and CQ are external bisector of ∠B and ∠C respectively.

=> External ∠C = 180 o – ∠C

In triangle BPC,

∠BPC + 1/2∠B + 1/2∠C = 180o

∠BPC = 180 o – 1/2(∠B + ∠C) …. (1)

In triangle BQC,

∠BQC + 1/2(180 o – ∠B) + 1/2(180 o – ∠C) = 180 o

∠BQC + 180 o – 1/2(∠B + ∠C) = 180 o

∠BPC + ∠BQC = 180 o [Using (1)]

Hence Proved.

Question 3: In figure, the sides BC, CA and AB of a △ABC have been produced to D, E and F respectively. If ∠ACD = 1050 and ∠EAF = 450, find all the angles of the △ABC.

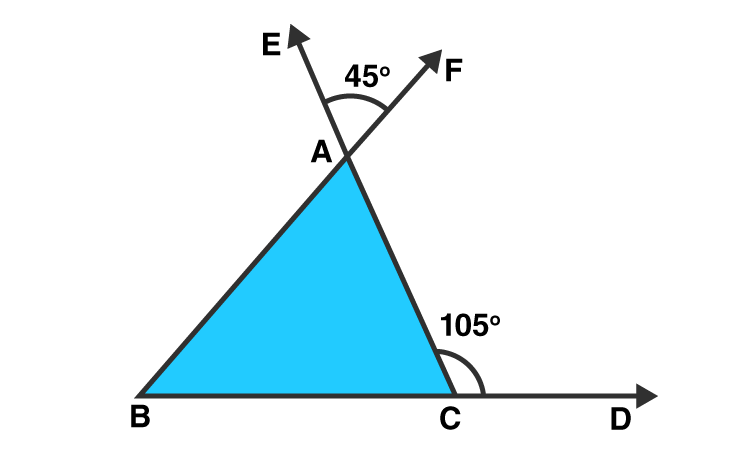
Solution:

∠BAC = ∠EAF = 450 [Vertically opposite angles]

∠ACD = 1800 – 1050 = 750 [Linear pair]

∠ABC = 1050 – 450 = 600 [Exterior angle property]

Question 4: Compute the value of x in each of the following figures:

(i)

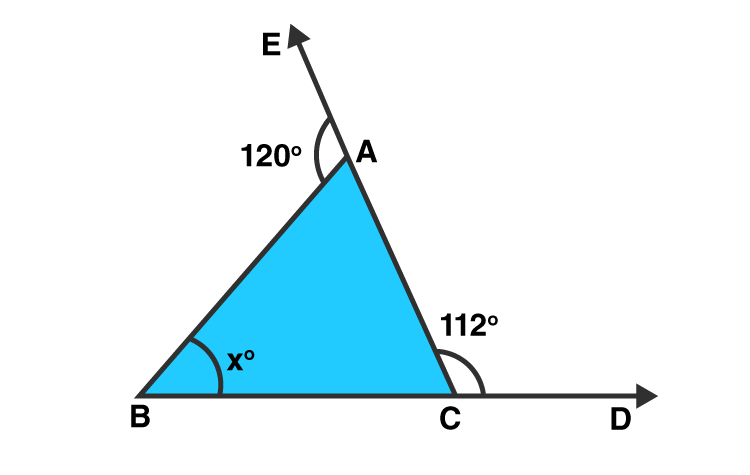
Solution:

∠BAC = 1800 – 1200 = 600 [Linear pair]

∠ACB = 1800 – 1120 = 680 [Linear pair]

Sum of all angles of a triangle = 1800

x = 1800 − ∠BAC − ∠ACB

= 1800 − 600 − 680 = 520

Answer: x = 520

(ii)

Solution:

∠ABC = 1800 – 1200 = 600 [Linear pair]

∠ACB = 1800 – 1100 = 700 [Linear pair]

Sum of all angles of a triangle = 1800

x = ∠BAC = 1800 − ∠ABC − ∠ACB

= 1800 – 600 – 700 = 500

Answer: x = 500

(iii)

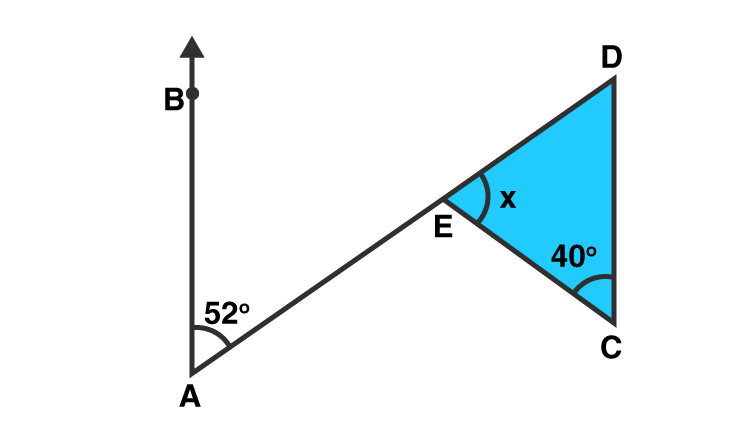
Solution:

∠BAE = ∠EDC = 520 [Alternate angles]

Sum of all angles of a triangle = 1800

x = 1800 – 400 – 520 = 1800 − 920 = 880

Answer: x = 880

(iv)

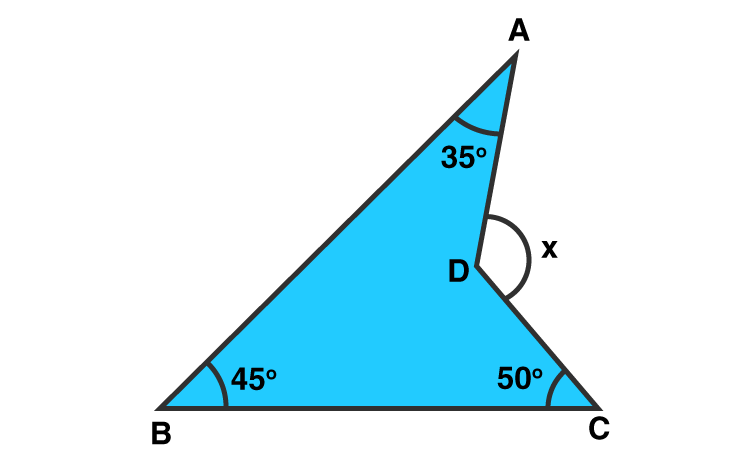
Solution:

CD is produced to meet AB at E.

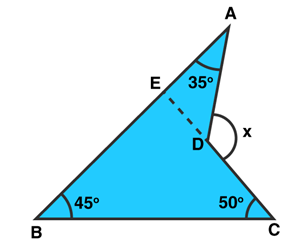
∠BEC = 1800 – 450 – 500 = 850 [Sum of all angles of a triangle = 1800]

∠AEC = 1800 – 850 = 950 [Linear Pair]

Now, x = 950 + 350 = 1300 [Exterior angle Property]

Answer: x = 1300

Question 5: In figure, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.

Solution:

∠DAC=180°−108°=72°

∠BAC/∠DAB​=1/3∠DAB=3∠BAC∠BAC+∠DAB=∠DAC=72°We can write it as∠BAC+3∠BAC=72°4∠BAC=72°∠BAC=72/4​=18°So we get∠DAB=3×18°=54°∠DAB=∠BDA=54°(AB=DB)∠ABD=180°−(54°+54°)=180−108°=72°Now,∠DBA=72°=∠BAC+x (Exterior angle)So we getx=72°−18°=54°

Exercise VSAQs Page No: 9.21

Question 1: Define a triangle.

Solution: Triangle is a three-sided polygon that consists of three edges and three vertices. The most important property of a triangle is that the sum of the internal angles of a triangle is equal to 180 degrees.

Question 2: Write the sum of the angles of an obtuse triangle.

Solution: The sum of angles of obtuse triangle = 180°.

Question 3: In △ABC, if ∠B = 600, ∠C = 800 and the bisectors of angles ∠ABC and ∠ACB meet at point O, then find the measure of ∠BOC.

Solution:

∠B = 600, ∠C = 800 (given)

As per question:

∠OBC = 600/2 = 300 and

∠OCB = 800/2 = 400

In triangle BOC,

∠OBC + ∠OCB + ∠BOC = 180 0[Sum of angles of a triangle = 1800]

300 + 400 + ∠BOC = 1800

∠BOC = 1100

Question 4: If the angles of a triangle are in the ratio 2:1:3, then find the measure of smallest angle.

Solution:

Let angles of a triangles are 2x, x and 3x, where x is the smallest angle.

To find: measure of x.

As, Sum of angles of a triangle = 1800

2x + x + 3x = 1800

6x = 1800

x = 300. Answer

Question 5: If the angles A, B and C of △ABC satisfy the relation B – A = C – B, then find the measure of ∠B.

Solution:

Sum of angles of a triangle = 1800

A + B + C = 1800 …(1)

B – A = C – B …(Given)

2B = C + A …(2)

(1) => 2B + B = 1800

3B =1800

Or B = 600

RD Sharma Solutions for Class 9 Maths Chapter 9: Download PDF

RD Sharma Solutions for Class 9 Maths Chapter 9–Triangle and its Angles

Download PDF: RD Sharma Solutions for Class 9 Maths Chapter 9–Triangle and its Angles PDF

Chapterwise RD Sharma Solutions for Class 9 Maths :

About RD Sharma

RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.

R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.

Read More