Class 11: Maths Chapter 22 solutions. Complete Class 11 Maths Chapter 22 Notes.
Contents
RD Sharma Solutions for Class 11 Maths Chapter 22–Brief review of Cartesian System of Rectangular Coordinates
RD Sharma 11th Maths Chapter 22, Class 11 Maths Chapter 22 solutions
EXERCISE 22.1 PAGE NO: 22.12
1. If the line segment joining the points P(x1, y1) and Q(x2, y2) subtends an angle α at the origin O, prove that : OP. OQ cos α = x1 x2 + y1 y2.
Solution:
Given,
Two points P and Q subtends an angle α at the origin as shown in figure:
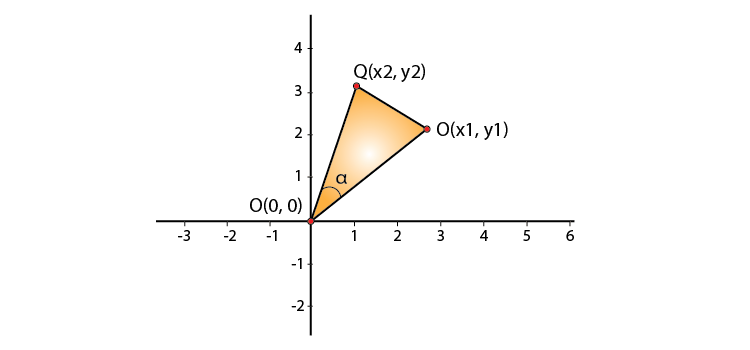
From figure we can see that points O, P and Q forms a triangle.
Clearly in ΔOPQ we have:

2. The vertices of a triangle ABC are A(0, 0), B (2, -1) and C (9, 0). Find cos B.
Solution:
Given:
The coordinates of triangle.
From the figure,

By using cosine formula,
In ΔABC, we have:
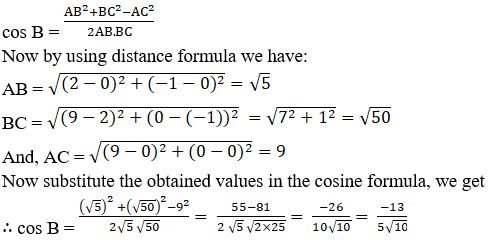
3. Four points A (6, 3), B (-3, 5), C (4, -2) and D (x, 3x) are given in such a way that , find x.
Solution:
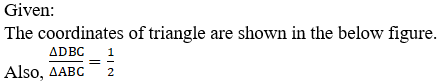
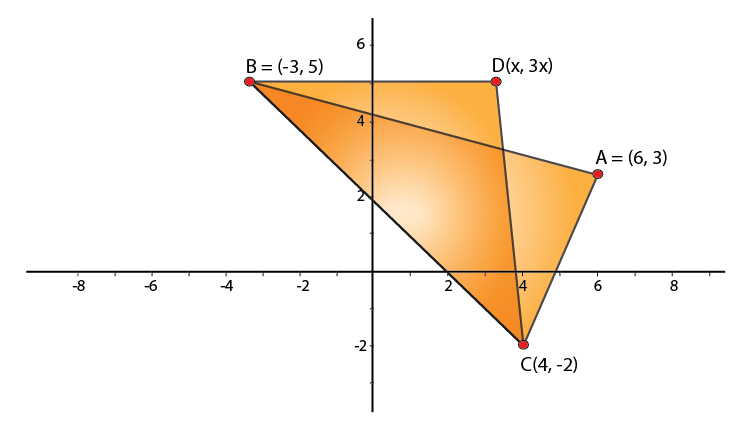

24.5 = 28x – 14
28x = 38.5
x = 38.5/28
= 1.375
4. The points A (2, 0), B (9, 1), C (11, 6) and D (4, 4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
Solution:
Given:
The coordinates of 4 points that form a quadrilateral is shown in the below figure
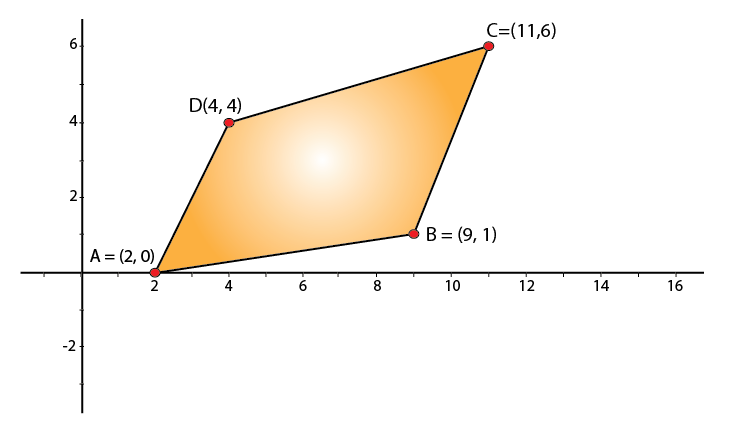
Now by using distance formula, we have:
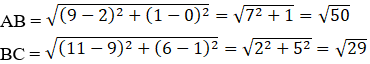
It is clear that, AB ≠ BC [quad ABCD does not have all 4 sides equal.]
∴ ABCD is not a Rhombus
EXERCISE 22.2 PAGE NO: 22.18
1. Find the locus of a point equidistant from the point (2, 4) and the y-axis.
Solution:
Let P (h, k) be any point on the locus and let A (2, 4) and B (0, k).
Then, PA = PB
PA2 = PB2

2. Find the equation of the locus of a point which moves such that the ratio of its distance from (2, 0) and (1, 3) is 5: 4.
Solution:
Let P (h, k) be any point on the locus and let A (2, 0) and B (1, 3).
So then, PA/ BP = 5/4
PA2 = BP2 = 25/16


3. A point moves as so that the difference of its distances from (ae, 0) and (-ae, 0) is 2a, prove that the equation to its locus is
, where b2 = a2 (e2 – 1).
Solution:
Let P (h, k) be any point on the locus and let A (ae, 0) and B (-ae, 0).
Where, PA – PB = 2a

Now again let us square on both the sides we get,
(eh + a)2 = (h + ae)2 + (k – 0)2
e2h2 + a2 + 2aeh = h2 + a2e2 + 2aeh + k2
h2 (e2 – 1) – k2 = a2 (e2 – 1)
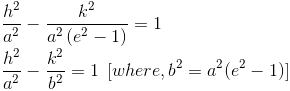
Now let us replace (h, k) with (x, y)
The locus of a point such that the difference of its distances from (ae, 0) and (-ae, 0) is 2a.
Where b2 = a2 (e2 – 1)
Hence proved.
4. Find the locus of a point such that the sum of its distances from (0, 2) and (0, -2) is 6.
Solution:
Let P (h, k) be any point on the locus and let A (0, 2) and B (0, -2).
Where, PA – PB = 6


5. Find the locus of a point which is equidistant from (1, 3) and x-axis.
Solution:
Let P (h, k) be any point on the locus and let A (1, 3) and B (h, 0).
Where, PA = PB

6. Find the locus of a point which moves such that its distance from the origin is three times is distance from x-axis.
Solution:
Let P (h, k) be any point on the locus and let A (0, 0) and B (h, 0).
Where, PA = 3PB

Now by squaring on both the sides we get,
h2 + k2 = 9k2
h2 = 8k2
By replacing (h, k) with (x, y)
∴ The locus of point is x2 = 8y2
EXERCISE 22.3 PAGE NO: 22.21
1. What does the equation (x – a) 2 + (y – b) 2 = r2 become when the axes are transferred to parallel axes through the point (a-c, b)?
Solution:
Given:
The equation, (x – a) 2 + (y – b) 2 = r2
The given equation (x – a)2 + (y – b)2 = r2 can be transformed into the new equation by changing x by x – a + c and y by y – b, i.e. substitution of x by x + a and y by y + b.
((x + a – c) – a)2 + ((y – b ) – b)2 = r2
(x – c)2 + y2 = r2
x2 + c2 – 2cx + y2 = r2
x2 + y2 -2cx = r2 – c2
Hence, the transformed equation is x2 + y2 -2cx = r2 – c2
2. What does the equation (a – b) (x2 + y2) – 2abx = 0 become if the origin is shifted to the point (ab / (a-b), 0) without rotation?
Solution:
Given:
The equation (a – b) (x2 + y2) – 2abx = 0
The given equation (a – b) (x2 + y2) – 2abx = 0 can be transformed into new equation by changing x by [X + ab / (a-b)] and y by Y

3. Find what the following equations become when the origin is shifted to the point (1, 1)?
(i) x2 + xy – 3x – y + 2 = 0
(ii) x2 – y2 – 2x + 2y = 0
(iii) xy – x – y + 1 = 0
(iv) xy – y2 – x + y = 0
Solution:
(i) x2 + xy – 3x – y + 2 = 0
Firstly let us substitute the value of x by x + 1 and y by y + 1
Then,
(x + 1)2 + (x + 1) (y + 1) – 3(x + 1) – (y + 1) + 2 = 0
x2 + 1 + 2x + xy + x + y + 1 – 3x – 3 – y – 1 + 2 = 0
Upon simplification we get,
x2 + xy = 0
∴ The transformed equation is x2 + xy = 0.
(ii) x2 – y2 – 2x + 2y = 0
Let us substitute the value of x by x + 1 and y by y + 1
Then,
(x + 1)2 – (y + 1)2 – 2(x + 1) + 2(y + 1) = 0
x2 + 1 + 2x – y2 – 1 – 2y – 2x – 2 + 2y + 2 = 0
Upon simplification we get,
x2 – y2 = 0
∴ The transformed equation is x2 – y2 = 0.
(iii) xy – x – y + 1 = 0
Let us substitute the value of x by x + 1 and y by y + 1
Then,
(x + 1) (y + 1) – (x + 1) – (y + 1) + 1 = 0
xy + x + y + 1 – x – 1 – y – 1 + 1 = 0
Upon simplification we get,
xy = 0
∴ The transformed equation is xy = 0.
(iv) xy – y2 – x + y = 0
Let us substitute the value of x by x + 1 and y by y + 1
Then,
(x + 1) (y + 1) – (y + 1)2 – (x + 1) + (y + 1) = 0
xy + x + y + 1 – y2 – 1 – 2y – x – 1 + y + 1 = 0
Upon simplification we get,
xy – y2 = 0
∴ The transformed equation is xy – y2 = 0.
4. At what point the origin be shifted so that the equation x2 + xy – 3x + 2 = 0 does not contain any first-degree term and constant term?
Solution:
Given:
The equation x2 + xy – 3x + 2 = 0
We know that the origin has been shifted from (0, 0) to (p, q)
So any arbitrary point (x, y) will also be converted as (x + p, y + q).
The new equation is:
(x + p)2 + (x + p)(y + q) – 3(x + p) + 2 = 0
Upon simplification,
x2 + p2 + 2px + xy + py + qx + pq – 3x – 3p + 2 = 0
x2 + xy + x(2p + q – 3) + y(q – 1) + p2 + pq – 3p – q + 2 = 0
For no first degree term, we have 2p + q – 3 = 0 and p – 1 = 0, and
For no constant term we have p2 + pq – 3p – q + 2 = 0.
By solving these simultaneous equations we have p = 1 and q = 1 from first equation.
The values p = 1 and q = 1 satisfies p2 + pq – 3p – q + 2 = 0.
Hence, the point to which origin must be shifted is (p, q) = (1, 1).
5. Verify that the area of the triangle with vertices (2, 3), (5, 7) and (-3 -1) remains invariant under the translation of axes when the origin is shifted to the point (-1, 3).
Solution:
Given:
The points (2, 3), (5, 7), and (-3, -1).
The area of triangle with vertices (x1, y1), (x2, y2), and (x3, y3) is
= ½ [x1(y2 – y3) + x2(y3 -y1) + x3(y1 – y2)]
The area of given triangle = ½ [2(7+1) + 5(-1-3) – 3(3-7)]
= ½ [16 – 20 + 12]
= ½ [8]
= 4
Origin shifted to point (-1, 3), the new coordinates of the triangle are (3, 0), (6, 4), and (-2, -4) obtained from subtracting a point (-1, 3).
The new area of triangle = ½ [3(4-(-4)) + 6(-4-0) – 2(0-4)]
= ½ [24-24+8]
= ½ [8]
= 4
Since the area of the triangle before and after the translation after shifting of origin remains same, i.e. 4.
∴ We can say that the area of a triangle is invariant to shifting of origin.
RD Sharma Solutions for Class 11 Maths Chapter 22: Download PDF
RD Sharma Solutions for Class 11 Maths Chapter 22–Brief review of Cartesian System of Rectangular Coordinates
Chapterwise RD Sharma Solutions for Class 11 Maths :
- Chapter 1–Sets
- Chapter 2–Relations
- Chapter 3–Functions
- Chapter 4–Measurement of Angles
- Chapter 5–Trigonometric Functions
- Chapter 6–Graphs of Trigonometric Functions
- Chapter 7–Values of Trigonometric Functions at Sum or Difference of Angles
- Chapter 8–Transformation Formulae
- Chapter 9–Values of Trigonometric Functions at Multiples and Submultiples of an Angle
- Chapter 10–Sine and Cosine Formulae and their Applications
- Chapter 11–Trigonometric Equations
- Chapter 12–Mathematical Induction
- Chapter 13–Complex Numbers
- Chapter 14–Quadratic Equations
- Chapter 15–Linear Inequations
- Chapter 16–Permutations
- Chapter 17–Combinations
- Chapter 18–Binomial Theorem
- Chapter 19–Arithmetic Progressions
- Chapter 20–Geometric Progressions
- Chapter 21–Some Special Series
- Chapter 22–Brief review of Cartesian System of Rectangular Coordinates
- Chapter 23–The Straight Lines
- Chapter 24–The Circle
- Chapter 25–Parabola
- Chapter 26–Ellipse
- Chapter 27–Hyperbola
- Chapter 28–Introduction to Three Dimensional Coordinate Geometry
- Chapter 29–Limits
- Chapter 30–Derivatives
- Chapter 31–Mathematical Reasoning
- Chapter 32–Statistics
- Chapter 33–Probability
About RD Sharma
RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.
R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.
