RD Sharma Solutions for Class 11 Maths Chapter 15–Linear Inequations
RD Sharma Solutions for Class 11 Maths Chapter 15–Linear Inequations

Class 11: Maths Chapter 15 solutions. Complete Class 11 Maths Chapter 15 Notes.

RD Sharma Solutions for Class 11 Maths Chapter 15–Linear Inequations

RD Sharma 11th Maths Chapter 15, Class 11 Maths Chapter 15 solutions

EXERCISE 15.1 PAGE NO: 15.10

Solve the following linear Inequations in R.

1. Solve: 12x < 50, when

(i) x ∈ R

(ii) x ∈ Z

(iii) x ∈ N

Solution:

Given:

12x < 50

So when we divide by 12, we get

12x/ 12 < 50/12

x < 25/6

(i) x ∈ R

When x is a real number, the solution of the given inequation is (-∞, 25/6).

(ii) x ∈ Z

When, 4 < 25/6 < 5

So when, when x is an integer, the maximum possible value of x is 4.

The solution of the given inequation is {…, –2, –1, 0, 1, 2, 3, 4}.

(iii) x ∈ N

When, 4 < 25/6 < 5

So when, when x is a natural number, the maximum possible value of x is 4. We know that the natural numbers start from 1, the solution of the given inequation is {1, 2, 3, 4}.

2. Solve: -4x > 30, when

(i) x ∈ R

(ii) x ∈ Z

(iii) x ∈ N

Solution:

Given:

-4x > 30

So when we divide by 4, we get

-4x/4 > 30/4

-x > 15/2

x < – 15/2

(i) x ∈ R

When x is a real number, the solution of the given inequation is (-∞, -15/2).

(ii) x ∈ Z

When, -8 < -15/2 < -7

So when, when x is an integer, the maximum possible value of x is -8.

The solution of the given inequation is {…, –11, –10, -9, -8}.

(iii) x ∈ N

As natural numbers start from 1 and can never be negative, when x is a natural number, the solution of the given inequation is ∅.

3. Solve: 4x-2 < 8, when

(i) x ∈ R

(ii) x ∈ Z

(iii) x ∈ N

Solution:

Given:

4x – 2 < 8

4x – 2 + 2 < 8 + 2

4x < 10

So divide by 4 on both sides we get,

4x/4 < 10/4

x < 5/2

(i) x ∈ R

When x is a real number, the solution of the given inequation is (-∞, 5/2).

(ii) x ∈ Z

When, 2 < 5/2 < 3

So when, when x is an integer, the maximum possible value of x is 2.

The solution of the given inequation is {…, –2, –1, 0, 1, 2}.

(iii) x ∈ N

When, 2 < 5/2 < 3

So when, when x is a natural number, the maximum possible value of x is 2. We know that the natural numbers start from 1, the solution of the given inequation is {1, 2}.

4. 3x – 7 > x + 1

Solution:

Given:

3x – 7 > x + 1

3x – 7 + 7 > x + 1 + 7

3x > x + 8

3x – x > x + 8 – x

2x > 8

Divide both sides by 2, we get

2x/2 > 8/2

x > 4

∴ The solution of the given inequation is (4, ∞).

5. x + 5 > 4x – 10

Solution:

Given: x + 5 > 4x – 10

x + 5 – 5 > 4x – 10 – 5

x > 4x – 15

4x – 15 < x

4x – 15 – x < x – x

3x – 15 < 0

3x – 15 + 15 < 0 + 15

3x < 15

Divide both sides by 3, we get

3x/3 < 15/3

x < 5

∴ The solution of the given inequation is (-∞, 5).

6. 3x + 9 ≥ –x + 19

Solution:

Given: 3x + 9 ≥ –x + 19

3x + 9 – 9 ≥ –x + 19 – 9

3x ≥ –x + 10

3x + x ≥ –x + 10 + x

4x ≥ 10

Divide both sides by 4, we get

4x/4 ≥ 10/4

x ≥ 5/2

∴ The solution of the given inequation is [5/2, ∞).

7. 2 (3 – x) ≥ x/5 + 4

Solution:

Given: 2 (3 – x) ≥ x/5 + 4

6 – 2x ≥ x/5 + 4

6 – 2x ≥ (x+20)/5

5(6 – 2x) ≥ (x + 20)

30 – 10x ≥ x + 20

30 – 20 ≥ x + 10x

10 ≥11x

11x ≤ 10

Divide both sides by 11, we get

11x/11 ≤ 10/11

x ≤ 10/11

∴ The solution of the given inequation is (-∞, 10/11].

8. (3x – 2)/5 ≤ (4x – 3)/2

Solution:

Given:

(3x – 2)/5 ≤ (4x – 3)/2

Multiply both the sides by 5 we get,

(3x – 2)/5 × 5 ≤ (4x – 3)/2 × 5

(3x – 2) ≤ 5(4x – 3)/2

3x – 2 ≤ (20x – 15)/2

Multiply both the sides by 2 we get,

(3x – 2) × 2 ≤ (20x – 15)/2 × 2

6x – 4 ≤ 20x – 15

20x – 15 ≥ 6x – 4

20x – 15 + 15 ≥ 6x – 4 + 15

20x ≥ 6x + 11

20x – 6x ≥ 6x + 11 – 6x

14x ≥ 11

Divide both sides by 14, we get

14x/14 ≥ 11/14

x ≥ 11/14

∴ The solution of the given inequation is [11/14, ∞).

9. –(x – 3) + 4 < 5 – 2x

Solution:

Given: –(x – 3) + 4 < 5 – 2x

–x + 3 + 4 < 5 – 2x

–x + 7 < 5 – 2x

–x + 7 – 7 < 5 – 2x – 7

–x < –2x – 2

–x + 2x < –2x – 2 + 2x

x < –2

∴ The solution of the given inequation is (–∞, –2).

10. x/5 < (3x-2)/4 – (5x-3)/5

Solution:

Given: x/5 < (3x-2)/4 – (5x-3)/5

x/5 < [5(3x-2) – 4(5x-3)]/4(5)

x/5 < [15x – 10 – 20x + 12]/20

x/5 < [2 – 5x]/20

Multiply both the sides by 20 we get,

x/5 × 20 < [2 – 5x]/20 × 20

4x < 2 – 5x

4x + 5x < 2 – 5x + 5x

9x < 2

Divide both sides by 9, we get

9x/9 < 2/9

x < 2/9

∴ The solution of the given inequation is (-∞, 2/9).

11. [2(x-1)]/5 ≤ [3(2+x)]/7

Solution:

Given:[2(x-1)]/5 ≤ [3(2+x)]/7

(2x – 2)/5 ≤ (6 + 3x)/7

Multiply both the sides by 5 we get,

(2x – 2)/5 × 5 ≤ (6 + 3x)/7 × 5

2x – 2 ≤ 5(6 + 3x)/7

7 (2x – 2) ≤ 5 (6 + 3x)

14x – 14 ≤ 30 + 15x

14x – 14 + 14 ≤ 30 + 15x + 14

14x ≤ 44 + 15x

14x – 44 ≤ 44 + 15x – 44

14x – 44 ≤ 15x

15x ≥ 14x – 44

15x – 14x ≥ 14x – 44 – 14x

x ≥ –44

∴ The solution of the given inequation is [–44, ∞).

12. 5x/2 + 3x/4 ≥ 39/4

Solution:

Given:

5x/2 + 3x/4 ≥ 39/4

By taking LCM[2(5x)+3x]/4 ≥ 39/4

13x/4 ≥ 39/4

Multiply both the sides by 4 we get,

13x/4 × 4 ≥ 39/4 × 4

13x ≥ 39

Divide both sides by 13, we get

13x/13 ≥ 39/13

x ≥ 39/13

x ≥ 3

∴ The solution of the given inequation is [3, ∞).

13. (x – 1)/3 + 4 < (x – 5)/5 – 2

Solution:

Given:

(x – 1)/3 + 4 < (x – 5)/5 – 2

Subtract both sides by 4 we get,

(x – 1)/3 + 4 – 4 < (x – 5)/5 – 2 – 4

(x – 1)/3 < (x – 5)/5 – 6

(x – 1)/3 < (x – 5 – 30)/5

(x – 1)/3 < (x – 35)/5

Cross multiply we get,

5 (x – 1) < 3 (x – 35)

5x – 5 < 3x – 105

5x – 5 + 5 < 3x – 105 + 5

5x < 3x – 100

5x – 3x < 3x – 100 – 3x

2x < –100

Divide both sides by 2, we get

2x/2 < -100/2

x < -50

∴ The solution of the given inequation is (-∞, -50).

14. (2x + 3)/4 – 3 < (x – 4)/3 – 2

Solution:

Given:

(2x + 3)/4 – 3 < (x – 4)/3 – 2

Add 3 on both sides we get,

(2x + 3)/4 – 3 + 3 < (x – 4)/3 – 2 + 3

(2x + 3)/4 < (x – 4)/3 + 1

(2x + 3)/4 < (x – 4 + 3)/3

(2x + 3)/4 < (x – 1)/3

Cross multiply we get,

3 (2x + 3) < 4 (x – 1)

6x + 9 < 4x – 4

6x + 9 – 9 < 4x – 4 – 9

6x < 4x – 13

6x – 4x < 4x – 13 – 4x

2x < –13

Divide both sides by 2, we get

2x/2 < -13/2

x < -13/2

∴ The solution of the given inequation is (-∞, -13/2).

EXERCISE 15.2 PAGE NO: 15.15

Solve each of the following system of equations in R.

1. x + 3 > 0, 2x < 14

Solution:

Given: x + 3 > 0 and 2x < 14

Let us consider the first inequality.

x + 3 > 0

x + 3 – 3 > 0 – 3

x > –3

Now, let us consider the second inequality.

2x < 14

Divide both the sides by 2 we get,

2x/2 < 14/2

x < 7

∴ The solution of the given system of inequation is (–3, 7).

2. 2x – 7 > 5 – x, 11 – 5x ≤ 1

Solution:

Given:

2x – 7 > 5 – x and 11 – 5x ≤ 1

Let us consider the first inequality.

2x – 7 > 5 – x

2x – 7 + 7 > 5 – x + 7

2x > 12 – x

2x + x > 12 – x + x

3x > 12

Divide both the sides by 3 we get,

3x/3 > 12/3

x > 4

∴ x ∈ ( 4, ∞) … (1)

Now, let us consider the second inequality.

11 – 5x ≤ 1

11 – 5x – 11 ≤ 1 – 11

–5x ≤ –10

Divide both the sides by 5 we get,

-5x/5 ≤ -10/5

–x ≤ –2

x ≥ 2

∴ x ∈ [2, ∞) … (2)

From (1) and (2) we get

x ∈ (4, ∞) ∩ [2, ∞)

x ∈ (4, ∞)

∴ The solution of the given system of inequations is (4, ∞).

3. x – 2 > 0, 3x < 18

Solution:

Given:

x – 2 > 0 and 3x < 18

Let us consider the first inequality.

x – 2 > 0

x – 2 + 2 > 0 + 2

x > 2

∴ x ∈ ( 2, ∞) …(1)

Now, let us consider the second inequality.

3x < 18

Divide both the sides by 3 we get,

3x/3 < 18/3

x < 6

∴ x ∈ (–∞, 6) …(2)

From (1) and (2), we get

x ∈ (2, ∞) ∩ (–∞, 6)

x ∈ ( 2, 6)

∴ The solution of the given system of inequations is (2, 6).

4. 2x + 6 ≥ 0, 4x – 7 < 0

Solution:

Given:

2x + 6 ≥ 0 and 4x – 7 < 0

Let us consider the first inequality.

2x + 6 ≥ 0

2x + 6 – 6 ≥ 0 – 6

2x ≥ –6

Divide both the sides by 2 we get,

2x/2 ≥ -6/2

x ≥ -3

∴ x ∈ [–3, ∞) …(1)

Now, let us consider the second inequality.

4x – 7 < 0

4x – 7 + 7 < 0 + 7

4x < 7

Divide both the sides by 4 we get,

4x/4 < 7/4

x < 7/4

∴ x ∈ [–∞, 7/4) …(2)

From (1) and (2), we get

x ∈ [-3, ∞) ∩ (–∞, 7/4)

x ∈ [-3, 7/4)

∴ The solution of the given system of inequations is [-3, 7/4).

5. 3x – 6 > 0, 2x – 5 > 0

Solution:

Given:

3x – 6 > 0 and 2x – 5 > 0

Let us consider the first inequality.

3x – 6 > 0

3x – 6 + 6 > 0 + 6

3x > 6

Divide both the sides by 3 we get,

3x/3 > 6/3

x > 2

∴ x ∈ ( 2, ∞)… (1)

Now, let us consider the second inequality.

2x – 5 > 0

2x – 5 + 5 > 0 + 5

2x > 5

Divide both the sides by 2 we get,

2x/2 > 5/2

x > 5/2

∴ x ∈ (5/2, ∞)… (2)

From (1) and (2), we get

x ∈ (2, ∞) ∩ (5/2, ∞)

x ∈ (5/2, ∞)

∴ The solution of the given system of inequations is (5/2, ∞).

6. 2x – 3 < 7, 2x > –4

Solution:

Given:

2x – 3 < 7 and 2x > –4

Let us consider the first inequality.

2x – 3 < 7

2x – 3 + 3 < 7 + 3

2x < 10

Divide both the sides by 2 we get,

2x/2 < 10/2

x < 5

∴ x ∈ ( –∞, 5)… (1)

Now, let us consider the second inequality.

2x > –4

Divide both the sides by 2 we get,

2x/2 > -4/2

x > –2

∴ x ∈ (–2, ∞)… (2)

From (1) and (2), we get

x ∈ (–∞, 5) ∩ (–2, ∞)

x ∈ (–2, 5)

∴ The solution of the given system of inequations is (–2, 5).

7. 2x + 5 ≤ 0, x – 3 ≤ 0

Solution:

Given:

2x + 5 ≤ 0 and x – 3 ≤ 0

Let us consider the first inequality.

2x + 5 ≤ 0

2x + 5 – 5 ≤ 0 – 5

2x ≤ –5

Divide both the sides by 2 we get,

2x/2 ≤ –5/2

x ≤ – 5/2

∴ x ∈ (–∞, -5/2]… (1)

Now, let us consider the second inequality.

x – 3 ≤ 0

x – 3 + 3 ≤ 0 + 3

x ≤ 3

∴ x ∈ (–∞, 3]… (2)

From (1) and (2), we get

x ∈ (–∞, -5/2] ∩ (–∞, 3)

x ∈ (–∞, -5/2]

∴ The solution of the given system of inequations is (–∞, -5/2].

8. 5x – 1 < 24, 5x + 1 > –24

Solution:

Given:

5x – 1 < 24 and 5x + 1 > –24

Let us consider the first inequality.

5x – 1 < 24

5x – 1 + 1 < 24 + 1

5x < 25

Divide both the sides by 5 we get,

5x/5 < 25/5

x < 5

∴ x ∈ (–∞, 5)… (1)

Now, let us consider the second inequality.

5x + 1 > –24

5x + 1 – 1 > –24 – 1

5x > –25

Divide both the sides by 5 we get,

5x/5 > -25/5

x > -5

∴ x ∈ (–5, ∞)… (2)

From (1) and (2), we get

x ∈ (–∞, 5) ∩ (–5, ∞)

x ∈ (–5, 5)

∴ The solution of the given system of inequations is (–5, 5).

9. 3x – 1 ≥ 5, x + 2 > -1

Solution:

Given:

3x – 1 ≥ 5 and x + 2 > –1

Let us consider the first inequality.

3x – 1 ≥ 5

3x – 1 + 1 ≥ 5 + 1

3x ≥ 6

Divide both the sides by 3 we get,

3x/3 ≥ 6/3

x ≥ 2

∴ x ∈ [2, ∞)… (1)

Now, let us consider the second inequality.

x + 2 > –1

x + 2 – 2 > –1 – 2

x > –3

∴ x ∈ (–3, ∞)… (2)

From (1) and (2), we get

x ∈ [2, ∞) ∩ (–3, ∞)

x ∈ [2, ∞)

∴ The solution of the given system of inequations is [2, ∞).

10. 11 – 5x > –4, 4x + 13 ≤ –11

Solution:

Given:

11 – 5x > –4 and 4x + 13 ≤ –11

Let us consider the first inequality.

11 – 5x > –4

11 – 5x – 11 > –4 – 11

–5x > –15

Divide both the sides by 5 we get,

-5x/5 > -15/5

–x > –3

x < 3

∴ x ∈ (–∞, 3) (1)

Now, let us consider the second inequality.

4x + 13 ≤ –11

4x + 13 – 13 ≤ –11 – 13

4x ≤ –24

Divide both the sides by 4 we get,

4x/4 ≤ –24/4

x ≤ –6

∴ x ∈ (–∞, –6] (2)

From (1) and (2), we get

x ∈ (–∞, 3) ∩ (–∞, –6]

x ∈ (–∞, –6]

∴ The solution of the given system of inequations is (–∞, –6].

EXERCISE 15.3 PAGE NO: 15.22

Solve each of the following system of equations in R.

1. |x + 1/3| > 8/3

Solution:

Let ‘r’ be a positive real number and ‘a’ be a fixed real number. Then,

|x + a| > r ⟺ x > r – a or x < – (a + r)

Here, a = 1/3 and r = 8/3

x > 8/3 – 1/3 or x < – (8/3 + 1/3)

x > (8-1)/3 or x < – (8+1)/3

x > 7/3 or x < – 9/3

x > 7/3 or x < – 3

x ∈ (7/3, ∞) or x ∈ (–∞, -3)

∴ x ∈ (–∞, -3) ∪ (7/3, ∞)

2. |4 – x| + 1 < 3

Solution:

|4 – x | + 1 < 3

Let us subtract 1 from both the sides, we get

|4 – x| + 1 – 1 < 3 – 1

|4 – x| < 2

Let ‘r’ be a positive real number and ‘a’ be a fixed real number. Then,

|a – x| < r ⟺ a – r < x < a + r

Here, a=4 and r=2

4 – 2 < x < 4 + 2

2 < x < 6

∴ x ∈ (2, 6)

3. | (3x – 4)/2 | ≤ 5/12

Solution:

Given:

| (3x – 4)/2 | ≤ 5/12

We can rewrite it as

| 3x/2 – 4/2 | ≤ 5/12

| 3x/2 – 2 | ≤ 5/12

Let ‘r’ be a positive real number and ‘a’ be a fixed real number. Then,

|x – a| ≤ r ⟺ a – r ≤ x ≤ a + r

Here, a = 2 and r = 5/12

2 – 5/12 ≤ 3x/2 ≤ 2 + 5/12

(24-5)/12 ≤ 3x/2 ≤ (24+5)/12

19/12 ≤ 3x/2 ≤ 29/12

Now, multiplying the whole inequality by 2 and dividing by 3, we get

19/18 ≤ x ≤ 29/18

∴ x ∈ [19/18, 29/18]

4. |x – 2| / (x – 2) > 0

Solution:

Given:

|x – 2| / (x – 2) > 0

Clearly it states, x≠2 so two case arise:

Case1: x–2>0

x>2

In this case |x–2| = x – 2

x ϵ (2, ∞)….(1)

Case 2: x–2<0

x<2

In this case, |x–2|= – (x–2)

– (x – 2) / (x – 2) > 0

– 1 > 0

Inequality doesn’t get satisfy

This case gets nullified.

∴ x ∈ (2, ∞) from (1)

5. 1 / (|x| – 3) < ½

Solution:

We know that, if we take reciprocal of any inequality we need to change the inequality as well.

Also, |x| – 3 ≠ 0

|x| > 3 or |x| < 3

For |x| < 3

–3 < x < 3

x ∈ (–3, 3) …. (1)

The equation can be re–written as

|x| – 3 > 2

Let us add 3 on both the sides, we get

|x| – 3 + 3 > 2 + 3

|x| > 5

Let ‘a’ be a fixed real number. Then,

|x | > a ⟺ x < –a or x > a

Here, a = 5

x < –5 or x > 5 …. (2)

From (1) and (2)

x ∈ (–∞,–5 ) or x ∈ (5, ∞)

∴ x ∈ (–∞,–5 ) ⋃ (–3, 3) ⋃ (5, ∞)

6. (|x + 2| – x) / x < 2

Solution:

Given:

(|x + 2| – x) / x < 2

Let us rewrite the equation as

|x + 2|/x – x/x < 2

|x + 2|/x – 1 < 2

By adding 1 on both sides, we get

|x + 2|/x – 1 + 1 < 2 + 1

|x + 2|/x < 3

By subtracting 3 on both sides, we get

|x + 2|/x – 3 < 3 – 3

|x + 2|/x – 3 < 0

Clearly it states, x ≠ -2 so two case arise:

Case1: x + 2 > 0

x > –2

In this case |x+2| = x + 2

x + 2/x – 3 < 0

(x + 2 – 3x)/x < 0

– (2x – 2)/x < 0

(2x – 2)/x < 0

Let us consider only the numerators, we get

2x – 2 > 0

x>1

x ϵ (1, ∞) ….(1)

Case 2: x + 2 < 0

x < –2

In this case, |x+2| = – (x + 2)

-(x+2)/x – 3 < 0

(-x – 2 – 3x)/x < 0

– (4x + 2)/x < 0

(4x + 2)/x < 0

Let us consider only the numerators, we get

4x + 2 > 0

x > – ½

But x < -2

From the denominator we have,

x ∈ (–∞ , 0) …(2)

From (1) and (2)

∴ x ∈ (–∞ , 0) ⋃ (1, ∞)

EXERCISE 15.4 PAGE NO: 15.24

1. Find all pairs of consecutive odd positive integers, both of which are smaller than 10, such that their sum is more than 11.

Solution:

Let ‘x’ be the smaller of the two consecutive odd positive integers. Then the other odd integer is x + 2.

Given:

Both the integers are smaller than 10 and their sum is more than 11.

So,

x + 2 < 10 and x + (x + 2) > 11

x < 10 – 2 and 2x + 2 > 11

x < 8 and 2x > 11 – 2

x < 8 and 2x > 9

x < 8 and x > 9/2

9/2 < x < 8

Note the odd positive integers lying between 4.5 and 8.

x = 5, 7 [Since, x is an odd integer]

x < 10 [From the given statement]

9/2 < x < 10

Note that, the upper limit here has shifted from 8 to 10. Now, x is odd integer from 4.5 to 10.

So, the odd integers from 4.5 to 10 are 5, 7 and 9.

Now, let us find pairs of consecutive odd integers.

Let x = 5, then (x + 2) = (5 + 2) = 7.

Let x = 7, then (x + 2) = (7 + 2) = 9.

Let x = 9, then (x + 2) = (9 + 2) = 11. But, 11 is greater than 10.

∴ The required pairs of odd integers are (5, 7) and (7, 9)

2. Find all pairs of consecutive odd natural number, both of which are larger than 10, such that their sum is less than 40.

Solution:

Let ‘x’ be the smaller of the two consecutive odd natural numbers. Then the other odd number is x + 2.

Given:

Both the natural numbers are greater than 10 and their sum is less than 40.

So,

x > 10 and x + x + 2 <40

x > 10 and 2x < 38

x > 10 and x < 38/2

x > 10 and x < 19

10 < x < 19

From this inequality, we can say that x lies between 10 and 19.

So, the odd natural numbers lying between 10 and 19 are 11, 13, 15 and 17. (Excluding 19 as x < 19)

Now, let us find pairs of consecutive odd natural numbers.

Let x = 11, then (x + 2) = (11 + 2) = 13

Let x = 13, then (x + 2) = (13 + 2) = 15

Let x = 15, then (x + 2) = (15 + 2) = 17

Let x = 17, then (x + 2) = (17 + 2) = 19.

x = 11, 13, 15, 17 [Since, x is an odd number]

∴ The required pairs of odd natural numbers are (11, 13), (13, 15), (15, 17) and (17, 19)

3. Find all pairs of consecutive even positive integers, both of which are larger than 5, such that their sum is less than 23.

Solution:

Let ‘x’ be the smaller of the two consecutive even positive integers. Then the other even integer is x + 2.

Given:

Both the even integers are greater than 5 and their sum is less than 23.

So,

x > 5 and x + x + 2 < 23

x > 5 and 2x < 21

x > 5 and x < 21/2

5 < x < 21/2

5 < x < 10.5

From this inequality, we can say that x lies between 5 and 10.5.

So, the even positive integers lying between 5 and 10.5 are 6, 8 and 10.

Now, let us find pairs of consecutive even positive integers.

Let x = 6, then (x + 2) = (6 + 2) = 8

Let x = 8, then (x + 2) = (8 + 2) = 10

Let x = 10, then (x + 2) = (10 + 2) = 12.

x = 6, 8, 10 [Since, x is even integer]

∴ The required pairs of even positive integer are (6, 8), (8, 10) and (10, 12)

4. The marks scored by Rohit in two tests were 65 and 70. Find the minimum marks he should score in the third test to have an average of at least 65 marks.

Solution:

Given:

Marks scored by Rohit in two tests are 65 and 70.

Let marks in the third test be x.

So let us find minimum x for which the average of all three papers would be at least 65 marks.

That is,

Average marks in three papers ≥ 65 …(i)

Average is given by:

Average = (sum of all numbers)/(Total number of items)

= (marks in 1st two papers + marks in third test)/3

= (65 + 70 + x)/3

= (135 + x)/3

Substituting this value of average in the inequality (i), we get

(135 + x)/3 ≥ 65

(135 + x) ≥ 65 × 3

(135 + x) ≥ 195

x ≥ 195 – 135

x ≥ 60

This inequality means that Rohit should score at least 60 marks in his third test to have an average of at least 65 marks.

So, the minimum marks to get an average of 65 marks is 60.

∴ The minimum marks required in the third test is 60.

5. A solution is to be kept between 86o and 95oF. What is the range of temperature in degree Celsius, if the Celsius (C)/Fahrenheit (F) conversion formula is given by F = 9/5C + 32.

Solution:

Let us consider F1 = 86o F

And F2 = 95o

We know, F = 9/5C + 32

F1 = 9/5 C1 + 32

F1 – 32 = 9/5 C1

C1 = 5/9 (F1 – 32)

= 5/9 (86 – 32)

= 5/9 (54)

= 5 × 6

= 30o C

Now,

F2 = 9/5 C2 + 32

F2 – 32 = 9/5 C2

C2 = 5/9 (F2 – 32)

= 5/9 (95 – 32)

= 5/9 (63)

= 5 × 7

= 35o C

∴ The range of temperature of the solution in degree Celsius is 30° C and 35° C.

6. A solution is to be kept between 30oC and 35oC. What is the range of temperature in degree Fahrenheit?

Solution:

Let us consider C1 = 30o C

And C2 = 35o

We know, F = 9/5C + 32

F1 = 9/5 C1 + 32

= 9/5 × 30 + 32

= 9 × 6 + 32

= 54 + 32

= 86o F

Now,

F2 = 9/5 C2 + 32

= 9/5 × 35 + 32

= 9 × 7 + 32

= 63 + 32

= 95o F

∴ The range of temperature of the solution in degree Fahrenheit is 86° F and 95° F.

EXERCISE 15.5 PAGE NO: 15.28

Represent to solution set of the following inequations graphically in two dimensional plane:

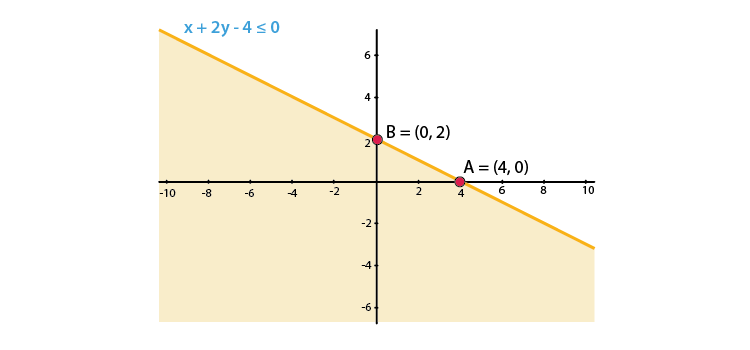
1. x + 2y – 4 ≤ 0

Solution:

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

x + 2y – 4 ≤ 0

So when,

x024
y210

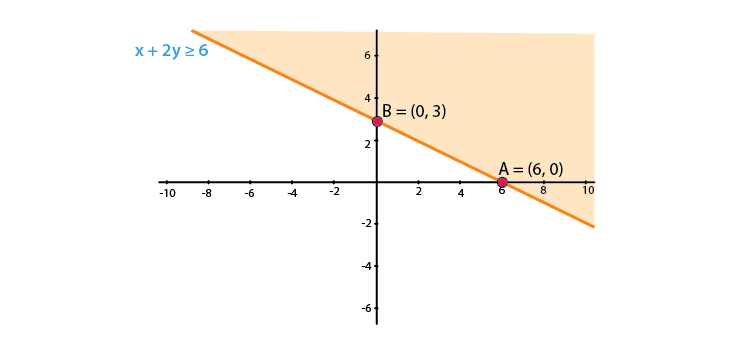
2. x + 2y ≥ 6

Solution:

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

x + 2y ≥ 6

So when,

x026
y320

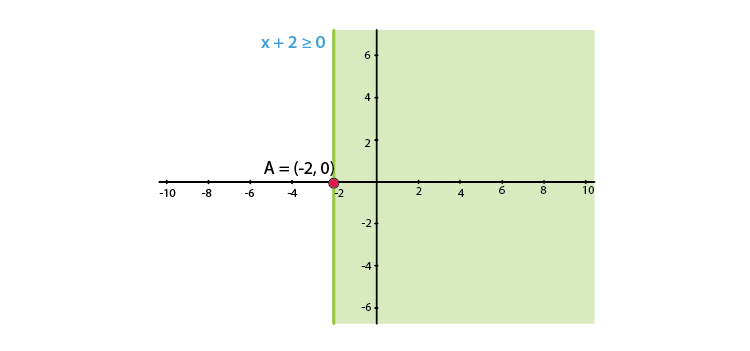
3. x + 2 ≥ 0

Solution:

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

x + 2 ≥ 0

x ≥ -2

As there is only one variable ‘x,’ and y = 0, which means that x has only one value when considered as an equation.

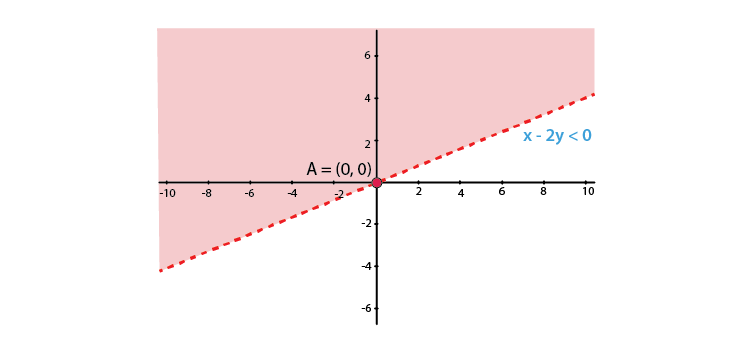
4. x – 2y < 0

Solution:

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

x – 2y < 0

x < 2y

So when,

x024
y012

5. – 3x + 2y ≤ 6

Solution:

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

– 3x + 2y ≤ 6

So when,

x02-2
y360

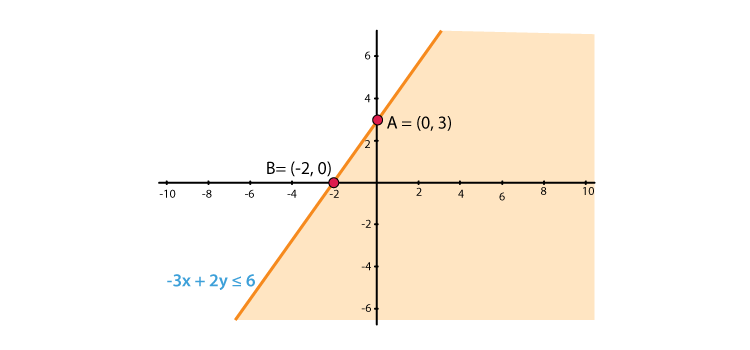
EXERCISE 15.6 PAGE NO: 15.30

1. Solve the following systems of linear inequations graphically.
(i) 2x + 3y ≤ 6, 3x + 2y ≤ 6, x ≥ 0, y ≥ 0

(ii) 2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0

(iii) x – y ≤ 1, x + 2y ≤ 8, 2x + y ≥ 2, x ≥ 0, y ≥ 0

(iv) x + y ≥ 1, 7x + 9y ≤ 63, x ≤ 6, y ≤ 5, x ≥ 0, y ≥ 0

(v) 2x + 3y ≤ 35, y ≥ 3, x ≥ 2, x ≥ 0, y ≥ 0

Solution:

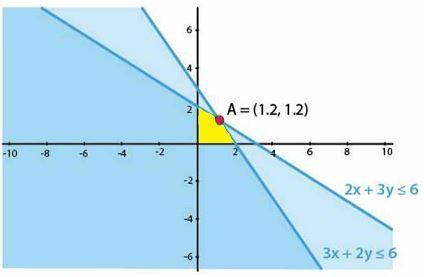
(i) 2x + 3y ≤ 6, 3x + 2y ≤ 6, x ≥ 0, y ≥ 0

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

2x + 3y ≤ 6

So when,

x013
y21.330

3x + 2y ≤ 6

So when,

x012
y31.50

x ≥ 0, y ≥ 0

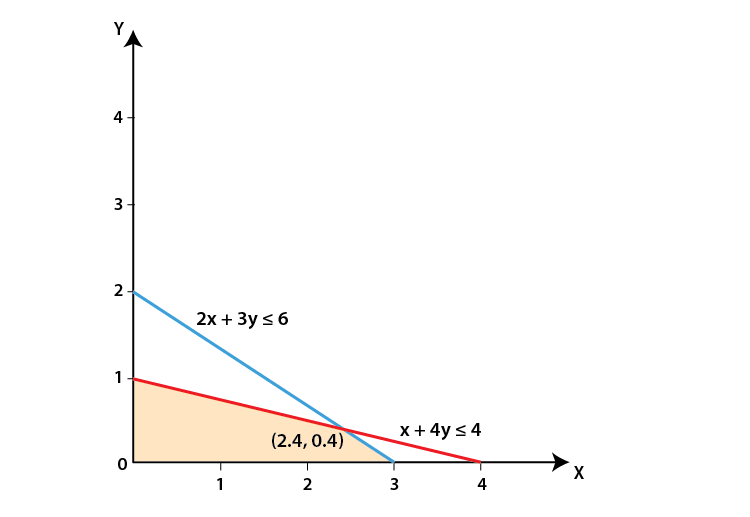
(ii) 2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

2x + 3y ≤ 6

So when,

x013
y21.330

x + 4y ≤ 4

So when,

x024
y10.50

x ≥ 0, y ≥ 0

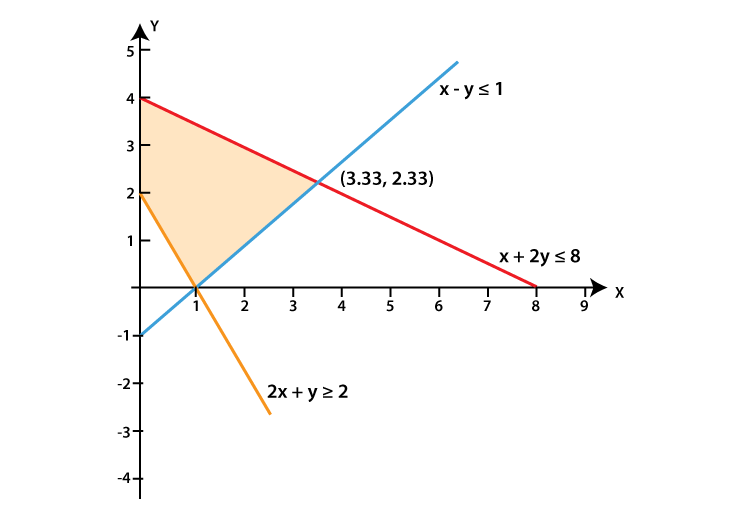
(iii) x – y ≤ 1, x + 2y ≤ 8, 2x + y ≥ 2, x ≥ 0, y ≥ 0

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

x – y ≤ 1

So when,

x021
y-110

x + 2y≤ 8

So when,

x048
y420

2x + y ≥ 2

So when,

x021
y2-20

x ≥ 0, y ≥ 0

(iv) x + y ≥ 1, 7x + 9y ≤ 63, x ≤ 6, y ≤ 5, x ≥ 0, y ≥ 0

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

x + y ≥ 1

So when,

x021
y1-10

7x + 9y ≤ 63

So when,

x059
y73.110

x ≤ 6, y ≤ 5 and x ≥ 0, y ≥ 0

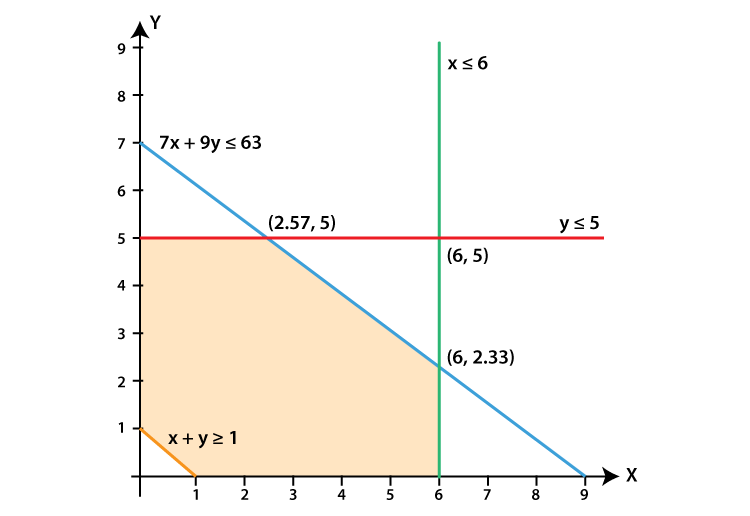
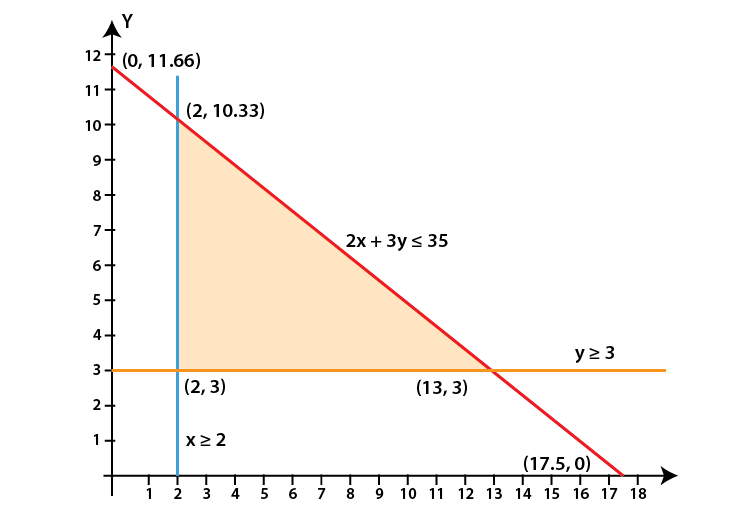
(v) 2x + 3y ≤ 35, y ≥ 3, x ≥ 2, x ≥ 0, y ≥ 0

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

2x + 3y ≤ 35

So when,

x0517.5
y11.6678.330

y ≥ 3, x ≥ 2, x ≥ 0, y ≥ 0

2. Show that the solution set of the following linear inequations is empty set:
(i) x – 2y ≥ 0, 2x – y ≤ –2, x ≥ 0, y ≥ 0

(ii) x + 2y ≤ 3, 3x + 4y ≥ 12, y ≥ 1, x ≥ 0, y ≥ 0

Solution:

(i) x – 2y ≥ 0, 2x – y ≤ –2, x ≥ 0, y ≥ 0

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

x – 2y ≥ 0

So when,

x024
y012

2x – y ≤ –2

So when,

x01-1
y240

x ≥ 0, y ≥ 0

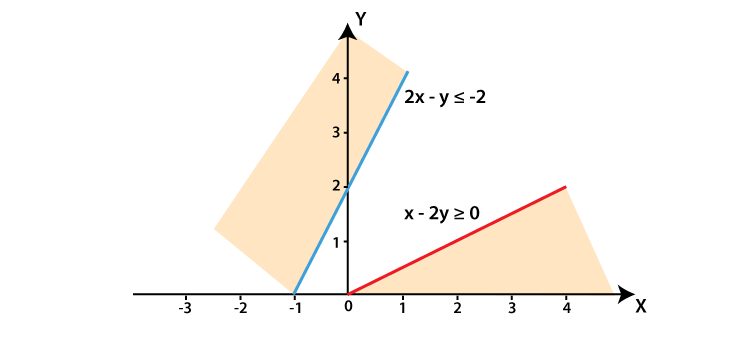
The lines do not intersect each other for x ≥ 0, y ≥ 0

Hence, there is no solution for the given inequations.

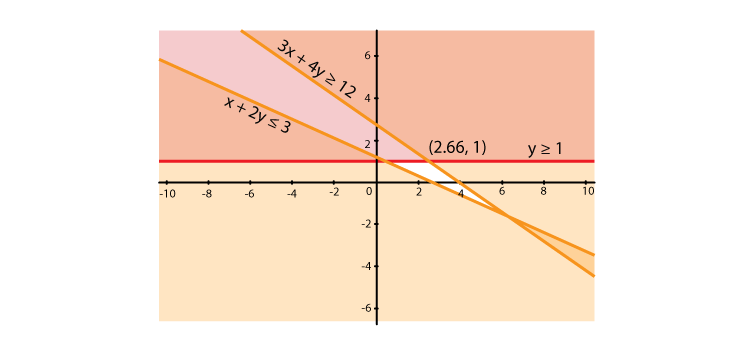
(ii) x + 2y ≤ 3, 3x + 4y ≥ 12, y ≥ 1, x ≥ 0, y ≥ 0

We shall plot the graph of the equation and shade the side containing solutions of the inequality,

You can choose any value but find the two mandatory values which are at x = 0 and y = 0, i.e., x and y–intercepts always,

x + 2y ≤ 3

So when,

x013
y1.510

3x + 4y ≥ 12

So when,

x024
y31.50

y ≥ 1, x ≥ 0, y ≥ 0

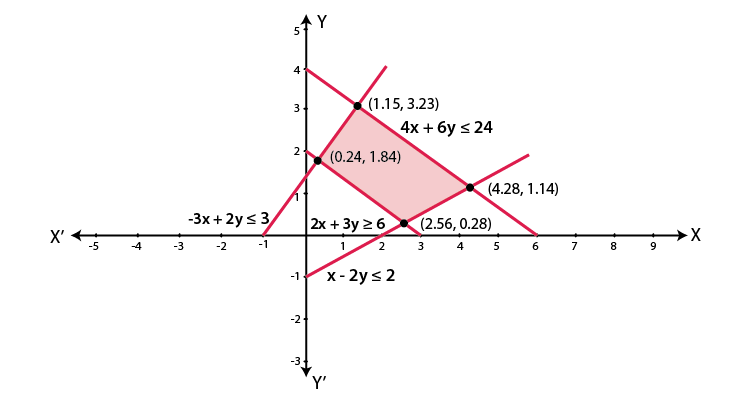
3. Find the linear inequations for which the shaded area in Fig. 15.41 is the solution set. Draw the diagram of the solution set of the linear inequations.

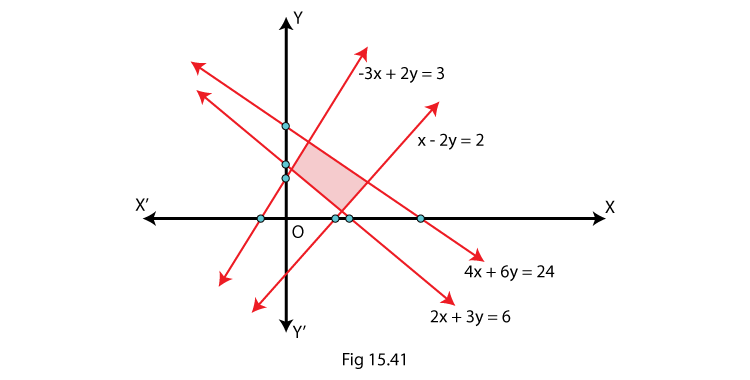
Solution:

Here, we shall apply the concept of a common solution area to find the signs of inequality by using their given equations and the given common solution area (shaded part).

We know that,

If a line is in the form ax + by = c and c is positive constant. (In case of negative c, the rule becomes opposite), so there are two cases which are,

If a line is above the origin:

(i) If the shaded area is below the line then ax + by < c

(ii) If the shaded area is above the line then ax + by > c

If a line is below the origin then the rule becomes opposite.

So, according to the rules

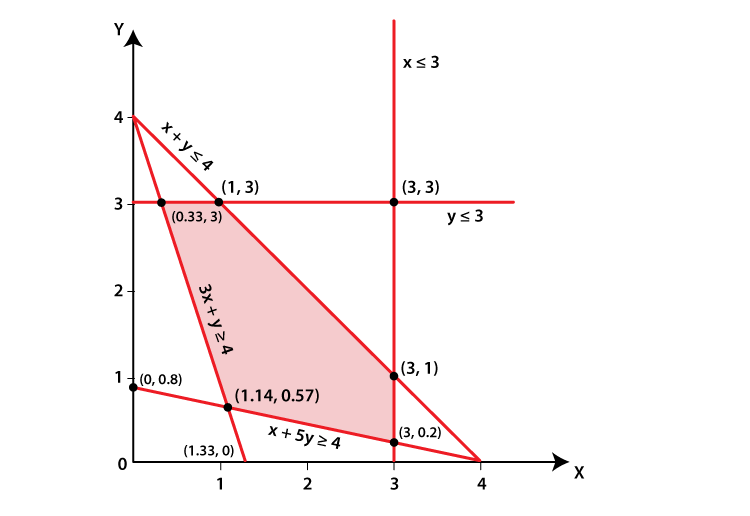
4. Find the linear inequations for which the solution set is the shaded region given in Fig. 15.42.

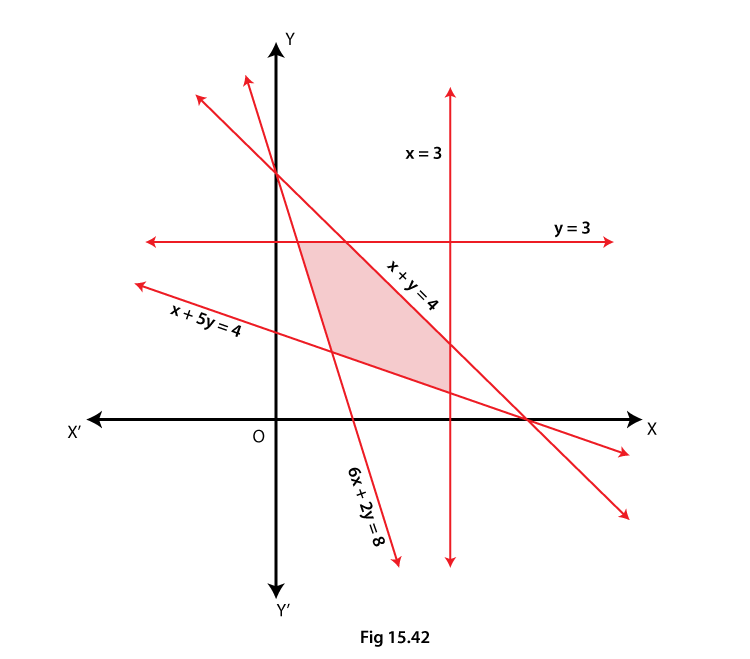
Solution:

Here, we shall apply the concept of a common solution area to find the signs of inequality by using their given equations and the given common solution area (shaded part).

We know that,

If a line is in the form ax + by = c and c is positive constant.

So, according to the rules

RD Sharma Solutions for Class 11 Maths Chapter 15: Download PDF

RD Sharma Solutions for Class 11 Maths Chapter 15–Linear Inequations

Download PDF: RD Sharma Solutions for Class 11 Maths Chapter 15–Linear Inequations PDF

Chapterwise RD Sharma Solutions for Class 11 Maths :

About RD Sharma

RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.

R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.

Read More