Maharashtra Board for Class 8, Maths Chapter 17

Class 8: Maths Chapter 17 solutions. Complete Class 8 Maths Chapter 17 Notes.

Contents

1 Maharashtra Board Solutions Class 8-Maths (Practice Set 17.1): Chapter 17- Factorisation of Algebraic Expressions
2 Download PDF
3 Chapterwise Maharashtra Board Solutions Class 8 Maths :
4 FAQs
5 About Maharashtra State Board (MSBSHSE)

Maharashtra Board Solutions Class 8-Maths (Practice Set 17.1): Chapter 17- Factorisation of Algebraic Expressions

Maharashtra Board 8th Maths Chapter 17, Class 8 Maths Chapter 17 solutions

Question 1.
In a circle with centre P, chord AB is drawn of length 13 cm, seg PQ ⊥ chord AB, then find l(QB)

Solution:
seg PQ ⊥ chord AB … [Given]
∴l(QB) = 12 l(AB)… [Perpendicular drawn from the centre of a circle to its chord bisects the chord]
∴l(QB) = 12 x 13 …[∵ l(AB) = 13 cm]
∴l(QB) = 6.5 cm

Question 2.
Radius of a circle with centre O is 25 cm. Find the distance of a chord from the centre if length of the chord is 48 cm.

Solution:
seg OP ⊥ chord CD … [Given]
∴l(PD) = 12 l(CD) … [Perpendicular drawn from the centre of a circle to its chord bisects the chord]
∴l(PD) = 12 x 48 …[∵ l(CD) = 48 cm]
∴l(PD) = 24 cm …(i)
In ∆OPD, m∠OPD = 90°
∴[l(OD)]² = [l(OP)]² + [l(PD)]² … [Pythagoras theorem]
∴(25)² = [l(OP)]² + (24)² … [From (i) and l(OD) = 25 cm]
∴(25)² – (24)² = [l(OP)]²
∴(25 + 24) (25 – 24) = [l(OP)]² …[∵ a² – b² = (a + b) (a – b)]
∴49 x 1 = [l(OP)]²
∴[l(OP)]² = 49
∴l(OP) = √49 …[Taking square root of both sides]
∴l(OP) = 7 cm
∴The distance of the chord from the centre of the circle is 7 cm.

Question 3.
O is centre of the circle. Find the length of radius, if the chord of length 24 cm is at a distance of 9 cm from the centre of the

Solution:
Let seg OP ⊥ chord AB
∴ l(AP) = 12 l(AB) … [Perpendicular drawn from the centre of a circle to its chord bisects the chord]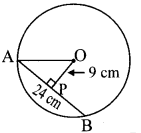

∴l(AP) = 12 x 24 …[∵ l(AB) = 24 cm]
∴l(AP) = 12 cm …(i)
In ∆OPA, m∠OPA = 90°
∴[l(AO)]² = [l(OP)]² + [l(AP)]² … [Pythagoras theorem]
∴[l(AO)]² = (9)² + (12)² … [From (i) and l(OP) = 9 cm]
= 81 + 144
∴[l(AO)]² = 225
∴l(AO) = √225 …[Taking square root of both sides]
∴l(AO) = 15 cm
∴The length of radius of the circle is 15 cm.

Question 4.
C is the centre of the circle whose radius is 10 cm. Find the distance of the chord from the centre if the length of the chord is 12 cm.
Solution:
Let seg AB be the chord of the circle with centre C.
Draw seg CD ⊥ chord AB.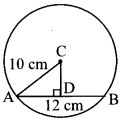

∴l(AD) = 12 l(AB) …[Perpendicular drawn from the centre of a circle to its chord bisects the chord]
= 12 x 12 …[∵ l(AB) = 12 cm]
∴l(AD) = 6 cm …(i)
∴In ∆ACD, m∠ADC = 90°
∴[l(AC)]² = [l(AD)]² + [l(CD)]² … [Pythagoras theorem]
∴(10)² = (6)² + [l(CD)]² … [From (i) and l(AC) = 10 cm]
∴(10)² – (6)² = [l(CD)]²
∴100 – 36 = [l(CD)]²
∴64 = [l(CD)]²
i. e. [l(CD)]² = 64
∴l(CD) = √64 …[Taking square root of both sides]
∴l(CD) = 8 cm
∴The distance of the chord from the centre of the circle is 8 cm.

Intext Questions and Activities

Question 1.
In the given figure, O is the centre of the circle. With reference to the figure fill in the blanks. (Textbook pg. No. 114)

Solution:

Seg OD is radius of the circle.
Seg AB is diameter of the circle.
Seg PQ is chord of the circle.
∠DOB is the central angle.
Minor arc : arc AXD, arc BD, arc AP, arc PQ, arc BQ, etc.
Major arc : arc PAB, arc PDQ, arc PDB, arc ADQ, etc.
Semicircular arc : arc ADB, arc AQB.
m (arc DB) = m∠DOB
m (arc DAB) = 360° – m∠DOB

Question 2.
Draw chord AB of a circle with centre O. Draw perpendicular OP to chord AB. Measure seg AP and seg PB. What do you observe. (Textbook pg. no. 114)
Solution:
l(AP) = l(PB) = 0.9 cm
∴the perpendicular drawn from the centre of the circle to its chord bisects the chord.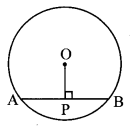

Question 3.
Draw five circles with different radii. Draw a chord and perpendicular from the centre to each chord in each circle. Verify with a divider that the two parts of the chords are equal. (Textbook pg. no. 114)
Solution:
[Students should attempt the above activities on their own.]

Question 4.
Draw five circles of different radii on a paper. Draw a chord in each circle. Find the midpoint of each chord. Join the centre of the circle and midpoint of the chord as shown in the figure. Name the chord as AB and midpoint of the chord as P. Check with set-square or protractor that ∠APO or ∠BPO are right angles.
Check whether the same result is observed for the chord of each circle. (Textbook pg, no. 115)
Solution:
[Students should attempt the above activities on their own.]

Download PDF

Maharashtra Board Solutions Class 8-Maths (Practice Set 17.1): Chapter 17- Factorisation of Algebraic Expressions

Download PDF: Maharashtra Board Solutions Class 8-Maths (Practice Set 17.1): Chapter 17- Factorisation of Algebraic Expressions PDF

Chapterwise Maharashtra Board Solutions Class 8 Maths :

FAQs

Where do I get the Maharashtra State Board Books PDF For free download?

You can download the Maharashtra State Board Books from the eBalbharti official website, i.e. cart.ebalbharati.in or from this article.

How to Download Maharashtra State Board Books?

Students can get the Maharashtra Books for primary, secondary, and senior secondary classes from here. You can view or download the Maharashtra State Board Books from this page or from the official website for free of cost. Students can follow the detailed steps below to visit the official website and download the e-books for all subjects or a specific subject in different mediums.
Step 1: Visit the official website ebalbharati.in
Step 2: On the top of the screen, select “Download PDF textbooks”
Step 3: From the “Classes” section, select your class.
Step 4: From “Medium”, select the medium suitable to you.
Step 5: All Maharashtra board books for your class will now be displayed on the right side.
Step 6: Click on the “Download” option to download the PDF book.

Who developed the Maharashtra State board books?

As of now, the MSCERT and Balbharti are responsible for the syllabus and textbooks of Classes 1 to 8, while Classes 9 and 10 are under the Maharashtra State Board of Secondary and Higher Secondary Education (MSBSHSE).

How many state boards are there in Maharashtra?

The Maharashtra State Board of Secondary & Higher Secondary Education, conducts the HSC and SSC Examinations in the state of Maharashtra through its nine Divisional Boards located at Pune, Mumbai, Aurangabad, Nasik, Kolhapur, Amravati, Latur, Nagpur and Ratnagiri.

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC.

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.