RD Sharma Solutions for Class 11 Maths Chapter 25–Parabola
RD Sharma Solutions for Class 11 Maths Chapter 25–Parabola

Class 11: Maths Chapter 25 solutions. Complete Class 11 Maths Chapter 25 Notes.

RD Sharma Solutions for Class 11 Maths Chapter 25–Parabola

RD Sharma 11th Maths Chapter 25, Class 11 Maths Chapter 25 solutions

1. Find the equation of the parabola whose:
(i) focus is (3, 0) and the directrix is 3x + 4y = 1

(ii) focus is (1, 1) and the directrix is x + y + 1 = 0

(iii) focus is (0, 0) and the directrix is 2x – y – 1 = 0

(iv) focus is (2, 3) and the directrix is x – 4y + 1 = 0

Solution:

(i) focus is (3, 0) and the directrix is 3x + 4y = 1

Given:

The focus S(3, 0) and directrix(M) 3x + 4y – 1 = 0.

Let us assume P(x, y) be any point on the parabola.

The distance between two points (x1, y1) and (x2, y2) is given as:

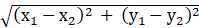
And the perpendicular distance from the point (x1, y1) to the line ax + by + c = 0 is

So by equating both, we get

Upon cross multiplication, we get

25x2 + 25y2 – 150x + 225 = 9x2 + 16y2 – 6x – 8y + 24xy + 1

16x2 + 9y2 – 24xy – 144x + 8y + 224 = 0

∴The equation of the parabola is 16x2 + 9y2 – 24xy – 144x + 8y + 224 = 0

(ii) focus is (1, 1) and the directrix is x + y + 1 = 0

Given:

The focus S(1, 1) and directrix(M) x + y + 1 = 0.

Let us assume P(x, y) be any point on the parabola.

The distance between two points (x1, y1) and (x2, y2) is given as:

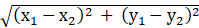
And the perpendicular distance from the point (x1, y1) to the line ax + by + c = 0 is

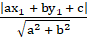
So by equating both, we get

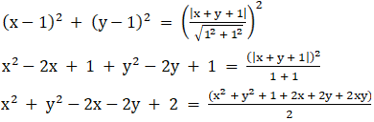
Upon cross multiplication, we get

2x2 + 2y2 – 4x – 4y + 4 = x2 + y2 + 2x + 2y + 2xy + 1

x2 + y2 + 2xy – 6x – 6y + 3 = 0

∴ The equation of the parabola is x2 + y2 + 2xy – 6x – 6y + 3 = 0

(iii) focus is (0, 0) and the directrix is 2x – y – 1 = 0

Given:

The focus S(0, 0) and directrix(M) 2x – y – 1 = 0.

Let us assume P(x, y) be any point on the parabola.

The distance between two points (x1, y1) and (x2, y2) is given as:

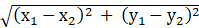
And the perpendicular distance from the point (x1, y1) to the line ax + by + c = 0 is

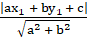
So by equating both, we get

Upon cross multiplication, we get

5x2 + 5y2 = 4x2 + y2 – 4x + 2y – 4xy + 1

x2 + 4y2 + 4xy + 4x – 2y – 1 = 0

∴ The equation of the parabola is x2 + 4y2 + 4xy + 4x – 2y – 1 = 0

(iv) focus is (2, 3) and the directrix is x – 4y + 1 = 0

Given:

The focus S(2, 3) and directrix(M) x – 4y + 3 = 0.

Let us assume P(x, y) be any point on the parabola.

The distance between two points (x1, y1) and (x2, y2) is given as:

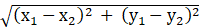
And the perpendicular distance from the point (x1, y1) to the line ax + by + c = 0 is

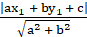
So by equating both, we get

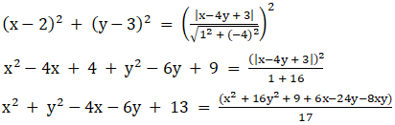
Upon cross multiplication, we get

17x2 + 17y2 – 68x – 102y + 221 = x2 + 16y2 + 6x – 24y – 8xy + 9

16x2 + y2 + 8xy – 74x – 78y + 212 = 0

∴ The equation of the parabola is 16x2 + y2 + 8xy – 74x – 78y + 212 = 0

2. Find the equation of the parabola whose focus is the point (2, 3) and directrix is the line x – 4y + 3 = 0. Also, find the length of its latus – rectum.

Solution:

Given:

The focus S(2, 3) and directrix(M) x – 4y + 3 = 0.

Let us assume P(x, y) be any point on the parabola.

The distance between two points (x1, y1) and (x2, y2) is given as:

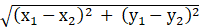
And the perpendicular distance from the point (x1, y1) to the line ax + by + c = 0 is

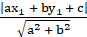
So by equating both, we get

Upon cross multiplication, we get

17x2 + 17y2 – 68x – 102y + 221 = x2 + 16y2 + 6x – 24y – 8xy + 9

16x2 + y2 + 8xy – 74x – 78y + 212 = 0

∴ The equation of the parabola is 16x2 + y2 + 8xy – 74x – 78y + 212 = 0.

Now, let us find the length of the latus rectum,

We know that the length of the latus rectum is twice the perpendicular distance from the focus to the directrix.

So by using the formula,

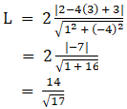
∴ The length of the latus rectum is 14/√17

3. Find the equation of the parabola, if
(i) the focus is at (-6, 6) and the vertex is at (-2, 2)

(ii) the focus is at (0, -3) and the vertex is at (0, 0)

(iii) the focus is at (0, -3) and the vertex is at (-1, -3)

(iv) the focus is at (a, 0) and the vertex is at (a′, 0)

(v) the focus is at (0, 0) and the vertex is at the intersection of the lines x + y = 1 and x – y = 3.

Solution:

(i) the focus is at (-6, 6) and the vertex is at (-2, 2)

Given:

Focus = (-6, 6)

Vertex = (-2, 2)

Let us find the slope of the axis (m1) = (6-2)/(-6-(-2))

= 4/-4

= -1

Let us assume m2 be the slope of the directrix.

m1m2 = -1

-1m2 = -1

m2 = 1

Now, let us find the point on directrix.

(-2, 2) = [(x-6/2), (y+6)/2]

By equating we get,

(x-6/2) = -2 and (y+6)/2 = 2

x-6 = -4 and y+6 = 4

x = -4+6 and y = 4-6

x = 2 and y = -2

So the point of directrix is (2, -2).

We know that the equation of the lines passing through (x1, y1) and having slope m is y – y1 = m(x – x1)

y – (-2) = 1(x – 2)

y + 2 = x – 2

x – y – 4 = 0

Let us assume P(x, y) be any point on the parabola.

The distance between two points (x1, y1) and (x2, y2) is given as:

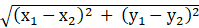
And the perpendicular distance from the point (x1, y1) to the line ax + by + c = 0 is

So by equating both, we get

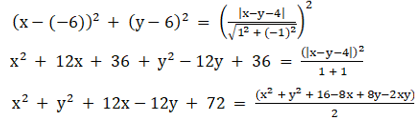
Now by cross multiplying, we get

2x2 + 2y2 + 24x – 24y + 144 = x2 + y2 – 8x + 8y – 2xy + 16

x2 + y2 + 2xy + 32x – 32y + 128 = 0

∴ The equation of the parabola is x2 + y2 + 2xy + 32x – 32y + 128 = 0

(ii) the focus is at (0, -3) and the vertex is at (0, 0)

Given:

Focus = (0, -3)

Vertex = (0, 0)

Let us find the slope of the axis (m1) = (-3-0)/(0-0)

= -3/0

= ∞

Since the axis is parallel to the x-axis, the slope of the directrix is equal to the slope of x-axis = 0

So, m2 = 0

Now, let us find the point on directrix.

(0, 0) = [(x-0/2), (y-3)/2]

By equating we get,

(x/2) = 0 and (y-3)/2 = 0

x = 0 and y – 3 = 0

x = 0 and y = 3

So the point on directrix is (0, 3).

We know that the equation of the lines passing through (x1, y1) and having slope m is y – y1 = m(x – x1)

y – 3 = 0(x – 0)

y – 3 = 0

Now, let us assume P(x, y) be any point on the parabola.

The distance between two points (x1, y1) and (x2, y2) is given as:

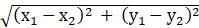
And the perpendicular distance from the point (x1, y1) to the line ax + by + c = 0 is

So by equating both, we get

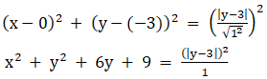
Now by cross multiplying, we get

x2 + y2 + 6y + 9 = y2 – 6y + 9

x2 + 12y = 0

∴ The equation of the parabola is x2 + 12y = 0

(iii) the focus is at (0, -3) and the vertex is at (-1, -3)

Given:

Focus = (0, -3)

Vertex = (-1, -3)

Let us find the slope of the axis (m1) = (-3-(-3))/(0-(-1))

= 0/1

= 0

We know, the products of the slopes of the perpendicular lines is – 1 for non – vertical lines.

Here the slope of the axis is equal to the slope of the x – axis. So, the slope of directrix is equal to the slope of y – axis i.e., ∞.

So, m2 = ∞

Now let us find the point on directrix.

(-1, -3) = [(x+0/2), (y-3)/2]

By equating we get,

(x/2) = -1 and (y-3)/2 = -3

x = -2 and y – 3 = -6

x = -2 and y = -6+3

x = -2 and y = -3

So, the point on directrix is (-2, -3)

We know that the equation of the lines passing through (x1, y1) and having slope m is y – y1 = m(x – x1)

y – (- 3) = ∞(x – (- 2))

(y+3)/ ∞ = x + 2

x + 2 = 0

Now, let us assume P(x, y) be any point on the parabola.

The distance between two points (x1, y1) and (x2, y2) is given as:

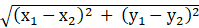
And the perpendicular distance from the point (x1, y1) to the line ax + by + c = 0 is

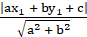
So by equating both, we get

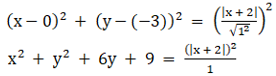
By cross multiplying, we get

x2 + y2 + 6y + 9 = x2 + 4x + 4

y2 – 4x + 6y + 5 = 0

∴ The equation of the parabola is y2 – 4x + 6y + 5 = 0

(iv) the focus is at (a, 0) and the vertex is at (a′, 0)

Given:

Focus = (a, 0)

Vertex = (a′, 0)

Let us find the slope of the axis (m1) = (0-0)/(a′, a)

= 0/(a′, a)

= 0

We know, the products of the slopes of the perpendicular lines is – 1 for non – vertical lines.

Here the slope of the axis is equal to the slope of the x – axis. So, the slope of directrix is equal to the slope of y – axis i.e., ∞.

So, m2 = ∞

Now let us find the point on directrix.

(a′, 0)= [(x+a/2), (y+0)/2]

By equating we get,

(x+a/2) = a′ and (y)/2 = 0

x + a = 2a′ and y = 0

x = (2a′ – a) and y = 0

So the point on directrix is (2a′ – a, 0).

We know that the equation of the lines passing through (x1, y1) and having slope m is y – y1 = m(x – x1)

y – (0) = ∞(x – (2a′ – a))

y/∞ = x + a – 2a′

x + a – 2a′ = 0

Now, let us assume P(x, y) be any point on the parabola.

The distance between two points (x1, y1) and (x2, y2) is given as:

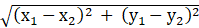
And the perpendicular distance from the point (x1, y1) to the line ax + by + c = 0 is

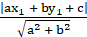
So by equating both, we get

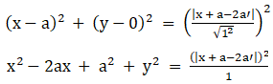
By cross multiplying we get,

x2 + y2 – 2ax + a2 = x2 + a2 + 4(a′)2 + 2ax – 4aa′ – 4a′x

y2 – (4a – 4a′)x + a2 – 4(a′)2 + 4aa′ = 0

∴ The equation of the parabola is y2 – (4a – 4a′)x + a2 – 4(a′)2 + 4aa′ = 0

(v) the focus is at (0, 0) and the vertex is at the intersection of the lines x + y = 1 and x – y = 3.

Given:

Focus = (0, 0)

Vertex = intersection of the lines x + y = 1 and x – y = 3.

So the intersecting point of above lines is (2, -1)

Vertex = (2, -1)

Slope of axis (m1) = (-1-0)/(2-0)

= -1/2

We know that the products of the slopes of the perpendicular lines is – 1.

Let us assume m2 be the slope of the directrix.

m1.m2 = -1

-1/2 . m2 = -1

So m2 = 2

Now let us find the point on directrix.

(2, -1) = [(x+0)/2, (y+0)/2]

(x)/2 = 2 and y/2 = -1

x = 4 and y = -2

The point on directrix is (4, – 2).

We know that the equation of the lines passing through (x1, y1) and having slope m is y – y1 = m(x – x1)

y – (- 2) = 2(x – 4)

y + 2 = 2x – 8

2x – y – 10 = 0

Now, let us assume P(x, y) be any point on the parabola.

The distance between two points (x1, y1) and (x2, y2) is given as:

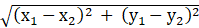
And the perpendicular distance from the point (x1, y1) to the line ax + by + c = 0 is

So by equating both, we get

By cross multiplying, we get

5x2 + 5y2 = 4x2 + y2 – 40x + 20y – 4xy + 100

x2 + 4y2 + 4xy + 40x – 20y – 100 = 0

∴ The equation of the parabola is x2 + 4y2 + 4xy + 40x – 20y – 100 = 0

4. Find the vertex, focus, axis, directrix and lotus – rectum of the following parabolas
(i) y2 = 8x

(ii) 4x2 + y = 0

(iii) y2 – 4y – 3x + 1 = 0

(iv) y2 – 4y + 4x = 0

(v) y2 + 4x + 4y – 3 = 0

Solution:

(i) y2 = 8x

Given:

Parabola = y2 = 8x

Now by comparing with the actual parabola y2 = 4ax

Then,

4a = 8

a = 8/4 = 2

So, the vertex is (0, 0)

The focus is (a, 0) = (2, 0)

The equation of the axis is y = 0.

The equation of the directrix is x = – a i.e., x = – 2

The length of the latus rectum is 4a = 8.

(ii) 4x2 + y = 0

Given:

Parabola => 4x2 + y = 0

Now by comparing with the actual parabola y2 = 4ax

Then,

4a = ¼

a = 1/(4 × 4)

= 1/16

So, the vertex is (0, 0)

The focus is = (0, -1/16)

The equation of the axis is x = 0.

The equation of the directrix is y = 1/16

The length of the latus rectum is 4a = ¼

(iii) y2 – 4y – 3x + 1 = 0

Given:

Parabola y2 – 4y – 3x + 1 = 0

y2 – 4y = 3x – 1

y2 – 4y + 4 = 3x + 3

(y – 2)2 = 3(x + 1)

Now by comparing with the actual parabola y2 = 4ax

Then,

4b = 3

b = ¾

So, the vertex is (-1, 2)

The focus is = (3/4 – 1, 2) = (-1/4, 2)

The equation of the axis is y – 2 = 0.

The equation of the directrix is (x – c) = -b

(x – (-1)) = -3/4

x = -1 – ¾

= -7/4

The length of the latus rectum is 4b = 3

(iv) y2 – 4y + 4x = 0

Given:

Parabola y2 – 4y + 4x = 0

y2 – 4y = – 4x

y2 – 4y + 4 = – 4x + 4

(y – 2)2 = – 4(x – 1)

Now by comparing with the actual parabola y2 = 4ax => (y – a)2 = – 4b(x – c)

Then,

4b = 4

b = 1

So, the vertex is (c, a) = (1, 2)

The focus is (b + c, a) = (1-1, 2) = (0, 2)

The equation of the axis is y – a = 0 i.e., y – 2 = 0

The equation of the directrix is x – c = b

x – 1 = 1

x = 1 + 1

= 2

Length of latus rectum is 4b = 4

(v) y2 + 4x + 4y – 3 = 0

Given:

The parabola y2 + 4x + 4y – 3 = 0

y2 + 4y = – 4x + 3

y2 + 4y + 4 = – 4x + 7

(y + 2)2 = – 4(x – 7/4)

Now by comparing with the actual parabola y2 = 4ax => (y – a)2 = – 4b(x – c)

Then,

4b = 4

b = 4/4 = 1

So, The vertex is (c, a) = (7/4, -2)

The focus is (- b + c, a) = (-1 + 7/4, -2) = (3/4, -2)

The equation of the axis is y – a = 0 i.e., y + 2 = 0

The equation of the directrix is x – c = b

x – 7/4 = 1

x = 1 + 7/4

= 11/4

Length of latus rectum is 4b = 4.

5. For the parabola, y2 = 4px find the extremities of a double ordinate of length 8p. Prove that the lines from the vertex to its extremities are at right angles.

Solution:

Given:

The parabola, y2 = 4px and a double ordinate of length 8p.

Let AB be the double ordinate of length 8p for the parabola y2 = 4px.

Now, let us compare to the actual parabola, y2 = 4ax

Then,

axis is y = 0

vertex is O(0, 0).

We know that double ordinate is perpendicular to the axis.

So, let us assume that the point at which the double ordinate meets the axis is (x1, 0).

Then the equation of the double ordinate is y = x1. It meets the parabola at the points (x1, 4p) and (x1, – 4p) as its length is 8p.

Now, let us find the value of x1 by substituting in the parabola.

(4p)2 = 4p(x1)

x1 = 4p.

The extremities of the double ordinate are A(4p, 4p) and B(4p, – 4p).

Assume the slopes of OA and OB be m1 and m2. Let us find their values.

m1 = (4p – 0)/(4p – 0)

= 4p/4p

= 1

m2 = (4p – 0)/(-4p – 0)

= 4p/-4p

= -1

So, m1.m2 = 1. – 1

= – 1

The product of slopes is -1. So, the lines OA and OB are perpendicular to each other.

Hence the extremities of double ordinate make right angle with the vertex.

6. Find the area of the triangle formed by the lines joining the vertex of the parabola x2 = 12y to the ends of its latus – rectum.

Solution:

Given:

The parabola, x2 = 12y

Now, let us compare to the actual parabola, y2 = 4ax

Then,

Vertex is O(0, 0)

Ends of latus rectum is (2b, b), (-2b, b)

4b = 12

b = 12/4

= 3

Ends of latus rectum = (2(3), 3), (- 2(3), 3)

Ends of latus rectum is A(6, 3), B(- 6, 3)

We know that area of the triangle with the vertices (x1, y1), (x2, y2) and (x3, y3) is

∴The area of the triangle is 18 sq.units.

7. Find the coordinates of the point of intersection of the axis and the directrix of the parabola whose focus is (3, 3) and directrix is 3x – 4y = 2. Find also the length of the latus – rectum.

Solution:

Given:

Focus = (3, 3)

Directrix = 3x – 4y = 2

Firstly let us find the slope of the directrix.

The slope of the line ax + by + c = 0 is –a/b

So, m1 = -3/-4

= ¾

Let us assume the slope of axis is m2.

m1.m2 = -1

¾ . m2 = -1

m2 = -4/3

We know that the equation of the line passing through the point (x1, y1) and having slope m is (y – y1) = m(x – x1)

y – 3 = -4/3 (x – 3)

3(y – 3) = – 4(x – 3)

3y – 9 = – 4x + 12

4x + 3y = 21

On solving the lines, the intersection point is (18/5, 11/5)

By using the formula to find the length is given as

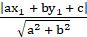
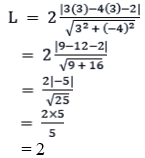
∴The length of the latus rectum is 2.

8. At what point of the parabola x2 = 9y is the abscissa three times that of ordinate?

Solution:

Given:

The parabola, x2 = 9y

Let us assume the point be (3y1, y1).

Now by substituting the point in the parabola we get,

(3y1)2 = 9(y1)

9y12 = 9y1

y12 – y1 = 0

y1(y1 – 1) = 0

y1 = 0 or y1 – 1 = 0

y1 = 0 or y1 = 1

The points is B (3(1), 1) => (3, 1)

∴The point is (3, 1).

RD Sharma Solutions for Class 11 Maths Chapter 25: Download PDF

RD Sharma Solutions for Class 11 Maths Chapter 25–Parabola

Download PDF:RD Sharma Solutions for Class 11 Maths Chapter 25–Parabola PDF

Chapterwise RD Sharma Solutions for Class 11 Maths :

About RD Sharma

RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.

R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.

Read More