ML Aggarwal Solutions for Class 7, maths Chapter 11

Class 7: Maths Chapter 11 solutions. Complete Class 7 Maths Chapter 11 Notes.

Contents

1 ML Aggarwal Solutions for Class 7 Maths Chapter 11- Triangles and its Properties
2 Download PDF
3 Chapterwise ML Aggarwal Solutions for Class 7 Maths :
4 About ML Aggarwal

ML Aggarwal Solutions for Class 7 Maths Chapter 11- Triangles and its Properties

ML Aggarwal 7th Maths Chapter 11, Class 7 Maths Chapter 11 solutions

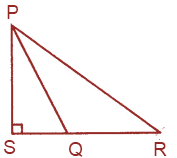
1. In the adjoining figure:
(i) Name the vertex opposite to side PQ.
(ii) Name the side opposite to vertex Q.
(iii) Name the angle opposite to side QR.
(iv) Name the side opposite to ∠R

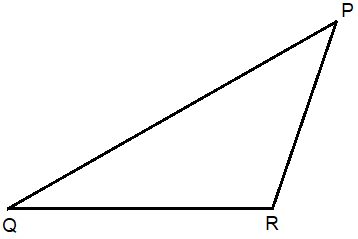
Solution:-

From the figure,

(i) R is the vertex opposite to side PQ.

(ii) PR is the side opposite to vertex Q.

(iii) P is the angle opposite to side QR.

(iv) PQ is the side opposite to ∠R.

2. Look at the figures given below and classify each of the triangles according to its

(a) Sides

(b) Angles

Solution:-

From the given figure,

(a) According to sides,

(i) Isosceles triangle, because two sides of triangle are equal.

(ii) Scalene triangle, because three sides are unequal.

(iii) Equilateral triangle, because three sides are equal.

(iv) Isosceles triangle, because two sides of triangle are equal.

(v) Scalene triangle, because three sides are unequal.

(vi) Isosceles triangle, because two sides of triangle are equal.

(b) According to angles,

(i) Acute angle triangle, because angle of triangle less than 90^o.

(ii) Right angled triangle, because one of the angle is equal to 90^o.

(iii) Acute angle triangle, because angle of triangle less than 90^o.

(iv) Obtuse angle triangle, because one of the angle is more than 90^o but less than 180^o.

(v) Obtuse angle triangle, because one of the angle is more than 90^o but less than 180^o.

(vi) Right angled triangle, because one of the angle is equal to 90^o.

3. In the given ∆PQR, if D is the mid-point of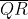
, then

(i)

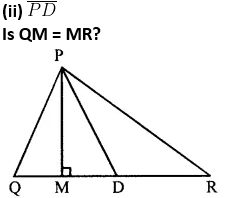
Solution:-

From the figure,

∆PQR, D is the mid-point of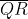

So,

(i)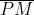
is Altitude

(ii)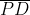
is Median

No, QM ≠ MR

4. Will an altitude always lie in the interior of triangle? If no, draw a rough sketch to show such a case.

Solution:-

No, it is not necessary an altitude may lie outside of triangle also.

A rough sketch to show such a case,

PS is the altitude of ∆PQR

Draw from P to the side QR

5. Can you think of a triangle in which two altitudes of the triangle are its sides? If yes, draw a rough sketch to show such a case.

Solution:-

Yes, it is a right angled triangle.

6. Draw rough sketches for the following:
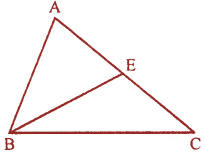
(i) In ΔABC, BE is a median of the triangle.

Solution:-

As per the condition given in the question,

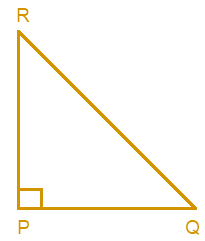
(ii) In ΔPQR, PQ and PR are altitudes of the triangle.

Solution:-

As per the condition given in the question,

(iii) In ΔXYZ, XL is an altitude in the exterior of the triangle.

Solution:-

As per the condition given in the question,

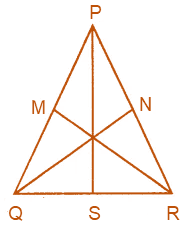
7. Take an equilateral triangle and draw its medians and altitudes and check that the medians and altitude are same.

Solution:-

Consider the equilateral triangle ΔPQR,

PS, QN and MR are altitudes of the triangle.

The altitudes of an equilateral triangle divide the sides into equal parts.

Hence, altitudes are also the medians of the triangle.

ML Aggarwal Solutions for Class 7 Maths Chapter 11 Image 14

Download PDF

ML Aggarwal Solutions for Class 7 Maths Chapter 11- Triangles and its Properties

Download PDF: ML Aggarwal Solutions for Class 7 Maths Chapter 11- Triangles and its Properties PDF

Chapterwise ML Aggarwal Solutions for Class 7 Maths :

About ML Aggarwal

M. L. Aggarwal, is an Indian mechanical engineer, educator. His achievements include research in solutions of industrial problems related to fatigue design. Recipient Best Paper award, Manipal Institute of Technology, 2004. Member of TSTE.