Maharashtra Board Solutions for Class 10-Maths (Part 1): Chapter 2- Quadratic Equations

Class 10: Maths Chapter 2 solutions. Complete Class 10 Maths Chapter 2 Notes.

Maharashtra Board Solutions for Class 10-Maths (Part 1): Chapter 2- Quadratic Equations

Maharashtra Board 10th Maths Chapter 2, Class 10 Maths Chapter 2 solutions

Practice Set 2.1

Question 1.
Write any two quadratic equations.
Solution:
i. y² – 7y + 12 = 0
ii. x² – 8 = 0

Question 2.
Decide which of the following are quadratic
i. x² – 7y + 2 = 0
ii. y² = 5y – 10
iii. y² + 1y = 2
iv. x + 1x = -2
v. (m + 2) (m – 5) = 03
vi. m³ + 3m² – 2 = 3m³
Solution:
i. The given equation is x² + 5x – 2 = 0
Here, x is the only variable and maximum index of the variable is 2.
a = 1, b = 5, c = -2 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

ii. The given equation is
y² = 5y – 10
∴ y² – 5y + 10 = 0
Here, y is the only variable and maximum index of the variable is 2.
a = 1, b = -5, c = 10 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

iii. The given equation is
y² + 1y = 2
∴ y³ + 1 = 2y …[Multiplying both sides by y]
∴ y³ – 2y + 1 = 0
Here, y is the only variable and maximum index of the variable is not 2.
∴ The given equation is not a quadratic equation.

iv. The given equation is
x + 1x = -2
∴ x² + 1 = -2x …[Multiplying both sides by x]
∴ x² + 2x+ 1 = 0
Here, x is the only variable and maximum index of the variable is 2.
a = 1, b = 2, c = 1 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

v. The given equation is
(m + 2) (m – 5) = 0
∴ m(m – 5) + 2(m – 5) = 0
∴ m² – 5m + 2m – 10 = 0
∴ m² – 3m – 10 = 0
Here, m is the only variable and maximum index of the variable is 2.
a = 1, b = -3, c = -10 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

vi. The given equation is
m³ + 3m² – 2 = 3m³
∴ 3m³ – m³ – 3m² + 2 = 0
∴ 2m³ – 3m² + 2 = 0
Here, m is the only variable and maximum
index of the variable is not 2.
∴ The given equation is not a quadratic equation.

Question 3.
Write the following equations in the form ax² + bx + c = 0, then write the values of a, b, c for each equation.
i. 2y = 10 – y²
ii. (x – 1)² = 2x + 3
iii. x² + 5x = – (3 – x)
iv. 3m² = 2m² – 9
v. P (3 + 6p) = – 5
vi. x² – 9 = 13
Solution:
i. 2y – 10 – y²
∴ y² + 2y – 10 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 1, b = 2, c = -10

ii. (x – 1)² = 2x + 3
∴ x² – 2x + 12x + 3
x² – 2x + 1 – 2x – 30
∴ x² – 4x – 2 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = -4, c = -2

iii. x² + 5x = – (3 – x)
∴ x² + 5x = -3 + x
∴ x² + 5x – x + 3 = 0
∴ x² + 4x + 3 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = 4, c = 3

iv. 3m² = 2m² – 9
∴ 3m² – 2m² + 9 = 0
∴ m² + 9 = 0
∴ m² + 0m + 9 = 0
Comparing the above equation with
am² + bm + c = 0, we get
a = 1, b = 0, c = 9

v. p (3 + 6p) = – 5
∴ 3p + 6p² = -5
∴ 6p² + 3p + 5 = 0
Comparing the above equation with
ap² + bp + c = 0, we get
a = 6, b = 3, c = 5

vi. x² – 9 = 13
∴ x² – 9 – 13 = 0
∴ x² – 22 = 0
∴ x² + 0x – 22 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = 0, c = -22

Question 4.
Determine whether the values given against each of the quadratic equation are the roots of the equation.
i. x² + 4x – 5 = 0; x = 1,-1
ii. 2m² – 5m = 0; m = 2, 52
Solution:
i. The given equation is
x² + 4x – 5 = 0 …(i)
Putting x = 1 in L.H.S. of equation (i), we get
L.H.S. = (1)² + 4(1) – 5 = 1 + 4 – 5 = 0
∴ L.H.S. = R.H.S.
∴ x = 1 is the root of the given quadratic equation.
Putting x = -1 in L.H.S. of equation (i), we get
L.H.S. = (-1)² + 4(-1) – 5 = 1 – 4 – 5 = -8
∴ LH.S. ≠ R.H.S.
∴ x = -1 ¡s not the root of the given quadratic equation.

ii. The given equation is
2m² – 5m = 0 …(i)
Putting m = 2 in L.H.S. of equation (i), we get
L.H.S. = 2(2)² – 5(2) = 2(4) -10 = 8 – 10 = -2
∴ L.H.S. ≠ R.H.S.
∴ m = 2 is not the root of the given quadratic equation.
Putting m = 52 in L.H.S. of equation (i), we get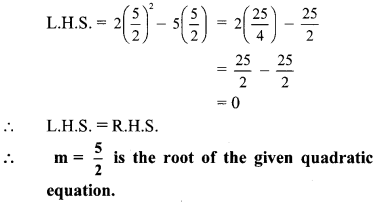

Question 5.
Find k if x = 3 is a root of equation kx² – 10x + 3 = 0.
Solution:
x = 3 is the root of the equation kx² – 10x + 3 = 0.
Putting x = 3 in the given equation, we get
k(3)² – 10(3) + 3 = 0
∴ 9k – 30 +3 = 0
∴ 9k – 27 = 0
∴ 9k = 27
∴ k = 279
∴ k = 3

Question 6.
One of the roots of equation 5m² + 2m + k = 0 is −75 Complete the following activity to find the value of ‘k’.
Solution:

Question 1.
x² + 3x – 5, 3x² – 5x, 5x²; Write the polynomials In the index form. Observe the coefficients and fill in the boxes. (Textbook p. no. 31)
Answer:
Index form of the given polynomials:
x² + 3x – 5, 3x² – 5x + 0, 5x² + 0x + 0
i. Coefficients of x2 are [1], [3] and [5] respectively, and these coefficients are non zero.
ii. Coefficients of x are 3, [-5] and [0] respectively.
iii. Constant terms are [-5], [0] and [0] respectively.
Here, constant terms of second and third polynomial is zero.

Question 2.
Complete the following table (Textbook p. no. 31)

Answer:

Question 3.
Decide which of the following are quadratic equations? (Textbook pg. no. 31)
i. 9y² + 5 = 0
ii. m³ – 5m² + 4 = 0
iii. (l + 2)(l – 5) = 0
Solution:
i. In the equation 9y² + 5 = 0, [y] is the only variable and maximum index of the variable is [2].
∴ It [is] a quadratic equation.

ii. In the equation m³ – 5m² + 4 = 0, [m] is the only variable and maximum index of the variable is not 2.
∴ It [is not] a quadratic equation.

iii. (l + 2)(l – 5) = 0
∴ l(l – 5) + 2(l – 5) = 0
∴ l² – 5l + 2l – 10 = 0
∴ l² – 3l – 10 = 0.
In this equation [l] is the only variable and maximum index of the variable is [2]
∴ it [is] a quadratic equation.

Question 4.
If x = 5 is a root of equation kx² – 14x – 5 = 0, then find the value of k by completing the following activity. (Textbook pg, no. 33)
Solution:

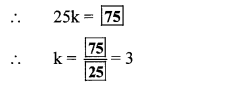
Practice Set 2.2

Question 1.
Solve the following quadratic equations by factorisation.
i. x² – 15x + 54 = 0
ii. x² + x – 20 = 0
iii. 2y² + 27y + 13 = 0
iv. 5m² = 22m + 15
v. 2x² – 2x + 12 = 0
vi. 6x – 2x = 1
vii. √2x² + 7x + 5√2 = 0 to solve this quadratic equation by factorisation complete the following activity
viii. 3x² – 2√6x + 2 = 0
ix. 2m(m – 24) = 50
x. 252 = 9
xi. 7m² = 21 m
xii. m² – 11 = 0
Solution: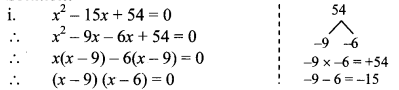

By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 9 = 0 or x – 6 = 0
∴ x = 9 or x = 6
∴ The roots of the given quadratic equation are 9 and 6.

By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 5 = 0 or x – 4 = 0
∴ x = -5 or x = 4
∴ The roots of the given quadratic equation are -5 and 4.

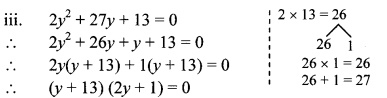
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ y + 13 = 0 or 2y + 1 = 0
∴ y = – 13 or 2y = -1
∴ y = -13 or y = –12
∴ The roots of the given quadratic equation are -13 and – 12

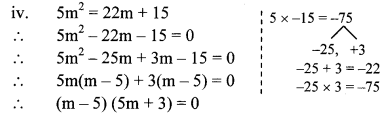
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ m – 5 = 0 or 5m + 3 = 0
∴ m = 5 or 5m = -3
∴ m = 5 or m = −35
∴ The roots of the given quadratic equation are 5 and – 35

By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ 3x – 2 = 0 or 2x + 1 = 0
∴ 3x = 2 or 2x = -1
∴ x = 23 or 2x = -1
∴ The roots of the given quadratic equation are 23 and −12.

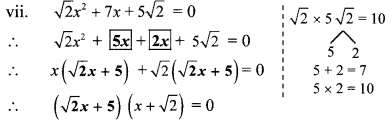
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get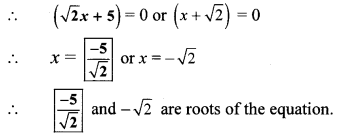

By using the property, if the product of two numbers is zero, then at least one of them is zero, we get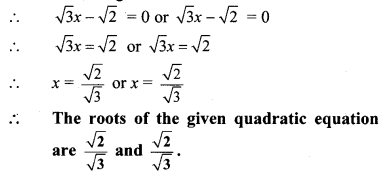

ix. 2m (m – 24) = 50
∴ 2m² – 48m = 50
∴ 2m² – 48m – 50 = 0
∴m² – 24m – 25 = 0 …[Dividing both sides by 2]

∴ m – 25 = 0 or m + 1 = 0
∴ m = 25 or m = -1
∴ The roots of thes given quadratic equation are 25 and -1.

x. 25m² = 9
∴ 25m² – 9 = 0
∴ (5m)² – (3)² = 0
∴ (5m + 3) (5m – 3) = 0
…. [∵a² – b² = (a + b) (a – b)]
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ 5m + 3 = 0 or 5m – 3 = 0
∴ 5m = -3 or 5m = 3
∴ m = −35 or m = 35
∴ The roots of the given quadratic equation are −35 and 35.

xi. 7m² = 21m
∴ 7m² – 21m = 0
∴ m² – 3m = 0 …[Dividing both sides by 7]
∴ m(m – 3) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ m = 0 or m – 3 = 0
∴ m = 0 or m = 3
∴ The roots of the given quadratic equation are 0 and 3.

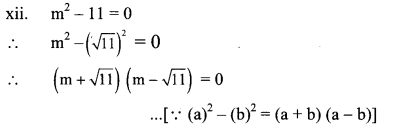
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ m + √11 = 0 or m – √11 = 0
∴ m = -√11 or m = √11
∴ The roots of the given quadratic equation are – √11 and √11

Practice Set 2.3

Question 1.
Solve the following quadratic equations by completing the square method.
1. x² + x – 20 = 0
2. x² + 2x – 5 = 0
3. m² – 5m = -3
4. 9y² – 12y + 2 = 0
5. 2y² + 9y + 10 = 0
6. 5x² = 4x + 7
Solution:
1. x² + x – 20 = 0
If x² + x + k = (x + a)², then
x² + x + k = x² + 2ax + a²
Comparing the coefficients, we get
1 = 2a and k = a²

∴ The roots of the given quadratic equation are 4 and -5.

2. x² + 2x – 5 = 0
If x² + 2x + k = (x + a)², then
x² + 2x + k = x² + 2ax + a²
Comparing the coefficients, we get
2 = 2a and k = a²
∴ a = 1 and k = (1)² = 1
Now, x² + 2x – 5 = 0
∴ x² + 2x + 1 – 1 – 5 = 0
∴ (x + 1)² – 6 = 0
∴ (x + 1)² = 6
Taking square root of both sides, we get
x + 1 = ± √6
∴ x + 1 √6 or x + 1 = √6
∴ x = √6 – 1 or x = -√6 – 1
∴ The roots of the given quadratic equation are √6 -1 and – √6 -1.

3. m² – 5m = -3
∴ m² – 5m + 3 = 0
If m² – 5m + k = (m + a)², then
m² – 5m + k = m² + 2am + a²
Comparing the coefficients, we get
-5 = 2a and k = a²

4. 9y² – 12y + 2 = 0

5. 2y² + 9y + 10 = 0

Taking square root of both sides, we get

∴ The roots of the given quadratic equation are -2 and −52.

6. 5x² = 4x + 7
∴ 5x² – 4x – 7 = 0

Comparing the coefficients, we get

Practice Set 2.4

Question 1.
Compare the given quadratic equations to the general form and write values of a, b, c.
i. x² – 7x + 5 = 0
ii. 2m² = 5m – 5
iii. y² = 7y
Solution:
i. x² – 7x + 5 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = -7, c = 5

ii. 2m² = 5m – 5
∴ 2m² – 5m + 5 = 0
Comparing the above equation with
am² + bm + c = 0, we get
a = 2, b = -5, c = 5

iii. y² = 7y
∴ y² – 7y + 0 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 1, b = -7, c = 0

Question 2.
Solve using formula.
i. x² + 6x + 5 = 0
ii. x² – 3x – 2 = 0
iii. 3m² + 2m – 7 = 0
iv. 5m² – 4m – 2 = 0
v. y² + 13 y = 2
vi. 5x² + 13x + 8 = 0
Solution:
i. x² + 6x + 5 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = 6, c = 5
∴ b² – 4ac = (6)2 – 4 × 1 × 5
= 36 – 20 = 16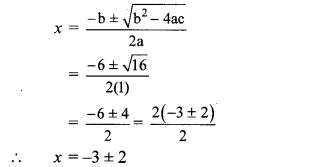

∴ x = -3 + 2 or x = -3 -2
∴ x = -1 or x = -5
∴ The roots of the given quadratic equation are -1 and -5.

ii. x² – 3x – 2 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = -3, c = -2
∴ b² – 4ac = (-3)2 – 4 × 1 × (-2)
= 9 + 8 = 17

iii. 3m² + 2m – 7 = 0
Comparing the above equation with
am² + bm + c = 0, we get
a = 3, b = 2, c = -7
∴ b² – 4ac = (2)² – 4 × 3 × ( -7)
= 4 + 84 = 88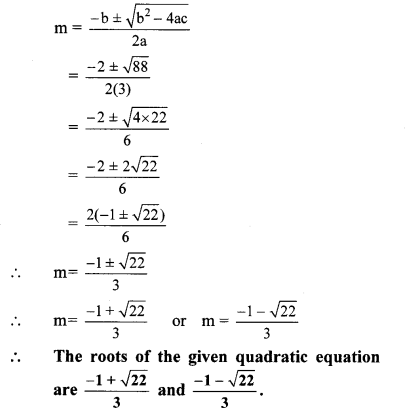

iv. 5m² – 4m – 2 = 0
Comparing the above equation with
am² + bm + c = 0, we get
a = 5, b = -4, c = -2
∴ b² – 4ac = (-4)² – 4 × 5 × (-2)
= 16 + 40 = 56

v. y² + 13y = 2
∴ 3y² + y = 6 …(Multiplying both sides by 3]
∴ 3y² + y – 6 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 3, b = 1, c = -6
∴ b² – 4ac = (1)² – 4 × 3 × (-6)
= 1 + 72 = 73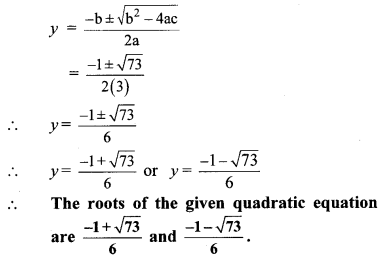

vi. 5x² + 13x + 8 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 5, b = 13, c = 8
∴ b² – 4ac = (13)2 – 4 × 5 × 8
= 169 – 160 = 9


The roots of the given quadratic equation are -1 and −85.

Question 3.
With the help of the flow chart given below solve the equation x² + 2√3 x + 3 = 0 using the formula.

Solution:
i. x² + 2√3 x + 3 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = 2√3 ,c = 3

ii. b² – 4ac = (2√3)2 -4 × 1 × 3
= 12 – 12
= 0

Question 1.
Solve the equation 2x² + 13x + 15 = 0 by factorisation method, by completing the square method and by using the formula. Verify that you will get the same roots every time. (Textbook pg. no. 43)
Solution: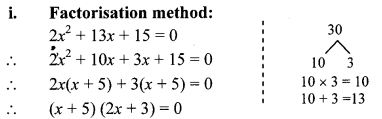

By using the property, if the product of two numbers is zero, then at least zero, we get
∴ x + 5 = 0 or 2x + 3 = 0
∴ x + -5 = 0 or 2x = -3 = 0
∴ x + -5 = or x = −32
∴ The roots of the given quadratic equation are −32 and -5.

ii. Completing the square method:
2x² + 13x + 15 = 0


∴ The roots of the given quadratic equation are −32 and -5.

iii. Formula method:
2x² + 13x + 15 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 2, b = 13, c = 15
∴ b² – 4ac = (13)2 – 4 × 2 × 15
= 169 – 120 = 49

∴ The roots of the given quadratic equation are −32 and -5.
∴ By all the above three methods, we get the same roots of the given quadratic equation.

Practice Set 2.5

Question 1.
Fill in the gaps and complete.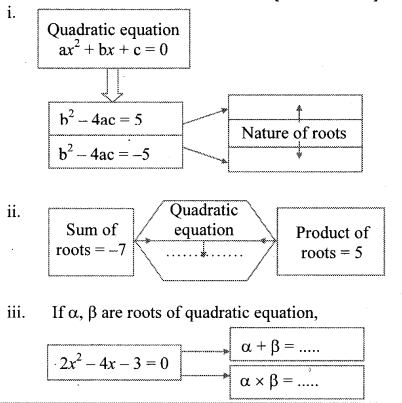

Answer: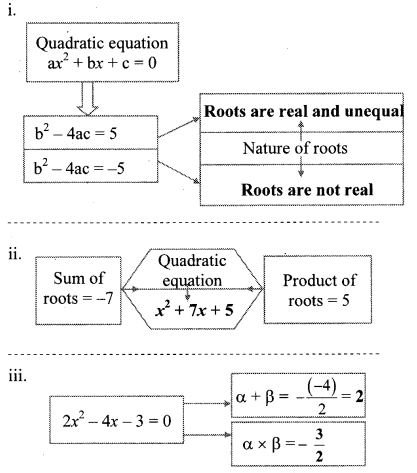

Question 2.
Find the value of discriminant.
i. x² + 7x – 1 = 0
ii. 2y² – 5y + 10 = 0
iii. √2 x² + 4x + 2√2 = 0
Solution:
i. x² +7 x – 1 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = 7, c = -1
∴ b²– 4ac = (7)² – 4 × 1 × (-1)
= 49 + 4
∴ b² – 4ac = 53

ii. 2y² – 5y + 10 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 2, b = -5, c = 10
∴ b² – 4ac = (-5)2 -4 × 2 × 10
= 25 – 80
∴ b² – 4ac = -55

iii. √2 x² + 4x + 2√2 = 0
Comparing the above equation with
ax + bx + c = 0, we get
a = √2,b = 4, c = 2√2
∴ b² – 4ac = (4)2 – 4 × √2 × 2√2
= 16 – 16
∴ b² – 4ac =0

Question 3.
Determine the nature of roots of the following quadratic equations.
i. x² – 4x + 4 = 0
ii. 2y² – 7y + 2 = 0
iii. m² + 2m + 9 = 0
Solution:
i. x² – 4x + 4= 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1,b = -4, c = 4
∴ ∆ = b² – 4ac
= (- 4)² – 4 × 1 × 4
= 16 – 16
∴ ∆ = 0
∴ Roots of the given quadratic equation are real and equal.

ii. 2y² – 7y + 2 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 2, b = -7, c = 2
∴ ∆ = b² – 4ac
= (- 7)² – 4 × 2 × 2
= 49 – 16
∴ ∆ = 33
∴ ∆ > 0
∴ Roots of the given quadratic equation are real and unequal.

iii. m² + 2m + 9 = 0
Comparing the above equation with
am² + bm + c = 0, we get
a = 1,b = 2, c = 9
∴ ∆ = b² – 4ac
= (2)² – 4 × 1 × 9
= 4 – 36
∴ ∆ = -32
∴ ∆ < 0
∴ Roots of the given quadratic equation are not real.

Question 4.
Form the quadratic equation from the roots given below.
i. 0 and 4
ii. 3 and -10
iii. 12 , 12
iv. 2 – √5, 2 + √5
Solution:
i. Let a = 0 and β = 4
∴ α + β = 0 + 4 = 4
and α × β = 0 × 4 = 0
∴ The required quadratic equation is
x² – (α + β) x + αβ = 0
∴ x² – 4x + 0 = 0
∴ x² – 4x = 0

ii. Let α = 3 and β = -10
∴ α + β = 3 – 10 = -7
and α × β = 3 × -10 = -30
∴ The required quadratic equation is
x² – (α + β)x + αβ = 0
∴ x² – (-7) x + (-30) = 0

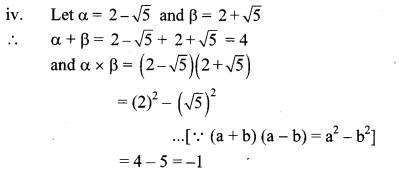
∴ The required quadratic equation is
x² – (α + β)x + αβ = 0
∴ x² – 4x – 1 = 0

Question 5.
Sum of the roots of a quadratic equation is double their product. Find k if equation is x² – 4kx + k + 3 = 0.
Solution:
x² – 4kx + k + 3 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = – 4k, c = k + 3
Let α and β be the roots of the given quadratic equation.
Then, α + β  = −ba and αβ = ca
According to the given condition,

Question 6.
α, β are roots of y² – 2y – 7 = 0 find,
i. α² + β²
ii. α³ + β³
Solution:
y² – 2y – 7 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 1, b = -2, c = -7

Question 7.
The roots of each of the following quadratic equations are real and equal, find k.
i. 3y² + ky + 12 = 0
ii. kx (x-2) + 6 = 0
Solution:
i. 3y² + kg + 12 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 3, b = k, c = 12
∴ ∆ = b² – 4ac
= (k)² – 4 × 3 × 12
= k² – 144 = k² – (12)²
∴ ∆ = (k + 12) (k – 12) …[∵ a² – b² = (a + b) (a – b)]
Since, the roots are real and equal.
∴ ∆ = 0
∴ (k + 12) (k – 12) = 0
∴ k + 12 = 0 or k – 12 = 0
∴ k = -12 or k = 12

ii. kx (x – 2) + 6 = 0
∴ kx² – 2kx + 6 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = k, b = -2k, c = 6
∴ ∆ = b² – 4ac
= (-2k)² – 4 × k × 6
= 4k² – 24k
∴ ∆ = 4k (k – 6)
Since, the roots are real and equal.
∴ ∆ = 0
∴ 4k (k – 6) = 0
∴ k(k – 6) = 0
∴ k = 0 or k – 6 = 0
But, if k = 0 then quadratic coefficient becomes zero.
∴ k ≠ 0
∴ k = 6

Question 1.
Fill in the blanks. (Textbook pg. no. 44)
Solution:

Question 2.
Determine nature of roots of the quadratic equation: x² + 2x – 9 = 0 (Textbook pg. no. 45)
Solution:

∴ The roots of the given equation are real and unequal.

Question 3.
Fill in the empty boxes properly. (Textbook pg. no. 46)
Solution:
10x² + 10x + 1 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 10, b = 10, c = 1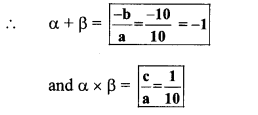

Question 4.
Write the quadratic equation if addition of the roots is 10 and product of the roots is 9. (Textbook pg, no. 48)
Answer:

Question 5.
What will be the quadratic equation if α = 2, β = 5. (Textbook pg. no, 48)
Solution: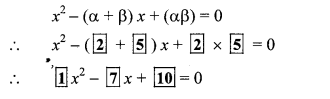

Practice Set 2.6 

Question 1.
Product of Pragati’s age 2 years ago and years hence is 84. Find her present age.
Solution:
Let the present age of Pragati be x years.
∴ 2 years ago,
Age of Pragati = (x – 2) years
After 3 years,
Age of Pragati = (x + 3) years
According to the given condition,
(x – 2) (x + 3) = 84
∴ x(x + 3) – 2(x + 3) = 84
∴ x² + 3x – 2x – 6 = 84
∴ x² + x – 6 – 84 = 0
∴ x² + x – 90 = 0
x² + 10x – 9x – 90 = 0
∴ x(x + 10) – 9(x + 10) = 0
∴ (x + 10)(x – 9) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 10 = 0 or x – 9 = 0
∴ x = -10 or x = 9
But, age cannot be negative.
∴ x = 9
∴ Present age of Pragati is 9 years.

Question 2.
The sum of squares of two consecutive even natural numbers is 244; find the numbers.
Solution:
Let the first even natural number be x.
∴ the next consecutive even natural number will be (x + 2).
According to the given condition,
x² + (x + 2)2 = 244
∴ x² + x² + 4x + 4 = 244
∴ 2x² + 4x + 4 – 244 = 0
∴ 2x² + 4x – 240 = 0
∴ x² + 2x – 120 = 0 …[Dividing both sides by 2]
∴ x² + 12x – 10x – 120 = 0
∴ x(x + 12) – 10 (x + 12) = 0
∴ (x + 12) (x – 10) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 12 = 0 or x – 10 = 0
∴ x = -12 or x = 10
But, natural number cannot be negative.
∴ x = 10 and x + 2 = 10 + 2 = 12
∴ The two consecutive even natural numbers are 10 and 12.

Question 3.
In the orange garden of Mr. Madhusudan there are 150 orange trees. The number of trees in each row is 5 more than that in each column. Find the number of trees in each row and each column with the help of following flow chart.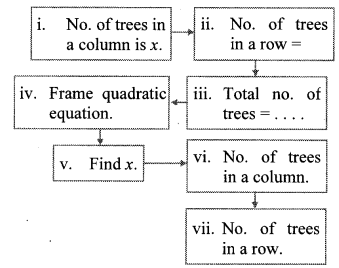

Solution:
i. Number of trees in a column is x.
ii. Number of trees in a row = x + 5
iii. Total number of trees = x x (x + 5)
iv. According to the given condition,
x(x + 5) = 150
∴ x² + 5x = 150
∴ x² + 5x – 150 = 0
v. x² + 15x – 10x – 150 = 0
∴ x(x+ 15) – 10(x + 15) = 0
∴ (x + 15)(x – 10) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 15 = 0 or x – 10 = 0
∴ x = -15 or x = 10
But, number of trees cannot be negative.
∴ x = 10
vi. Number of trees in a column is 10.
vii. Number of trees in a row = x + 5 = 10 + 5 = 15
∴ Number of trees in a row is 15.

Question 4.
Vivek is older than Kishor by 5 years. The Find their present ages is 16 Find their Present ages
Solution:
Let the present age of Kishor be x.
∴ Present age of Vivek = (x + 5) years
According to the given condition,

∴ 6(2x + 5) = x(x + 5)
∴ 12x + 30 = x2 + 5x
∴ x² + 5x – 12x – 30 = 0
∴ x² – 7x – 30 = 0
∴ x² – 10x + 3x – 30 = 0
∴ x(x – 10) + 3(x – 10) = 0
∴ (x – 10)(x + 3) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 10 = 0 or x + 3 = 0
∴ x = 10 or x = – 3
But, age cannot be negative.
∴ x = 10 andx + 5 = 10 + 5 = 15
∴ Present ages of Kishor and Vivek are 10 years and 15 years respectively.

Question 5.
Suyash scored 10 marks more in second test than that in the first. 5 times the score of the second test is the same as square of the score in the first test. Find his score in the first test.
Solution:
Let the score of Suyash in the first test be x.
∴ Score in the second test = x + 10 According to the given condition,
5(x + 10) = x²
∴ 5x + 50 = x²
∴ x² – 5x – 50 = 0
∴ x² – 10x + 5x – 50 = 0
∴ x(x – 10) + 5(x – 10) = 0
∴ (x – 10) (x + 5) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 10 = 0 or x + 5 = 0
∴ x = 10 or x = – 5
But, score cannot be negative.
∴ x = 10
∴ The score of Suyash in the first test is 10.

Question 6.
‘Mr. Kasam runs a small business of making earthen pots. He makes certain number of pots on daily basis. Production cost of each pot is ₹ 40 more than 10 times total number of pots, he makes in one day. If production cost of all pots per day is ₹ 600, find production cost of one pot and number of pots he makes per day.
Solution:
Let Mr. Kasam make x number of pots on daily basis.
Production cost of each pot = ₹ (10x + 40)
According to the given condition,
x(10x + 40) = 600
∴ 10x² + 40x = 600
∴ 10x² + 40x- 600 = 0
∴ x² + 4x – 60 = 0 …[Dividing both sides by 10]
∴ x² + 10x – 6x – 60 = 0
∴ x(x + 10) – 6(x + 10) = 0
∴ (x + 10) (x – 6) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 10 = 0 or x – 6 = 0
∴ x = – 10 or x = 6
But, number of pots cannot be negative.
∴ x = 6
∴ Production cost of each pot = 7(10 x + 40)
= ₹ [(10×6)+ 40]
= ₹(60 + 40) = ₹ 100
Production cost of one pot is ₹ 100 and the number of pots Mr. Kasam makes per day is 6.

Question 7.
Pratik takes 8 hours to travel 36 km downstream and return to the same spot. The speed of boat in still water is 12 km. per hour. Find the speed of water current.
Solution:
Let the speed of water current be x km/hr. Speed of boat is 12 km/hr. (x < 12)
In upstream, speed of the water current decreases the speed of the boat and it is the opposite in downstream.
∴ speed of the boat in upstream = (12 – x) km/hr and speed of the boat in downstream = (12 + x) km/hr.

∴ The speed of water current is 6 km/hr.

Question 8.
Pintu takes 6 days more than those of Nishu to complete certain work. If they work together they finish it in 4 days. How many days would it take to complete the work if they work alone.
Solution:
Let Nishu take x days to complete the work alone.
∴ Total work done by Nishu in 1 day = 1x
Also, Pintu takes (x + 6) days to complete the work alone.
∴ Total work done by Pintu in 1 day = 1x+6
∴ Total work done by both in 1 day = (1x + 1x+6)
But, both take 4 days to complete the work together.
∴ Total work done by both in 1 day = 14
According to the given condition,

∴ 4(2x + 6) = x(x + 6)
∴ 8x + 24 = x² + 6x
∴ x² + 6x – 8x – 24 = 0
∴ x² – 2x – 24 = 0
∴ x² – 6x + 4x – 24 = 0
∴ x(x – 6)+ 4(x – 6) = 0
∴ (x – 6) (x + 4) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 6 = 0 or x + 4 = 0
∴ x = 6 or x = -4
But, number of days cannot be negative,
∴ x = 6 and x + 6 = 6 + 6 = 12
∴ Number of days taken by Nishu and Pintu to complete the work alone is 6 days and 12 days respectively.

Question 9.
If 460 is divided by a natural number, quotient is 6 more than five times the divisor and remainder is 1. Find quotient and divisor.
Solution:
Let the natural number be x.
∴ Divisor = x, Quotient = 5x + 6
Also, Dividend = 460 and Remainder = 1
Dividend = Divisor × Quotient + Remainder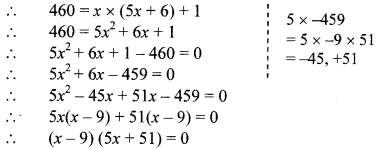

By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 9 = 0 or 5x + 51 = 0
∴ x = 9 or x = −515
But, natural number cannot be negative,
∴ x = 9
∴ Quotient = 5x + 6 = 5(9) + 6 = 45 + 6 = 51
∴ Quotient is 51 and Divisor is 9.

Question 10.
In the given fig. []ABCD is a trapezium, AB || CD and its area is 33 cm2. From the information given in the figure find the lengths of all sides of the []ABCD. Fill in the empty boxes to get the solution.

Solution:

By using the property, if the product of two numbers is zero, then at least one of them is zero, we get

Download PDF

Maharashtra Board Solutions for Class 10-Maths (Part 1): Chapter 2- Quadratic Equations

Download PDF: Maharashtra Board Solutions for Class 10-Maths (Part 1): Chapter 2- Quadratic Equations PDF

Chapterwise Maharashtra Board Solutions Class 10 Maths (Part 1) :

• Chapter 1- Linear Equations in Two Variables
• Chapter 2- Quadratic Equations
• Chapter 3- Arithmetic Progression
• Chapter 4- Financial Planning
• Chapter 5- Probability
• Chapter 6- Statistics

FAQs

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC. 

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.

Read More

• RD Sharma Solutions for Class 10 Maths Chapter 8–Quadratic Equations
• NCERT Solutions for Class 10th Mathematics: Chapter 4 Quadratic Equations
• RS Aggarwal Solutions for Class 10 Maths Chapter 4–Quadratic Equations
• NCERT Solutions for Class 8 Maths
• NCERT Solutions for Class 7 Maths

IndCareer Board Book Solutions App

IndCareer Board Book App provides complete study materials for students from classes 1 to 12 of Board. The App contains complete solutions of NCERT books, notes, and other important materials for students. Download the IndCareer Board Book Solutions now.