Class 6: Maths Chapter 22 solutions. Complete Class 6 Maths Chapter 22 Notes.
Contents
Selina Class 6 ICSE Solutions Mathematics : Chapter 22- Simple (Linear) Equations
Selina 6th Maths Chapter 22, Class 6 Maths Chapter 22 solutions
Exercise 22(A)
1. Solve:
(i) x + 2 = 6
(ii) x + 6 = 2
(iii) y + 8 = 5
(iv) x + 4 = – 3
(v) y + 2 = – 8
Solution:
(i) x + 2 = 6
x = 6 – 2
We get,
x = 4
Hence, the value of x for x + 2 is 4
(ii) x + 6 = 2
x = 2 – 6
We get,
x = = – 4
Hence, the value of x for x + 6 = 2 is – 4
(iii) y + 8 = 5
y = 5 – 8
We get,
y = – 3
Hence, the value of y for y + 8 = 5 is – 3
(iv) x + 4 = – 3
x = – 3 – 4
We get,
x = – 7
Hence, the value of x for x + 4 = – 3 is – 7
(v) y + 2 = – 8
y = – 8 – 2
We get,
y = – 10
Hence, the value of y for y + 2 = – 8 is – 10
2. Solve:
(i) x – 3 = 2
(ii) m – 2 = – 5
(iii) b – 5 = 7
(iv) a – 2.5 = – 4
(v) y – 3 (1 / 2) = 6
Solution:
(i) x – 3 = 2
x = 2 + 3
We get,
x = 5
Therefore, the value of x for x – 3 = 2 is 5
(ii) m – 2 = – 5
m = – 5 + 2
We get,
m = – 3
Therefore, the value of m for m – 2 = – 5 is – 3
(iii) b – 5 = 7
b = 7 + 5
We get,
b = 12
Therefore, the value of b for b – 5 = 7 is 12
(iv) a – 2. 5 = – 4
a = – 4 + 2. 5
We get,
a = – 1. 5
Therefore, the value of a for (a – 2. 5) = – 4 is – 1. 5
(v) y – 3 (1 / 2) = 6
This can be written as,
y – (7 / 2) = 6
y = 6 + (7 / 2)
y = (12 + 7) / 2
y = 19 / 2
y =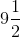
Therefore, the value of y for y – 3 (1 / 2) = 6 is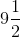
3. Solve:
(i) 3x = 12
(ii) 2y = 9
(iii) 5z = 8.5
(iv) 2.5m = 7.5
(v) 3.2p = 16
Solution:
(i) 3x = 12
x = 12 / 3
We get,
x = 4
Hence, the value of x for 3x = 12 is 4
(ii) 2y = 9
y = 9 / 2
We get,
y = 4.5
Hence, the value of y for 2y = 9 is 4.5
(iii) 5z = 8.5
z = 8.5 / 5
We get.
z = 1.7
Hence, the value of z for 5z = 8.5 is 1.7
(iv) 2.5m = 7.5
m = 7.5 / 2.5
We get,
m = 3
Hence, the value of m for 2.5m = 7.5 is 3
(v) 3.2p = 16
p = 16 / 3.2
p = (16 × 10) / 32
p = 160 / 32
p = 5
Hence, the value of p for 3.2p = 16 is 5
4. Solve:
(i) x / 2 = 5
(ii) y / 3 = – 2
(iii) a / 5 = – 15
(iv) z / 4 = 3 (1 / 4)
(v) m / 6 = 2 (1 / 2)
Solution:
(i) x / 2 = 5
x = 5 × 2
We get,
x = 10
Hence, the value of x for x / 2 = 5 is 10
(ii) y / 3 = – 2
y = – 2 × 3
We get,
y = – 6
Hence, the value of y for y / 3 = – 2 is – 6
(iii) a / 5 = – 15
a = – 15 × 5
We get,
a = – 75
Hence, the value of a for a / 5 = – 15 is – 75
(iv) z / 4 = 3 (1 / 4)
This can be written as,
z / 4 = 13 / 4
z = 13 / 4 × 4
We get,
z = 13
Hence, the value of z for z / 4 = 3 (1 / 4) is 13
(v) m / 6 = 2 (1 / 2)
This can be written as,
m / 6 = 5 / 2
m = 5 / 2 × 6
m = 5 × 3
We get,
m = 15
Hence, the value of m for m / 6 = 2 (1 / 2) is 15
5. Solve:
(i) – 2x = 8
(ii) – 3.5y = 14
(iii) – 5z = 4
(iv) – 5 = a + 3
(v) 2 = p + 5
Solution:
(i) – 2x = 8
x = – 8 / 2
We get,
x = – 4
Therefore, the value of x for – 2x = 8 is – 4
(ii) – 3.5y = 14
y = – 14 / 3. 5
We get,
y = – 4
Therefore, the value of y for – 3.5y = 14 is – 4
(iii) – 5z = 4
z = – 4 / 5
We get,
z = – 0.8
Therefore, the value of z for – 5z = 4 is – 0.8
(iv) – 5 = a + 3
– 5 – 3 = a
On calculating, we get
a = – 8
Therefore, the value of a for – 5 = a + 3 is – 8
(v) 2 = p + 5
2 – 5 = p
We get,
p = – 3
Therefore, the value of p for 2 = p + 5 is – 3
Exercise 22(B)
1. Solve:
(i) 2x + 5 = 17
(ii) 3y – 2 = 1
(iii) 5p + 4 = 29
(iv) 4a – 3 = – 27
(v) 2z + 3 = – 19
Solution:
(i) 2x + 5 = 17
2x = 17 – 5
2x = 12
x = 12 / 2
We get,
x = 6
Therefore, the value of x = 6
(ii) 3y – 2 = 1
3y = 1 + 2
3y = 3
y = 3 / 3
We get,
y = 1
Therefore, the value of y = 1
(iii) 5p + 4 = 29
5p = 29 – 4
5p = 25
p = 25 / 5
We get,
p = 5
Therefore, the value of p = 5
(iv) 4a – 3 = – 27
4a = – 27 + 3
4a = – 24
a = – 24 / 4
We get,
a = – 6
Therefore, the value of a = – 6
(v) 2z + 3 = – 19
2z = – 19 – 3
2z = – 22
z = – 22 / 2
We get,
z = – 11
Therefore, the value of z = – 11
2. Solve:
(i) x / 3 – 5 = 2
(ii) y / 2 – 3 = 8
(iii) z / 7 + 1 = 2 (1 / 2)
(iv) a / 2.4 – 5 = 2.4
(v) b / 1.6 + 3 = – 2.5
Solution:
(i) x / 3 – 5 = 2
x / 3 = 2 + 5
x / 3 = 7
x = 7 × 3
We get,
x = 21
Hence, the value of x = 21
(ii) y / 2 – 3 = 8
y / 2 = 8 + 3
y / 2 = 11
y = 11 × 2
We get,
y = 22
Hence, the value of y = 22
(iii) z / 7 + 1 = 2 (1 / 2)
This can be written as,
z / 7 + 1 = 5 / 2
z / 7 = 5 / 2 – 1
z / 7 = (5 – 2) / 2
We get,
z / 7 = 3 / 2
z = (3 / 2) × 7
On calculating, we get
z = 21 / 2
z =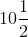
Hence, the value of z =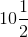
(iv) a / 2.4 – 5 = 2.4
a / 2.4 = 2.4 + 5
a / 2.4 = 7.4
a = 7.4 × 2.4
We get,
a = 17.76
Hence, the value of a = 17.76
(v) b / 1.6 + 3 = – 2.5
b / 1.6 = – 2.5 – 3
b / 1.6 = -5.5
b = – 5.5 × 1.6
We get,
b = – 8.8
Hence, the value of b = – 8.8
3. Solve:
(i) – 8m – 2 = – 10
(ii) 4x + 2x = 3 + 5
(iii) 4x – x + 5 = 8
(iv) 6x + 2 = 2x + 10
(v) 18 – (2a – 12) = 8a
Solution:
(i) – 8m – 2 = – 10
– 8m = – 10 + 2
– 8m = – 8
m = – 8 / – 8
We get,
m = 1
Therefore, the value of m = 1
(ii) 4x + 2x = 3 + 5
6x = 8
x = 8 / 6
We get,
x = 4 / 3
x =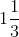
Therefore, the value of x =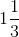
(iii) 4x – x + 5 = 8
3x = 8 – 5
3x = 3
x = 3 / 3
We get,
x = 1
Therefore, the value of x = 1
(iv) 6x + 2 = 2x + 10
6x – 2x = 10 – 2
On further calculation, we get
4x = 8
x = 8 /4
x = 2
Therefore, the value of x = 2
(v) 18 – (2a – 12) = 8a
18 – 2a + 12 = 8a
30 = 8a + 2a
30 = 10a
a = 30 / 10
We get,
a = 3
Therefore, the value of a = 3
Exercise 22(C)
1. 5 – x = 3
Solution:
Given equation is,
5 – x = 3
– x = 3 – 5
– x = – 2
We get,
x = 2
Hence, the value of x = 2
2. 2 – y = 8
Solution:
Given equation is,
2 – y = 8
– y = 8 – 2
We get,
y = – 6
Hence, the value of y = – 6
3. 8.4 – x = – 2
Solution:
Given equation is,
8.4 – x = – 2
– x = – 2 – 8.4
– x = – 10.4
We get,
x = 10.4
Hence, the value of x = 10.4
4. x + 2 (1 / 5) = 3
Solution:
Given equation is,
x + 2 (1 / 5) = 3
This can be written as,
x + 11 / 5 = 3
x = 3 – 11 / 5
Taking L.C.M, we get
x = (15 – 11) / 5
x = 4 / 5
Hence, the value of x = 4 / 5
5. y – 3(1 / 2) = 2(1 / 3)
Solution:
Given equation is,
y – 3(1 / 2) = 2(1 / 3)
This can be written as,
y – 7 / 2 = 7 / 3
y = 7 / 3 + 7 / 2
Taking L.C.M. we get,
y = (14 + 21) / 6
y = 35 / 6
y =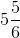
Hence, the value of y =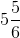
6. 5(2 / 3) – z = 2(1 / 2)
Solution:
Given equation is,
5(2 / 3) – z = 2(1 / 2)
This can be written as,
17 / 3 – z = 5 / 2
17 / 3 – 5 / 2 = z
z = 17 / 3 – 5 / 2
Taking L.C.M. we get,
z = (34 – 15) / 6
z = 19 / 6
z =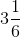
Hence, the value of z =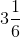
7. 1.6z = 8
Solution:
Given equation is,
1.6z = 8
z = 8 / 1.6
z = (8 × 10) / 16
z = (1 × 10) / 2
We get,
z = 5
Hence, the value of z = 5
8. 3a = – 2.1
Solution:
Given equation is,
3a = – 2. 1
a = – 2.1 / 3
a = – 21 / (3 × 10)
We get,
a = – 7 / 10
a = – 0.7
Hence, the value of a = – 0.7
9. z / 4 = – 1.5
Solution:
Given equation is,
z / 4 = – 1. 5
z = – 1.5 × 4
We get,
z = – 6
Hence, the value of z = – 6
10. z / 6 =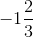
Solution:
Given equation is,
z / 6 =
This can be written as,
z / 6 = – 5 / 3
z = – 5 / 3 × 6
z = – 5 × 2
We get,
z = – 10
Hence, the value of z = – 10
11. – 5x = 10
Solution:
Given equation is,
– 5x = 10
x = 10 / – 5
We get,
x = – 2
Hence, the value of x = – 2
12. 2.4z = – 4.8
Solution:
Given equation is,
2.4z = = – 4.8
z = – 4.8 / 2.4
z = – 48 / 24
We get,
z = – 2
Hence, the value of z = – 2
13. 2y – 5 = – 11
Solution:
Given equation is,
2y – 5 = – 11
2y = – 11 + 5
2y = – 6
We get,
y = – 6 / 2
y = – 3
Hence, the value of y = – 3
14. 2x + 4.6 = 8
Solution:
Given equation is,
2x + 4.6 = 8
2x = 8 – 4.6
2x = 3.4
x = 34 / (2 × 10)
We get,
x = 17 / 10
x = 1.7
Hence, the value of x = 1.7
15. 5y – 3.5 = 10
Solution:
Given equation is,
5y – 3.5 = 10
5y = 10 + 3.5
5y = 13.5
y = 13.5 / 5
y = 135 / (5 × 10)
We get,
y = 27 / 10
y = 2.7
Hence, the value of y = 2.7
Exercise 22(D)
1. A number increased by 17 becomes 54. Find the number.
Solution:
Let us assume the number is x
Hence,
x + 17 = 54
x = 54 – 17
We get,
x = 37
Therefore, the required number is 37
2. A number decreased by 8 equals 26, find the number.
Solution:
Let us assume the number is x
Hence,
x – 8 = 26
x = 26 + 8
We get,
x = 34
Therefore, the required number is 34
3. One-fourth of a number add to two-seventh of it gives 135; find the number.
Solution:
Let us assume the number is x
Hence,
(1 / 4) × x + (2 / 7) × x = 135
(x / 4) + (2x / 7) = 135
Taking L.C.M. we get,
(7x + 8x) / 28 = 135
15x = 135 × 28
x = (135 × 28) / 15
We get,
x = 9 × 28
x = 252
Therefore, the required number is 252
4. Two-fifths of a number subtracted from three-fourths of it gives 56, find the number.
Solution:
Let us assume the number is x
(3 / 4) x – (2 / 5) x = 56
(3x / 4) – (2x / 5) = 56
Taking L.C.M. we get,
(15x – 8x) / 20 = 56
7x = 56 × 20
x = (56 × 20) / 7
We get,
x = 8 × 20
x = 160
Therefore, the required number is 160
5. A number is increased by 12 and the new number obtained is multiplied by 5. If the resulting number is 95, find the original number.
Solution:
Let us assume the number is x
Hence,
(x + 12) 5 = 95
5x + 60 = 95
5x = 95 – 60
5x = 35
x = 35 / 5
We get,
x = 7
Therefore, the original number is 7
6.A number is increased by 26 and the new number obtained is divided by 3. If the resulting number is 18; find the original number.
Solution:
Let us assume the number is x
Hence,
(x + 26) ÷ 3 = 18
This can be written as,
(x + 26) / 3 = 18
(x + 26) = 18 × 3
x + 26 = 54
x = 54 – 26
We get,
x = 28
Therefore, the original number is 28
7. The age of a man is 27 years more than the age of his son. If the sum of their ages is 47 years, find the age of the son and his father.
Solution:
Given
Age of a man is 27 years more than the age of his son
Sum of their ages = 47 years
Let us assume the age of son is x
Hence,
Age of son = x years
Age of father = x + 27
To find the value of x,
x + x + 27 = 47
2x + 27 = 47
2x = 47 – 27
2x = 20
x = 20 / 2
We get,
x = 10
Thus age of son = 10 years
Age of father = x + 27
Substituting the value of x, we get
= 10 + 27
= 37 years
Hence, the age of father is 37 years.
Therefore, the age of son is 10 years and the age of father is 37 years
8. The difference between the ages of Gopal and his father is 26 years. If the sum of their ages is 56 years, find the ages of Gopal and his father.
Solution:
Given
Difference between the ages of Gopal and his father is 26 years
Sum of their ages = 56 years
Let us assume the age of Gopal is x
Hence,
Age of Gopal = x
Age of father = x + 26
To find the value of x
x + x + 26 = 56
2x = 56 – 26
2x = 30
x = 30 / 2
We get,
x = 15
Thus the age of Gopal is 15 years
Age of father = x + 26
Substituting the value of x, we get
= 15 + 26
= 41 years
Hence, the age of father is 41 years
Therefore, the age of Gopal is 15years and the age of his father is 41 years
9. When two consecutive natural numbers are added, the sum is 31; find the numbers.
Solution:
Given
Two consecutive natural numbers sum is 31
Let us assume the first natural number is x
Hence,
First number = x
Second number = x + 1
To find the value of x,
x + x + 1 = 31
2x = 31 – 1
2x = 30
x = 30 / 2
We get,
x = 15
Thus the first number is 15
Second number = x + 1
Substituting the value of x, we get
= 15 + 1
= 16
Hence, the second number is 16
Therefore, the first natural number is 15 and the second natural number is 16
10. When three consecutive natural numbers are added, the sum is 66, find the numbers.
Solution:
Given
Three consecutive natural numbers sum = 66
Let us assume the first natural number is x
Hence,
First number = x
Second number = x + 1
Third number = x + 2
Now, calculation to find the value of x,
x + x + 1 + x + 2 = 66
3x + 3 = 66
3x = 66 – 3
3x = 63
x = 63 / 3
We get,
x = 21
Hence,
First number = x
= 21
Second number = x + 1
= 21 + 1
= 22
Third number = x + 2
= 21 + 2
= 23
Therefore, three consecutive natural numbers are 21, 22 and 23
11. A natural number decreased by 7 is 12. Find the number.
Solution:
Let us assume the natural number is x
Hence,
x – 7 = 12
x = 12 + 7
We get,
x = 19
Therefore, the required number is 19
12. One-fourth of a number added to one-sixth of itself is 15. Find the number.
Solution:
Let us assume the number is x
Hence,
(1 / 4) × x + (1 / 6) × x = 15
x / 4 + x / 6 = 15
Taking L.C.M. we get,
(3x + 2x) / 12 = 15
5x = 15 × 12
x = (15 × 12) / 5
x = 3 × 12
We get,
x = 36
Therefore, the required number is 36
13. A whole number is increased by 7 and the new number so obtained is multiplied by 5; the result is 45. Find the number.
Solution:
Let us assume the whole number is x
Hence,
(x + 7) 5 = 45
5x + 35 = 45
5x = 45 – 35
We get,
5x = 10
x = 10 / 5
We get,
x = 2
Therefore, the required whole number is 2
14. The age of a man and the age of his daughter differ by 23 years and the sum of their ages is 41 years. Find the age of the man.
Solution:
Given
Difference between the ages of a man and his daughter = 23 years
Sum of their ages = 41 years
Let us assume the age of a daughter is x
Hence,
Age of a man = x + 23
Now, calculating to find the value of x,
x + x + 23 = 41
2x + 23 = 41
2x = 41 – 23
2x = 18
x = 18 / 2
We get,
x = 9
Hence,
Age of a man = x + 23
= 9 + 23
= 32
Therefore, the age of a man is 32 years
15. The difference between the ages of a woman and her son is 19 years and the sum of their ages is 37 years; find the age of the son.
Solution:
Given
Difference between the ages of a woman and her son = 19 years
Sum of their ages = 37 years
Let us assume the age of a son is x
Hence,
Age of woman = x + 19
Now, calculating to find the value of x,
x + x + 19 = 37
2x + 19 = 37
2x = 37 – 19
2x = 18
x = 18 / 2
We get,
x = 9
Therefore, the age of her son is 9 years
Download PDF
Selina Class 6 ICSE Solutions Mathematics : Chapter 22- Simple (Linear) Equations
Download PDF: Selina Class 6 ICSE Solutions Mathematics : Chapter 22- Simple (Linear) Equations PDF
Chapterwise Selina Publishers ICSE Solutions for Class 6 Mathematics :
- Chapter 1- Number System
- Chapter 2- Estimation
- Chapter 3- Numbers In Indian And International Systems
- Chapter 4- Place Value
- Chapter 5- Natural Numbers And Whole Numbers
- Chapter 6- Negative Numbers And Integers
- Chapter 7- Number Line
- Chapter 8- HCF And LCM
- Chapter 9- Playing With Numbers
- Chapter 10- Sets
- Chapter 11- Ratio
- Chapter 12- Proportion
- Chapter 13- Unitary Method
- Chapter 14- Fractions
- Chapter 15- Decimal Fractions
- Chapter 16- Percent (Percentage)
- Chapter 17- Idea of Speed, Distance and Time
- Chapter 18- Fundamental Concepts
- Chapter 19- Fundamental Operations
- Chapter 20- Substitution
- Chapter 21- Framing Algebraic Expressions (Including Evaluation)
- Chapter 22- Simple (Linear) Equations
- Chapter 23- Fundamental Concepts
- Chapter 24- Angles
- Chapter 25- Properties of Angles and Lines
- Chapter 26- Triangles
- Chapter 27- Quadrilateral
- Chapter 28- Polygons
- Chapter 29- The Circle
- Chapter 30- Revision Exercise Symmetry
- Chapter 31- Recognition of Solids
- Chapter 32- Perimeter and Area of Plane Figures
- Chapter 33- Data Handling
- Chapter 34- Mean and Median
About Selina Publishers ICSE
Selina Publishers has been serving the students since 1976 and is one of the quality ICSE school textbooks publication houses. Mathematics and Science books for classes 6-10 form the core of our business, apart from certain English and Hindi literature as well as a few primary books. All these books are based upon the syllabus published by the Council for the I.C.S.E. Examinations, New Delhi. The textbooks are composed by a panel of subject experts and vetted by teachers practising in ICSE schools all over the country. Continuous efforts are made in complying with the standards and ensuring lucidity and clarity in content, which makes them stand tall in the industry.
