Selina Class 6 ICSE Solutions Mathematics : Chapter 20- Substitution

Class 6: Maths Chapter 20 solutions. Complete Class 6 Maths Chapter 20 Notes.

Selina Class 6 ICSE Solutions Mathematics : Chapter 20- Substitution

Selina 6th Maths Chapter 20, Class 6 Maths Chapter 20 solutions

Exercise 20(A)

1. Fill in the following blanks, when:

x = 3, y = 6, z = 18, a = 2, b = 8, c = 32 and d = 0.

(i) x + y = ……….

(ii) y – x = ……….

(iii) y / x = ………..

(iv) c ÷ b = ………..

(v) z ÷ x = ………..

Solution:

(i) x + y = ……..

The value of x + y is calculated as shown below

x + y = 3 + 6

= 9

∴ x + y = 9

(ii) y – x = ……….

The value of y – x is calculated as shown below

y – x = 6 – 3

= 3

∴ y – x = 3

(iii) y / x = ………..

The value of y / x is calculated as shown below

y / x= 6 / 3

= 2

∴ y / x = 2

(iv) c ÷ b = ………

The value of c ÷ b is calculated as shown below

c ÷ b = 32 ÷ 8

32 / 8 = 4

∴ c ÷ b = 4

(v) z ÷ x = ……….

The value of z ÷ x is calculated as shown below

z ÷ x = 18 ÷ 3

= 6

∴ z ÷ x = 6

2. Find the value of:

(i) p + 2q + 3r, when p = 1, q = 5 and r = 2

(ii) 2a + 4b + 5c, when a = 5, b = 10 and c = 20

(iii) 3a – 2b, when a = 8 and b = 10

(iv) 5x + 3y – 6z, when x = 3, y = 5 and z = 4

(v) 2p – 3q + 4r – 8s, when p = 10, q = 8, r = 6 and s = 2

Solution:

(i) p + 2q + 3r, when p = 1, q = 5 and r = 2

The value of p + 2q + 3r is calculated as shown below

p + 2q + 3r = 1 + 2 × 5 + 3 × 2

= 1 + 10 + 6

= 17

Therefore, p + 2q + 3r = 17

(ii) 2a + 4b + 5c, when a = 5, b = 10 and c = 20

The value of 2a + 4b + 5c is calculated as shown below

2a + 4b + 5c = 2 × 5 + 4 × 10 + 5 × 20

= 10 + 40 + 100

= 150

Therefore, 2a + 4b + 5c = 150

(iii) 3a – 2b, when a = 8 and b = 10

The value of 3a – 2b is calculated as shown below

3a – 2b = 3 × 8 – 2 × 10

= 24 – 20

= 4

Therefore, 3a – 2b = 4

(iv) 5x + 3y – 6z, when x = 3, y = 5 and z = 4

The value of 5x + 3y – 6z is calculated as shown below

5x + 3y – 6z = 5 × 3 + 3 × 5 – 6 × 4

= 15 + 15 – 24

= 30 – 24

= 6

Therefore, 5x + 3y – 6z = 6

(v) 2p – 3q + 4r – 8s, when p = 10, q = 8, r = 6 and s = 2

The value of 2p – 3q + 4r – 8s is calculated as shown below

2p – 3q + 4r – 8s = 2 × 10 – 3 × 8 + 4 × 6 – 8 × 2

= 20 – 24 + 24 – 16

= 4

Therefore, 2p – 3q + 4r – 8s = 4

3. Find the value of:

(i) 4pq × 2r, when p = 5, q = 3 and r = 1 / 2

(ii) yx / z, when x = 8, y = 4 and z = 16

(iii) (a + b – c) / 2a, when a = 5, b = 7 and c = 2

Solution:

(i) 4pq × 2r, when p = 5, q = 3 and r = 1 / 2

The value of 4pq × 2r is calculated as below

4pq × 2r = 4 × 5 × 3 × 2 × (1 / 2)

= 4 × 5 × 3

= 60

∴ 4pq × 2r = 60

(ii) yx / z, when x = 8, y = 4 and z = 16

The value of yx / z is calculated as below

yx / z = (4 × 8) / 16

= 32 / 16

= 2

∴ yx / z = 2

(iii) (a + b – c) / 2a, when a = 5, b = 7 and c = 2

The value of (a + b – c) / 2a is calculated as below

(a + b – c) / 2a = (5 + 7 – 2) / (2 × 5)

= 10 / 10

= 1

4. If a = 3, b = 0, c = 2 and d = 1, find the value of:

(i) 3a + 2b – 6c + 4d

(ii) 6a – 3b – 4c – 2d

(iii) ab – bc + cd – da

(iv) abc – bcd + cda

(v) a² + 2b² – 3c²

Solution:

(i) 3a + 2b – 6c + 4d

The value of 3a + 2b – 6c + 4d is calculated as shown below

3a + 2b – 6c + 4d = 3 × 3 + 2 × 0 – 6 × 2 + 4 × 1

On further calculation, we get

= 9 + 0 – 12 + 4

= 9 – 12 + 4

= 13 – 12

= 1

Therefore, 3a + 2b – 6c + 4d = 1

(ii) 6a – 3b – 4c – 2d

The value of 6a – 3b – 4c – 2d is calculated as shown below

6a – 3b – 4c – 2d = 6 × 3 – 3 × 0 – 4 × 2 – 2 × 1

On further calculation, we get

= 18 – 0 – 8 – 2

= 18 – 10

= 8

Therefore, 6a – 3b – 4c – 2d = 8

(iii) ab – bc + cd – da

The value of ab – bc + cd – da is calculated as shown below

ab – bc + cd – da = 3 × 0 – 0 × 2 + 2 × 1 – 1 × 3

On further calculation, we get

= 0 – 0 + 2 – 3

= 2 – 3

= – 1

Therefore, ab – bc + cd – da = – 1

(iv) abc – bcd + cda

The value of abc – bcd + cda is calculated as shown below

abc – bcd + cda = 3 × 0 × 2 – 0 × 2 × 1 + 2 × 1 × 3

On further calculation, we get

= 0 – 0 + 6

= 6

Therefore, abc – bcd + cda = 6

(v) a² + 2b² – 3c²

The value of a² + 2b² – 3c² is calculated as shown below

a² + 2b² – 3c² = (3)² + 2 × (0)² – 3 × (2)²

On further calculation, we get

= 9 + 0 – 12

= 9 – 12

= – 3

Therefore, a² + 2b² – 3c² = – 3

5. Find the value of 5x² – 3x + 2, when x = 2

Solution:

The value of 5x² – 3x + 2 when x = 2 is calculated as below

5x² – 3x + 2 = 5 × (2)² – 3 × (2) + 2

On simplification, we get

= 5 × 4 – 3 × 2 + 2

= 20 – 6 + 2

= 22 – 6

= 16

Hence, the value of 5x² – 3x + 2 when x = 2 is 16

6. Find the value of 3x³ – 4x² + 5x – 6, when x = – 1

Solution:

The value of 3x³ – 4x² + 5x – 6 when x = -1 is calculated as below

3x³ – 4x² + 5x – 6 = 3 × (- 1)³ – 4 × (- 1)² + 5 × (- 1) – 6

On simplification, we get

= – 3 – 4 – 5 – 6

= – 18

Hence, the value of 3x³ – 4x² + 5x – 6 when x = – 1 is – 18

7. Show that the value of x³ – 8x² + 12x – 5 is zero, when x = 1

Solution:

The value of x³ – 8x² + 12x – 5 = 0 when x = 1 is calculated as below

x³ – 8x² + 12x – 5 = (1)³ – 8 × (1)² + 12 × (1) – 5

On simplification, we get

= 1 – 8 × 1 + 12 × 1 – 5

= 1 – 8 + 12 – 5

= 0

The value of x³ – 8x² + 12x – 5 = 0 when x = 1

Hence, proved

8. State true and false:

(i) The value of x + 5 = 6, when x = 1

(ii) The value of 2x – 3 = 1, when x = 0

(iii) (2x – 4) / (x + 1) = -1, when x = 1

Solution:

(i) The value of x + 5 = 6, when x = 1

The value of x + 5 = 6 for x = 1 is calculated as below

x + 5 = 6

Adding the value of x = 1, we get

1 + 5 = 6

6 = 6

Therefore, the given statement is true

(ii) The value of 2x – 3 = 1, when x = 0

The value of 2x – 3 = 1 for x = 0 is calculated as below

2x – 3 = 1

Adding the value of x = 0, we get

2(0) – 3 = 1

0 – 3 = 1

– 3 = 1

Therefore, the given statement is false

(iii) (2x – 4) / (x + 1) = -1, when x = 1

The value of (2x – 4) / (x + 1) = -1 for x = 1 is calculated as below

(2x – 4) / (x + 1) = -1

Adding x = 1, we get

2(1) – 4 / (1 + 1) = – 1

– 2 / 2 = – 1

– 1 = – 1

Therefore, the given statement is true

9. If x = 2, y = 5 and z = 4, find the value of each of the following:

(i) x / 2x²

(ii) xz / yz

(iii) z^x

(iv) y^x

(v) x²y²z² / xz

Solution:

(i) x / 2x²

The value of x / 2x² for x = 2, y = 5 and z = 4 is calculated as below

x / 2x²

Now, adding x = 2, y = 5 and z = 4, we get

x / 2x² = 2 / 2(2)²

On calculation, we get

= 2 / 8

= 1 / 4

(ii) xz / yz

The value of xz / yz for x = 2, y = 5 and z = 4 is calculated as below

xz / yz

Now, adding x = 2, y = 5 and z = 4, we get

xz / yz = (2) (4) / (5) (4)

On calculation, we get

= 8 / 20

= 2 / 5

(iii) z^x

The value of z^x for x = 2, y = 5 and z = 4 is calculated as below

Now, adding x = 2 and z = 4, we get

z^x = (4)²

We get

= 4 × 4

= 16

(iv) y^x

The value of y^x for x = 2, y = 5 and z = 4 is calculated as below

Now, adding x = 2 and y = 5, we get

y^x = (5)²

We get,

= 5 × 5

= 25

(v) x²y²z² / xz

The value of x²y²z² / xz for x = 2, y = 5 and z = 4 is calculated as below

Now, adding x = 2, y = 5 and z = 4, we get

x²y²z² / xz = (2)² × (5)² × (4)² / (2 × 4)

We get,

= 2^2-1 × 5² × 4^2-1

= 2 × 5 × 5 × 4

= 200

10. If a = 3, find the values of a² and 2^a

Solution:

The value of a² and 2^a for a = 3 is calculated as below

a² = 3²

= 3 × 3

= 9

2^a = 2³

= 2 × 2 × 2

= 8

Hence, the values of a² = 9 and 2^a = 8

11. If m = 2, find the difference between the values of 4m³ and 3m⁴.

Solution:

The difference between the values of 4m³ and 3m⁴ for m = 2 is calculated as below

4m³ = 4 × (2)³

= 4 × 2 × 2 × 2

We get,

= 32

3m⁴ = 3 × (2)⁴

= 3 × 2 × 2 × 2 × 2

We get,

= 48

Therefore, the difference of 4m³ and 3m⁴ is calculated as,

3m⁴ – 4m³ = 48 – 32

= 16

Hence, the difference between the given values is 16

Exercise 20(B)

1. Evaluate:

(i) (23 – 15) + 4

(ii) 5x + (3x + 7x)

(iii) 6m – (4m – m)

(iv) (9a – 3a) + 4a

(v) 35b – (16b + 9b)

Solution:

(i) (23 – 15) + 4

The value of the given expression (23 – 15) + 4 is calculated as follows

(23 – 15) + 4 = 8 + 4

We get,

= 12

Hence, the value of the given expression (23 – 15) + 4 = 12

(ii) 5x + (3x + 7x)

The value of the expression 5x + (3x + 7x) is calculated as follows

5x + (3x + 7x) = 5x + 10x

We get,

= 15x

Hence, the value of the expression 5x + (3x + 7x) = 15x

(iii) 6m – (4m – m)

The value of the expression 6m – (4m – m) is calculated as follows

6m – (4m – m) = 6m – 3m

We get,

= 3m

Hence, the value of the expression 6m – (4m – m) = 3m

(iv) (9a – 3a) + 4a

The value of the expression (9a – 3a) + 4a is calculated as follows

(9a – 3a) + 4a = 6a + 4a

We get,

= 10a

Hence, the value of the expression (9a – 3a) + 4a = 10a

(v) 35b – (16b + 9b)

The value of the expression 35b – (16b + 9b) is calculated as follows

35b – (16b + 9b) = 35b – 25b

We get,

= 10b

Hence, the value of the expression 35b – (16b + 9b) = 10b

2. Simplify:

(i) 12x – (5x + 2x)

(ii) 10m + (4n – 3n) – 5n

(iii) (15b – 6b) – (8b + 4b)

(iv) – (- 4a – 8a)

(v) x – (x – y) – (- x + y)

Solution:

(i) 12x – (5x + 2x)

The simplified form of the expression 12x – (5x + 2x) is calculated as below

12x – (5x + 2x) = 12x – 7x

We get,

= 5x

(ii) 10m + (4n – 3n) – 5n

The simplified form of the expression 10m + (4n – 3n) – 5n is calculated as below

10m + (4n – 3n) – 5n = 10m + n – 5n

We get,

= 10m – 4n

(iii) (15b – 6b) – (8b + 4b)

The simplified form of the expression (15b – 6b) – (8b + 4b) is calculated as below

(15b – 6b) – (8b + 4b) = 9b – 12b

We get,

= – 3b

(iv) – (- 4a – 8a)

The simplified form of the expression – (- 4a – 8a) is calculated as below

– (- 4a – 8a) = – (- 12a)

We get,

= 12a

(v) x – (x – y) – (- x + y)

The simplified form of the expression x – (x – y) – (- x + y) is calculated as below

x – (x – y) – (- x + y) = x – x + y + x – y

We get,

= x

3. Simplify:

(i) x – (y – z) + x + (y – z) + y – (z + x)

(ii) x – [y + {x – (y + x)}]

(iii) 4x + 3 (2x – 5y)

(iv) 2 (3a – b) – 5 (a – 3b)

(v) p + 2 

Solution:

(i) x – (y – z) + x + (y – z) + y – (z + x)

The simplified form of the expression x – (y – z) + x + (y – z) + y – (z + x) is calculated as follows

x – (y – z) + x + (y – z) + y – (z + x) = x – y + z + x + y – z + y – z – x

We get,

= x + y – z

(ii) x – [y + {x – (y + x)}]

The simplified form of the expression x – [y + {x – (y + x)}] is calculated as follows

x – [y + {x – (y + x)}] = x – [y + {x – y – x}]

= x – [y + x – y – x]

= x – x + x – y + y

We get,

= x

(iii) 4x + 3 (2x – 5y)

The simplified form of the expression 4x + 3 (2x – 5y) is calculated as follows

4x + 3 (2x – 5y) = 4x + 6x – 15y

We get,

= 10x – 15y

(iv) 2 (3a – b) – 5 (a – 3b)

The simplified form of the expression 2 (3a – b) – 5 (a – 3b) is calculated as follows

2 (3a – b) – 5 (a – 3b) = 6a – 2b – 5a + 15b

We get,

= a + 13b

(v) p + 2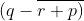 

The simplified form of the expression p + 2 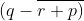is calculated as follows,

p + 2 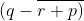= p + 2 (q – r – p)

= p + 2q – 2r – 2p

We get,

= 2q – 2r – p

Exercise 20(C)

1. Fill in the blanks:

(i) 2a + b – c = 2a + (………)

(ii) 3x – z + y = 3x – (………)

(iii) 6p – 5x + q = 6p – (…….)

(iv) a + b – c + d = a + (……..)

(v) 5a + 4b + 4x – 2c = 4x – (………)

Solution:

(i) 2a + b – c = 2a + (b – c)

(ii) 3x – z + y = 3x – (z – y)

(iii) 6p – 5x + q = 6p – (5x – q)

(iv) a + b – c + d = a + (b – c + d)

(v) 5a + 4b + 4x – 2c = 4x – (2c – 5a – 4b)

2. Insert the bracket as indicated:

(i) x – 2y = – (…………)

(ii) m + n – p = – (……..)

(iii) a + 4b – 4c = a + (……..)

(iv) a – 3b + 5c = a – (……..)

(v) x² – y² + z² = x² – (………)

Solution:

(i) x – 2y = – (2y – x)

(ii) m + n – p = – (p – m – n)

(iii) a + 4b – 4c = a + (4b – 4c)

(iv) a – 3b + 5c = a – (3b – 5c)

(v) x² – y² + z² = x² – (y² – z²)

Download PDF

Selina Class 6 ICSE Solutions Mathematics : Chapter 20- Substitution

Download PDF: Selina Class 6 ICSE Solutions Mathematics : Chapter 20- Substitution PDF

Chapterwise Selina Publishers ICSE Solutions for Class 6 Mathematics :

• Chapter 1- Number System
• Chapter 2- Estimation
• Chapter 3- Numbers In Indian And International Systems
• Chapter 4- Place Value
• Chapter 5- Natural Numbers And Whole Numbers
• Chapter 6- Negative Numbers And Integers
• Chapter 7- Number Line
• Chapter 8- HCF And LCM
• Chapter 9- Playing With Numbers
• Chapter 10- Sets
• Chapter 11- Ratio
• Chapter 12- Proportion
• Chapter 13- Unitary Method
• Chapter 14- Fractions
• Chapter 15- Decimal Fractions
• Chapter 16- Percent (Percentage)
• Chapter 17- Idea of Speed, Distance and Time
• Chapter 18- Fundamental Concepts
• Chapter 19- Fundamental Operations
• Chapter 20- Substitution
• Chapter 21- Framing Algebraic Expressions (Including Evaluation)
• Chapter 22- Simple (Linear) Equations
• Chapter 23- Fundamental Concepts
• Chapter 24- Angles
• Chapter 25- Properties of Angles and Lines
• Chapter 26- Triangles
• Chapter 27- Quadrilateral
• Chapter 28- Polygons
• Chapter 29- The Circle
• Chapter 30- Revision Exercise Symmetry
• Chapter 31- Recognition of Solids
• Chapter 32- Perimeter and Area of Plane Figures
• Chapter 33- Data Handling
• Chapter 34- Mean and Median

About Selina Publishers ICSE

Selina Publishers has been serving the students since 1976 and is one of the quality ICSE school textbooks publication houses. Mathematics and Science books for classes 6-10 form the core of our business, apart from certain English and Hindi literature as well as a few primary books. All these books are based upon the syllabus published by the Council for the I.C.S.E. Examinations, New Delhi. The textbooks are composed by a panel of subject experts and vetted by teachers practising in ICSE schools all over the country. Continuous efforts are made in complying with the standards and ensuring lucidity and clarity in content, which makes them stand tall in the industry.