RS Aggarwal Solutions for Class 9 Maths Chapter 4–Lines and Triangles

Class 9: Maths Chapter 4 solutions. Complete Class 9 Maths Chapter 4 Notes.

RS Aggarwal Solutions for Class 9 Maths Chapter 4–Lines and Triangles

RS Aggarwal 9th Maths Chapter 4, Class 9 Maths Chapter 4 solutions

Ex 4A Solutions

Question 1.
Solution:
(i)Angle : When two rays OA and OB meet at a point o, then ∠AOB is called an angle.

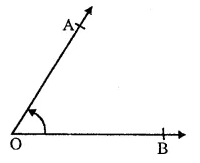
(ii) Interior of angle : The interior an angle is a set of all points in its plane which lie on the same side of OA as B and also on the same side of OB as A.
(iii) Obtuse angle : An angle greater than 90° but less than 180° is called an obtuse angle.
(iv) Reflex angle : An angle more than 180° but less than 360° is called a reflex angle.
(v) Complementary angles : Two angles are said to be complementary angles if their sum is 90°.
(vi) Supplementary angles : Two angles are said to be supplementary angles if their sum is 180°.

Question 2.
Solution:
∠A = 36°27’46”
∠B = 28° 43’39”
Adding, ∠A + ∠B = 64° 70′ 85″
We know that 60″ = 1′ and 60′ = 1°
∠A+ ∠B = 65° 11′ 25″ Ans.

Question 3.
Solution:
36° – 24° 28′ 30″
= 35° 59’60” – 25° 28’30”

= 10° 31′ 30″ Ans.

Question 4.
Solution:
We know that two angles are complementary of their sum is 90°. Each of these two angles is complement to the other, therefore.
(i) Complement of 58° = 90° – 58° = 32°
(ii) Complement of 16° = 90° – 16° = 74°
(iii) Complement of 23 of a right angle i.e.
of 23 x 90° or 60° = 90° – 60° = 30°
= 23 of right angle,
(iv) Complement of 46° 30′
= 90° – 46° 30′
= 43° 30′
(v) Complement of 52° 43′ 20°= 90° – 52° 43′ 20″
= 37° 16′ 40″
(vi) Complement of 68° 35′ 45″
= 90° – 68° 35′ 45″
= 21° 24′ 15″ Ans.

Question 5.
Solution:
We know that two angles are said to be supplement to each other of their sum is 180° therefore
(i) Supplement of 68° = 180° – 68° =112°
(ii) Supplement of 138° = 180° – 138° = 42°
(iii) Supplement of 35 of a right angle or 35 x 90° or 54°
= 180° – 54° = 126°
(iv) Supplement of 75° 36′ = 180° – 75° 36′ = 104° 24′
(v) Supplement of 124° 20′ 40″
= 180° – 124° 20′ 40″
= 55° 39′ 20″
(vi) Supplement of 108° 48′ 32″ = 180° – 108″ 48′ 32″ = 71° 11′ 28″ Ans.

Question 6.
Solution:
(i) Let the measure of required angle = x ,
their its complement = 90° – x
According to the condition,
x = 90° – x => 2x = 90°
=>x = 90o2 = 45°
Required angle = 45°
(ii) Let the measure of required angle = x then its supplement = 180° – x
According to the condition,
x = 180° – x => 2x = 180° = 90°
=>x = 180o2 = 90°
Hence required angle = 90° Ans.

Question 7.
Solution:
Let required angle = x
then its complement = 90° – x
According to the condition,
x – (90° – x) = 36°
=> x – 90° + x = 36°
=> 2x = 36° + 90° = 126°
= 126o2 = 63°
Required angle = 63° Ans.

Question 8.
Solution:
Let the required angle = x
then its supplement = 180° – x
According to the condition,
(180° – x) – x = 25°
=> 180° – x – x = 25°
=> – 2x = 25° – 180°
=> – 2x = – 155°
=> x = –155o–2
= 77.5°
Hence required angle = 77.5° Ans.

Question 9.
Solution:
Let required angle = x
Then its complement = 90° – x
According to the condition,
x = 4 (90° – x) => x = 360° – 4x
=> x + 4x = 360° => 5x = 360°
x = 360o5 = 72°
Required angle = 72° Ans.

Question 10.
Solution:
Let required angle = x
Then its supplement = 180° – x
According to the condition,
x = 5 (180° – x)
=> x = 900° – 5x
=> x + 5x = 900°
=> 6x = 900°
=> x = 900o6 = 150°
Hence, required angle = 150° Ans

Question 11.
Solution:
Let required angle = x
then its supplement = 180° – x
and complement = 90° – x
According to the condition,
180° – x = 4 (90°- x)
=> 180° – x = 360° – 4x
=> – x + 4x — 360° – 180°
=> 3x= 180°
=> x = 180o3 = 60°
Required angle = 60° Ans.

Question 12.
Solution:
Let required angle = x
Then, its complement = 90° – x
and its supplement = 180° – x
According to the condition,
90° – x = 13 (180° – x)
=> 90° – x = 60° – 13 x
=> 90° – 60° = x – 13 x
=> 23 x = 30° =>x = 30oX32 => x = 45° Ans.

Question 13.
Solution:
Let one angle = x
Then, its supplement = 180° – x
According to the condition,
x : (180° – x) = 3:2
=> x180o−x=32
=>2x = 3(180°- x)
=> 2x = 540° – 3x
=> 2x + 3x = 540°
=> 5x = 540° => x = 540o5 = 108°
Angle = 108° and its supplement = 180° – 108° = 72°
Hence, angles are 108° and 72° Ans.

Question 14.
Solution:
Let angle = x
Then, its complementary angle = 90° – x
According to the condition,
x : (90° – x) = 4 : 5
=> x90o−x=45
=> 5x = 4 (90° – x)
=> 5x = 360° – 4x
=> 5x + 4x = 360°
=> 9x = 360°
=> x = 360o9=40o
and its complement = 90° – 40° = 50°
Hence, angles are 40° and 50° Ans.

Question 15.
Solution:
Let the required angle = x
.’. its complement = 90° – x
and supplement = 180° – x
According to the condition,
7(90° – x) = 3(180° – x) – 10°
=> 630° – 7x = 3 (180° – x) – 10°
=> 630° – 7x = 540° – 3x – 10°
=> – 7x + 3x = 540° – 10° – 630°
– 4x = – 100°
x = −100o−4=25o
Hence required angle = 25° Ans.

Question 1.
Solution:
AOB is a straight line
∠AOC + ∠BOC = 180° (Linear pair)
=> 62° + x= 180°
=> x = 180° – 62°
=> x = 118°
Hence, x = 118° Ans.

Question 2.
Solution:
AOB is straight line
∠AOC + ∠COD + ∠DOB – 180°
=> (3x – 5)° + 55° + (x + 20)° = 180°
=> 3x – 5° + 55° + x + 20° = 180°
=> 4x – 5° + 75° = 180°
=> 4x + 70° = 180°
=> 4x = 180° – 70°
=> 4x = 110°
=> x=110o4=27.5o
Hence x = 27.5°
and ∠AOC = 3x – 5° = 3 x 27.5° – 5°
= 82.5° – 5° = 77.5°
∠BOD = x + 20° = 27.5° + 20°
= 47.5° Ans.

Question 3.
Solution:
AOB is a straight line
∠AOC + ∠COD + ∠DOB = 180°
{angles on the same side of line AB}
=> (3x + 7)° + (2x – 19)° + x = 180°
=> 3x + 7° + 2x – 19° + x = 180°
=> 6x – 12° – 180°
=> 6x = 180° + 12° = 192°
=> x=192o6=32o
Here x = 32°
∠AOC = 3x + 7° = 3 x 32° + 7°
= 96° + 7°= 103°
∠COD = 2x – 19° = 2 x 32° – 19°
= 64 – 19° = 45°
and ∠BOD = x = 32° Ans.

Question 4.
Solution:
In the given figure,
x + y + z = 180°
But x : y : z = 5:4:6
Let ∠XOP = x° – 5a
∠POQ =y° = 4a
and ∠QOY = z = 6a
then 5a + 4a + 6a = x + y + z = 180°
=> 15a = 180°
=> a = 180o15=12o
=> x = 5a = 5 x 12° = 60°
y = 4a = 4 x 12° = 48°
and z = 6x = 6 x 12° = 72° Ans.

Question 5.
Solution:
AOB will be a straight line
If ∠AOC + ∠COB = 180°
If (3x + 20)° + (4x – 36)° = 180°
If 3x + 20 + 4x – 36 = 180°
If 7x – 16 = 180°
If 7x = 180° + 16 = 196°
If x=196o7=28o
Hence, if x = 28°, then AOB will be a straight line.

Question 6.
Solution:
AB and CD intersect each other at O
AOC = ∠BOD and ∠BOC = ∠AOD (vertically opposite angles)
But ∠AOC = 50°
∠BOD = ∠AOC = 50°
But ∠AOC + ∠BOC = 180° (Linear pair)
=> 50° + ∠BOC = 180°
=> ∠BOC = 180° – 50° = 130°
∠AOD = ∠BOC = 130°
Hence,∠AOD = 30°,∠BOD = 50° and ∠BOC = 130° Ans.

Question 7.
Solution:
In the figure,
AB, CD and EF are coplanar lines intersecting at O.
∠AOF = ∠BOE
∠DOF = ∠COE and ∠BOD = ∠AOC (Vertically opposite angles)
x = y,
z = 50°
t = 90°
But AOF + ∠DOF + ∠BOD = 180° (Angles on the same side of a st. line)
=> x + 50° + 90° = 180°
=> x° + 140° + 180°
=> x = 180° – 140° = 40°
Hence, x = 40°, y = x = 40°, z = 50° and t = 90° Ans.

Question 8.
Solution:
Three coplanar lines AB, CD and EF intersect at a point O
∠AOD = ∠BOC
∠DOF = ∠COE
and ∠AOE = ∠BOF
(Vertically opposite angles)
But ∠AOD = 2x
∠BOC = 2x
and ∠BOF = 3x
∠AOE = 3x
and ∠COE = 5x
∠DOF = 5x
But ∠AOD + ∠DOF + ∠BOF + ∠BOC + ∠COE + ∠AOE = 360° (Angles at a point)
=> 2x + 5x + 3x + 2x + 5x + 3x = 360°
=> 20x = 360° => x = 360o20 = 18°
Hence x = 18°
∠AOD = 2x = 2 x 18° = 36°
∠COE = 5x = 5 x 18° = 90°
and ∠AOE = 3x = 3 x 18° = 54° Ans.

Question 9.
Solution:
AOB is a line and CO stands on it forming ∠AOC and ∠BOC
But ∠AOC : ∠BOC = 5:4
Let ∠AOC = 5x and ∠BOC = 4x
But ∠AOC + ∠BOC = 180° (Linear pair)
=> 5x + 4x = 180° => 9x = 180°
=> x = 180o9 = 20°
∠AOC = 5x = 5 x 20° = 100°
and ∠BOC = 4x = 4 x 20° = 80° Ans.

Question 10.
Solution:
Two lines AB and CD intersect each other at O and
∠AOC = 90°
∠AOC = ∠BOD
(Vertically opposite angles)
∠BOD = 90°
But ∠AOC + ∠BOC = 180° (Linear pair)
=> 90° + ∠BOC – 180°
=> ∠BOC = 180° – 90° = 90°
But ∠AOD = ∠BOC
(Vertically opposite angles)
∠AOD = 90°
Hence each of the remaining angle is 90°.

Question 11.
Solution:
Two lines AB and CD intersect each other at O and

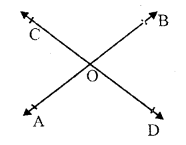
∠BOC + ∠AOD = 280°
∠AOD = ∠BOC
(vertically opposite angles)
∠BOC + ∠BOC = 280°
(∠AOD = ∠BOC)
=> 2 ∠BOC = 280°
=> ∠BOC = 280o2 = 140°
But ∠BOC + ∠AOC = 180° (Linear pair)
=> 140° + ∠AOC = 180°
=> ∠AOC = 180° – 140° = 40°
But ∠BOD = ∠AOC
(vertically opposite angles)
∠BOD = 40°
Hence ∠AOC = 40°, ∠BOC = 140°,
∠BOD = 40°
and ∠AOD = 140° Ans.

Question 12.
Solution:
OC is the bisector of ∠AOB. and OD is the ray opposite to OC.
Now ∠AOC = ∠BOC (OC is bisector of ∠AOB)
But ∠BOC + ∠BOD = 180° (Linear pair)
Similarly, ∠AOD + ∠AOC = 180°
=> ∠BOC + ∠BOD = ∠AOD + ∠AOC
But ∠AOC = ∠BOC (Given)
∠BOD = ∠AOD
=> ∠AOD = ∠BOD
Hence proved.

Question 13.
Solution:
AB is the mirror.
PQ is the incident ray, QR is its reflected ray.
=> ∠BQR = ∠PQA
But ∠BQR + ∠PQR + ∠PQA = 180° (Angles on one side of a straight line)
=> ∠PQA + ∠PQA + 112° = 180°
=> 2∠PQA + 112° = 180°
=> 2∠PQA = 180° – 112° = 68°
∠PQA = 68o2 = 34° Ans.

Question 14.
Solution:
Given. Two lines AB and CD intersect each other at O.
OE is the bisector of ∠BOD and EO is produced to F.
To Prove : OF bisects ∠AOC.
Proof : AB and CD intersect each other at O
∠AOC = ∠BOD
(Vertically opposite angles)
OE is the bisector of ∠BOD
∠1 = ∠2
But ∠1 = ∠3
and ∠2 = ∠4 (Vertically opposite angles)
and ∠1 = ∠2 (proved)
∠3 = ∠4
Hence, OF is the bisector of ∠AOC.
Hence proved.

Question 15.
Solution:
Given ∠AOC and ∠BOC are supplementary angles
OE is the bisector of ∠BOC and OF is the bisector of ∠AOC
To Prove : ∠EOF = 90°
Proof : ∠1 = ∠2
∠3 = ∠4
{OE and OF are the bisectors of ∠BOC and ∠AOC respectively}
But ∠AOC + ∠BOC = 180°
(Linear pair)
=> ∠1 + ∠2 + ∠3 + ∠4 = 180°
=> ∠1 + ∠1 + ∠3 + ∠3 = 180°
=> 2∠1 + 2∠3 = 180°
=> 2(∠1 + ∠3) = 180°
=> ∠1 + ∠3 = 180o2 90°
=> ∠EOF = 90°
Hence proved.

Question 1.
Solution:
AB || CD and a line t intersects them at E and F forming angles ∠1, ∠ 2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8.

Question 2.
Solution:
AB || CD and a transversal t intersects them at E and F respectively forming angles ∠l, ∠2, ∠3, ∠4, ∠5, ∠ 6, ∠ 7 and ∠ 8

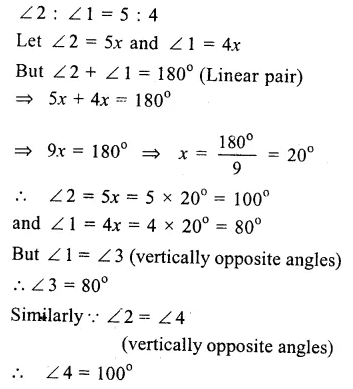
Question 3.
Solution:

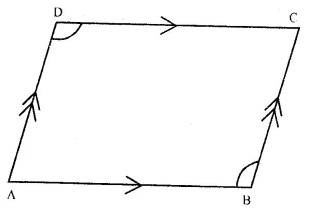
Given. In quadrilateral ABCD, AB || DC and AD || BC
To Prove : ∠ADC = ∠ABC
Proof : AB || DC and AD intersects their
∠DAB + ∠ADC = 180°
(sum of co-interior angles)
Similarly ∴ AD || BC
∠DAB + ∠ABC = 180° …(ii)
from (i) and (ii),
∠ DAB + ∠ ADC = ∠DAB + ∠ABC
∴∠ADC = ∠ABC. Hence proved.

Question 4.
Solution:
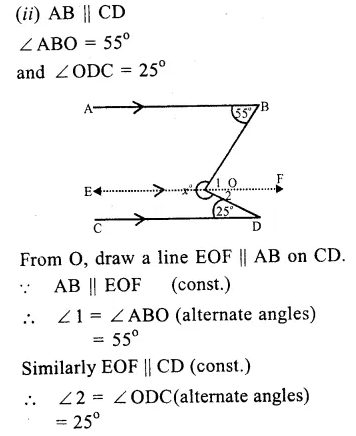
(i) In the figure, AB || CD
∠ABE = 35° and ∠EDC = 65°
Draw FEG || AB or CD
∴ AS || FG (const.)

Question 5.
Solution:
In the figure, AB || CD || EF,
∠ ABC = 70° and ∠ CEF = 130°
∴EF || CD (given)

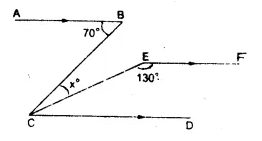
∴∠ CEF +∠1 – 180°
(sum of Co-interior angles)
=> 130° + ∠ 1 = 180°
=> ∠ 1 = 180° – 130° = 50°
Again, AB || CD (given)
∴ ∠ ABC = ∠ BCD (Alternate angles)
=> 70° = ∠ BCD = x + ∠ 1
=> x + 50° – 70°
=> x = 70° – 50° = 20°
Hence x = 20° Ans.

Question 6.
Solution:
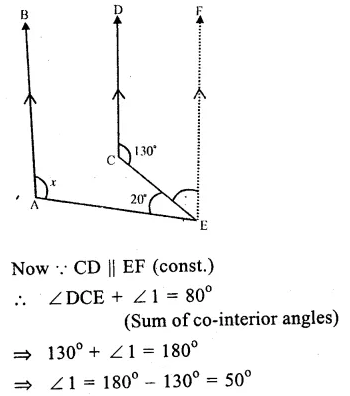
In the figure, AB || CD.
∠DCE = 130°
and ∠ CEA – 20°
From E, draw EF || AB or CD.

Question 7.
Solution:
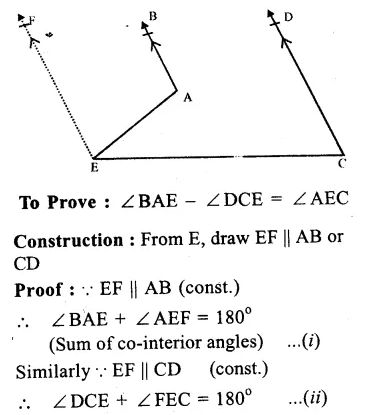
Given. In the given figure, AB || CD.

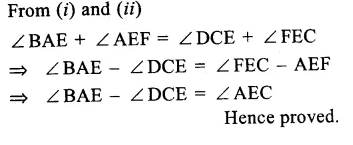
Question 8.
Solution:
In the figure, AB || CD

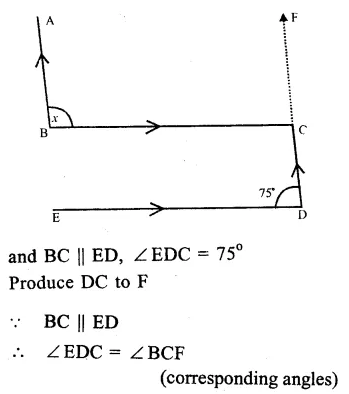
Question 9.
Solution:
In the figure, AB || CD, ∠AEF = p

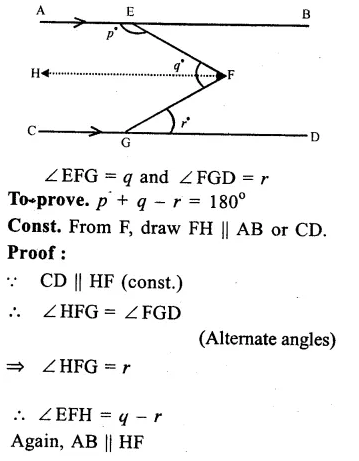
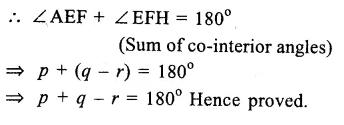
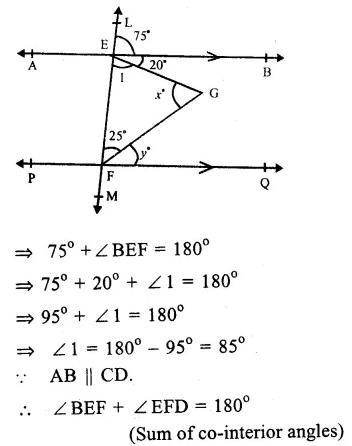
Question 10.
Solution:
In the figure, AB || PQ.
A transversal LM cuts them at E and F
∠ LEB = 75°
∠BEG = 20°
∠ EFG = 25°
∠ EGF = x° and ∠ GFD = y°
∴∠ LEB + ∠ BEF = 180° (Linear pair)

Question 11.
Solution:
In the figure

Question 12.
Solution:
In the figure, AB || CD
∠PEF = 85°, ∠QHC = 115°
∴ ∠ GHF = ∠ QHC
(Vertically opposite angles)
∠ GHF = 115°
∴AB || CD
∴∠ PEF = ∠ EGH
(Corresponding angles)
∴∠EGH = 85°
But ∠ QGH + ∠ EGH = 180°, (Linear pair)
=> ∠QGH + 85° = 180°
=> QGH = 180° – 85° = 95°
In ∆ GHQ,
Ext. ∠GHF = ∠QGH + ∠GQH
=> 115° = 95° + x
=> x = 115° – 95°
Hence, x = 20° Ans.

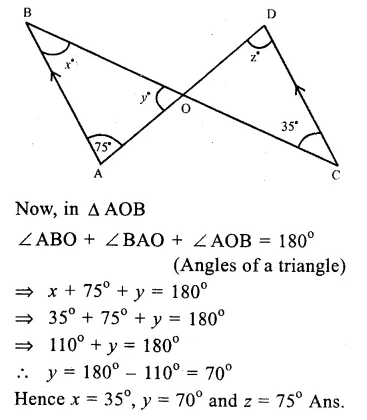
Question 13.
Solution:
In the figure, AB || CD
∠BAD = 75°, ∠ BCD = 35°
∴AB || CD
∴∠ABC = ∠BCD (Alternate angles)
=> x = 35°
and ∠ BAD = ∠ ADC (Alternate angles)
=> 75° = z

Question 14.
Solution:
In the figure, AB || CD
∠APQ = 75°, ∠ PRD = 125°
∴AB || CD.
∠ APQ = ∠ PQR (Alternate angles)
∴75° = y°
=> y° = 75°

Question 15.
Solution:
In the figure, AB || CD and EF || GH
∠APR = 110°, ∠LRF = 60°
∴∠PRQ = ∠LRF
(vertically opposite angles)

Question 16.
Solution:
(i) l is parallel to m
if 3x – 20° = 2x +10°
(Alternate angles are equal)

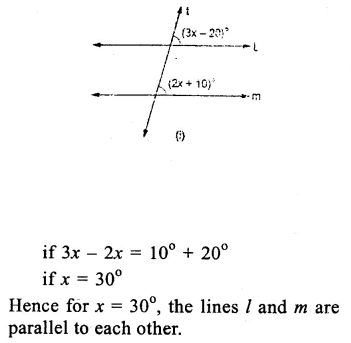
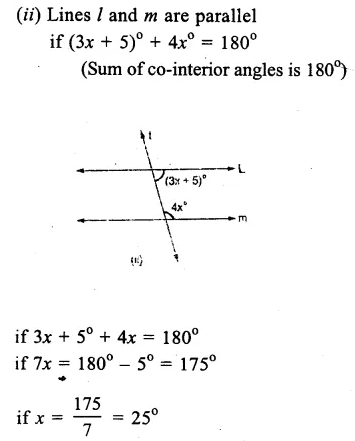
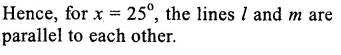
Question 17.
Solution:
Given. Two lines AB and CD are perpendiculars on EF
To Prove : AB ⊥ CD.

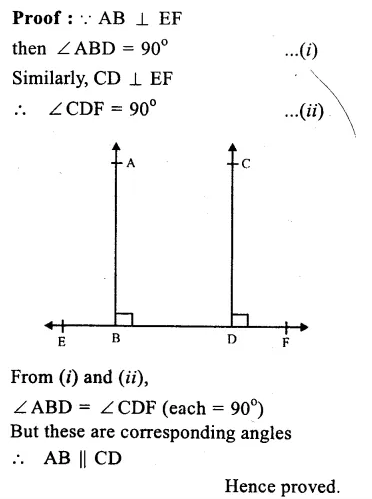
Question 1.
Solution:
In ∆ABC,
∠B = 76° and ∠C = 48°
But ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
=> ∠A + 76° + 48° = 180°
=> ∠ A + 124° = 180°
=> ∠A= 180° – 124° = 56°

Question 2.
Solution:
Angles of a triangle are in the ratio = 2:3:4
Let first angle = 2x
then second angle = 3x
and third angle = 4x
2x + 3x + 4x = 180°
(Sum of angles of a triangle)
=> 9x = 180°
=> x = 180o9 = 20°
First angle = 2x = 2 x 20° = 40°
Second angle = 3x = 3 x 20° = 60°
and third angle = 4x = 4 x 20° = 80° Ans.

Question 3.
Solution:
In ∆ABC,
3∠A = 4∠B = 6∠C = x (Suppose)

Question 4.
Solution:
In ∆ABC,
∠ A + ∠B = 108° …(i)
∠B + ∠C – 130° …(ii)
But ∠A + ∠B + ∠C = 180° …(iii)
(sum of angles of a triangle)
Subtracting (i) from (iii),
∠C = 180° – 108° = 72°
Subtracting (ii) from (iii),
∠A = 180°- 130° = 50°
But ∠ A + ∠B = 108° (from i)
50° + ∠B = 108°
=> ∠B = 108° – 50° = 58°
Hence ∠A = 50°, ∠B = 58° and ∠C = 72° Ans.

Question 5.
Solution:
In ∆ABC,
∠A+∠B = 125° …(i)
∠A + ∠C = 113° …(ii)
But ∠A + ∠B + ∠C = 180° …(iii)
(sum of angles of a triangles) Subtracting, (i), from (iii),
∠C = 180°- 125° = 55°
Subtracting (ii) from (iii),
∠B = 180°- 113° – 67°
∠A + ∠B = 125°
∠ A + 67° = 125°
=> ∠ A = 125° – 67°
∠A = 58°
Hence ∠A = 58°, ∠B = 67° and ∠ C = 55° Ans.

Question 6.
Solution:
In ∆ PQR,
∠ P – ∠ Q = 42°
=> ∠P = 42°+∠Q …(i)
∠Q – ∠R = 21°
∠Q – 21°=∠R …(ii)
But ∠P + ∠Q + ∠R = 180°
(Sum of angles of a triangles)
42° + ∠Q + ∠Q + ∠Q – 21°= 180°
=> 21° + 3∠Q = 180°
=> 3∠Q = 180°- 21° = 159°
from ∠Q = 159o3 = 53°
(i)∠P = 42° + ∠Q = 42° + 53° = 95°
and from (ii) ∠R = ∠Q – 21°
= 53° – 25° = 32°
Hence ∠P = 95°, ∠Q = 53° and ∠R = 32° Ans.

Question 7.
Solution:
Let ∠ A, ∠ B and ∠ C are the three angles of A ABC.
and ∠A + ∠B = 116° …(i)

Question 8.
Solution:
Let ∠ A, ∠ B and ∠ C are the three angles of the ∆ ABC
Let ∠ A = ∠ B = x
then ∠C = x + 48°
But ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
x + x + x + 18° = 180°
=> 3x + 18° = 180°
=> 3x = 180° – 18° = 162°
x = 162o3 = 54°
∠A = 54°, ∠B = 54° and ∠C = 54° + 18° = 72°
Hence angles are 54°, 54 and 72° Ans.

Question 9.
Solution:
Let the smallest angle of a triangle = x°
their second angle = 2x°
and third angle = 3x°
But sum of angle of a triangle = 180°
x + 2x + 3x = 180°
=> 6x = 180°
=> x – 180o6 = 30°
Hence smallest angle = 30°
Second angle = 2 x 30° = 60°
and third angle = 3 x 30° = 90° Ans.

Question 10.
Solution:
In a right angled triangle.
one angle is = 90°
Sum of other two acute angles = 90°
But one acute angle = 53°
Second acute angle = 90° – 53° = 37°
Hence angle of the triangle with be 90°, 53°, 37° Ans.

Question 11.
Solution:

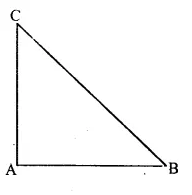
Given : In ∆ ABC,
∠ A = ∠B + ∠C
To Prove : ∆ABC is a right-angled
Proof : We know that in ∆ABC,
∠A + ∠B + ∠C = 180°
(angles of a triangle)
But ∠ A = ∠ B + C given
∠A + (∠B + ∠C) = 180°
=> ∠A + ∠A = 180°
=> 2∠A = 180°
=> ∠ A = 180o2 = 90°
∠ A = 90°
Hence ∆ ABC is a right-angled Hence proved.

Question 12.
Solution:
Given. In ∆ ABC, ∠A = 90°
AL ⊥ BC.

To Prove : ∠BAL = ∠ACB
Proof : In ∆ ABC, AL ⊥ BC
In right angled ∆ALC,
∠ ACB + ∠ CAL = 90° …(i)
( ∴∠L = 90°)
But ∠ A = 90° ‘
=> ∠ BAL + ∠ CAL = 90° …(ii)
From (i) and (ii),
∠BAL + ∠ CAL= ∠ ACB+ ∠CAL
=> ∠ BAL = ∠ ACB Hence proved.

Question 13.
Solution:
Given. In ∆ABC,
Each angle is less than the sum of the other two angles
∠A< ∠B + ∠C
∠B < ∠C + ∠A
and ∠C< ∠A + ∠C
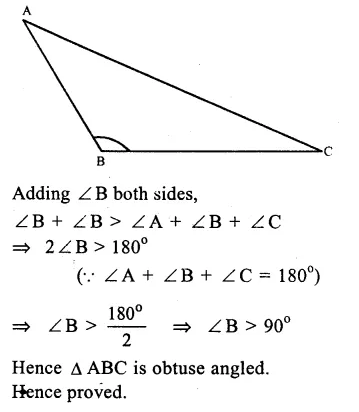
Proof : ∠ A < ∠B + ∠C
Adding ∠ A both sides,
∠A + ∠A < ∠A + ∠B + ∠C => 2 ∠ A < 180°
(∴ ∠A+∠B+∠C=180°)
∠A < 180o2 => ∠A< 90
Similarly, we can prove that,
∠B < 90° and ∠C < 90°
∴ each angle is less than 90°
Hence, triangle is an acute angled triangle. Hence proved.

Question 14.
Solution:
Given. In ∆ABC,
∠B > ∠A + ∠C

Question 15.
Solution:
In ∆ABC
∠ ABC = 43° and Ext. ∠ ACD = 128°

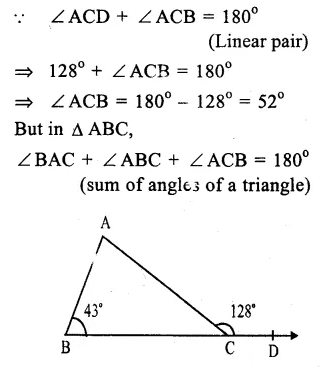
Question 16.
Solution:
∠ ABC + ∠ ABD = 180°
(Linear pair)

Question 17.
Solution:
(i)In the figure, ∠BAE =110° and ∠ACD = 120°.

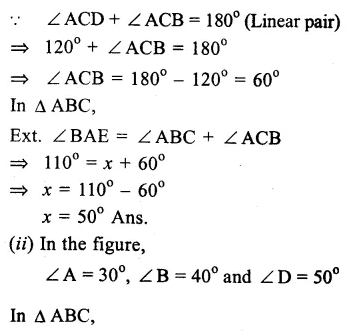
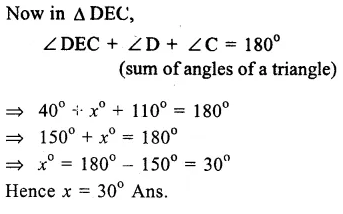
Question 18.
Solution:
In the figure,
∠A = 55°, ∠B = 45°, ∠C = 30° Join AD and produce it to E

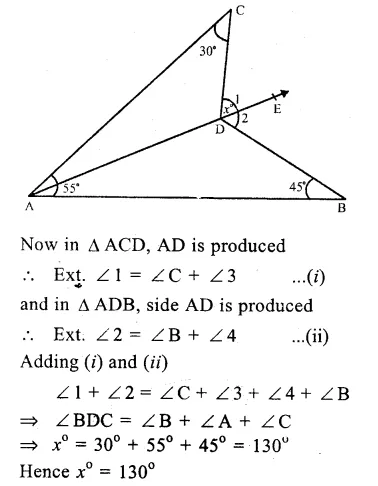
Question 19.
Solution:
In the figure,
∠EAC = 108°,
AD divides ∠ BAC in the ratio 1 : 3
and AD = DB
∠EAC + ∠ BAC = 180°
(Linear pair)

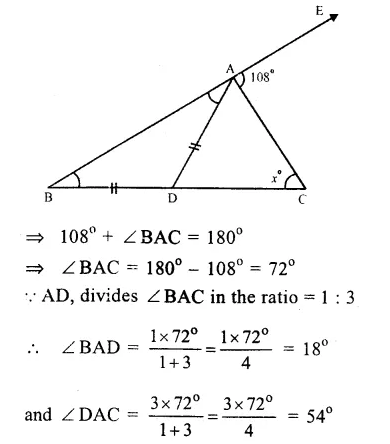
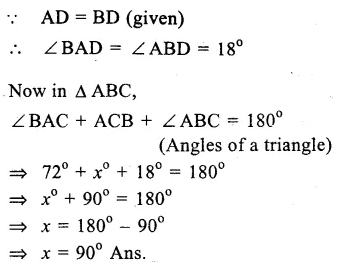
Question 20.

Solution:
Sides BC, CA and AB
are produced in order forming exterior
angles ∠ ACD,

Question 21.
Solution:
Given : Two ∆ s DFB and ACF intersect each other as shown in the figure.
To Prove : ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 360°
Proof : In ∆ DFB,
∠D + ∠F + ∠B = 180°
(sum of angles of a triangle)
Similarly,in ∆ ACE
∠A + ∠C + ∠E = 180° …(ii)
Adding (i) and (ii), we get :
∠D + ∠F + ∠B+ ∠A+ ∠C + ∠E = 180° + 180°
=> ∠A+∠B+∠C+∠D+∠E + ∠ F = 360°
Hence proved.

Question 22.
Solution:
In the figure,
ABC is a triangle
and OB and OC are the angle
bisectors of ∠ B and ∠ C meeting each other at O.
∠ A = 70°
In ∆ ABC,
∠A + ∠B + ∠C = 180°
(sum of angles of a triangle)

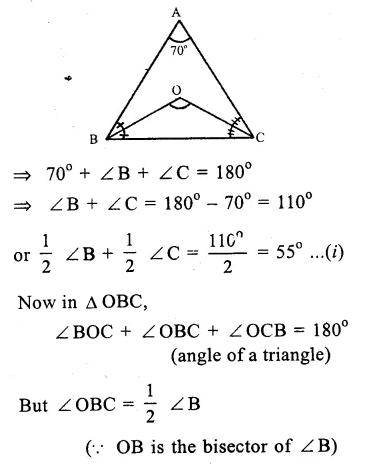
Question 23.
Solution:
In ∆ABC, ∠ A = 40°
Sides AB and AC are produced forming exterior angles ∠ CBD and ∠ BCE

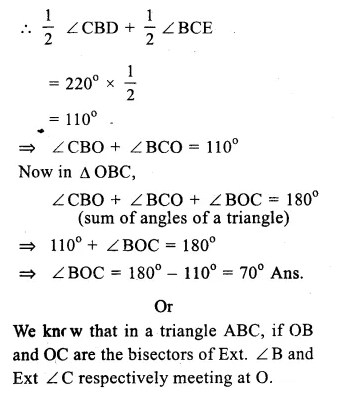
Question 24.
Solution:
In the figure, ∆ABC is triangle and ∠A : ∠B : ∠C = 3 : 2 : 1
AC ⊥ CD.
∠ A + ∠B + ∠C = 180°
(sum of angles of a triangle)
But ∠A : ∠B : ∠C = 3 : 2 : 1

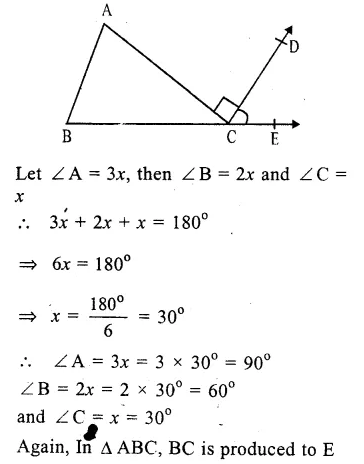
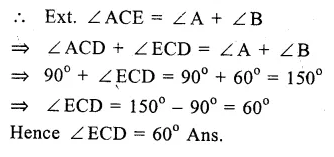
Question 25.
Solution:
In ∆ ABC
AN is the bisector of ∠ A
∠NAB =12 ∠A.
Now in right angled ∆ AMB,
∠B + ∠MAB = 90° (∠M = 90°)

Question 26.
Solution:
(i) False: As a triangle has only one right angle
(ii) True: If two angles will be obtuse, then the third angle will not exist.
(iii) False: As an acute-angled triangle all the three angles are acute.
(iv) False: As if each angle will be less than 60°, then their sum will be less than 60° x 3 = 180°, which is not true.
(v) True: As the sum of three angles will be 60° x 3 = 180°, which is true.
(vi) True: A triangle can be possible if the sum of its angles is 180°
But the given triangle having angles 10° + 80° + 100° = 190° is not possible.

RS Aggarwal Solutions for Class 9 Maths Chapter 4: Download PDF

RS Aggarwal Solutions for Class 9 Maths Chapter 4–Lines and Triangles

Download PDF: RS Aggarwal Solutions for Class 9 Maths Chapter 4–Lines and Triangles PDF

Chapterwise RS Aggarwal Solutions for Class 9 Maths :

• Chapter 1–Real Numbers
• Chapter 2–Polynomials
• Chapter 3–Introduction to Euclid’s Geometry
• Chapter 4–Lines and Triangles
• Chapter 5–Congruence of Triangles and Inequalities in a Triangle
• Chapter 6–Coordinate Geometry
• Chapter 7–Areas
• Chapter 8–Linear Equations in Two Variables
• Chapter 9–Quadrilaterals and Parallelograms
• Chapter 10–Area
• Chapter 11–Circle
• Chapter 12–Geometrical Constructions
• Chapter 13–Volume and Surface Area
• Chapter 14–Statistics
• Chapter 15–Probability

About RS Aggarwal Class 9 Book

Investing in an R.S. Aggarwal book will never be of waste since you can use the book to prepare for various competitive exams as well. RS Aggarwal is one of the most prominent books with an endless number of problems. R.S. Aggarwal’s book very neatly explains every derivation, formula, and question in a very consolidated manner. It has tonnes of examples, practice questions, and solutions even for the NCERT questions.

He was born on January 2, 1946 in a village of Delhi. He graduated from Kirori Mal College, University of Delhi. After completing his M.Sc. in Mathematics in 1969, he joined N.A.S. College, Meerut, as a lecturer. In 1976, he was awarded a fellowship for 3 years and joined the University of Delhi for his Ph.D. Thereafter, he was promoted as a reader in N.A.S. College, Meerut. In 1999, he joined M.M.H. College, Ghaziabad, as a reader and took voluntary retirement in 2003. He has authored more than 75 titles ranging from Nursery to M. Sc. He has also written books for competitive examinations right from the clerical grade to the I.A.S. level.

FAQs

Why must I refer to the RS Aggarwal textbook?
RS Aggarwal is one of the most important reference books for high school grades and is recommended to every high school student. The book covers every single topic in detail. It goes in-depth and covers every single aspect of all the mathematics topics and covers both theory and problem-solving. The book is true of great help for every high school student. Solving a majority of the questions from the book can help a lot in understanding topics in detail and in a manner that is very simple to understand. Hence, as a high school student, you must definitely dwell your hands on RS Aggarwal!

Why should you refer to RS Aggarwal textbook solutions on Indcareer?
RS Aggarwal is a book that contains a few of the hardest questions of high school mathematics. Solving them and teaching students how to solve questions of such high difficulty is not the job of any neophyte. For solving such difficult questions and more importantly, teaching the problem-solving methodology to students, an expert teacher is mandatory!

Does IndCareer cover RS Aggarwal Textbook solutions for Class 6-12?
RS Aggarwal is available for grades 6 to 12 and hence our expert teachers have formulated detailed solutions for all the questions of each edition of the textbook. On our website, you’ll be able to find solutions to the RS Aggarwal textbook right from Class 6 to Class 12. You can head to the website and download these solutions for free. All the solutions are available in PDF format and are free to download!

Read More

• RD Sharma Solutions for Class 9 Maths Chapter 11–Co-ordinate Geometry
• RD Sharma Solutions for Class 9 Maths Chapter 8–Lines and Angles
• RD Sharma Solutions for Class 9 Maths Chapter 9–Triangle and its Angles
• RD Sharma Solutions for Class 9 Maths Chapter 10–Congruent Triangles
• HC Verma Solutions for Class 12 Physics Chapter 27 – Specific Heat Capacities of Gases