RS Aggarwal Solutions for Class 9 Maths Chapter 13–Volume and Surface Area

Class 9: Maths Chapter 13 solutions. Complete Class 9 Maths Chapter 13 Notes.

RS Aggarwal Solutions for Class 9 Maths Chapter 13–Volume and Surface Area

RS Aggarwal 9th Maths Chapter 13, Class 9 Maths Chapter 13 solutions

Ex 13A

Question 1.
Solution:
(i) Length of cuboid (l) = 12cm
Breadth (b) = 8cm
and height (h) = 4.5cm

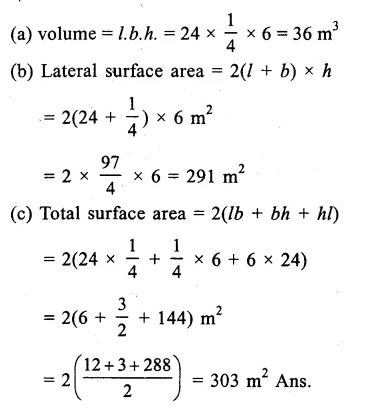
Question 2.
Solution:
Length of closed rectangular cistern (l) = 8m
breadth (b) = 6m
and depth (b) = 2.5m.
(i) .’. Volume of cistern = l.b.h.
= 8 x 6 x 2.5 m³ = 120m³
(ii) Total surface area = 2(lb + bh + hl)
= 2(8 x 6 + 6 x 2.5 + 2.5 x 8) cm²
= 2(48 + 15 + 20)
= 2 x 83 m²
= 166 m² Ans.

Question 3.
Solution:
Length of room (l) = 9m
Breadth (b) = 8m
and height (h) = 6.5m

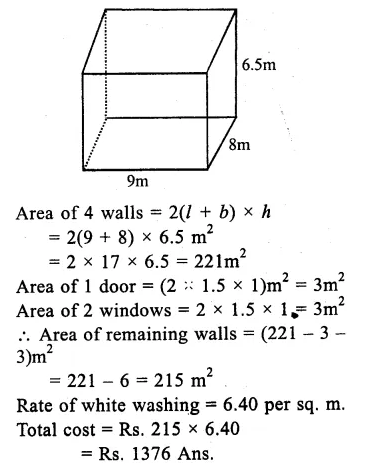
Question 4.
Solution:
Length of pit (l) = 20m
Breadth (b) = 6m

Question 5.
Solution:
Length of wall (l) = 8m.
Width (b) = 22.5 cm = 22510X100=940m
and height (h) = 6m.
Volume of wall = l.b.h.

Question 6.
Solution:
Length of wall (l) = 15m.
Width (b) = 30cm = 30100=310m
Height (h) = 4m

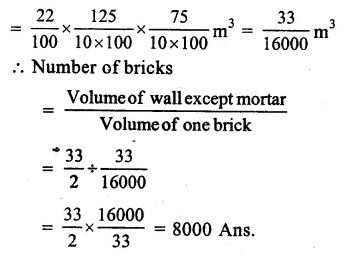
Question 7.
Solution:
Outer length of opened cistern = 1.35m = 135 cm
Breadth = 1.08 m = 108 cm
Depth = 90cm
Thickness of iron = 2.5cm.

Question 8.
Solution:
Depth of river = 2m
width = 45m.
Length of current in 60 minutes = 3km

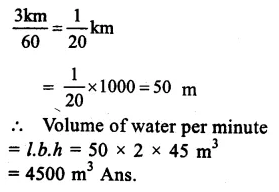
Question 9.
Solution:
Total cost of box = Rs. 1620
Rate per sq. m = Rs. 30

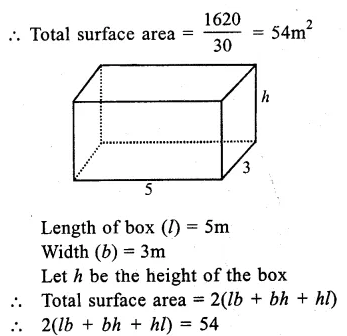
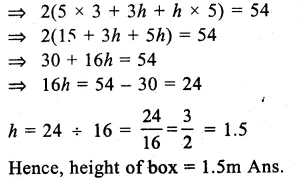
Question 10.
Solution:
Length of room (l) = 10m
Breadth (b) = 10m
Height (h) = 5m

Question 11.
Solution:
Length of hall (l) = 20m
Breadth (b) = 16m
and height (h) = 4.5m.
Volume of the air inside the hall

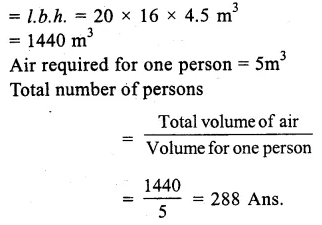
Question 12.
Solution:
Length of class room (l) = 10m
Width (b) = 6.4 m
Height (h) = 5m.

Question 13.
Solution:
Volume of cuboid = 1536 m³
Length (l) = 16m
Ratio in breadth and height = 3:2
Let breadth (b) = 3x
their height (h) = 2x

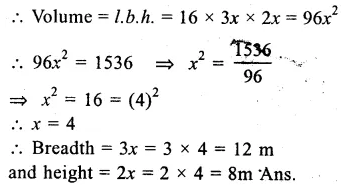
Question 14.
Solution:
Length of cuboid (l) = 14 cm
Breadth (b) = 11 cm .
Let height (h) =x cm
Surface area = 2(lb + bh + hl)

Question 15.
Solution:
(a) Edge of cube (a) = 9m .
(i) volume = a³ = (9)³ m³ = 729 m³
(ii) Lateral surface area = 4a²

Question 16.
Solution:
Total surface area of a cube = 1176 cm²
Let each edge he ‘a’
then 6a² =1176

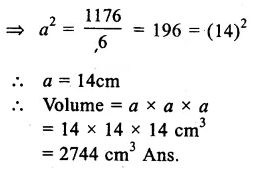
Question 17.
Solution:
Lateral surface area of a cube = 900 cm²
Let ‘a’ be the edge of the cube

Question 18.
Solution:
Volume of a cube = 512 cm³
Let ‘a’ be its edge, then

Question 19.
Solution:
Edge of first-cube = 3 cm.
Volume = (3)³ = 27 cm³

Question 20.
Solution:
Area of ground = 2 hectares
= 2 x 10000 = 20000 m²
Height of rain falls 5cm = 5100m
∴ Volume of rain water = 20000 x 5100 m³
= 1000 m³ Ans.

Ex 13B

Question 1.
Solution:
Radius of the base of a cylinder (r) = 5cm.
and height (h) = 21cm

Question 2.
Solution:
Diameter of the base of the cylinder = 28cm
Radius = 12 x 28 = 14 cm
Height (h) = 40cm.

Question 3.
Solution:
Radius of cylinder (r) = 10.5cm
Height (h) = 60cm.

Question 4.
Solution:
Diameter of cylinder = 20cm
Radius (r) = 202 = 10cm

Question 5.
Solution:
Curved surface area of cylinder = 4400 cm²
Circumference of its base = 110 cm

Question 6.
Solution:
The ratio of the radius and height of a cylinder = 2:3
Volume =1617 cm³
Let radius = 2x
and height = 3x.

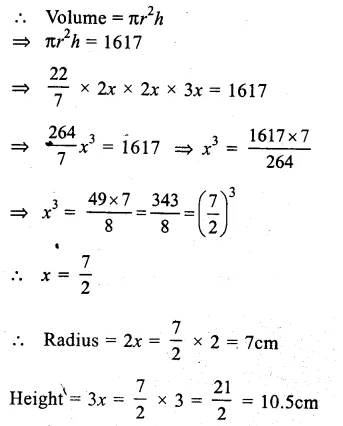
Question 7.
Solution:
Total surface area of the cylinder = 462 cm²
Curved surface area = 13 x 462 = 154

Question 8.
Solution:
Total surface area of solid
cylinder = 231 cm²

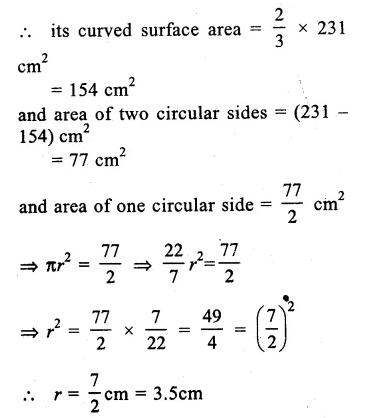
Question 9.
Solution:
Sum of radius and height = 37m.
and total surface area = 1628 m²
Let r be the radius

Question 10.
Solution:
Total surface area = 616 cm²
Curved surface area = 616X12 = 308

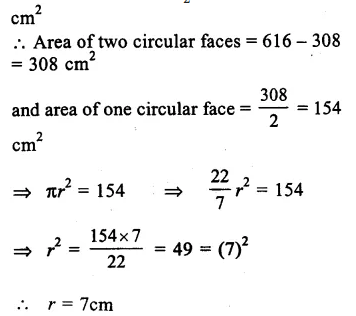
Question 11.
Solution:
Volume of gold = 1 cm³
diameter of wire = 0.1 mn

Question 12.
Solution:
Ratio in the radii of two cylinders = 2:3
and ratio in the heights = 5:3
If r1 and r2 and the radii and h1 and h2 are the heights, then

Question 13.
Solution:
Side of square = 12cm
and height = 17.5cm

Question 14.
Solution:
Diameter of cylindrical bucket = 28cm
Radius (r) = 288 = 14cm
Height (h) = 72cm.

Question 15.
Solution:
Length of pipe (l) = 1m = 100cm
diameter of pipe = 3cm.
Inner radius = 32 cm

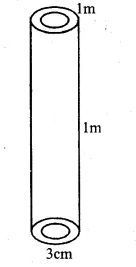
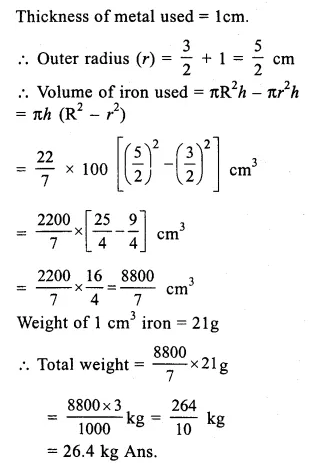
Question 16.
Solution:
Internal diameter of cylindrical tube = 10.4 cm
Radius (r) = 10.42 = 5.2cm.

Question 17.
Solution:
Length of barrel (h) = 7cm
Diameter = 5mm.

Question 18.
Solution:
Diameter of pencil = 7mm
.’. Radius (R) = 72 mm = 720 cm.
and diameter of graphite in it = 1mm

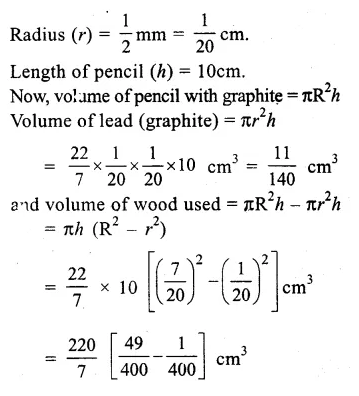
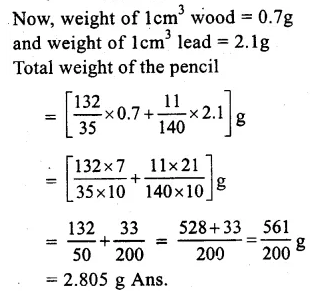
Ex 13C

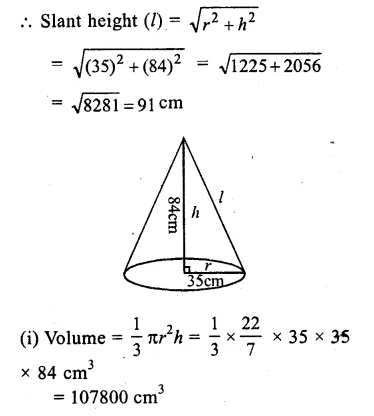
Question 1.
Solution:
Radius of base (r) = 35cm
and height (h) = 84cm.

Question 2.
Solution:
Height of cone (h) = 6cm
Slant height (l) = 10cm.

Question 3.
Solution:
Volume of right circular cone = (100 π) cm³
Height (h) = 12cm.
Let r be the radius of the cone

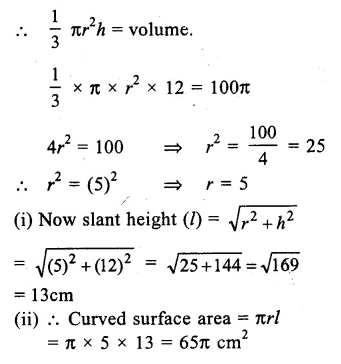
Question 4.
Solution:
Circumference of the base = 44cm

Question 5.
Solution:
Slant height of the cone (l) = 25cm
Curved surface area = 550 cm²
Let r be the radius
πrl = curved surface area

Question 6.
Solution:
Radius.of base (r) = 35cm.
Slant height (l) = 37cm.
We know that

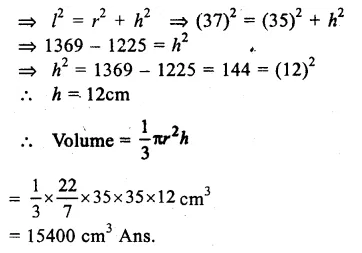
Question 7.
Solution:
Curved surface area = 4070 cm²
Diameter of the base = 70cm

Question 8.
Solution:
Radius of the conical tent = 7m
and height = 24 m.

Question 9.
Solution:
Radius of the first cone (r) = 1.6 cm.
and height (h) = 3.6 cm.

Question 10.
Solution:
Ratio in their heights =1:3
and ratio in their radii = 3:1
Let h1,h2 he their height and r1,r2 be their radii, then

The ratio between their volumes is 3:1
hence proved

Question 11.
Solution:
Diameter of the tent = 105m

Question 12.
Solution:
No. of persons to be s accommodated =11
Area to be required for each person = 4m²

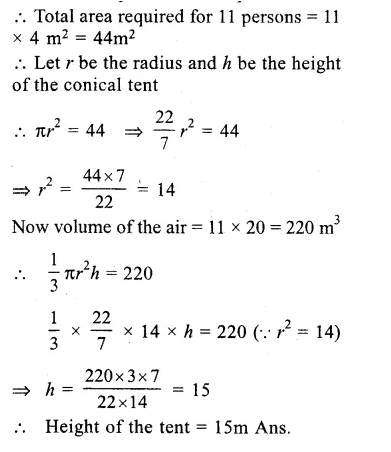
Question 13.
Solution:
Height of the cylindrical bucket (h) = 32cm
Radius (r) = 18cm
Volume of sand filled in it = πr²h
= π x 18 x 18 x 32 cm³
= 10368π cm³
Volume of conical sand = 10368 π cm³
Height of cone = 24 cm

Question 14.
Solution:
Let h be the height and r be the radius of the cylinder and cone.
Curved surface area of cylinder = 2πrh
and curved surface area of cone = πrl

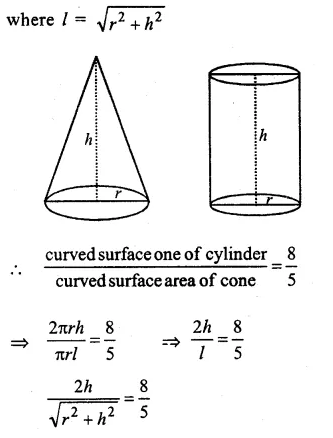
Question 15.
Solution:
Diameter of the pillar = 20cm
Radius (r) = 202 = 10cm

Question 16.
Solution:
Height of the bigger cone (H) = 30cm
By cutting a small cone from it, then volume of smaller cone = 127 of volume of big cone

Let radius and height of the smaller cone be r and h
and radius and height of the bigger cone be R and H.

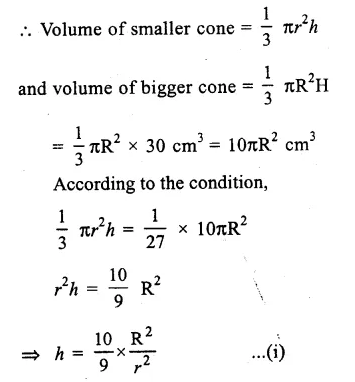
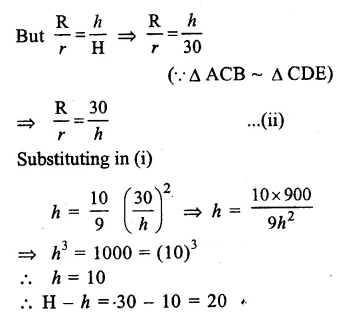
Hence at the height of 20cm from the base it was cut off. Ans.

Question 17.
Solution:
Height of the cylinder (h) = 10cm.
Radius (r) = 6cm.
Height of the cone = 10cm

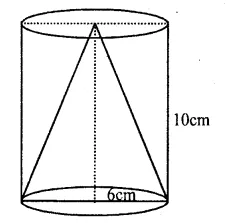
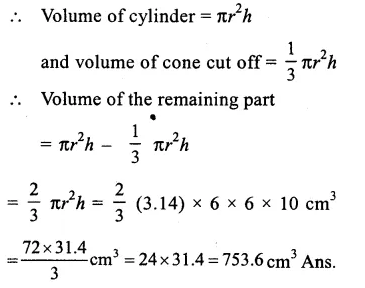
Question 18.
Solution:
Diameter of conical vessel = 40cm
Radius (r) = 402 = 20cm
and depth (h) = 24cm.
.’. Volume = 13 πr²h

Ex 13D

Question 1.
Solution:
(i) Radius of sphere = 3.5cm
(a) Volume = 43 πr³

Question 2.
Solution:
Let r be the radius of the sphere and volume = 38808 cm³
∴43 πr³ = 38803
=> 43 x 227 r³ = 38803

Question 3.
Solution:
Let r be the radius of the sphere
∴ Volume = 43 πr³

Question 4.
Solution:
Surface area of a sphere = 394.24 m²
Let r be the radius, then 4πr² = 394.24

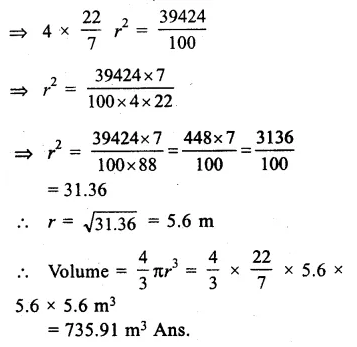
Question 5.
Solution:
Surface area of sphere = 576π cm²
Let r be the radius, then 4r² = 576π

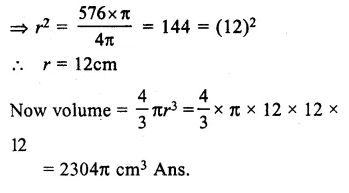
Question 6.
Solution:
Outer diameter of shell = 12cm,
Outer radius (R) = 122 = 6cm
and inner diameter = 8cm

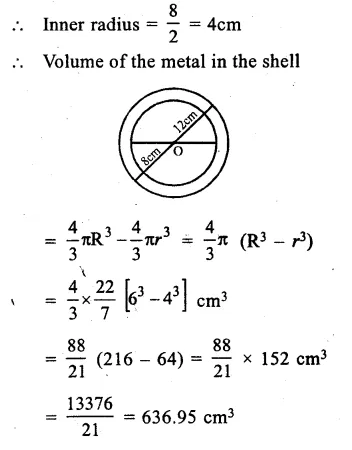
Question 7.
Solution:
Length of cuboid of (l) = 12cm
Breadth (b) = 11cm
and height (h) = 9cm

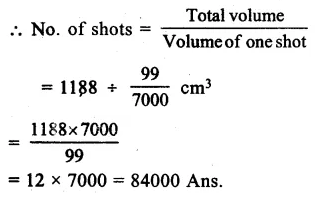
Question 8.
Solution:
Radius of sphere (r) = 8cm
Volume = 43πr³

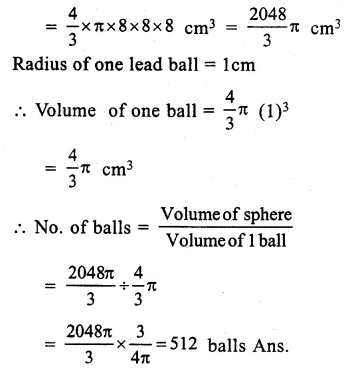
Question 9.
Solution:
Radius of solid sphere (R) = 3cm.
Volume = 43π(R)³ = 43π(3)³ cm³

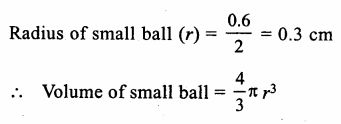
Question 10.
Solution:
Radius of metallic sphere (R) = 10.5cm

Question 11.
Solution:
Diameter of a cylinder = 8cm
Radius (r) = 82 = 4cm

Question 12.
Solution:
Diameter of sphere = 6cm
Radius (R) = 62 = 3cm

Question 13.
Solution:
Diameter of sphere = 18cm
Radius (R) = 182 = 9cm.

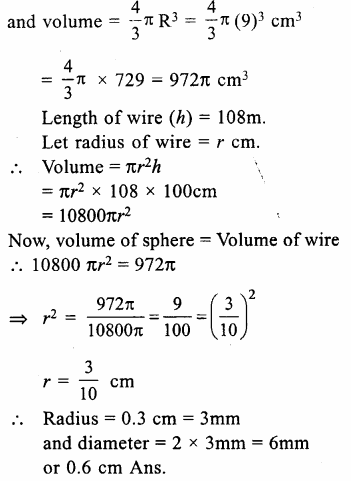
Question 14.
Solution:
Diameter of the sphere = 15.6 cm
Radius (R) = 15.62 = 7.8 cm

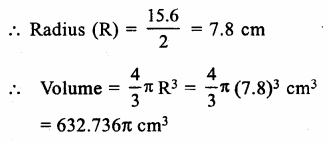
Question 15.
Solution:
Diameter of the canonball = 28cm
Radius (R) = 282 = 14 cm

Question 16.
Solution:
Given,
Radius of spherical big ball (R) = 3cm

Question 17.
Solution:
Ratio in the radii of two spheres = 1:2
Let radius of smaller sphere = r then,
radius of bigger sphere = 2r

Question 18.
Solution:
Let r1 and r2 be the radii of two spheres

Question 19.
Solution:
Radius of the cylindrical tub = 12cm.
First level of water = 20cm
Raised water level = 6.75cm.

Question 20.
Solution:
Radius of the ball (r) = 9cm.
Volume of ball = 43πr³

Question 21.
Solution:
Given,
Radius of hemisphere of lead (r) = 9cm.

Question 22.
Solution:
Given,
Radius of hemispherical bowl (r) = 9cm

Question 23.
Solution:
External radius of spherical shell (R) = 9cm

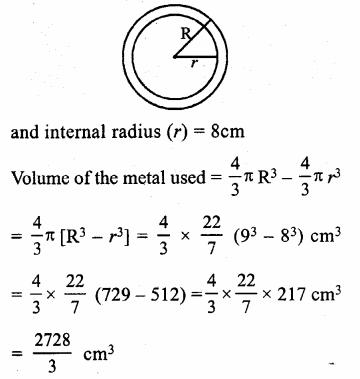
Question 24.
Solution:
Inner radius (r) = 4 cm
Thickness of steel used = 0.5

RS Aggarwal Solutions for Class 9 Maths Chapter 13: Download PDF

RS Aggarwal Solutions for Class 9 Maths Chapter 13–Volume and Surface Area

Download PDF: RS Aggarwal Solutions for Class 9 Maths Chapter 13–Volume and Surface Area PDF

Chapterwise RS Aggarwal Solutions for Class 9 Maths :

• Chapter 1–Real Numbers
• Chapter 2–Polynomials
• Chapter 3–Introduction to Euclid’s Geometry
• Chapter 4–Lines and Triangles
• Chapter 5–Congruence of Triangles and Inequalities in a Triangle
• Chapter 6–Coordinate Geometry
• Chapter 7–Areas
• Chapter 8–Linear Equations in Two Variables
• Chapter 9–Quadrilaterals and Parallelograms
• Chapter 10–Area
• Chapter 11–Circle
• Chapter 12–Geometrical Constructions
• Chapter 13–Volume and Surface Area
• Chapter 14–Statistics
• Chapter 15–Probability

About RS Aggarwal Class 9 Book

Investing in an R.S. Aggarwal book will never be of waste since you can use the book to prepare for various competitive exams as well. RS Aggarwal is one of the most prominent books with an endless number of problems. R.S. Aggarwal’s book very neatly explains every derivation, formula, and question in a very consolidated manner. It has tonnes of examples, practice questions, and solutions even for the NCERT questions.

He was born on January 2, 1946 in a village of Delhi. He graduated from Kirori Mal College, University of Delhi. After completing his M.Sc. in Mathematics in 1969, he joined N.A.S. College, Meerut, as a lecturer. In 1976, he was awarded a fellowship for 3 years and joined the University of Delhi for his Ph.D. Thereafter, he was promoted as a reader in N.A.S. College, Meerut. In 1999, he joined M.M.H. College, Ghaziabad, as a reader and took voluntary retirement in 2003. He has authored more than 75 titles ranging from Nursery to M. Sc. He has also written books for competitive examinations right from the clerical grade to the I.A.S. level.

FAQs

Why must I refer to the RS Aggarwal textbook?
RS Aggarwal is one of the most important reference books for high school grades and is recommended to every high school student. The book covers every single topic in detail. It goes in-depth and covers every single aspect of all the mathematics topics and covers both theory and problem-solving. The book is true of great help for every high school student. Solving a majority of the questions from the book can help a lot in understanding topics in detail and in a manner that is very simple to understand. Hence, as a high school student, you must definitely dwell your hands on RS Aggarwal!

Why should you refer to RS Aggarwal textbook solutions on Indcareer?
RS Aggarwal is a book that contains a few of the hardest questions of high school mathematics. Solving them and teaching students how to solve questions of such high difficulty is not the job of any neophyte. For solving such difficult questions and more importantly, teaching the problem-solving methodology to students, an expert teacher is mandatory!

Does IndCareer cover RS Aggarwal Textbook solutions for Class 6-12?
RS Aggarwal is available for grades 6 to 12 and hence our expert teachers have formulated detailed solutions for all the questions of each edition of the textbook. On our website, you’ll be able to find solutions to the RS Aggarwal textbook right from Class 6 to Class 12. You can head to the website and download these solutions for free. All the solutions are available in PDF format and are free to download!

Read More

• RS Aggarwal Solutions for Class 10 Maths Chapter 17–Volume and Surface Areas of Solids
• RD Sharma Solutions for Class 10 Maths Chapter 16–Surface Areas And Volumes
• NCERT Solutions for 9th class Maths : Chapter 13 Surface Areas and Volumes
• RD Sharma Solutions for Class 8 Maths Chapter 22–Mensuration – III (Surface Area and Volume of a Right Circular Cylinder)
• RD Sharma Solutions for Class 9 Maths Chapter 21–Surface Area And Volume Of Sphere