Class 10: Maths Chapter 10 solutions. Complete Class 10 Maths Chapter 10 Notes.
Contents
- 1 RS Aggarwal Solutions for Class 10 Maths Chapter 10–Trignometric Ratios
- 1.0.1 Page No 546:
- 1.0.2 Question 1:
- 1.0.3 Answer:
- 1.0.4 Page No 546:
- 1.0.5 Question 2:
- 1.0.6 Answer:
- 1.0.7 Page No 546:
- 1.0.8 Question 3:
- 1.0.9 Answer:
- 1.0.10 Page No 546:
- 1.0.11 Question 4:
- 1.0.12 Answer:
- 1.0.13 Page No 546:
- 1.0.14 Question 5:
- 1.0.15 Answer:
- 1.0.16 Page No 546:
- 1.0.17 Question 6:
- 1.0.18 Answer:
- 1.0.19 Page No 546:
- 1.0.20 Question 7:
- 1.0.21 Answer:
- 1.0.22 Page No 546:
- 1.0.23 Question 8:
- 1.0.24 Answer:
- 1.0.25 Page No 546:
- 1.0.26 Question 9:
- 1.0.27 Answer:
- 1.0.28 Page No 546:
- 1.0.29 Question 10:
- 1.0.30 Answer:
- 1.0.31 Page No 547:
- 1.0.32 Question 11:
- 1.0.33 Answer:
- 1.0.34 Page No 547:
- 1.0.35 Question 12:
- 1.0.36 Answer:
- 1.0.37 Page No 547:
- 1.0.38 Question 13:
- 1.0.39 Answer:
- 1.0.40 Page No 547:
- 1.0.41 Question 14:
- 1.0.42 Answer:
- 1.0.43 Page No 547:
- 1.0.44 Question 15:
- 1.0.45 Answer:
- 1.0.46 Page No 547:
- 1.0.47 Question 16:
- 1.0.48 Answer:
- 1.0.49 Page No 547:
- 1.0.50 Question 17:
- 1.0.51 Answer:
- 1.0.52 Page No 547:
- 1.0.53 Question 18:
- 1.0.54 Answer:
- 1.0.55 Page No 547:
- 1.0.56 Question 19:
- 1.0.57 Answer:
- 1.0.58 Page No 547:
- 1.0.59 Question 20:
- 1.0.60 Answer:
- 1.0.61 Page No 547:
- 1.0.62 Question 21:
- 1.0.63 Answer:
- 1.0.64 Page No 547:
- 1.0.65 Question 22:
- 1.0.66 Answer:
- 1.0.67 Page No 547:
- 1.0.68 Question 23:
- 1.0.69 Answer:
- 1.0.70 Page No 547:
- 1.0.71 Question 24:
- 1.0.72 Answer:
- 1.0.73 Page No 548:
- 1.0.74 Question 25:
- 1.0.75 Answer:
- 1.0.76 Page No 548:
- 1.0.77 Question 26:
- 1.0.78 Answer:
- 1.0.79 Page No 548:
- 1.0.80 Question 27:
- 1.0.81 Answer:
- 1.0.82 Page No 548:
- 1.0.83 Question 28:
- 1.0.84 Answer:
- 1.0.85 Page No 548:
- 1.0.86 Question 29:
- 1.0.87 Answer:
- 1.0.88 Page No 548:
- 1.0.89 Question 30:
- 1.0.90 Answer:
- 1.0.91 Page No 555:
- 1.0.92 Question 1:
- 1.0.93 Answer:
- 1.0.94 Page No 555:
- 1.0.95 Question 2:
- 1.0.96 Answer:
- 1.0.97 Page No 555:
- 1.0.98 Question 3:
- 1.0.99 Answer:
- 1.0.100 Page No 555:
- 1.0.101 Question 4:
- 1.0.102 Answer:
- 1.0.103 Page No 555:
- 1.0.104 Question 5:
- 1.0.105 Answer:
- 1.0.106 Page No 555:
- 1.0.107 Question 6:
- 1.0.108 Answer:
- 1.0.109 Page No 556:
- 1.0.110 Question 7:
- 1.0.111 Answer:
- 1.0.112 Page No 556:
- 1.0.113 Question 8:
- 1.0.114 Answer:
- 1.0.115 Page No 556:
- 1.0.116 Question 9:
- 1.0.117 Answer:
- 1.0.118 Page No 556:
- 1.0.119 Question 10:
- 1.0.120 Answer:
- 1.0.121 Page No 556:
- 1.0.122 Question 11:
- 1.0.123 Answer:
- 1.0.124 Page No 556:
- 1.0.125 Question 12:
- 1.0.126 Answer:
- 1.0.127 Page No 556:
- 1.0.128 Question 13:
- 1.0.129 Answer:
- 1.0.130 Page No 556:
- 1.0.131 Question 14:
- 1.0.132 Answer:
- 1.0.133 Page No 556:
- 1.0.134 Question 15:
- 1.0.135 Answer:
- 1.0.136 Page No 556:
- 1.0.137 Question 16:
- 1.0.138 Answer:
- 2 RS Aggarwal Solutions for Class 10 Maths Chapter 10: Download PDF
- 3 About Rs Aggarwal
- 4 Read More
RS Aggarwal Solutions for Class 10 Maths Chapter 10–Trignometric Ratios
RS Aggarwal 10th Maths Chapter 1, Class 10 Maths Chapter 10 solutions
Page No 546:
Question 1:
If sin , find the value of all T-ratios of θ.
Answer:
Let us first draw a right ABC, right angled at B and .
Now, we know that sin = = = .

So, if AB = , then AC = 2k, where k is a positive number.
Now, using Pythagoras theorem, we have:
AC2 = AB2 + BC2
⇒ BC2 = AC2 AB2 = (2k)2 ()2
⇒ BC2 = 4k2 3k2 = k2
⇒ BC = k
Now, finding the other T-ratios using their definitions, we get:
cos = =
tan =
∴ cot = , cosec = and sec =
Page No 546:
Question 2:
If cos find the values of all T-ratios of θ.
Answer:
Let us first draw a right ABC, right angled at B and .
Now, we know that cos = = = .
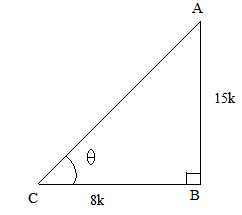
So, if BC = 7k, then AC = 25k, where k is a positive number.
Now, using Pythagoras theorem, we have:
AC2 = AB2 + BC2
⇒ AB2 = AC2 BC2 = (25k)2 (7k)2.
⇒ AB2 = 625k2 49k2 = 576k2
⇒ AB = 24k
Now, finding the other trigonometric ratios using their definitions, we get:
sin = =
tan =
∴ cot = , cosec = and sec =
Page No 546:
Question 3:
If tan find the values of all T-ratios of θ.
Answer:
Let us first draw a right ABC, right angled at B and .
Now, we know that tan = = = .
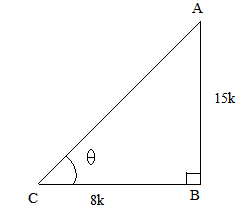
So, if BC = 8k, then AB = 15k, where k is a positive number.
Now, using Pythagoras theorem, we have:
AC2 = AB2 + BC2 = (15k)2 + (8k)2
⇒ AC2 = 225k2 + 64k2 = 289k2
⇒ AC = 17k
Now, finding the other T-ratios using their definitions, we get:
sin = =
cos =
∴ cot = , cosec = and sec =
Page No 546:
Question 4:
If cot θ = 2, find the value of all T-ratios of θ.
Answer:
Let us first draw a right ABC, right angled at B and .
Now, we know that cot = = = 2.

So, if BC = 2k, then AB = k, where k is a positive number.
Now, using Pythagoras theorem, we have:
AC2 = AB2 + BC2 = (2k)2 + (k)2
⇒ AC2 = 4k2 + k2 = 5k2
⇒ AC = k
Now, finding the other T-ratios using their definitions, we get:
sin = =
cos =
∴ tan = , cosec = and sec =
Page No 546:
Question 5:
If cosec θ = , the find the values of all T-ratios of θ.
Answer:
Let us first draw a right ABC, right angled at B and .
Now, we know that cosec = = = .
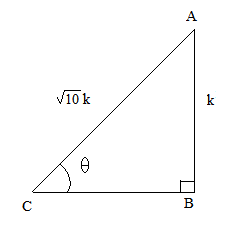
So, if AC = ()k, then AB = k, where k is a positive number.
Now, by using Pythagoras theorem, we have:
AC2 = AB2 + BC2
⇒ BC2 = AC2 AB2 = 10k2 k2
⇒ BC2 = 9k2
⇒ BC = 3k
Now, finding the other T-ratios using their definitions, we get:
tan = =
cos =
∴ , cot = and sec =
Page No 546:
Question 6:
If , find the values of all T-ratios of .
Answer:
We have ,
As,
Also,
Now,
Also,
And,
Page No 546:
Question 7:
If , where d > 0 then find the values of cos θ and tan θ.
Answer:
Page No 546:
Question 8:
If then evaluate (cos2θ – sin2θ).
Answer:
Page No 546:
Question 9:
If 4tan θ = 3 then prove that .
Answer:
Page No 546:
Question 10:
If , show that .
Answer:
Page No 547:
Question 11:
If tan θ = ab, show that (a sinθ−b cosθa sinθ+b cosθ)=(a2−b2)(a2+b2).
Answer:
It is given that tan θ = ab.
LHS = a sinθ − b cosθa sinθ + b cosθ
Dividing the numerator and denominator by cos θ, we get:
a tan θ − ba tan θ + b (∵ tan θ = sin θcos θ)
Now, substituting the value of tan θ in the above expression, we get:
a(ab) − ba(ab) + b= a2b − ba2b + b= a2 − b2a2 + b2 = RHS
i.e., LHS = RHS
Hence proved.
Page No 547:
Question 12:
If sin θ=1213 then evaluate (2sin θ−3cos θ4sin θ−9cos θ).
Answer:
Given: sinθ=1213Since, sinθ=PH⇒P=12 and H=13Using Pythagoras theorem,P2+B2=H2⇒122+B2=132⇒B2=169−144⇒B2=25⇒B=5Therefore,cosθ=BH=513Now,(2sinθ−3cosθ4sinθ−9cosθ)=(2(1213)−3(513)4(1213)−9(513)) =(2413−15134813−4513) =(24−1548−45) =93 =3Hence, (2sinθ−3cosθ4sinθ−9cosθ)=3.
Page No 547:
Question 13:
If tan θ=12 then evaluate (cos θsin θ+sin θ1+cos θ)
Answer:
Given: tanθ=12Since, tanθ=PB⇒P=1 and B=2Using Pythagoras theorem,P2+B2=H2⇒12+22=H2⇒H2=1+4⇒H2=5⇒H=5–√Therefore,sinθ=PH=15√cosθ=BH=25√Now,(cosθsinθ+sinθ1+cosθ)=(25√15√+15√1+25√) =⎛⎝21+15√5√+25√⎞⎠ =(21+15√+2) =(2+(15√+2×5√−25√−2)) =(2+(5√−25−4)) =(2+5–√−2) =5–√Hence, (cosθsinθ+sinθ1+cosθ)=5–√.
Page No 547:
Question 14:
If sinα=12, prove that (3cosα−4cos3α)=0.
Answer:
LHS=(3cosα−4cos3α)=cosα(3−4cos2α)=1−sin2α−−−−−−−−√[3−4(1−sin2α)]=1−(12)2−−−−−−−√[3−4(1−(12)2)]=11−14−−−−−√[3−4(11−14)]=34−−√[3−4(34)]=34−−√[3−3]=34−−√[0]=0=RHS
Page No 547:
Question 15:
If 3 cot θ = 2, show that (4sinθ−3cosθ2sinθ+6cosθ)=13.
Answer:
It is given that cot θ = 23.
LHS = 4 sinθ − 3 cosθ2 sinθ + 6 cosθ
Dividing the above expression by sin θ, we get:
4 − 3 cot θ2 + 6 cot θ [∵ cot θ = cosθsinθ]
Now, substituting the values of cot θ in the above expression, we get:
4 − 3(23)2 + 6(23)= 4 − 22 + 4 = 26=13
i.e., LHS = RHS
Hence proved.
Page No 547:
Question 16:
If sec θ = 178 then prove that 3−4sin2θ4cos2θ−3=3−tan2θ1−3tan2θ.
Answer:
It is given that sec θ = 178.
Let us consider a right △ABC right angled at B and ∠C=θ.
We know that cos θ = 1sec θ= 817 = BCAC

So, if BC = 8k, then AC = 17k, where k is a positive number.
Using Pythagoras theorem, we have:
AC2 = AB2 + BC2
⇒ AB2 = AC2 − BC2 = (17k)2 − (8k)2
⇒ AB2 = 289k2 − 64k2 = 225k2
⇒ AB = 15k.
Now, tan θ = ABBC = 158 and sin θ = ABAC = 15k17k= 1517
The given expression is 3 − 4sin2θ4cos2θ− 3 = 3 − tan2θ1 − 3tan2θ.
Substituting the values in the above expression, we get:
LHS= 3 − 4(1517)24(817)2 − 3 = 3 − 900289256289− 3 = 867−900256−867= −33−611=33611
RHS = 3−(158)21−3(158)2=3−225641−67564=192−22564−675=−33−611=33611
∴ LHS = RHS
Hence proved.
Page No 547:
Question 17:
If tan θ = 2021, show that(1−sinθ+cosθ)(1+sinθ+cosθ)=37.
Answer:
Let us consider a right △ABC right angled at B and ∠C=θ.
Now, we know that tan θ = ABBC = 2021

So, if AB = 20k, then BC = 21k, where k is a positive number.
Using Pythagoras theorem, we get:
AC2 = AB2 + BC2
⇒ AC2= (20k)2 + (21k)2
⇒ AC2 = 841k2
⇒ AC = 29k
Now, sin θ = ABAC = 2029 and cos θ = BCAC = 2129
Substituting these values in the given expression, we get:
LHS=1 − sinθ + cosθ1 + sinθ + cosθ= 1 − 2029 + 21291 + 2029 + 2129= 29 − 20 + 212929 + 20 + 2129= 3070 = 37 = RHS
∴ LHS = RHS
Hence proved.
Page No 547:
Question 18:
If tan θ = 17√ then prove that (cosec2θ+sec2θcosec2θ−sec2θ)=43.
Answer:
Let us consider a right △△ABC, right-angled at B and .
Now it is given that tan = = .

So, if AB = k, then BC = k, where k is a positive number.
Using Pythagoras theorem, we have:
AC2 = AB2 + BC2
⇒ AC2 = (k)2 + (k)2
⇒ AC2 = k2 + 7k2
⇒ AC = 2k
Now, finding out the values of the other trigonometric ratios, we have:
sin =
cos =
∴ cosec = and sec =
Substituting the values of cosec and sec in the given expression, we get:
i.e., LHS = RHS
Hence proved.
Page No 547:
Question 19:
If sinθ=34, show that cosec2θ−cot2θsec2θ−1−−−−−−−−−√=7√3.
Answer:
LHS=cosec2θ−cot2θsec2θ−1−−−−−−−−−√=1tan2θ−−−−√=cot2θ−−−−−√=cotθ=cosec2θ−1−−−−−−−−−√=(1sinθ)2−1−−−−−−−−−√=(1(34))2−1−−−−−−−−−−⎷=(43)2−1−−−−−−−√=169−1−−−−−√=16−99−−−−√=79−−√=7√3=RHS
Page No 547:
Question 20:
If 3 tan A = 4 then prove that
(i) sec A−cosec Asec A+cosec A−−−−−−−−−−√=17√
(ii) 1−sin A1+cos A−−−−−−√=122√
Answer:
(i)
LHS=secθ−cosecθsecθ+cosecθ−−−−−−−−√=(1cosθ−1sinθ)(1cosθ+1sinθ)−−−−−−−−−⎷=(sinθ−cosθsinθ cosθ)(sinθ+cosθsinθ cosθ)−−−−−−−−⎷=(sinθ−cosθsinθ)(sinθ+cosθsinθ)−−−−−−−−⎷=(sinθsinθ−cosθsinθ)(sinθsinθ+cosθsinθ)−−−−−−−−−⎷=1−cotθ1+cotθ−−−−−√=(1−34)(1+34)−−−−−⎷
=(14)(74)−−−−⎷=17−−√=17√=RHS
(ii)
Given: 3tanA=4⇒tanA=43Since, tanA=PB⇒P=4 and B=3Using Pythagoras theorem,P2+B2=H2⇒42+32=H2⇒H2=16+9⇒H2=25⇒H=5Therefore,sinA=PH=45cosA=BH=35Now,1−sinA1+cosA−−−−−−√=1−451+35−−−−⎷ =5−455+35−−−⎷ =1585−−⎷ =18−−√ =122√Hence, 1−sinA1+cosA−−−−−−√=122√.
Page No 547:
Question 21:
If cot θ=158 then evaluate (1+sin θ) (1−sin θ)(1+cos θ) (1−cos θ).
Answer:
Given: cotθ=158Since, cotθ=BP⇒P=8 and B=15Using Pythagoras theorem,P2+B2=H2⇒82+152=H2⇒H2=64+225⇒H2=289⇒H=17Therefore,sinθ=PH=817cosθ=BH=1517Now,(1+sinθ)(1−sinθ)(1+cosθ)(1−cosθ)=1−sin2θ1−cos2θ =cos2θsin2θ (∵sin2θ+cos2θ=1) =cot2θ =(158)2 =22564Hence, (1+sinθ)(1−sinθ)(1+cosθ)(1−cosθ)=22564.
Page No 547:
Question 22:
In a right ΔABC, right-angled at B, if tanA=1, then verify that 2sinA⋅cosA=1.
Answer:
We have,tanA=1⇒sinAcosA=1⇒sinA=cosA⇒sinA−cosA=0Squaring both sides, we get(sinA−cosA)2=0⇒sin2A+cos2A−2sinA⋅cosA=0⇒1−2sinA⋅cosA=0∴2sinA⋅cosA=1
Page No 547:
Question 23:
In the given figure, ABCD is a rectangle in which diag. AC = 17 cm, ∠BCA = θ and sin θ=817.
Find (i) the area of rect. ABCD, (ii) the perimeter of rect. ABCD.
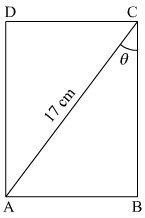
Answer:
Given: In ΔABC,AC=17 cmsinθ=817Since, sinθ=PH⇒P=8 and H=17Using Pythagoras theorem,P2+B2=H2⇒82+B2=172⇒B2=289−64⇒B2=225⇒B=15Therefore,AB= 8 cm and BC=15 cmTherefore,(i) Area of rectangle ABCD=AB×BC =8×15 =120 cm2(ii) Perimeter of rectangle ABCD=2(AB+BC) =2(8+15) =2(23) =46 cm
Page No 547:
Question 24:
If x=cosecA+cosA and y=cosecA−cosA, then prove that (2x+y)2+(x−y2)2−1=0.
Answer:
LHS=(2x+y)2+(x−y2)2−1=[2(cosecA+cosA)+(cosecA−cosA)]2+[(cosecA+cosA)−(cosecA−cosA)2]2−1=[2cosecA+cosA+cosecA−cosA]2+[cosecA+cosA−cosecA+cosA2]2−1=[22cosecA]2+[2cosA2]2−1
=[1cosecA]2+[cosA]2−1=[sinA]2+[cosA]2−1=sin2A+cos2A−1=1−1=0=RHS
Page No 548:
Question 25:
If x=cotA+cosA and y=cotA−cosA, prove that (x−yx+y)2+(x−y2)2=1.
Answer:
LHS=(x−yx+y)2+(x−y2)2=[(cotA+cosA)−(cotA−cosA)(cotA+cosA)+(cotA−cosA)]2+[(cotA+cosA)−(cotA−cosA)2]2=[cotA+cosA−cotA+cosAcotA+cosA+cotA−cosA]2+[cotA+cosA−cotA+cosA2]2=[2cosA2cotA]2+[2cosA2]2=[cosA(cosAsinA)]2+[cosA]2=[sinA cosAcosA]2+[cosA]2=[sinA]2+[cosA]2=sin2A+cos2A=1=RHS
Page No 548:
Question 26:
In the figure of ΔPQR, ∠P=θ° and ∠R=ϕ°. Find
(i) (x+1−−−−−√)cotϕ(ii) (x3+x2−−−−−−√)tanθ(iii) cosθ
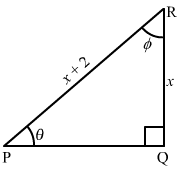
Answer:

In ΔPQR, ∠Q=90°,
Using Pythagoras theorem, we get
PQ=PR2−QR2−−−−−−−−−√=(x+2)2−x2−−−−−−−−−−−√=x2+4x+4−x2−−−−−−−−−−−−−√=4(x+1)−−−−−−−√=2x+1−−−−−√
Now,
(i) (x+1−−−−−√)cotϕ=(x+1−−−−−√)×QRPQ=(x+1−−−−−√)×x2x+1√=x2
(ii) (x3+x2−−−−−−√)tanθ=(x2(x+1)−−−−−−−−√)×QRPQ=x(x+1)−−−−−−√×x2x+1√=x22
(iii) cosθ=PQPR=2x+1√(x+2)
Page No 548:
Question 27:
If cot A+1cot A=2, find the value of (cot2A+1cot2A).
Answer:
Given: cotA+1cotA=2cotA+1cotA=2Squaring both sides, we get⇒(cotA+1cotA)2=22⇒cot2A+(1cotA)2+2(cotA)(1cotA)=4⇒cot2A+1cot2A+2=4⇒cot2A+1cot2A=4−2⇒cot2A+1cot2A=2Hence, the value of (cot2A+1cot2A) is 2.
Page No 548:
Question 28:
Answer:
Page No 548:
Question 29:
If A and B are acute angles such that sinA = sinB, then prove that A = B.
Answer:
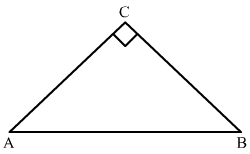
In ABC, C = 90
sinA = and
sinB =
As, sinA = sinB
=
BC = AC
So, A = B (Angles opposite to equal sides are equal)
Page No 548:
Question 30:
If and are acute angles such that tanA = tanB, the prove that .
Answer:
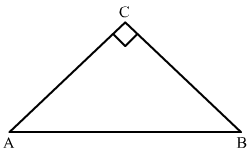
In ,
Page No 555:
Question 1:
If
(a)
(b)
(c)
(d)
Answer:
Hence, the correct option is (c).
Page No 555:
Question 2:
If = ?
(a) 2
(b)
(c)
(d)
Answer:
Hence, the correct option is (a).
Page No 555:
Question 3:
If
(a)
(b)
(c)
(d)
Answer:
Hence, the correct option is (d).
Page No 555:
Question 4:
If
(a)
(b)
(c)
(d)
Answer:
Hence, the correct option is (b).
Page No 555:
Question 5:
If
(a)
(b) 1
(c)
(d)
Answer:
Hence, the correct option is (c).
Page No 555:
Question 6:
If
(a)
(b)
(c)
(d)
Answer:
Hence, the correct option is (a).
Page No 556:
Question 7:
If
(a)
(b)
(c)
(d)
Answer:
Hence, the correct option is (c).
Page No 556:
Question 8:
If (tan θ + cot θ) = 5 then (tan2 θ + cot2 θ) = ?
(a) 27
(b) 25
(c) 24
(d) 23
Answer:
Page No 556:
Question 9:
If (cos θ + sec θ) = then (cos2 θ + sec2 θ) = ?
(a)
(b)
(c)
(d)
Answer:
Page No 556:
Question 10:
If 4tan θ = 3 then (cos2 θ – sin2 θ) = ?
(a)
(b)
(c) 1
(d)
Answer:
Page No 556:
Question 11:
If
(a)
(b)
(c)
(d) 0
Answer:
Page No 556:
Question 12:
If 3cos θ = 2 then (2sec2 θ + 2tan2 θ – 7) = ?
(a) 0
(b) 1
(c) 3
(4) 4
Answer:
Page No 556:
Question 13:
If sec θ + tan θ + 1 = 0 then (sec θ – tan θ) = ?
(a) 1
(b) –1
(c) 0
(d) 2
Answer:
Page No 556:
Question 14:
If cos A + cos2 A = 1 then (sin2 A + sin4 A) = ?
(a)
(b) 2
(c) 1
(d) 4
Answer:
Page No 556:
Question 15:
If
(a)
(b)
(c)
(d)
Answer:
Page No 556:
Question 16:
If tan θ = 3sin θ then (sin2θ – cos2θ) = ?
(a)
(b)
(c)
(d)
Answer:
Hence, the correct option is (a).
RS Aggarwal Solutions for Class 10 Maths Chapter 10: Download PDF
RS Aggarwal Solutions for Class 10 Maths Chapter 10–Trignometric Ratios
Download PDF: RS Aggarwal Solutions for Class 10 Maths Chapter 10–Trignometric Ratios PDF
About Rs Aggarwal
He was born on January 2, 1946 in a village of Delhi. He graduated from Kirori Mal College, University of Delhi. After completing his M.Sc. in Mathematics in 1969, he joined N.A.S. College, Meerut, as a lecturer. In 1976, he was awarded a fellowship for 3 years and joined the University of Delhi for his Ph.D. Thereafter, he was promoted as a reader in N.A.S. College, Meerut. In 1999, he joined M.M.H. College, Ghaziabad, as a reader and took voluntary retirement in 2003. He has authored more than 75 titles ranging from Nursery to M. Sc. He has also written books for competitive examinations right from the clerical grade to the I.A.S. level.
