RD Sharma Solutions for Class 8 Maths Chapter 8–Division of Algebraic Expressions
RD Sharma Solutions for Class 8 Maths Chapter 8–Division of Algebraic Expressions

Class 8: Maths Chapter 8 solutions. Complete Class 8 Maths Chapter 8 Notes.

RD Sharma Solutions for Class 8 Maths Chapter 8–Division of Algebraic Expressions

RD Sharma 8th Maths Chapter 8, Class 8 Maths Chapter 8 solutions

EXERCISE 8.1 PAGE NO: 8.2

1. Write the degree of each of the following polynomials:

(i) 2x3 + 5x2 – 7

(ii) 5x2 – 3x + 2

(iii) 2x + x2 – 8

(iv) 1/2y7 – 12y6 + 48y5 – 10

(v) 3x3 + 1

(vi) 5

(vii) 20x3 + 12x2y2 – 10y2 + 20

Solution:

(i) 2x3 + 5x2 – 7

We know that in a polynomial, degree is the highest power of the variable.

The degree of the polynomial, 2x3 + 5x2 – 7 is 3.

(ii) 5x2 – 3x + 2

The degree of the polynomial, 5x2 – 3x + 2 is 2.

(iii) 2x + x2 – 8

The degree of the polynomial, 2x + x2 – 8 is 2.

(iv) 1/2y7 – 12y6 + 48y5 – 10

The degree of the polynomial, 1/2y7 – 12y6 + 48y5 – 10 is 7.

(v) 3x3 + 1

The degree of the polynomial, 3x3 + 1 is 3

(vi) 5

The degree of the polynomial, 5 is 0 (since 5 is a constant number).

(vii) 20x3 + 12x2y2 – 10y2 + 20

The degree of the polynomial, 20x3 + 12x2y2 – 10y2 + 20 is 4.

2. Which of the following expressions are not polynomials?

(i) x2 + 2x-2

(ii) √(ax) + x2 – x3

(iii) 3y3 – √5y + 9

(iv) ax1/2 + ax + 9x2 + 4

(v) 3x-3 + 2x-1 + 4x + 5

Solution:

(i) x2 + 2x-2

The given expression is not a polynomial.

Because a polynomial does not contain any negative powers or fractions.

(ii) √(ax) + x2 – x3

The given expression is a polynomial.

Because the polynomial has positive powers.

(iii) 3y3 – √5y + 9

The given expression is a polynomial.

Because the polynomial has positive powers.

(iv) ax1/2 + ax + 9x2 + 4

The given expression is not a polynomial.

Because a polynomial does not contain any negative powers or fractions.

(v) 3x-3 + 2x-1 + 4x + 5

The given expression is not a polynomial.

Because a polynomial does not contain any negative powers or fractions.

3. Write each of the following polynomials in the standard from. Also, write their degree:

(i) x2 + 3 + 6x + 5x4

(ii) a2 + 4 + 5a6

(iii) (x3 – 1) (x3 – 4)

(iv) (y3 – 2) (y3 + 11)

(v) (a3 – 3/8) (a3 + 16/17)

(vi) (a + 3/4) (a + 4/3)

Solution:

(i) x2 + 3 + 6x + 5x4

The standard form of the polynomial is written in either increasing or decreasing order of their powers.

3 + 6x + x2 + 5x4 or 5x4 + x2 + 6x + 3

The degree of the given polynomial is 4.

(ii) a2 + 4 + 5a6

The standard form of the polynomial is written in either increasing or decreasing order of their powers.

4 + a2 + 5a6 or 5a6 + a2 + 4

The degree of the given polynomial is 6.

(iii) (x3 – 1) (x3 – 4)

x6 – 4x3 – x3 + 4

x6 – 5x3 + 4

The standard form of the polynomial is written in either increasing or decreasing order of their powers.

x6 – 5x3 + 4 or 4 – 5x3 + x6

The degree of the given polynomial is 6.

(iv) (y3 – 2) (y3 + 11)

y6 + 11y3 – 2y3 – 22

y6 + 9y3 – 22

The standard form of the polynomial is written in either increasing or decreasing order of their powers.

y6 + 9y3 – 22 or -22 + 9y3 + y6

The degree of the given polynomial is 6.

(v) (a3 – 3/8) (a3 + 16/17)

a6 + 16a3/17 – 3a3/8 – 6/17

a6 + 77/136a3 – 48/136

The standard form of the polynomial is written in either increasing or decreasing order of their powers.

a6 + 77/136a3 – 48/136 or -48/136 + 77/136a3 + a6

The degree of the given polynomial is 6.

(vi) (a + 3/4) (a + 4/3)

a2 + 4a/3 + 3a/4 + 1

a2 + 25a/12 + 1

The standard form of the polynomial is written in either increasing or decreasing order of their powers.

a2 + 25a/12 + 1 or 1 + 25a/12 + a2

The degree of the given polynomial is 2.

EXERCISE 8.2 PAGE NO: 8.4

Divide:

1. 6x3y2z2 by 3x2yz

Solution:

We have,

6x3y2z2 / 3x2yz

By using the formula an / am = an-m

6/3 x3-2 y2-1 z2-1

2xyz

2. 15m2n3 by 5m2n2

Solution:

We have,

15m2n3 / 5m2n2

By using the formula an / am = an-m

15/5 m2-2 n3-2

3n

3. 24a3b3 by -8ab

Solution:

We have,

24a3b3 / -8ab

By using the formula an / am = an-m

24/-8 a3-1 b3-1

-3a2b2

4. -21abc2 by 7abc

Solution:

We have,

-21abc2 / 7abc

By using the formula an / am = an-m

-21/7 a1-1 b1-1 c2-1

-3c

5. 72xyz2 by -9xz

Solution:

We have,

72xyz2 / -9xz

By using the formula an / am = an-m

72/-9 x1-1 y z2-1

-8yz

6. -72a4b5c8 by -9a2b2c3

Solution:

We have,

-72a4b5c8 / -9a2b2c3

By using the formula an / am = an-m

-72/-9 a4-2 b5-2 c8-3

8a2b3c5

Simplify:

7. 16m3y2 / 4m2y

Solution:

We have,

16m3y2 / 4m2y

By using the formula an / am = an-m

16/4 m3-2 y2-1

4my

8. 32m2n3p2 / 4mnp

Solution:

We have,

32m2n3p2 / 4mnp

By using the formula an / am = an-m

32/4 m2-1 n3-1 p2-1

8mn2p

EXERCISE 8.3 PAGE NO: 8.6

Divide:

1. x + 2x2 + 3x4 – x5 by 2x

Solution:

We have,

(x + 2x2 + 3x4 – x5) / 2x

x/2x + 2x2/2x + 3x4/2x – x5/2x

By using the formula an / am = an-m

1/2 x1-1 + x2-1 + 3/2 x4-1 – 1/2 x5-1

1/2 + x + 3/2 x3 – 1/2 x4

2. y4 – 3y3 + 1/2y2 by 3y

Solution:

We have,

(y4 – 3y3 + 1/2y2)/ 3y

y4/3y – 3y3/3y + (½)y2/3y

By using the formula an / am = an-m

1/3 y4-1 – y3-1 + 1/6 y2-1

1/3y3 – y2 + 1/6y

3. -4a3 + 4a2 + a by 2a

Solution:

We have,

(-4a3 + 4a2 + a) / 2a

-4a3/2a + 4a2/2a + a/2a

By using the formula an / am = an-m

-2a3-1 + 2a2-1 + 1/2 a1-1

-2a2 + 2a + ½

4. –x6 + 2x4 + 4x3 + 2x2 by √2x2

Solution:

We have,

(–x6 + 2x4 + 4x3 + 2x2) / √2x2

-x6/√2x2 + 2x4/√2x2 + 4x3/√2x2 + 2x2/√2x2

By using the formula an / am = an-m

-1/√2 x6-2 + 2/√2 x4-2 + 4/√2 x3-2 + 2/√2 x2-2

-1/√2 x4 + √2x2 + 2√2x + √2

5. -4a3 + 4a2 + a by 2a

Solution:

We have,

(-4a3 + 4a2 + a) / 2a

-4a3/2a + 4a2/2a + a/2a

By using the formula an / am = an-m

-2a3-1 + 2a2-1 + 1/2a1-1

-2a2 + 2a + ½

6. √3a4 + 2√3a3 + 3a2 – 6a by 3a

Solution:

We have,

(√3a4 + 2√3a3 + 3a2 – 6a) / 3a

√3a4/3a + 2√3a3/3a + 3a2/3a – 6a/3a

By using the formula an / am = an-m

√3/3 a4-1 + 2√3/3 a3-1 + a2-1 – 2a1-1

1/√3 a3 + 2/√3 a2 + a – 2

EXERCISE 8.4 PAGE NO: 8.11

Divide:

1. 5x3 – 15x2 + 25x by 5x

Solution:

We have,

(5x3 – 15x2 + 25x) / 5x

5x3/5x – 15x2/5x + 25x/5x

By using the formula an / am = an-m

5/5 x3-1 – 15/5 x2-1 + 25/5 x1-1

x2 – 3x + 5

2. 4z3 + 6z2 – z by -1/2z

Solution:

We have,

(4z3 + 6z2 – z) / -1/2z

4z3/(-1/2z) + 6z2/(-1/2z) – z/(-1/2z)

By using the formula an / am = an-m

-8 z3-1 – 12z2-1 + 2 z1-1

-8z2 – 12z + 2

3. 9x2y – 6xy + 12xy2 by -3/2xy

Solution:

We have,

(9x2y – 6xy + 12xy2) / -3/2xy

9x2y/(-3/2xy) – 6xy/(-3/2xy) + 12xy2/(-3/2xy)

By using the formula an / am = an-m

(-9×2)/3 x2-1y1-1 – (-6×2)/3 x1-1y1-1 + (-12×2)/3 x1-1y2-1

-6x + 4 – 8y

4. 3x3y2 + 2x2y + 15xy by 3xy

Solution:

We have,

(3x3y2 + 2x2y + 15xy) / 3xy

3x3y2/3xy + 2x2y/3xy + 15xy/3xy

By using the formula an / am = an-m

3/3 x3-1y2-1 + 2/3 x2-1y1-1 + 15/3 x1-1y1-1

x2y + 2/3x + 5

5. x2 + 7x + 12 by x + 4

Solution:

We have,

(x2 + 7x + 12) / (x + 4)

By using long division method

∴ (x2 + 7x + 12) / (x + 4) = x + 3

6. 4y2 + 3y + 1/2 by 2y + 1

Solution:

We have,

4y2 + 3y + 1/2 by (2y + 1)

By using long division method

∴ (4y2 + 3y + 1/2) / (2y + 1) = 2y + 1/2

7. 3x3 + 4x2 + 5x + 18 by x + 2

Solution:

We have,

(3x3 + 4x2 + 5x + 18) / (x + 2)

By using long division method

∴ (3x3 + 4x2 + 5x + 18) / (x + 2) = 3x2 – 2x + 9

8. 14x2 – 53x + 45 by 7x – 9

Solution:

We have,

(14x2 – 53x + 45) / (7x – 9)

By using long division method

∴ (14x2 – 53x + 45) / (7x – 9) = 2x – 5

9. -21 + 71x – 31x2 – 24x3 by 3 – 8x

Solution:

We have,

-21 + 71x – 31x2 – 24x3 by 3 – 8x

(-24x3 – 31x2 + 71x – 21) / (3 – 8x)

By using long division method

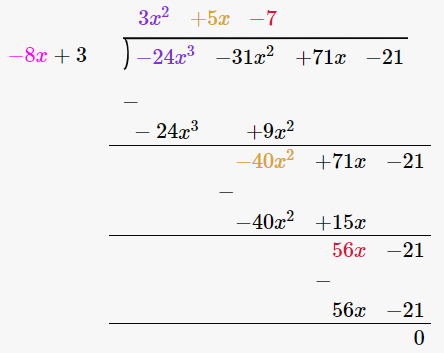
∴ (-24x3 – 31x2 + 71x – 21) / (3 – 8x) = 3x2 + 5x – 7

10. 3y4 – 3y3 – 4y2 – 4y by y2 – 2y

Solution:

We have,

(3y4 – 3y3 – 4y2 – 4y) / (y2 – 2y)

By using long division method

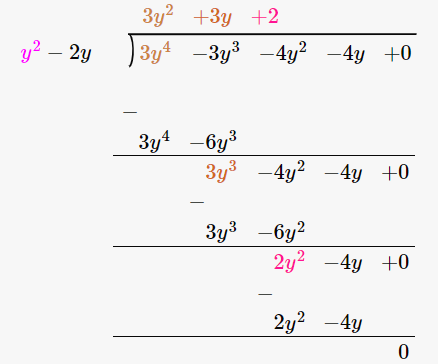
∴ (3y4 – 3y3 – 4y2 – 4y) / (y2 – 2y) = 3y2 + 3y + 2

11. 2y5 + 10y4 + 6y3 + y2 + 5y + 3 by 2y3 + 1

Solution:

We have,

(2y5 + 10y4 + 6y3 + y2 + 5y + 3) / (2y3 + 1)

By using long division method

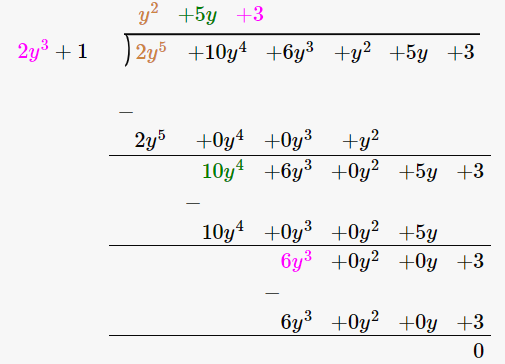
∴ (2y5 + 10y4 + 6y3 + y2 + 5y + 3) / (2y3 + 1) = y2 + 5y + 3

12. x4 – 2x3 + 2x2 + x + 4 by x2 + x + 1

Solution:

We have,

(x4 – 2x3 + 2x2 + x + 4) / (x2 + x + 1)

By using long division method

∴ (x4 – 2x3 + 2x2 + x + 4) / (x2 + x + 1) = x2 – 3x + 4

13. m3 – 14m2 + 37m – 26 by m2 – 12m + 13

Solution:

We have,

(m3 – 14m2 + 37m – 26) / (m2 – 12m + 13)

By using long division method

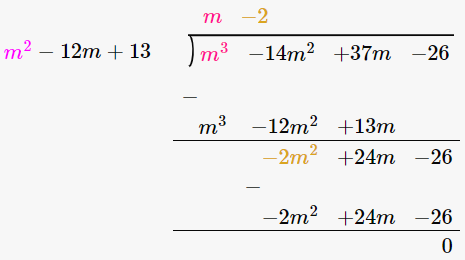
∴ (m3 – 14m2 + 37m – 26) / (m2 – 12m + 13) = m – 2

14. x4 + x2 + 1 by x2 + x + 1

Solution:

We have,

(x4 + x2 + 1) / (x2 + x + 1)

By using long division method

∴ (x4 + x2 + 1) / (x2 + x + 1) = x2 – x + 1

15. x5 + x4 + x3 + x2 + x + 1 by x3 + 1

Solution:

We have,

(x5 + x4 + x3 + x2 + x + 1) / (x3 + 1)

By using long division method

∴ (x5 + x4 + x3 + x2 + x + 1) / (x3 + 1) = x2 + x + 1

Divide each of the following and find the quotient and remainder:

16. 14x3 – 5x2 + 9x – 1 by 2x – 1

Solution:

We have,

(14x3 – 5x2 + 9x – 1) / (2x – 1)

By using long division method

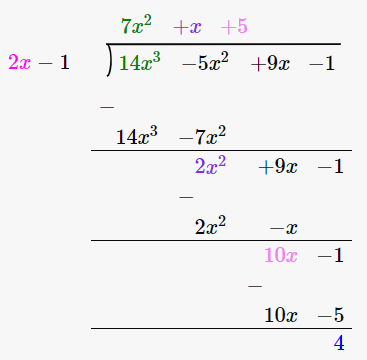
∴ Quotient is 7x2 + x + 5 and the Remainder is 4.

17. 6x3 – x2 – 10x – 3 by 2x – 3

Solution:

We have,

(6x3 – x2 – 10x – 3) / (2x – 3)

By using long division method

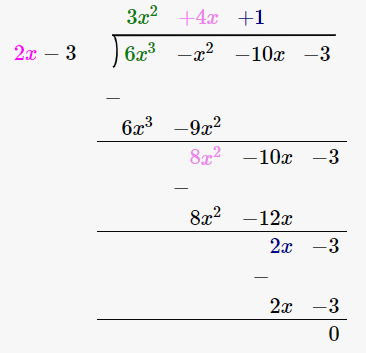
∴ Quotient is 3x2 + 4x + 1 and the Remainder is 0.

18. 6x3 + 11x2 – 39x – 65 by 3x2 + 13x + 13

Solution:

We have,

(6x3 + 11x2 – 39x – 65) / (3x2 + 13x + 13)

By using long division method

∴ Quotient is 2x – 5 and the Remainder is 0.

19. 30x4 + 11x3 – 82x2 – 12x + 48 by 3x2 + 2x – 4

Solution:

We have,

(30x4 + 11x3 – 82x2 – 12x + 48) / (3x2 + 2x – 4)

By using long division method

∴ Quotient is 10x2 – 3x – 12 and the Remainder is 0.

20. 9x4 – 4x2 + 4 by 3x2 – 4x + 2

Solution:

We have,

(9x4 – 4x2 + 4) / (3x2 – 4x + 2)

By using long division method

∴ Quotient is 3x2 + 4x + 2 and the Remainder is 0.

21. Verify division algorithm i.e. Dividend = Divisor × Quotient + Remainder, in each of the following. Also, write the quotient and remainder:

Dividend divisor

(i) 14x2 + 13x – 15 7x – 4

(ii) 15z3 – 20z2 + 13z – 12 3z – 6

(iii) 6y5 – 28y3 + 3y2 + 30y – 9 2x2 – 6

(iv) 34x – 22x3 – 12x4 – 10x2 – 75 3x + 7

(v) 15y4 – 16y3 + 9y2 – 10/3y + 6 3y – 2

(vi) 4y3 + 8y + 8y2 + 7 2y2 – y + 1

(vii) 6y4 + 4y4 + 4y3 + 7y2 + 27y + 6 2y3 + 1

Solution:

(i) Dividend divisor

14x2 + 13x – 15 7x – 4

By using long division method

Let us verify, Dividend = Divisor × Quotient + Remainder

14x2 + 13x – 15 = (7x – 4) × (2x + 3) + (-3)

= 14x2 + 21x – 8x -12 -3

= 14x2 + 13x – 15

Hence, verified.

∴ Quotient is 2x + 3 and the Remainder is -3.

(ii) Dividend divisor

15z3 – 20z2 + 13z – 12 3z – 6

By using long division method

Let us verify, Dividend = Divisor × Quotient + Remainder

15z3 – 20z2 + 13z – 12 = (3z – 6) × (5z2 + 10z/3 + 11) + 54

= 15z3 + 10z2 + 33z – 30z2 – 20z + 54

= 15z2 – 20z2 + 13z – 12

Hence, verified.

∴ Quotient is 5z2 + 10z/3 + 11 and the Remainder is 54.

(iii) Dividend divisor

6y5 – 28y3 + 3y2 + 30y – 9 2x2 – 6

By using long division method

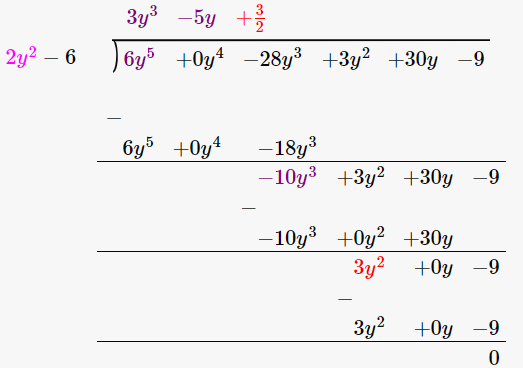
Let us verify, Dividend = Divisor × Quotient + Remainder

6y5 – 28y3 + 3y2 + 30y – 9 = (2x2 – 6) × (3y3 – 5y + 3/2) + 0

= 6y5 – 10y3 + 3y2 – 18y3 + 30y – 9

= 6y5 – 28y3 + 3y2 + 30y – 9

Hence, verified.

∴ Quotient is 3y3 – 5y + 3/2 and the Remainder is 0.

(iv) Dividend divisor

34x – 22x3 – 12x4 – 10x2 – 75 3x + 7

-12x4 – 22x3 – 10x2 + 34x – 75

By using long division method

Let us verify, Dividend = Divisor × Quotient + Remainder

-12x4 – 22x3 – 10x2 + 34x – 75 = (3x + 7) × (-4x3 + 2x2 – 8x + 30) – 285

= -12x4 + 6x3 – 24x2 – 28x3 + 14x2 + 90x – 56x + 210 -285

= -12x4 – 22x3 – 10x2 + 34x – 75

Hence, verified.

∴ Quotient is -4x3 + 2x2 – 8x + 30 and the Remainder is -285.

(v) Dividend divisor

15y4 – 16y3 + 9y2 – 10/3y + 6 3y – 2

By using long division method

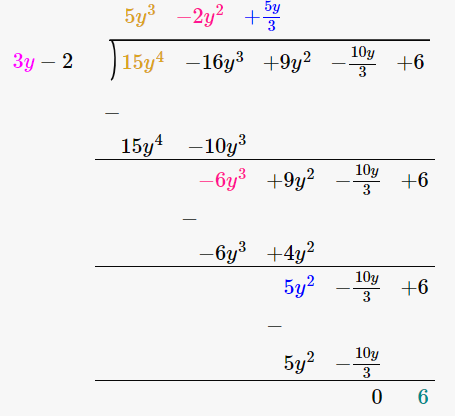
Let us verify, Dividend = Divisor × Quotient + Remainder

15y4 – 16y3 + 9y2 – 10/3y + 6 = (3y – 2) × (5y3 – 2y2 + 5y/3) + 6

= 15y4 – 6y3 + 5y2 – 10y3 + 4y2 – 10y/3 + 6

= 15y4 – 16y3 + 9y2 – 10/3y + 6

Hence, verified.

∴ Quotient is 5y3 – 2y2 + 5y/3 and the Remainder is 6.

(vi) Dividend divisor

4y3 + 8y + 8y2 + 7 2y2 – y + 1

4y3 + 8y2 + 8y + 7

By using long division method

Let us verify, Dividend = Divisor × Quotient + Remainder

4y3 + 8y2 + 8y + 7 = (2y2 – y + 1) × (2y + 5) + 11y + 2

= 4y3 + 10y2 – 2y2 – 5y + 2y + 5 + 11y + 2

= 4y3 + 8y2 + 8y + 7

Hence, verified.

∴ Quotient is 2y + 5 and the Remainder is 11y + 2.

(vii) Dividend divisor

6y5 + 4y4 + 4y3 + 7y2 + 27y + 6 2y3 + 1

By using long division method

Let us verify, Dividend = Divisor × Quotient + Remainder

6y5 + 4y4 + 4y3 + 7y2 + 27y + 6 = (2y3 + 1) × (3y2 + 2y + 2) + 4y2 + 25y + 4

= 6y5 + 4y4 + 4y3 + 3y2 + 2y + 2 + 4y2 + 25y + 4

= 6y5 + 4y4 + 4y3 + 7y2 + 27y + 6

Hence, verified.

∴ Quotient is 3y2 + 2y + 2 and the Remainder is 4y2 + 25y + 4.

22. Divide 15y4+ 16y3 + 10/3y – 9y2 – 6 by 3y – 2 Write down the coefficients of the terms in the quotient.

Solution:

We have,

(15y4+ 16y3 + 10/3y – 9y2 – 6) / (3y – 2) 

By using long division method

∴ Quotient is 5y3 + 26y2/3 + 25y/9 + 80/27

So the coefficients of the terms in the quotient are:

Coefficient of y3 = 5

Coefficient of y2 = 26/3

Coefficient of y = 25/9

Constant term = 80/27

23. Using division of polynomials state whether
(i) x + 6 is a factor of x2 – x – 42
(ii) 4x – 1 is a factor of 4x2 – 13x – 12 
(iii) 2y – 5 is a factor of 4y4 – 10y3 – 10y2 + 30y – 15
(iv) 3y2 + 5 is a factor of 6y5 + 15y4 + 16y3 + 4y2 + 10y – 35 
(v) z2 + 3 is a factor of z5 – 9z
(vi) 2x2 – x + 3 is a factor of 6x5 – x4 + 4x3 – 5x2 – x – 15

Solution:

(i) x + 6 is a factor of x2 – x – 42

Firstly let us perform long division method

Since the remainder is 0, we can say that x + 6 is a factor of x2 – x – 42

(ii) 4x – 1 is a factor of 4x2 – 13x – 12 

Firstly let us perform long division method

Since the remainder is -15, 4x – 1 is not a factor of 4x2 – 13x – 12 

(iii) 2y – 5 is a factor of 4y4 – 10y3 – 10y2 + 30y – 15

Firstly let us perform long division method

Since the remainder is 5y3 – 45y2/2 + 30y – 15, 2y – 5 is not a factor of 4y4 – 10y3 – 10y2 + 30y – 15

(iv) 3y2 + 5 is a factor of 6y5 + 15y4 + 16y3 + 4y2 + 10y – 35 

Firstly let us perform long division method

Since the remainder is 0, 3y2 + 5 is a factor of 6y5 + 15y4 + 16y3 + 4y2 + 10y – 35 

(v) z2 + 3 is a factor of z5 – 9z

Firstly let us perform long division method

Since the remainder is 0, z2 + 3 is a factor of z5 – 9z

(vi) 2x2 – x + 3 is a factor of 6x5 – x4 + 4x3 – 5x2 – x – 15

Firstly let us perform long division method

Since the remainder is 0, 2x2 – x + 3 is a factor of 6x5 – x4 + 4x3 – 5x2 – x – 15

24. Find the value of a, if x + 2 is a factor of 4x4 + 2x3 – 3x2 + 8x + 5a

Solution:

We know that x + 2 is a factor of 4x4 + 2x3 – 3x2 + 8x + 5a

Let us equate x + 2 = 0

x = -2

Now let us substitute x = -2 in the equation 4x4 + 2x3 – 3x2 + 8x + 5a

4(-2)4 + 2(-2)3 – 3(-2)2 + 8(-2) + 5a = 0

64 – 16 – 12 – 16 + 5a = 0

20 + 5a = 0

5a = -20

a = -20/5

= -4

25. What must be added to x4 + 2x3 – 2x2 + x – 1 so that the resulting polynomial is exactly divisible by x2 + 2x -3.

Solution:

Firstly let us perform long division method

By long division method we got remainder as –x + 2,

∴ x – 2 has to be added to x4 + 2x3 – 2x2 + x – 1 so that the resulting polynomial is exactly divisible by x2 + 2x -3.

EXERCISE 8.5 PAGE NO: 8.15

1. Divide the first polynomial by the second polynomial in each of the following. Also, write the quotient and remainder:

(i) 3x2 + 4x + 5, x – 2

(ii) 10x2 – 7x + 8, 5x – 3

(iii) 5y3 – 6y2 + 6y – 1, 5y – 1

(iv) x4 – x3 + 5x, x – 1

(v) y4 + y2, y2 – 2

Solution:

(i) 3x2 + 4x + 5, x – 2

By using long division method

∴ the Quotient is 3x + 10 and the Remainder is 25.

(ii) 10x2 – 7x + 8, 5x – 3

By using long division method

∴ the Quotient is 2x – 1/5 and the Remainder is 37/5.

(iii) 5y3 – 6y2 + 6y – 1, 5y – 1

By using long division method

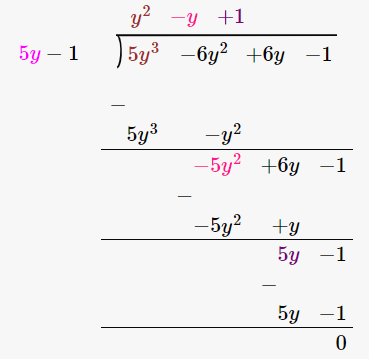
∴ the Quotient is y2 – y + 1 and the Remainder is 0.

(iv) x4 – x3 + 5x, x – 1

By using long division method

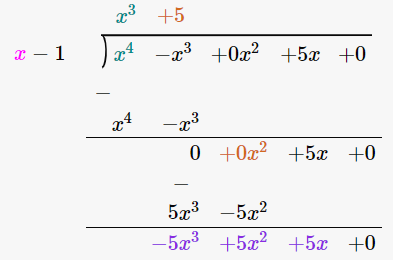
∴ the Quotient is x3 + 5 and the Remainder is 5.

(v) y4 + y2, y2 – 2

By using long division method

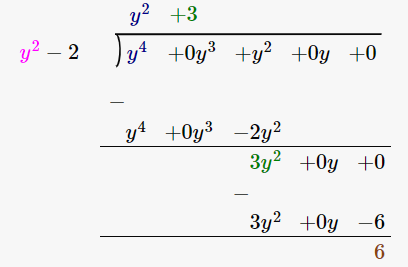
∴ the Quotient is y2 + 3 and the Remainder is 6.

2. Find Whether or not the first polynomial is a factor of the second:

(i) x + 1, 2x2 + 5x + 4

(ii) y – 2, 3y3 + 5y2 + 5y + 2

(iii) 4x2 – 5, 4x4 + 7x2 + 15

(iv) 4 – z, 3z2 – 13z + 4

(v) 2a – 3, 10a2 – 9a – 5

(vi) 4y + 1, 8y2 – 2y + 1

Solution:

(i) x + 1, 2x2 + 5x + 4

Let us perform long division method,

Since remainder is 1 therefore the first polynomial is not a factor of the second polynomial.

(ii) y – 2, 3y3 + 5y2 + 5y + 2

Let us perform long division method,

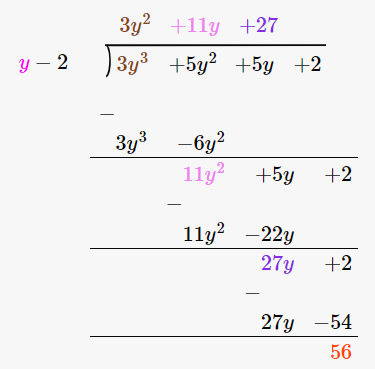
Since remainder is 56 therefore the first polynomial is not a factor of the second polynomial.

(iii) 4x2 – 5, 4x4 + 7x2 + 15

Let us perform long division method,

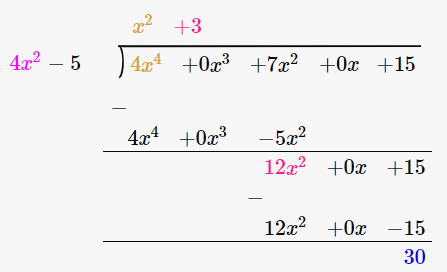
Since remainder is 30 therefore the first polynomial is not a factor of the second polynomial.

(iv) 4 – z, 3z2 – 13z + 4

Let us perform long division method,

Since remainder is 0 therefore the first polynomial is a factor of the second polynomial.

(v) 2a – 3, 10a2 – 9a – 5

Let us perform long division method,

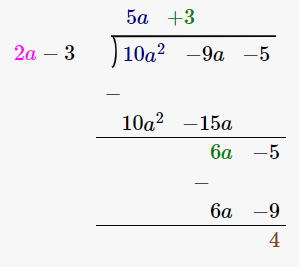
Since remainder is 4 therefore the first polynomial is not a factor of the second polynomial.

(vi) 4y + 1, 8y2 – 2y + 1

Let us perform long division method,

Since remainder is 2 therefore the first polynomial is not a factor of the second polynomial.

EXERCISE 8.6 PAGE NO: 8.17

Divide:

1. x2 – 5x + 6 by x – 3

Solution:

We have,

(x2 – 5x + 6) / (x – 3)

Let us perform long division method,

∴ the Quotient is x – 2

2. ax2 – ay2 by ax+ay

Solution:

We have,

(ax2 – ay2)/ (ax+ay)

(ax2 – ay2)/ (ax+ay) = (x – y) + 0/(ax+ay)

= (x – y)

∴ the answer is (x – y)

3. x4 – y4 by x2 – y2

Solution:

We have,

(x4 – y4)/ (x2 – y2)

(x4 – y4)/ (x2 – y2) = x2 + y2 + 0/(x2 – y2)

= x2 + y2

∴ the answer is (x2 + y2)

4. acx2 + (bc + ad)x + bd by (ax + b)

Solution:

We have,

(acx2 + (bc + ad) x + bd) / (ax + b)

(acx2 + (bc + ad) x + bd) / (ax + b) = cx + d + 0/ (ax + b)

= cx + d

∴ the answer is (cx + d)

5. (a2 + 2ab + b2) – (a2 + 2ac + c2) by 2a + b + c

Solution:

We have,[(a2 + 2ab + b2) – (a2 + 2ac + c2)] / (2a + b + c)[(a2 + 2ab + b2) – (a2 + 2ac + c2)] / (2a + b + c) = b – c + 0/(2a + b + c)

= b – c

∴ the answer is (b – c)

6. 1/4x2 – 1/2x – 12 by 1/2x – 4

Solution:

We have,

(1/4x2 – 1/2x – 12) / (1/2x – 4)

Let us perform long division method,

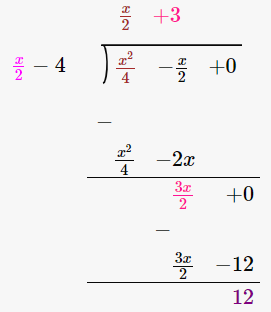
∴ the Quotient is x/2 + 3

RD Sharma Solutions for Class 8 Maths Chapter 8: Download PDF

RD Sharma Solutions for Class 8 Maths Chapter 8–Division of Algebraic Expressions

Download PDF: RD Sharma Solutions for Class 8 Maths Chapter 8–Division of Algebraic Expressions PDF

Chapterwise RD Sharma Solutions for Class 8 Maths :

About RD Sharma

RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.

R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.

Read More