RD Sharma Solutions for Class 8 Maths Chapter 5–Playing with Numbers
RD Sharma Solutions for Class 8 Maths Chapter 5–Playing with Numbers

Class 8: Maths Chapter 5 solutions. Complete Class 8 Maths Chapter 5 Notes.

RD Sharma Solutions for Class 8 Maths Chapter 5–Playing with Numbers

RD Sharma 8th Maths Chapter 5, Class 8 Maths Chapter 5 solutions

EXERCISE 5.1 PAGE NO: 5.5

1. without performing actual addition and division write the quotient when the sum of 69 and 96 is divided by
(i) 11 (ii) 15

Solution:

(i) 11

We know that 69 and 96 are having ten’s and unit’s place interchanged, i.e., they are having reverse digits.

So, sum of digits is 15.

We know that when ab + ba is divided by 11 then quotient is (a + b).

∴ The sum of 69 and 96 is divided by 11 then we get 15 (sum of digits) as our quotient.

(ii) 15

We know that 69 and 96 are having ten’s and unit’s place interchanged, i.e., they are having reverse digits.

So, sum of digits is 15.

We know that when ab + ba is divided by (a + b) then quotient is 11.

∴ The sum of 69 and 96 is divided by 15 (sum of digits) then we get 11 as our quotient.

2. Without performing actual computations, find the quotient when 94-49 is divided by
(i) 9 (ii) 5

Solution:

(i) 9

We know that 94 and 49 are having ten’s and unit’s place interchanged, i.e., they are having reverse digits.

So, difference of digits is 5.

We know that when ab – ba is divided by 9 then quotient is (a – b).

∴ 94 – 49 when divided by 9 then we get the quotient as 5.

(ii) 5

We know that 94 and 49 are having ten’s and unit’s place interchanged, i.e., they are having reverse digits.

So, difference of digits is 5.

We know that when ab – ba is divided by (a – b) then quotient is 9.

∴ The difference of 94 and 49 when divided by 5 (difference of digits) then we get 9 as our quotient.

3. If sum of the number 985 and two other numbers obtained by arranging the digits of 985 in cyclic order is divided by 111, 22 and 37 respectively. Find the quotient in each case.

Solution:

The given numbers are 985, 859 and 598.

The quotient obtained when the sum of these three numbers is divided by:

111

We know that when the sum of three digit numbers in cyclic order is done and then divided by 111, quotient is sum of digits of a number.

Quotient = Sum of digits = 22

22 (Sum of digits)

We know that when the sum of three digit numbers in cyclic order is done and then divided by sum of digits, quotient is 111.

Quotient = 111

37

Here, 3 × 37 = 111

∴ Quotient = 3 × (Sum of the digits) = 3 × 22 = 66

4. Find the quotient when the difference of 985 and 958 is divided by 9.

Solution:

The difference between the numbers 985 and 958 when divided by 9, we know that when ten’s and unit’s place is interchanged we get quotient as a difference of unit’s and ten’s place.

∴ Quotient is 8 – 5 = 3

EXERCISE 5.2 PAGE NO: 5.20

1. Given that the number

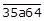
 is divisible by 3, where a is a digit, what are the possible values of a?

Solution:

We know that the given number

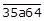
 is divisible by 3.

And, if a number is divisible by 3 then sum of digits must be a multiple of 3.

i.e., 3 + 5 + a + 6 + 4 = multiple of 3

a + 18 = 0, 3, 6, 9, 12, 15…..

Here ‘a’ is a digit, where, ‘a’ can have values between 0 and 9.

a + 18 = 18 which gives a = 0.

a + 18 = 21 which gives a = 3.

a + 18 = 24 which gives a = 6.

a + 18 = 27 which gives a = 9.

∴ a = 0, 3, 6, 9

2. If x is a digit such that the number  is divisible by 3, find possible values of x.

Solution:

We know that the given number

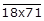
 is divisible by 3.

And, if a number is divisible by 3 then sum of digits must be a multiple of 3.

i.e., 1 + 8+ x + 7 + 1 = multiple of 3

x + 17 = 0, 3, 6, 9, 12, 15…..

Here ‘x’ is a digit, where, ‘x’ can have values between 0 and 9.

x + 17 = 18 which gives x = 1.

x + 17 = 21 which gives x = 4.

x + 17 = 24 which gives x = 7.

∴ x = 1, 4, 7

3. If x is a digit of the number such that it is divisible by 9, find possible values of x.

Solution:

We know that the given number

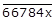
 is divisible by 9.

And, if a number is divisible by 9 then sum of digits must be a multiple of 9.

i.e., 6 + 6 + 7 + 8 + 4 + x = multiple of 9

x + 31 = 0, 9, 18, 27…..

Here ‘x’ is a digit, where, ‘x’ can have values between 0 and 9.

x + 31 = 36 which gives x = 5.

∴ x = 5

4. Given that the number  is divisible by 9, where y is a digit, what are the possible values of y?

Solution:

We know that the given number

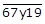
 is divisible by 9.

And, if a number is divisible by 9 then sum of digits must be a multiple of 9.

i.e., 6 + 7+ y + 1 + 9 = multiple of 9

y + 23 = 0, 9, 18, 27…..

Here ‘y’ is a digit, where, ‘y’ can have values between 0 and 9.

y + 23 = 27 which gives y = 4.

∴ y = 4

5. If  is a multiple of 11, where x is a digit, what is the value of x?

Solution:

We know that the given number

is a multiple of 11.

A number is divisible by 11 if and only if the difference between the sum of odd and even place digits is a multiple of 11.

i.e., Sum of even placed digits – Sum of odd placed digits = 0, 11, 22…

x – (3+2) = 0, 11, 22…

x – 5 is a multiple of 11

x – 5 = 0

∴ x = 5

6. If is a number with x as its tens digit such that it is divisible by 4. Find all possible values of x.

Solution:

We know that the given number

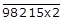
 is divisible by 4.

A number is divisible by 4 only when the number formed by its digits in unit’s and ten’s place is divisible by 4.

i.e., x2 is divisible by 4

Expanding x2,

10x + 2 = multiple of 4

Here x2 can take values 2, 12, 22, 32, 42, 52, 62, 72, 82, 92

So values 12, 32, 52, 72 and 92 are divisible by 4.

∴ x can take values 1,3,5,7 and 9

7. If x denotes the digit at hundreds place of the number such that the number is divisible by 11. Find all possible values of x.

Solution:

We know that the given number

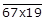
is divisible by 11.

A number is divisible by 11 if and only if the difference between the sum of odd and even place digits is a multiple of 11.

i.e., Sum of even placed digits – Sum of odd placed digits = 0, 11, 22…

(6 + x + 9) – (7+1) = 0, 11, 22…

x + 7 is a multiple of 11

x + 7 = 11

∴ x = 4

8. Find the remainder when 981547 is divided by 5. Do that without doing actual division.

Solution:

We know that if a number is divided by 5, then remainder is obtained by dividing just the unit place by 5.

i.e., 7 ÷ 5 gives 2 as a remainder.

∴ Remainder will be 2 when 981547 is divided by 5.

9. Find the remainder when 51439786 is divided by 3. Do that without performing actual division.

Solution:

We know that if a number is divided by 3, then remainder is obtained by dividing sum of digits by 3.

Here, sum of digits (5+1+4+3+9+7+8+6) is 43.

i.e., 43 ÷ 3 gives 1 as a remainder.

∴ Remainder will be 1 when 51439786 is divided by 3.

10. Find the remainder, without performing actual division, when 798 is divided by 11.

Solution:

We know that if a number is divided by 11, then remainder is difference between sum of even and odd digit places.

i.e., Remainder = 7 + 8 – 9 = 6

∴ Remainder will be 6 when 798 is divided by 11.

11. Without performing actual division, find the remainder when 928174653 is divided by 11.

Solution:

We know that if a number is divided by 11, then remainder is difference between sum of even and odd digit places.

i.e., Remainder = 9 + 8 + 7 + 6 + 3 – 2 – 1 – 4 – 5 = 33 – 12 = 21

∴ 21 ÷ 11 gives 10 as remainder

∴ Remainder will be 10 when 928174653 is divided by 11.

12. Given an example of a number which is divisible by
(i) 2 but not by 4.
(ii) 3 but not by 6.
(iii) 4 but not by 8.
(iv) Both 4 and 8 but not by 32

Solution:

(i) 2 but not by 4.

Any number which follows the formula of 4n + 2 is an example of a number divisible by 2 but not by 4.

i.e., 10 where n = 1.

(ii) 3 but not by 6.

Any number which follows the formula of 6n + 3 is an example of a number divisible by 3 but not by 6.

i.e., 15 where n = 1.

(iii) 4 but not by 8.

Any number which follows the formula of 8n + 4 is an example of a number divisible by 4 but not by 8.

i.e., 28 where n = 1.

(iv) Both 4 and 8 but not by 32

Any number which follows the formula of 32n + 8 or 32n + 16 or 32n +24 is an example of a number divisible by both 4 and 8 but not by 32.

i.e., 48 where n = 1.

13. Which of the following statements are true?
(i) If a number is divisible by 3, it must be divisible by 9.
(ii) If a number is divisible by 9, it must by divisible by 3.
(iii) If a number is divisible by 4, it must by divisible by 8.
(iv) If a number is divisible by 8, it must be divisible by 4.
(v) A number is divisible by 18, if it is divisible by both 3 and 6.
(vi) If a number is divisible by both 9 and 10, it must be divisible by 90.
(vii) If a number exactly divides the sum of two numbers, it must exactly divide the numbers separately.
(viii) If a number divides three numbers exactly, it must divide their sum exactly.
(ix) If two numbers are co-prime, at least one of them must be a prime number.
(x) The sum of two consecutive odd numbers is always divisible by 4.

Solution:

(i) If a number is divisible by 3, it must be divisible by 9.

False

Because any number which follows the formula 9n + 3 or 9n + 6 violates the statement.

For example: 6, 12…

(ii) If a number is divisible by 9, it must by divisible by 3.

True

Because 9 is multiple of 3, any number divisible by 9 is also divisible by 3.

(iii) If a number is divisible by 4, it must by divisible by 8.

False

Because any number which follows the formula 8n + 4 violates the statement.

For example: 4, 12, 20….

(iv) If a number is divisible by 8, it must be divisible by 4.

True

Because 8 is multiple of 4, any number divisible by 8 is also divisible by 4.

(v) A number is divisible by 18, if it is divisible by both 3 and 6.

False

Because for example 24, this is divisible by both 3 and 6 but not divisible by 18.

(vi) If a number is divisible by both 9 and 10, it must be divisible by 90.

True

Because 90 is the GCD of 9 and 10, any number divisible by both 9 and 10 is also divisible by 90.

(vii) If a number exactly divides the sum of two numbers, it must exactly divide the numbers separately.

False

Because let us consider an example 6 divide 30, but 6 divides none of 13 and 17 as both are prime numbers.

(viii) If a number divides three numbers exactly, it must divide their sum exactly.

True

Because if x, y and z are three numbers, each of x, y and z is divided by a number (say q), then (x + y + z) is also divisible by q.

(ix) If two numbers are co-prime, at least one of them must be a prime number.

False

Because 16 and 21 are co-prime but none of them is prime.

(x) The sum of two consecutive odd numbers is always divisible by 4.

True

Because 3+5=8 which is divisible by 4.

EXERCISE 5.3 PAGE NO: 5.30

Solve each of the following Cryptarithms:
1.

Solution:

Firstly let us solve for unit’s place,

7 + B = A

And for ten’s place,

3 + A = 9

Which means that A = 6 and B = -1 which is not possible.

So, there should be one carry in ten’s place which means 7 + B >9

Now solving for ten’s place with one carry,

3 +A +1 = 9

A = 9-1-3 = 5

For unit’s place subtracting 10 as one carry is given to ten’s place,

7 + B – 10= 5

B = 5+10-7 = 8

∴A = 5 and B = 8

2.

Solution:

Firstly let us solve for unit’s place,

B + 7 = A

And for ten’s place,

A + 3 = 9

Which means that A = 6 and B = -1 which is not possible.

So, there should be one carry in ten’s place, which means B + 7 >9

Now solving for ten’s place with one carry,

A +3 +1 = 9

A = 9-4 = 5

For unit’s place subtracting 10 as one carry is given to ten’s place,

B + 7 – 10= 5

B = 5+10-7 = 8

∴ A = 5 and B = 8

3.

Solution:

Firstly let us solve for unit’s place,

1 + B = 0

Which means that B = -1 which is not possible.

So, there should be one carry in ten’s place,

A + 1 +1 = B —- (1)

For unit’s place, we need to subtract 10 as one carry is given in ten’s place,

1 + B – 10 = 0

B = 10-1 = 9

Substituting B = 9 in (1),

A + 1 + 1 = 9

A = 9-1-1 = 7

∴ A = 7 and B = 9

4.

Solution:

Firstly let us solve for unit’s place,

B + 1 = 8

B = 7

Now let us solve for ten’s place,

A + B = 1

A + 7 = 1

A = -6 which is not possible.

Hence, A + B > 9

We know that now there should be one carry in hundred’s place and so we need to subtract 10 from ten’s place,

i.e., A + B – 10 = 1

A + 7 = 11

A = 11-7 = 4

Now to check whether our values of A and B are correct, we should solve for hundred’s place.

2 + A + 1 = B

2 + 4 + 1 = 7

7 = 7

i.e., RHS = LHS

∴ A = 4 and B = 7

5.

Solution:

Firstly let us solve for unit’s place,

A + B = 9 —- (1)

With this condition we know that sum of 2 digits can be greater than 18.

So, there is no need to carry one from ten’s place.

Now let us solve for ten’s place,

2 + A = 0

Which means A = -2 which is never possible

Hence, 2 + A > 9

Now, there should be one carry in hundred’s place and hence we need to subtract 10 from ten’s place,

i.e., 2 + A – 10 = 0

A = 10-2 = 8

Now, substituting A=8 in 1,

A + B = 9

8 + B = 9

B = 9 – 8

B = 1

∴ A = 8 and B = 1

6.

Solution:

Firstly let us solve for unit’s place,

We have two conditions here, 7 + B ≤ 9 and 7 + B > 9

For 7 + B ≤ 9

7 + B = A

A – B = 7 —- (1)

Now let us solve for ten’s place,

B + A = 8 —- (2)

Solving 1 and 2 simultaneously,

2A = 15 which means A = 7.5 which is not possible

So, our condition 7 + B ≤ 9 is wrong.

∴ 7 + B > 9 is correct condition

Hence, there should be one carry in ten’s place and subtracting 10 from unit’s place,

7 + B – 10 = A

B – A = 3 —- (3)

For ten’s place,

B + A + 1 = 8

B + A = 8-1

B + A = 7 —- (4)

Solving (3) and (4) simultaneously,

2B = 10

B = 10/2 = 5

Substituting the value of B in equation 4

B + A = 7

5 + A = 7

A = 7-5 = 2

∴ B = 5 and A = 2

7. Show that the Cryptarithm does not have any solution.

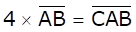
Solution:

If B is multiplied by 4 then only 0 satisfies the above condition.

So, for unit place to satisfy the above condition, we should have B = 0.

Similarly for ten’s place, only 0 satisfies the above condition.

But, AB cannot be 00 as 00 is not a two digit number.

So, A and B cannot be equal to 0

∴ there is no solution satisfying the condition

RD Sharma Solutions for Class 8 Maths Chapter 5: Download PDF

RD Sharma Solutions for Class 8 Maths Chapter 5–Playing with Numbers

Download PDF: RD Sharma Solutions for Class 8 Maths Chapter 5–Playing with Numbers PDF

Chapterwise RD Sharma Solutions for Class 8 Maths :

About RD Sharma

RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.

R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.

Read More