Class 7: Maths Chapter 18 solutions. Complete Class 7 Maths Chapter 18 Notes.
Contents
RD Sharma Solutions for Class 7 Maths Chapter 18–Symmetry
RD Sharma 7th Maths Chapter 18, Class 7 Maths Chapter 18 solutions
Exercise 18.1 Page No: 18.6
1. State the number of lines of symmetry for the following figures:
(i) An equilateral triangle
(ii) An isosceles triangle
(iii) A scalene triangle
(iv) A rectangle
(v) A rhombus
(vi) A square
(vii) A parallelogram
(viii) A quadrilateral
(ix) A regular pentagon
(x) A regular hexagon
(xi) A circle
(xii) A semi-circle
Solution:
(i) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore an equilateral triangle has 3 lines of symmetry.
(ii) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore an isosceles triangle has 1 line of symmetry.
(iii) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a scalene triangle has no line of symmetry.
(iv) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a rectangle has 2 lines of symmetry.
(v) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a rhombus has 2 lines of symmetry.
(vi) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a square has 4 lines of symmetry.
(vii) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a parallelogram has no line of symmetry.
(viii) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a quadrilateral has no line of symmetry.
(ix) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a regular pentagon has 5 lines of symmetry.
(x) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a regular hexagon has 6 lines of symmetry.
(xi) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a circle has an infinite number of lines of symmetry all along the diameters.
(xii) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a semicircle has only one line of symmetry.
2. What other name can you give to the line of symmetry of
(i) An isosceles triangle?
(ii) A circle?
Solution:
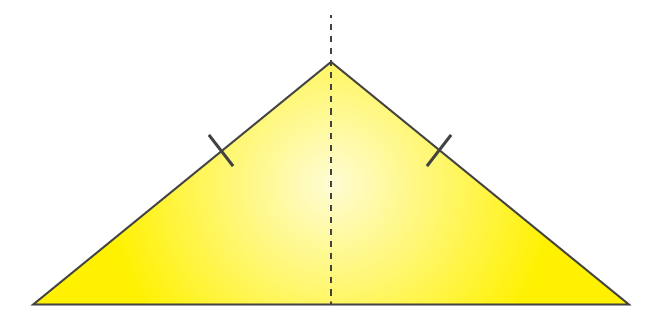
(i) An isosceles triangle has only 1 line of symmetry. This line of symmetry is also known as the altitude of an isosceles triangle.
(ii) A circle has infinite lines of symmetry all along its diameters.

3. Identify three examples of shapes with no line of symmetry.
Solution:



A scalene triangle, a parallelogram and a trapezium do not have any line of symmetry.
4. Identify multiple lines of symmetry, if any, in each of the following figures:
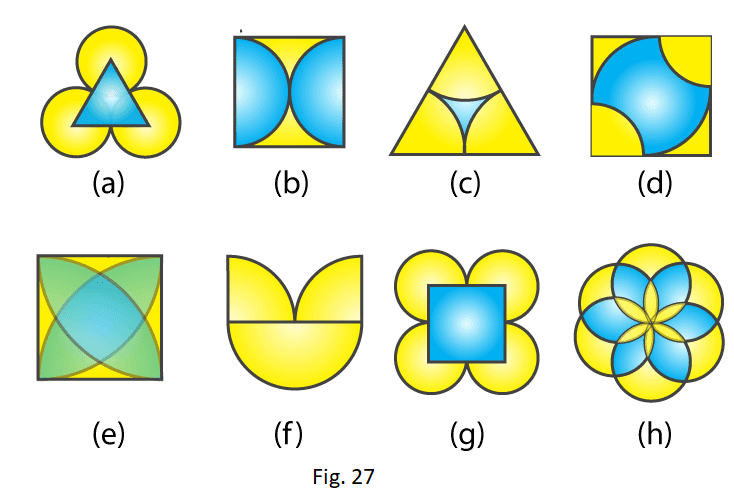
Solution:
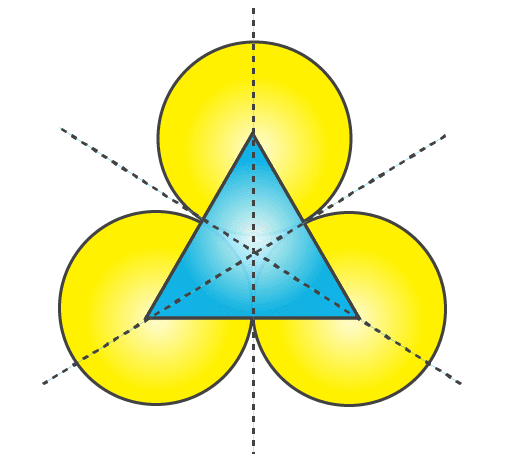
(a)The given figure has 3 lines of symmetry. Therefore it has multiple lines of symmetry.
(b) The given figure has 2 lines of symmetry. Therefore it has multiple lines of symmetry.

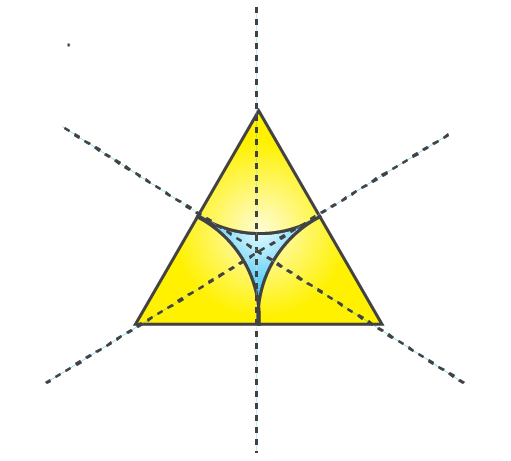
(c) The given figure has 3 lines of symmetry. Therefore it has multiple lines of symmetry.
(d) The given figure has 2 lines of symmetry. Therefore it has multiple lines of symmetry.
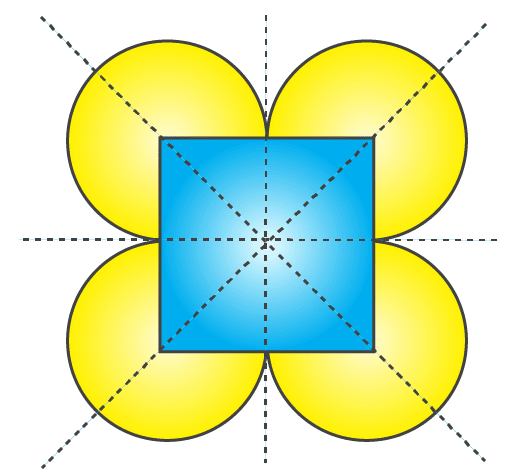
(e) The given figure has 4 lines of symmetry. Therefore it has multiple lines of symmetry.

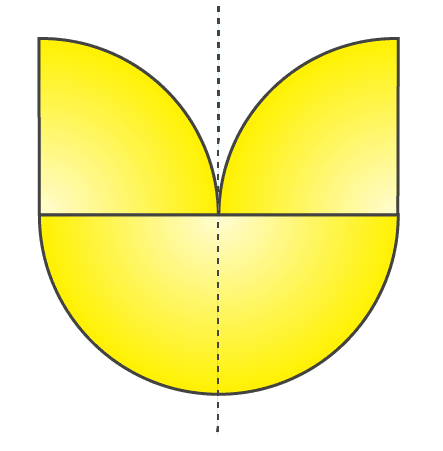
(f) The given figure has only 1 line of symmetry.
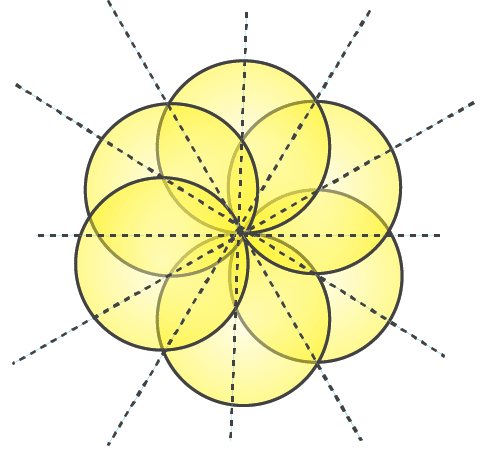
(g) The given figure has 4 lines of symmetry. Therefore it has multiple lines of symmetry.
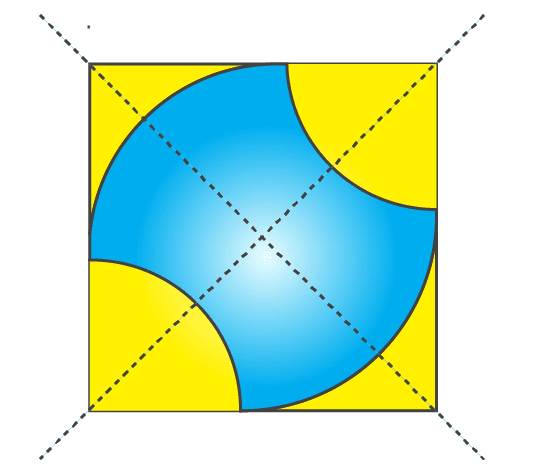
(h) The given figure has 6 lines of symmetry. Therefore it has multiple lines of symmetry.
Exercise 18.2 Page No: 18.8
1. In the following figures, the mirror line (i.e. the line of symmetry) is given as dotted line. Complete each figure performing reflection in the dotted (mirror) line. Also, try to recall name of the complete figure.
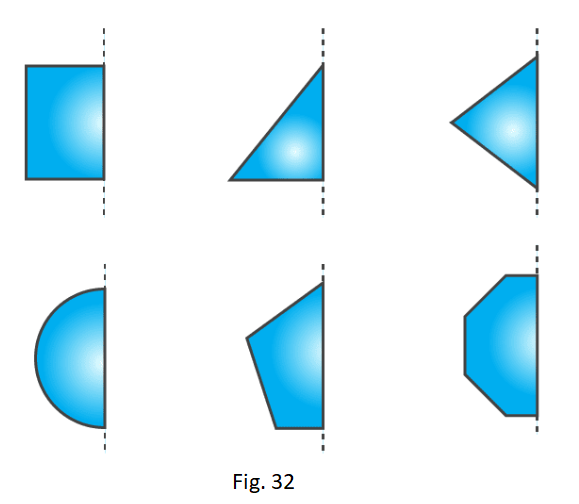
Solution:
(a) It will be a rectangle.

(b) It will be triangle
(c) It will be rhombus

(d) It will be circle

(e) It will be pentagon

(d) It will be octagon

2. Each of the following figures shows paper cuttings with punched holes. Copy these figures on a plane sheet and mark the axis of symmetry so that if the paper is folded along it, then the wholes on one side of it coincide with the holes on the other side.
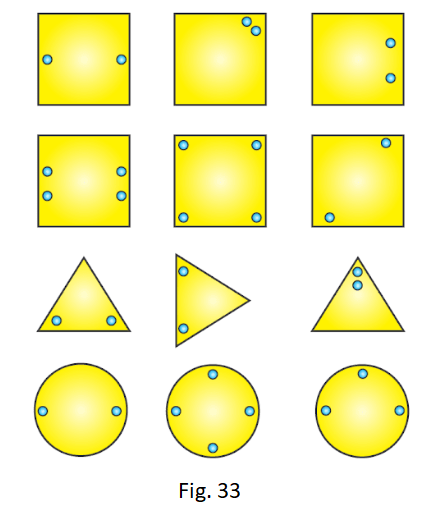
Solution:
The lines of symmetry in the given figures are as follows:

3. In the following figures if the dotted lines represent the lines of symmetry, find the other hole(s).
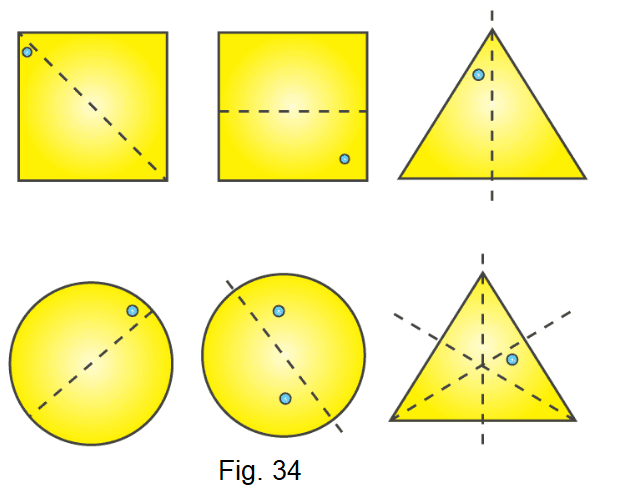
Solution:
The other holes in the figure are as follows:

Exercise 18.3 Page No: 18.16
1. Give the order of rotational symmetry for each of the following figures when rotated about the marked point (x):
Solution:
(i) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 4.
(ii) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 3.
(iii) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 3.
(iv) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 4.
(v) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 2.
(vi) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 4.
(vii) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 5.
(viii) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 6.
(ix) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 3.
2. Name any two figures that have both line symmetry and rotational symmetry.
Solution:
An equilateral triangle and a square have both lines of symmetry and rotational symmetry.

3. Give an example of a figure that has a line of symmetry but does not have rotational symmetry.
Solution:
A semicircle and an isosceles triangle have a line of symmetry but do not have rotational symmetry.

4. Give an example of a geometrical figure which has neither a line of symmetry nor a rotational symmetry.
Solution:
A scalene triangle has neither a line of symmetry nor a rotational symmetry.

5. Give an example of a letter of the English alphabet which has
(i) No line of symmetry
(ii) Rotational symmetry of order 2.
Solution:
(i) The letter of the English alphabet which has no line of symmetry is Z.
(ii) The letter of the English alphabet which has rotational symmetry of order 2 is N.
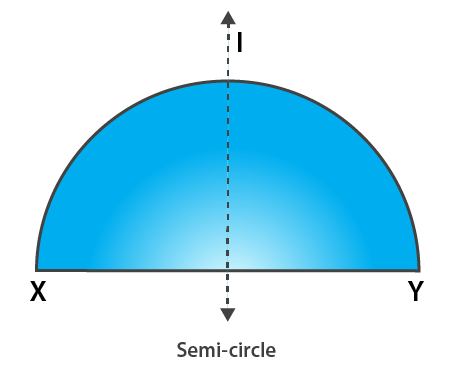
6. What is the line of symmetry of a semi-circle? Does it have rotational symmetry?
Solution:
A semicircle (half of a circle) has only one line of symmetry. In the figure, there is one line of symmetry. The figure is symmetric along the perpendicular bisector I of the diameter XY. A semi-circle does not have any rotational symmetry.
7. Draw, whenever possible, a rough sketch of
(i) a triangle with both line and rotational symmetries.
(ii) a triangle with only line symmetry and no rotational symmetry.
(iii) a quadrilateral with a rotational symmetry but not a line of symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry.
Solution:
(i) An equilateral triangle has 3 lines of symmetry and a rotational symmetry of order 3.

(ii) An isosceles triangle has only 1 line of symmetry and no rotational symmetry.

(iii) A parallelogram is a quadrilateral which has no line of symmetry but a rotational symmetry of order 2.

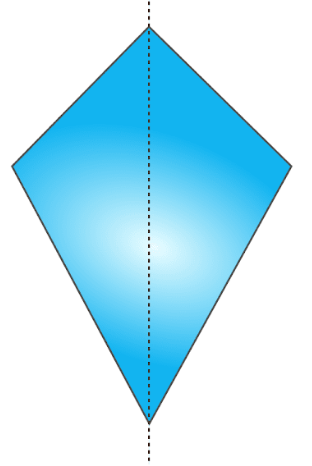
(iv) A kite is a quadrilateral which has only one line of symmetry and no rotational symmetry.
8. Fill in the blanks:
| Figures | Centre of rotation | Order of rotation | Angle of rotation |
| Square | |||
| Rectangle | |||
| Rhombus | |||
| Equilateral Triangle | |||
| Regular hexagon | |||
| Circle | |||
| Semi-circle |
Solution:
| Figures | Centre of rotation | Order of rotation | Angle of rotation |
| Square | Point of intersection of the line segments joining the mid-points of opposite sides. | 4 | 90o |
| Rectangle | Point of intersection of the line segments joining the mid-points of opposite sides | 2 | 180o |
| Rhombus | Point of intersection of diagonals | 2 | 180o |
| Equilateral Triangle | Point of intersection of angle bisectors i.e., centroid | 3 | 1200 |
| Regular hexagon | Centre of the hexagon | 6 | 60o |
| Circle | Centre of the circle | Unlimited | Any angle |
| Semi-circle | Nil | Nil | Nil |
9. Fill in the blanks:
| English Alphabet Letter | Line Symmetry | Number of Lines of Symmetry | Rotational symmetry | Order of rotational symmetry |
| Z | Nil | 0 | Yes | 2 |
| S | – | – | – | – |
| H | Yes | – | Yes | – |
| O | Yes | – | Yes | – |
| E | Yes | – | – | – |
| N | – | – | Yes | – |
| C | – | – | – | – |
Solution:
| English Alphabet Letter | Line Symmetry | Number of Lines of Symmetry | Rotational symmetry | Order of rotational symmetry |
| Z | Nil | 0 | Yes | 2 |
| S | Nil | 0 | Yes | 2 |
| H | Yes | 2 | Yes | 2 |
| O | Yes | 4 | Yes | 2 |
| E | Yes | 1 | No | 0 |
| N | Nil | 0 | Yes | 2 |
| C | Yes | 1 | No | 0 |
RD Sharma Solutions for Class 7 Maths Chapter 18: Download PDF
RD Sharma Solutions for Class 7 Maths Chapter 18–Symmetry
Download PDF: RD Sharma Solutions for Class 7 Maths Chapter 18–Symmetry PDF
Chapterwise RD Sharma Solutions for Class 7 Maths :
- Chapter 1–Integers
- Chapter 2–Fractions
- Chapter 3–Decimals
- Chapter 4–Rational Numbers
- Chapter 5–Operations On Rational Numbers
- Chapter 6–Exponents
- Chapter 7–Algebraic Expressions
- Chapter 8–Linear Equations in One Variable
- Chapter 9–Ratio And Proportion
- Chapter 10–Unitary Method
- Chapter 11–Percentage
- Chapter 12–Profit And Loss
- Chapter 13–Simple Interest
- Chapter 14–Lines And Angles
- Chapter 15–Properties of Triangles
- Chapter 16–Congruence
- Chapter 17–Constructions
- Chapter 18–Symmetry
- Chapter 19–Visualising Solid Shapes
- Chapter 20–Mensuration – I (Perimeter and area of rectilinear figures)
- Chapter 21–Mensuration – II (Area of Circle)
- Chapter 22–Data Handling – I (Collection and Organisation of Data)
- Chapter 23–Data Handling – II Central Values
- Chapter 24–Data Handling – III (Constructions of Bar Graphs)
- Chapter 25–Data Handling – IV (Probability)
About RD Sharma
RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.
R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.
