RD Sharma Solutions for Class 6 Maths Chapter 11–Angles
RD Sharma Solutions for Class 6 Maths Chapter 11–Angles

Class 6: Maths Chapter 11 solutions. Complete Class 6 Maths Chapter 11 Notes.

RD Sharma Solutions for Class 6 Maths Chapter 11–Angles

RD Sharma 6th Maths Chapter 11, Class 6 Maths Chapter 11 solutions

Exercise 11.1 page: 11.5

1. Give three examples of angles from your environment.

Solution:

The three examples of angles are

The angle formed by the two adjacent fingers of our hand

The angle formed by two adjacent walls of a room

The angle formed by the hour hand and minute hand of a clock.

2. Write the arms and the vertex of ∠ LMP given in Fig. 11.14.

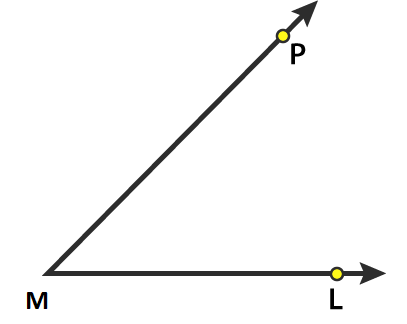
Solution:

The vertex of ∠ LMP is M and the arms are ML and MP.

3. How many angles are formed in the figures 11.15 (i), (ii) and (iii)? Name them.

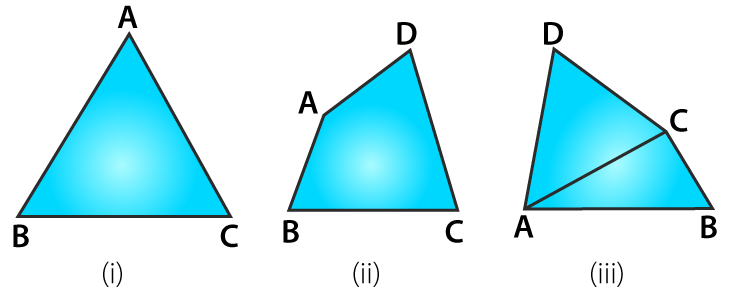
Solution:

(i) Three angles are formed in figure (i) namely ∠ ABC, ∠ ACB and ∠ BAC.

(ii) Four angles are formed in figure (ii) namely ∠ ABC, ∠ BCD, ∠ CDA and ∠ DAB.

(iii) Eight angles are formed in figure (iii) namely ∠ ABC, ∠ BCD, ∠ CDA, ∠ DAB, ∠ CAB, ∠ CAD, ∠ BCA and ∠ ACD.

4. In Fig. 11.16, list the points which are: (i) in the interior of ∠ P (ii) in the exterior of ∠ P and (iii) lie on ∠ P.

Solution:

(i) The points which are in the interior of ∠ P are J and C.

(ii) The points which are in the exterior of ∠ P are B and D.

(iii) The points which lie on ∠ P are A, P and M.

5. In Fig. 11.17, write another name for:

(i) ∠ 1

(ii) ∠ 2

(iii) ∠ 3

(iv) ∠ 4

Solution:

(i) From the figure, another name for ∠ 1 is ∠ BOD or ∠ DOB.

(ii) From the figure, another name for ∠ 2 is ∠ BOC or ∠ COB.

(iii) From the figure, another name for ∠ 3 is ∠ COA or ∠ AOC.

(iv) From the figure, another name for ∠ 4 is ∠ AOD or ∠ DOA.

6. In Fig. 11.18, write another name for:

(i) ∠ 1

(ii) ∠ 2

(iii) ∠ 3

Solution:

(i) From the figure, another name for ∠ 1 is ∠ EPB or ∠ BPE.

(ii) From the figure, another name for ∠ 2 is ∠ CQP or ∠ PQC.

(iii) From the figure, another name for ∠ 3 is ∠ DQF or ∠ FQD.

7. In Fig. 11.19, which of the following statements are true:

(i) Point B is the interior of ∠ AOB.

(ii) Point B is the interior of ∠ AOC.

(iii) Point A is the interior of ∠ AOD.

(iv) Point C is the exterior of ∠ AOB.

(v) Point D is the exterior of ∠ AOC.

Solution:

(i) False. B lies on ∠ AOB.

(ii) True

(iii) False. A lies on ∠ AOD.

(iv) True

(v) True

8. Which of the following statements are true:

(i) The vertex of an angle lies in its interior.

(ii) The vertex of an angle lies in its exterior.

(iii) The vertex of an angle lies on it.

Solution:

(i) False.

(ii) False.

(iii) True.

9. By simply looking at the pair of angles given in Fig. 11.20, state which of the angles in each of the pairs is greater:

Solution:

(i) From the figure we know that ∠ AOB > ∠ DEF.

(ii) From the figure we know that ∠ PQR > ∠ LMN.

(iii) From the figure we know that ∠ UVW > ∠ XYZ.

10. By using tracing paper compare the angles in each of the pairs given in Fig. 11.21.

Solution:

(i) From the figure we know that ∠ PQR > ∠ AOB.

(ii) From the figure we know that ∠ UVW > ∠ LMN.

(iii) From the figure we know that ∠ RST > ∠ XYZ.

(iv) From the figure we know that ∠ PQR > ∠ EFG.

Exercise 11.2 page: 11.10

1. Give two examples each of right, acute and obtuse angles from your environment.

Solution:

The two examples of right angle are:

Two adjacent walls of a room and adjacent edges of a book

The two examples of acute angle are:

Two adjacent sides of the letter Z and two adjacent fingers of our hand.

The two examples of obtuse angles are:

Two sloping sides of a roof and two adjacent blades of a fan.

2. An angle is formed by two adjacent fingers. What kind of angle will it appear?

Solution:

The angle formed by two adjacent fingers will appear as acute angle.

3. Shikha is rowing a boat due north-east. In which direction will she be rowing if she turns it through:

(i) a straight angle

(ii) a complete angle.

Solution:

(i) If she turns through a straight angle (180o) she will be rowing in the South-West direction.

(ii) If she turns through a complete angle (360o) she will be rowing in North-East direction.

4. What is the measure of the angle in degrees between:

(i) North and West?

(ii) North and South?

(iii) North and South- East?

Solution:

The measure of the angle in degrees between:

(i) North and West is 90o.

(ii) North and South is 180o.

(iii) North and South-East is 135o.

5. A ship sailing in river Jhelam moves towards east. If it changes to north, through what angle does it turn?

Solution:

It the ship moves from east to north direction, the angle it turns is 90o.

6. You are standing in a class-room facing north. In what direction are you facing after making a quarter turn?

Solution:

By making a quarter turn (90o), I will be facing towards east if I turn to my right hand and if I turn to my left hand, I will be facing towards west.

7. A bicycle wheel makes four and a half turns. Find the number of right angles through which it turns.

Solution:

We know that the wheel of a bicycle covers 360o in one turn.

It can be written as

360/90 = 4 right angles

We know that in four and half turns the wheel turns by 4 (4.5) = 18 right angles

Hence, the number of right angles through which it turns is 18.

8. Look at your watch face. Through how many right angles does the minute-hand moves between 8: 00 O’ clock and 10: 30 O’ clock?

Solution:

We know that the time interval between 8: 00 O’ clock and 10: 30 O’ clock is two and half hours

The minute hand turns 360o in 1 hour

360/90 = 4 right angles

So in two and half hours the minute hand turns by 2.5 (4) = 10 right angles.

Hence, the minute hand turns by 10 right angles.

9. If a bicycle wheel has 48 spokes, then find the angle between a pair of adjacent spokes.

Solution:

The central angle in a bicycle is 360o which consists of 48 spokes.

So the angle between a pair of adjacent spokes = 360/48 = 7.5o

Hence, the angle between a pair of adjacent spokes is 7.5o.

10. Classify the following angles as acute, obtuse, straight, right, zero and complete angle:

(i) 118o

(ii) 29o

(iii) 145o

(iv) 165o

(v) 0o

(vi) 75o

(vii) 180o

(viii) 89.5o

(ix) 30o

(x) 90o

(xi) 179o

(xii) 360o

(xiii) 90 ½ o

Solution:

(i) 118o is an obtuse angle.

(ii) 29o is an acute angle.

(iii) 145o is an obtuse angle.

(iv) 165o is an obtuse angle.

(v) 0o is a zero angle.

(vi) 75o is an acute angle.

(vii) 180o is a straight angle.

(viii) 89.5o is an acute angle.

(ix) 30o is an acute angle.

(x) 90o is a right angle.

(xi) 179o is an obtuse angle.

(xii) 360o is a complete angle.

(xiii) 90 ½ o is an obtuse angle.

11. Using only a ruler, draw an acute angle, a right angle and an obtuse angle in your notebook and name them.

Solution:

12. State the kind of angle, in each case, formed between the following directions:

(i) East and West

(ii) East and North

(iii) North and North-East

(iv) North and South-East

Solution:

(i) East and West directions form a straight angle (180o).

(ii) East and North directions form a right angle (90o).

(iii) North and North-East directions form an acute angle (45o).

(iv) North and South-East directions form an obtuse angle (135o).

13. State the kind of each of the following angles:

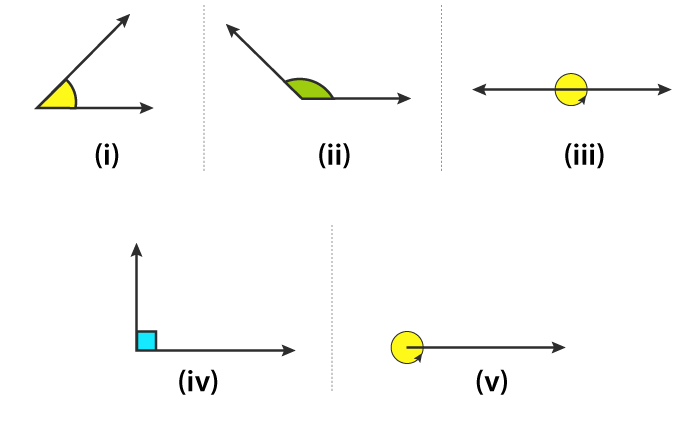
Solution:

(i) Acute angle which measures between 0o and 90o.

(ii) Obtuse angle which measures between 90o and 180o.

(iii) Straight angle which measures 180o.

(iv) Right angle which measures 90o.

(v) Complete angle which measures 360o.

Objective Type Questions page: 11.11

Mark the correct alternative in each of the following:

1. The vertex of an angles lies
(a) in its interior
(b) in its exterior
(c) on the angle
(d) inside the angle

Solution:

The option (c) is the correct answer.

The vertex of an angles lies on the angle.

2. The figure formed by two rays with the same initial point is known as
(a) a ray
(b) a line
(c) an angle
(d) a line segment

Solution:

The option (c) is the correct answer.

The figure formed by two rays with the same initial point is known as an angle.

3. An angle of measure 0° is called
(a) a complete angle
(b) a right angle
(c) a straight angle
(d) None of these

Solution:

The option (d) is the correct answer.

An angle of measure 0° is called a zero angle.

4. An angle of measure 90° is called
(a) a complete angle
(b) a right angle
(c) a straight angle
(d) a reflex angle

Solution:

The option (b) is the correct answer.

An angle of measure 90° is called a right angle.

5. An angle of measure 180° is called
(a) a zero angle
(b) a right angle
(c) a straight angle
(d) a reflex angle

Solution:

The option (c) is the correct answer.

An angle of measure 180° is called a straight angle.

6. An angle of measure 360° is called
(a) a zero angle
(b) a straight angle
(c) a reflex angle
(d) a complete angle

Solution:

The option (d) is the correct answer.

An angle of measure 360° is called a complete angle.

7. An angle of measure 240° is
(a) an acute angle
(b) an obtuse angle
(c) a straight angle
(d) a complete angle

Solution:

There is no correct answer.

An angle of measure 240° is called a reflex angle.

8. A reflex angle measures
(a) more than 90° but less than 180°
(b) more than 180° but less than 270°
(c) more than 180° but less than 360°
(d) None of these

Solution:

The option (c) is the correct answer.

A reflex angle measures more than 180° but less than 360°.

9. The number of degrees in 2 right angle is
(a) 90°
(b) 180°
(c) 270°
(d) 360°

Solution:

The option (b) is the correct answer.

The number of degrees in 2 right angle is 180°.

10. The number of degrees in 3/2 right angles is
(a) 180°
(b) 360°
(c) 270°
(d) 90°

Solution:

There is no correct answer.

One right angle = 90°

So 3/2 right angles = 3/2 (90°) = 135o

11. If a bicycle wheel has 36 spokes, then the angle between a pair of adjacent spokes is
(a) 10°
(b) 15°
(c) 20°
(d) 12°

Solution:

The option (a) is the correct answer.

The central angle of a bicycle wheel measures 360°

The angle between a pair of adjacent spokes of the wheel which has 36 spokes = 360/ 36 = 10o

RD Sharma Solutions for Class 6 Maths Chapter 11: Download PDF

RD Sharma Solutions for Class 6 Maths Chapter 11–Angles

Download PDF: RD Sharma Solutions for Class 6 Maths Chapter 11–Angles PDF

Chapterwise RD Sharma Solutions for Class 6 Maths :

About RD Sharma

RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.

R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.

Read More