RD Sharma Solutions for Class 6 Maths Chapter 15–Pair of Lines and Transversal
RD Sharma Solutions for Class 6 Maths Chapter 15–Pair of Lines and Transversal

Class 6: Maths Chapter 15 solutions. Complete Class 6 Maths Chapter 15 Notes.

RD Sharma Solutions for Class 6 Maths Chapter 15–Pair of Lines and Transversal

RD Sharma 6th Maths Chapter 15, Class 6 Maths Chapter 15 solutions

Exercise 15.1 page: 15.2

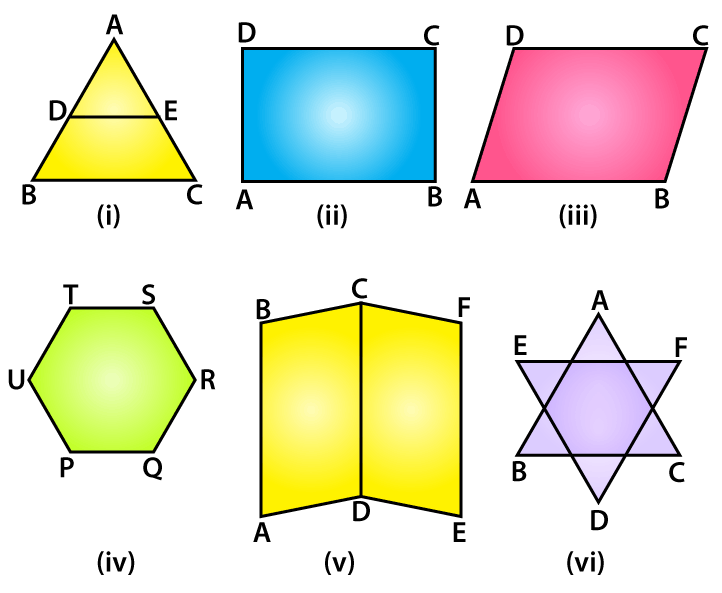
1. Identify parallel line segments shown in Fig. 15.6.

Solution:

(i) From the figure we know that BC || DE.

(ii) From the figure we know that AB || DC, AD || BC.

(iii) From the figure we know that AB || DC and AD || BC.

(iv) From the figure we know that PQ || TS, UT || QR and UP || SR.

(v) From the figure we know that AB || EF || CD, BC || AD and CF || DE.

(vi) From the figure we know that EF || BC, AB || DF and AC || DE.

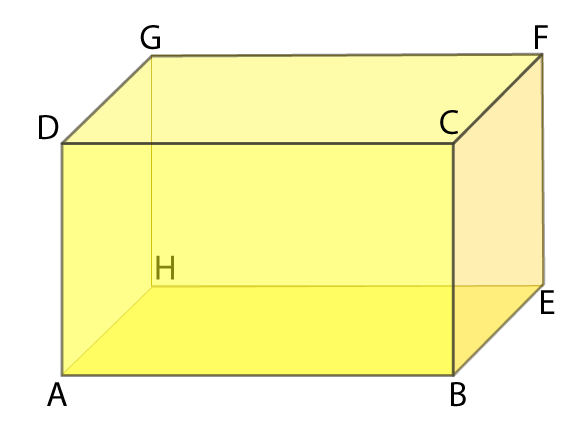
2. Name the pairs of all possible parallel edges of the pencil box whose figure is shown in Fig. 15.7.

Solution:

The pairs of all possible parallel edges of the pencil box are

AB || DC || HE || GF, AD || GH || BC || EF and AH || DG || BE || CF

3. In Fig. 15.8, do the segments AB and CD intersect? Are they parallel? Give reasons.

Solution:

No, AB and CD do not intersect but they can intersect if extended further. No AB and CD are not parallel since, the distance between them is not constant.

4. State which of the following statements are true (T) or which are false (F):

(i) If two lines in the same plane do not intersect, then they must be parallel.

(ii) Distance between two parallel lines is not same everywhere.

(iii) If m ⊥ l, n ⊥ l and m ≠ n, then m || n.

(iv) Two non-intersecting coplanar rays are parallel.

(v) If ray AB || line m, then line segment AB.

(vi) If line AB || line m, then line segment AB || m.

(vii) No two parallel line segments intersect.

(viii) Every pair of lines is a pair of coplanar lines.

(ix) Two lines perpendicular to the same line are parallel.

(x) A line perpendicular to one of two parallel lines is perpendicular to the other.

Solution:

(i) True

(ii) False

(iii) True

(iv) False

(v) True

(vi) True

(vii) True

(viii) False

(ix) True

(x) True

Exercise 15.2 page: 15.6

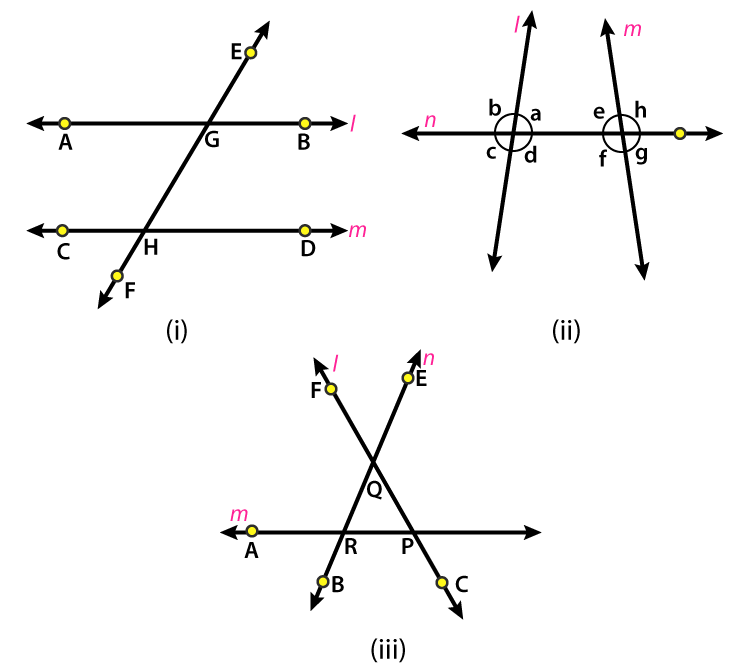
1. In Fig. 15.17, line n is a transversal to lines l and m. Identify the following:

(i) Alternate and corresponding angles in Fig. 15.17 (i).

(ii) Angles alternate to ∠d and ∠g and angles corresponding to ∠f and ∠h in Fig. 15.17 (ii).

(iii) Angle alternative to ∠PQR, angle corresponding to ∠RQF and angle alternate to ∠PQE in Fig. 15.17 (iii).

(iv) Pairs of interior and exterior angles on the same side of the transversal in Fig. 15.17 (ii).

Solution:

(i) Alternate interior angles are ∠BGH and ∠CHG; ∠AGH and ∠CHF

Alternate exterior angles are ∠AGE and ∠DHF; ∠EGB and ∠CHF

Corresponding angles are ∠EGB and ∠GHD; ∠EGA and ∠GHC; ∠BGH and ∠DHF; ∠AGF and ∠CHF.

(ii) Angles alternate to ∠d and ∠g are ∠e and ∠b and angles corresponding to ∠f and ∠h are ∠c and ∠a.

(iii) From the figure we know that l is transversal to m and n.

Angle alternate to ∠PQR is ∠QRA

Angle corresponding to ∠RQF is ∠BRA

Angle alternate to ∠PQE is ∠BRA

(iv) Interior angles are ∠d, ∠f and ∠a, ∠e and exterior angles are ∠c, ∠g and ∠b, ∠h

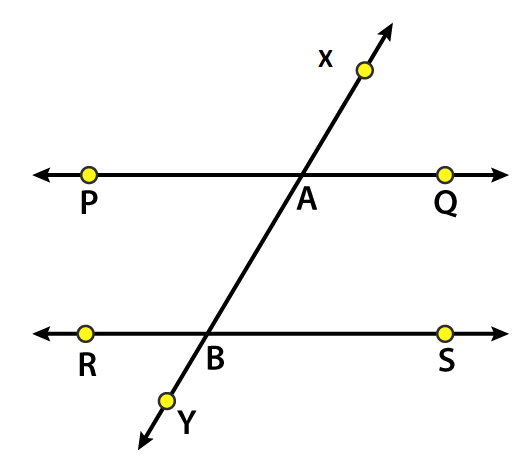
2. Match column A and column B with the help of the Fig. 15.18:

Column A Column B

(i) Vertically opposite angles (i) ∠PAB and ∠ABS

(ii) Alternate angles (ii) ∠PAB and ∠RBY

(iii) Corresponding angles (iii) ∠PAB and ∠XAQ

Solution:

(i) ∠PAB and ∠XAQ are vertically opposite angles

(ii) ∠PAB and ∠ABS are alternate angles

(iii) ∠PAB and ∠RBY are corresponding angles

RD Sharma Solutions for Class 6 Maths Chapter 15: Download PDF

RD Sharma Solutions for Class 6 Maths Chapter 15–Pair of Lines and Transversal

Download PDF: RD Sharma Solutions for Class 6 Maths Chapter 15–Pair of Lines and Transversal PDF

Chapterwise RD Sharma Solutions for Class 6 Maths :

About RD Sharma

RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.

R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.

Read More