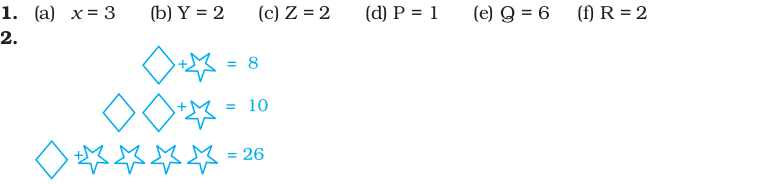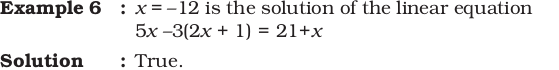NCERT Exemplar Class 8 Maths Chapter 4: Linear Equations in One Variable. NCERT Exemplar Solutions for Class 8 Maths Chapter 4 Linear Equations in One Variable prepare students for their Class 8 exams thoroughly.
Maths problems and solutions for the Class 8 pdf are provided here which are similar to the questions being asked in the previous year’s board.
Contents
- 1 NCERT Exemplar Class 8 Maths Chapter 4: Linear Equations in One Variable
- 1.1 Main Concepts and Results
- 1.2 Solved Examples
- 1.3 In examples 3 and 4, fill in the blanks to make the statements true.
- 1.4 You have to Keep Equations Balanced
- 1.5
- 1.6 In examples 7 to 10 solve each of them.
- 1.7
- 1.8
- 1.9
- 1.10
- 1.11
- 1.12
- 1.13
- 1.14 Check
- 1.15 Think and Discuss
- 1.16 Multiple Choice Questions
- 1.17 Applications, Games and Puzzles
- 1.18 Answers to Multiple Choice Questions
- 1.19 Applications, Games and Puzzles
NCERT Exemplar Class 8 Maths Chapter 4: Linear Equations in One Variable
Class 8: Maths Chapter 4 solutions. Complete Class 8 Maths Chapter 4 Notes.
Main Concepts and Results
- An algebraic equation is an equality involving variables. It has an equality sign. The expression on the left of the equality sign is the Left Hand Side (LHS) and the expression on the right of the equality sign is the Right Hand Side (RHS).
- In an equation the values of the expressions on the LHS and RHS are equal for certain values of the variables. These values are the solutions of the equation.
- Equations where the expressions which form the equation contain only one variable and the highest power of the variable appearing in the equation is 1, are called linear equations in one variable.
- A linear equation may have linear expressions on both sides of the equality sign.
- To find the solution of an equation we perform the same mathematical operations on both sides of the equation, so that the balance between the LHS and RHS is not disturbed.
- A linear equation may have any rational number as its solution.
- In an equation, variables can be transposed from one side of the equation to the other.
Solved Examples
In examples 1 and 2, there are four options given out of which one is
correct. Choose the correct answer.

In examples 3 and 4, fill in the blanks to make the statements true.

In examples 5 and 6, state whether the given statements are true (T) or false (F).
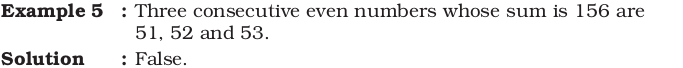
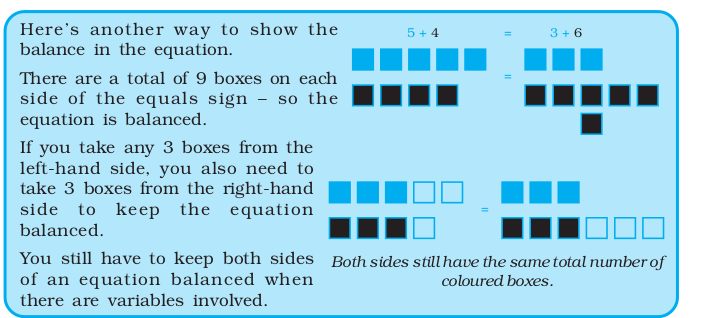
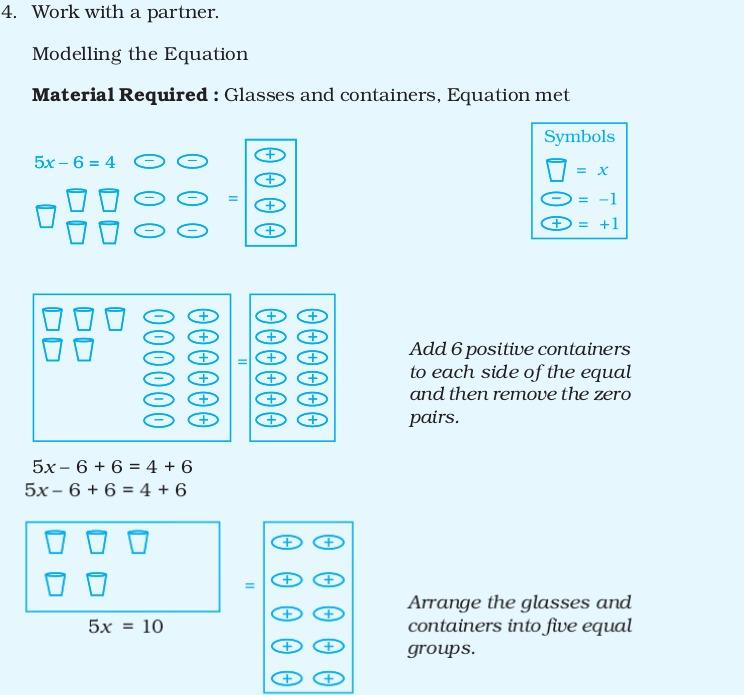
You have to Keep Equations Balanced
Main Concepts and Results
An algebraic equation is an equality involving variables. It has an equality sign. The expression on the left of the equality sign is the Left Hand Side (LHS) and the expression on the right of the equality sign is the Right Hand Side (RHS).
In an equation the values of the expressions on the LHS and RHS are equal for certain values of the variables. These values are the solutions of the equation.
Equations where the expressions which form the equation contain only one variable and the highest power of the variable appearing in the equation is 1, are called linear equations in one variable.
A linear equation may have linear expressions on both sides of the equality sign.
To find the solution of an equation we perform the same mathematical operations on both sides of the equation, so that the balance between the LHS and RHS is not disturbed.
A linear equation may have any rational number as its solution.
In an equation, variables can be transposed from one side of the equation to the other.
Solved Examples
In examples 1 and 2, there are four options given out of which one is
correct. Choose the correct answer.
In examples 3 and 4, fill in the blanks to make the statements true.
In examples 5 and 6, state whether the given statements are true (T) or false (F).
You have to Keep Equations Balanced
In examples 7 to 10 solve each of them.
Check
Verify your answer by adopting some other plan.
e.g. Here in this problem instead of taking perimeter as
sum of its sides, use the formula
4s = 6480 cm
s = 1620 cm
Hence verified.
Think and Discuss
What other values will be needed if instead of square it is a rectangular or circular garden?
What will happen if we have to level the grass inside it instead of fencing the garden?
What will happen if there is a path running inside it?
In examples 7 to 10 solve each of them.
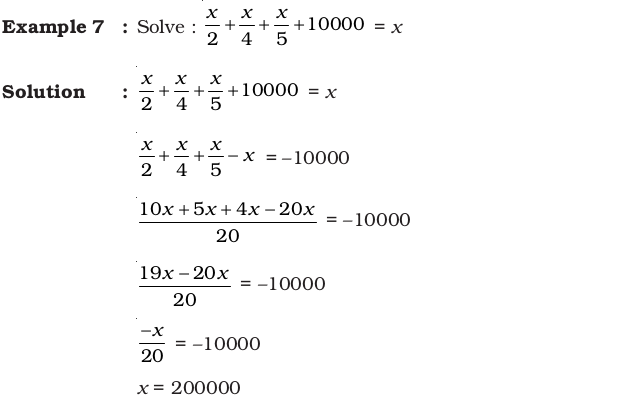
Check
Verify your answer by adopting some other plan.
e.g. Here in this problem instead of taking perimeter as
sum of its sides, use the formula
4s = 6480 cm
s = 1620 cm
Hence verified.
Think and Discuss
- What other values will be needed if instead of square it is a rectangular or circular garden?
- What will happen if we have to level the grass inside it instead of fencing the garden?
- What will happen if there is a path running inside it?
Multiple Choice Questions

Fill in the Blanks Type Questions

True False Type Questions

Short Answer Type Questions

Applications, Games and Puzzles


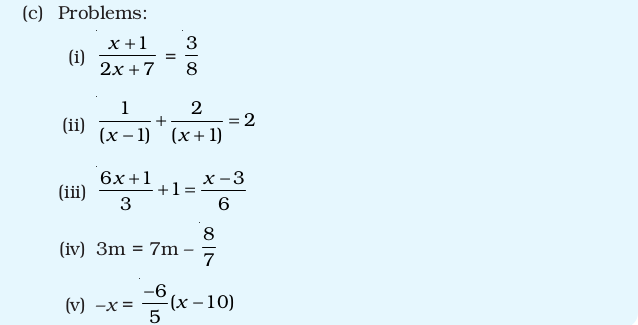


Answers to Multiple Choice Questions



Applications, Games and Puzzles