Maharashtra Board Solutions Class 9-Maths (Part 1): Chapter 5.1- Linear Equations in Two Variables
Maharashtra Board Solutions Class 9-Maths (Part 1): Chapter 5.1- Linear Equations in Two Variables

Class 9: Maths Chapter 5.1 solutions. Complete Class 9 Maths Chapter 5.1 Notes.

Maharashtra Board Solutions Class 9-Maths (Part 1): Chapter 5.1- Linear Equations in Two Variables

Maharashtra Board 9th Maths Chapter 5.1, Class 9 Maths Chapter 5.1 solutions

Question 1.
By using variables x and y form any five linear equations in two variables.
Answer:
The general form of a linear equation in two variables x and y is ax + by + c = 0,
where a, b, c are real numbers and a ≠ 0, b ≠ 0.
Five linear equations in two variables are as follows:
i. 3x + 4y – 12 = 0
ii. 3x – 4y + 12 = 0
iii. 5x + 5y – 6 = 0
iv. 7x + 12y – 11 = 0
v. x – y + 5 = 0

Question 2.
Write five solutions of the equation x + y = 1.
Answer:
i. x = 1, y = 6
ii. x = -1, y = 8
iii. x = 5, y = 2
iv. x = 0, y = 7
v. x = 10, y = -3

Question 3.
Solve the following sets of simultaneous equations.
i. x + y = 4 ; 2x – 5y = 1
ii. 2x + y = 5 ; 3x – y = 5
iii. 3x – 5y = 16; x – 3y= 8
iv. 2y – x = 0; 10x + 15y = 105
v. 2x + 3y + 4 = 0; x – 5y = 11
vi. 2x – 7y = 7; 3x + y = 22
Solution:
i. Substitution Method:
x + y = 4
∴ x = 4 – y …(i)
2x – 5y = 1 ……(ii)
Substituting x = 4 – y in equation (ii),
2(4 – y) – 5y = 1
∴ 8 – 2y – 5y = 1
∴ 8 – 7y = 1
∴ 8 – 1 = 7y
∴ 7 = 7y
∴ y = 77
∴ y = 1
Substituting y = 1 in equation (i),
x = 4 – 1 = 3
∴ (3,1) is the solution of the given equations.

Alternate method:
Elimination Method:
x + y = 4 …(i)
2x – 5y = 1 ……(ii)
Multiplying equation (i) by 5,
5x + 5y = 20 … (iii)
Adding equations (ii) and (iii),
2x – 5y = 1
+ 5x + 5y = 20
7 = 21
∴ x = 217
∴ x = 3
Substituting x = 3 in equation (i),
3 + y = 4
∴ y = 4 – 3 = 1
(3,1) is the solution of the given equations.

ii. 2x + y = 5 …(i)
3x – y = 5 …(ii)
Adding equations (i) and (ii),
2x + y = 5
+ 3x – y = 5
5x = 10
∴ x = 105
∴ x = 2
Substituting x = 2 in equation (i),
2(2) + y = 5
4 + y = 5
∴ y = 5 – 4 = 1
∴ (2, 1) is the solution of the given equations.

iii. 3x – 5y = 16 …(i)
x – 3y = 8
∴x = 8 + 3y …..(ii)
Substituting x = 8 + 3y in equation (i),
3(8 + 3y) – 5y = 16
24 + 9y- 5y = 16
∴4y= 16 – 24
∴ 4y = -8
∴ y = −84
y = -2
Substituting y = -2 in equation (ii),
x = 8 + 3 (-2)
∴ x = 8 – 6 = 2
∴ (2, -2) is the solution of the given equations.

iv. 2y – x = 0
∴ x = 2y …(i)
10x + 15y = 105 …(ii)
Substituting x = 2y in equation (ii),
10(2y) + 15y = 105
∴ 20y + 15y = 105
∴ 35y = 105
∴ y = 10535
∴ y = 3
Substituting y = 3 in equation (i),
x = 2y
∴ x = 2(3) = 6
∴ (6, 3) is the solution of the given equations.

v. 2x + 3y + 4 = 0 …(i)
x – 5y = 11
∴x = 11 + 5y …(ii)
Substituting x = 11 + 5y in equation (i),
2(11 +5y) + 3y + 4 = 0
∴ 22 + 10y + 3y + 4 = 0
∴ 13y + 26 = 0
∴ 13y = -26
∴y = −2613
∴ y = -2
Substituting y = -2 in equation (ii),
x = 11 + 5y
∴ x = 11 + 5(-2)
∴ x = 11 – 10 = 1
∴ (1, -2) is the solution of the given equations.

vi. 2x – 7y = 7 …(i)
3x + y = 22
∴ y = 22 – 3x ……(ii)
Substituting y = 22 – 3x in equation (i),
2x – 7(22 – 3x) = 7
∴ 2x – 154 + 21x = 7
∴ 23x = 7 + 154
∴ 23x = 161
∴ x = 16123
∴ x = 7
Substituting x = 7 in equation (ii),
y = 22 – 3x
∴ y = 22 – 3(7)
∴ 7 = 22 -21= 1
∴ (7, 1) is the solution of the given equations.

Question 1.
Solve the following equations. (Textbook pg. no. 80)
i. m + 3 = 5
ii. 3y + 8 = 22
iii. x3 = 2
iv. 2p = p + 49
Solution:
i. m + 3 = 5
m = 5 – 3
∴m = 2

ii. 3y + 8 = 22
∴ 3y = 22 – 8
∴ 3y = 14
∴ y = 149

iii. x3 = 2
∴ x = 2 × 3
∴ x = 6

iv. 2p = p + 49
∴ 2p – p = 49
∴ p = 49

Question 2.
Which number should be added to 5 to obtain 14? (Textbook pg. no. 80)
Solution:
x + 5 = 14
∴ x = 14 – 5
x = 9
∴ 9 + 5 = 14

Question 3.
Which number should be subtracted from 8 to obtain 2? (Textbook pg. no. 80)
Solution:
8 – y = 2
∴ y = 8 – 2
∴ y = 6
∴ 8 – 6 = 2

Question 4.
x + y = 5 and 2x + 2y= 10 are two equations in two variables. Find live different solutions of x + y = 5, verify whether same solutions satisfy the equation 2x + 2y = 10 also. Observe both equations. Find the condition where two equations in two variables have all solutions in common. (Textbook pg. no. 82)
Solution:
Five solutions of x + y = 5 are given below:
(1,4), (2, 3), (3, 2), (4,1), (0, 5)
The above solutions also satisfy the equation 2x + 2y = 10.
∴ x + y = 5 …[Dividing both sides by 2]
∴ If the two equations are the same, then the two equations in two variables have all solutions common.

Question 5.
3x – 4y – 15 = 0 and y + x + 2 = 0. Can these equations be solved by eliminating x ? Is the solution same? (Textbook pg. no. 84)
Solution:
3x – 4y – 15 = 0
∴ 3x – 4y = 15 …(i)
y + x + 2 = 0
∴ x + y = -2 ……(ii)
Multiplying equation (ii) by 3,
3x + 3y = -6 …(iii)
Subtracting equation (iii) from (i),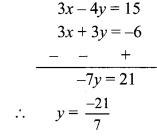
Maharashtra Board Class 9 Maths Solutions Chapter 5 Linear Equations in Two Variables Practice Set 5.1 1
∴ y = -3
Substituting y = -3 in equation (ii),
∴ x – 3 = -2
∴ x = – 2 + 3
∴ x = 1
∴ (x, y) = ( 1, -3)
Yes, the given equations can be solved by eliminating x. Also, the solution will remain the same.

Download PDF

Maharashtra Board Solutions Class 9-Maths (Part 1): Chapter 5.1- Linear Equations in Two Variables

Download PDF: Maharashtra Board Solutions Class 9-Maths (Part 1): Chapter 5.1- Linear Equations in Two Variables PDF

Chapterwise Maharashtra Board Solutions Class 9 Maths :

Part 1

FAQs

Where do I get the Maharashtra State Board Books PDF For free download?

You can download the Maharashtra State Board Books from the eBalbharti official website, i.e. cart.ebalbharati.in or from this article.

How to Download Maharashtra State Board Books?

Students can get the Maharashtra Books for primary, secondary, and senior secondary classes from here.  You can view or download the Maharashtra State Board Books from this page or from the official website for free of cost. Students can follow the detailed steps below to visit the official website and download the e-books for all subjects or a specific subject in different mediums.
Step 1: Visit the official website ebalbharati.in
Step 2: On the top of the screen, select “Download PDF textbooks” 
Step 3: From the “Classes” section, select your class.
Step 4: From “Medium”, select the medium suitable to you.
Step 5: All Maharashtra board books for your class will now be displayed on the right side. 
Step 6: Click on the “Download” option to download the PDF book.

Who developed the Maharashtra State board books?

As of now, the MSCERT and Balbharti are responsible for the syllabus and textbooks of Classes 1 to 8, while Classes 9 and 10 are under the Maharashtra State Board of Secondary and Higher Secondary Education (MSBSHSE).

How many state boards are there in Maharashtra?

The Maharashtra State Board of Secondary & Higher Secondary Education, conducts the HSC and SSC Examinations in the state of Maharashtra through its nine Divisional Boards located at Pune, Mumbai, Aurangabad, Nasik, Kolhapur, Amravati, Latur, Nagpur and Ratnagiri.

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC. 

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.