Maharashtra Board for Class 9, Maths Chapter 1.4

Class 9: Maths Chapter 1.4 solutions. Complete Class 9 Maths Chapter 1.4 Notes.

Contents

1 Maharashtra Board Solutions Class 9-Maths (Part 1): Chapter 1.4- Sets
2 Download PDF
3 Chapterwise Maharashtra Board Solutions Class 9 Maths :
4 FAQs
5 About Maharashtra State Board (MSBSHSE)

Maharashtra Board Solutions Class 9-Maths (Part 1): Chapter 1.4- Sets

Maharashtra Board 9th Maths Chapter 1.4, Class 9 Maths Chapter 1.4 solutions

Question 1.
If n(A) = 15, n(A ∪ B) = 29, n(A ∩ B) = 7, then n(B) = ?
Solution:
Here, n(A) = 15, n(A ∪ B) = 29, n(A ∩ B) = 7
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ 29 = 15 + n(B) – 7
∴ 29 – 15 + 7 = n(B)
∴ n(B) = 21

Question 2.
In a hostel there are 125 students, out of which 80 drink tea, 60 drink coffee and 20 drink tea and coffee both. Find the number of students who do not drink tea or coffee.
Solution:
i. Let U be the set of students in the hostel, T be the set of students who drink tea and C be the set of students who drink coffee.
n(U) = 125, n(T) = 80, n(C) = 60,
number of students who drink Tea and Coffee = n(T ∩ C) = 20

ii. n(T ∪ C) = n(T) + n(C) – n(T ∩ C)
= 80 + 60 – 20
∴ n(T ∪ C) = 120
∴ 120 students drink tea or coffee
Also, there are 125 students in the hostel.

iii. Number of students who do not drink tea or coffee = n(U) – n(T ∪ C)
= 125 – 120
= 5
∴ 5 students do not drink tea or coffee.

Alternate Method:
Let U be the set of students in the hostel, T be the set of students who drink tea and C be the set of students who drink coffee.

From Venn diagram,
Student who drinks tea or coffee = n(T ∪ C) = 60 + 20 + 40 = 120
∴ The number of students who do not drink tea or coffee = n(U) – n(T ∪ C)
= 125 – 120 = 5
∴ 5 students do not drink tea or coffee.

Question 3.
In a competitive exam 50 students passed in English, 60 students passed in Mathematics and 40 students passed in both the subjects. None of them failed in both the subjects. Find the number of students who passed at least in one of the subjects ?
Solution:
Let U be the set of students who appeared for the exam,
E be the set of students who passed in English and
M be the set of students who passed in Maths.
∴ n(E) = 50, n(M) = 60,
40 students passed in both the subjects
∴ n(M ∩ E) = 40
Since, none of the students failed in both subjects
∴ Total students = n(E ∪M)
= n(E) + n(M) – n(E ∩ M)
= 50 + 60 – 40
= 70
∴ The number of students who passed at least in one of the subjects is 70.

Alternate Method:
Let U be the set of students who appeared for the exam,
E be the set of students who passed in English and M be the set of students who passed in Maths.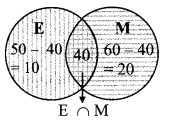

Since, none of the students failed in both subjects
∴ Total student = n(E ∪M)
= 10 + 40 + 20
= 70
∴ The number of students who passed at least in one of the subjects is 70.

Question 4.
A survey was conducted to know the hobby of 220 students of class IX. Out of which 130 students informed about their hobby as ’rock climbing and 180 students informed about their hobby as sky watching. There are 110 students who follow both the hobbies. Then how many students do not have any of the two hobbies? How many of them follow the hobby of rock climbing only? How many students follow the hobby of sky watching only?
Solution:
i. Let U be the set of students of class IX,
R be the set of students who follow the hobby of rock climbing and
S be the set of students who follow the hobby of sky watching.
∴ n (U) = 220, n (R) = 130, n (S) = 180,
110 students follow both the hobbies
∴ n (R ∩ S) = 110

ii. n(R ∪ S)=n (R) + n (S) – n (R ∩ S)
= 130 + 180 – 110
∴n (R ∪ S) = 200
∴ 200 students follow the hobby of rock climbing or sky watching.

iii. Total number of students = 220.
Number of students who do not follow the hobby of rock climbing or sky watching
= n (U) – n (R ∪ S)
= 220 – 200
= 20

iv. Number of students who follow the hobby of rock climbing only
= n (R) – n(R ∩ S)
= 130 – 110
= 20

v. Number of students who follow the hobby of sky watching only
= n (S) – n (R ∩ S)
= 180 – 110
= 70

Alternate Method:
Let U be the set of students of class IX,
R be the set of students who follow the hobby of rock climbing and
S be the set of students who follow the hobby of sky watching.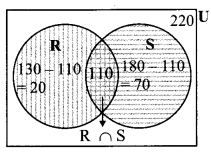

From the Venn diagram
i. Students who follow the hobby of rock climbing or sky watching
= n(R ∪ S)
= 20 + 110 + 70
= 200

ii. Number of students who do not follow the hobby of rock climbing or sky watching
= n (U) – n(R ∪S)
= 220 – 200
= 20

iii. Number of students who follow the hobby of rock climbing only
= n (R) – n(R ∩S)
= 130 – 110
= 20

iv. Number of students who follow the hobby of sky watching only
= n (S) – n (R ∩ S)
= 180 – 110
= 70

Question 5.
Observe the given Venn diagram and write the following sets.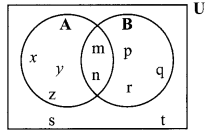

i. A
ii. B
iii. A ∪ B
iv. U
v. A’
vi. B’
vii. (A ∪B )’
Ans:
i. A = {x, y, z, m, n}
ii. B = {p, q, r, m, n}
iii. A ∪ B = {x, y, z, m, n, p, q, r }
iv. U = {x, y, z, m, n, p, q, r, s, t}
v. A’ = {p, q, r, s, t}
vi. B’ = {x, y, z, s, t}
vii. (A ∪ B )’ = {s, t}

Question 1.
Take different examples of sets and verify the above mentioned properties. (Textbook pg.no. 12)
Solution:
i. Let A = {3, 5}, B= {3, 5, 8, 9, 10}
A ∩ B = B ∩ A = {3, 5}

ii. Let A = {3, 5}, B = {3, 5, 8, 9, 10}
Since, all elements of set A are present in set B.
∴ A ⊆ B
Also, A ∩ B = {3, 5} = A
∴ If A ⊆ B, then A ∩B = A.

iii. Let A = {2, 3, 8, 10}, B = {3,8}
A ∩ B = {3, 8} = B
Also, all the elements of set B are present in set A
∴ B ⊆ A
∴ If A ∩ B = B, then B ⊆ A.

iv. Let A = {2, 3, 8, 10}, B = {3, 8}, A ∩B = {3, 8}
Since, all the elements of set A n B are present in set A and B
A ∩ B ⊆ A and A ∩B ⊆B

v. Let U= {3, 4, 6, 8}, A = {6, 4}
∴ A’ = {3, 8}
∴ A ∩ A’= { } = φ

vi. A ∩ φ = { } = φ

vii. Let A = {6, 4}
∴ A ∩ A = {6, 4}
∴ A ∩ A = A

Question 2.
Observe the set A, B, C given by Venn diagrams and write which of these are disjoint sets. (Textbook pg. no. 12)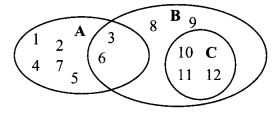

Solution:
Here, A = {1, 2, 3, 4, 5, 6, 7}
B = {3, 6, 8, 9, 10, 11, 12}
C = {10, 11, 12}
Now, A ∩ C = φ
∴ A and C are disjoint sets.

Question 3.
Let the set of English alphabets be the Universal set. The letters of the word ‘LAUGH’ is one set and the letter of the word ‘CRY’ is another set. Can we say that these are two disjoint sets? Observe that intersection of these two sets is empty. (Textbook pg. no. 13)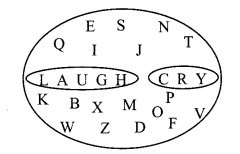

Solution:
Let A = {L, A, U, G, H}
B = {C, R, Y}
Now, A ∩ B = φ
∴ A and B are disjoint sets.

Question 4.
Fill in the blanks with elements of that set.
U = {1, 3, 5, 8, 9, 10, 11, 12, 13, 15}
A = {1,11, 13}
B = {8,5, 10, 11, 15}
A’ = { }
B’ = { }
A ∩ B = { }
A’ ∩ B’ = { }
A ∪ B = { }
A’ ∪ B’= { }
(A ∩ B)’ = { }
(A ∪ B)’ = { }
Verify: (A ∩ B)’ = A’ u B’, (A u B)’ = A’ ∩ B’ (Textbook pg. no, 18)
Solution:
U = {1, 3, 5, 8, 9, 10, 11, 12, 13, 15}
A = {1, 11, 13}
B = {8, 5, 10, 11, 15}
A’ = {3, 5, 8, 9, 10, 12, 15}
B’ = {1, 3, 9, 12, 13}
A∩ B= {11}
A’ ∩ B’= {3, 9, 12} …(i)
A ∪ B = {1, 5, 8, 10, 11, 13, 15}
A’ ∪ B’ = { 1, 3, 5, 8, 9, 10, 12, 13, 15} …(ii)
(A ∩ B)’= { 1, 3, 5, 8, 9, 10, 12, 13,15} …(iii)
(A ∪ B)’ = {3, 9, 12} ,..(iv)
(A ∩ B)’ = A’ ∪ B’ … [From (ii) and (iii)]
(A ∪ B)’ = A’ ∩ B’ … [From (i) and (iv)]

Question 5.
A = {1,2,3, 5, 7,9,11,13}
B = {1,2,4, 6, 8,12,13}
Verify the above rule for the given set A and set B. (Textbook pg. no. 14)
Solution:
A = {1, 2, 3, 5, 7, 9, 11, 13}
B = {1, 2, 4, 6, 8, 12, 13}
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13}
A ∩ B= {1, 2, 13}
n(A) = 8, n(B) = 7,
n(A ∪ B) = 12, n(A ∩ B) = 3
n(A ∩ B) = 12 …(i)
n(A) + n(B) – n(A ∩ B) = 8 + 7 – 3 = 12 …(ii)
∴ n(A ∪ B) = n(A) + n(B) – n(A ∩ B) … [From (i) and (ii)]

Question 6.
Verify the above rule for the given Venn diagram. (Textbook pg. no. 14)

Solution:
n(A) = 5 , n(B) = 6
n(A ∪ B) = 9 , n(A ∩ B) = 2
Now, n(A ∪ B) = 9 …(i)
n(A) + n(B) – n(A ∩ B) = 5 + 6 – 2 = 9 …(ii)
∴ n(A ∪ B) = n(A) + n(B) – n(A ∩ B). …[From (i) and (ii)]

Download PDF

Maharashtra Board Solutions Class 9-Maths (Part 1): Chapter 1.4- Sets

Download PDF: Maharashtra Board Solutions Class 9-Maths (Part 1): Chapter 1.4- Sets PDF

Chapterwise Maharashtra Board Solutions Class 9 Maths :

Part 1

FAQs

Where do I get the Maharashtra State Board Books PDF For free download?

You can download the Maharashtra State Board Books from the eBalbharti official website, i.e. cart.ebalbharati.in or from this article.

How to Download Maharashtra State Board Books?

Students can get the Maharashtra Books for primary, secondary, and senior secondary classes from here. You can view or download the Maharashtra State Board Books from this page or from the official website for free of cost. Students can follow the detailed steps below to visit the official website and download the e-books for all subjects or a specific subject in different mediums.
Step 1: Visit the official website ebalbharati.in
Step 2: On the top of the screen, select “Download PDF textbooks”
Step 3: From the “Classes” section, select your class.
Step 4: From “Medium”, select the medium suitable to you.
Step 5: All Maharashtra board books for your class will now be displayed on the right side.
Step 6: Click on the “Download” option to download the PDF book.

Who developed the Maharashtra State board books?

As of now, the MSCERT and Balbharti are responsible for the syllabus and textbooks of Classes 1 to 8, while Classes 9 and 10 are under the Maharashtra State Board of Secondary and Higher Secondary Education (MSBSHSE).

How many state boards are there in Maharashtra?

The Maharashtra State Board of Secondary & Higher Secondary Education, conducts the HSC and SSC Examinations in the state of Maharashtra through its nine Divisional Boards located at Pune, Mumbai, Aurangabad, Nasik, Kolhapur, Amravati, Latur, Nagpur and Ratnagiri.

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC.

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.