Maharashtra Board Solutions Class 12-Arts & Science Maths (Part 1): Chapter 7- Linear Programming

Class 12: Maths Chapter 7 solutions. Complete Class 12 Maths Chapter 7 Notes.

Maharashtra Board Solutions Class 12-Arts & Science Maths (Part 1): Chapter 7- Linear Programming

Maharashtra Board 12th Maths Chapter 7, Class 12 Maths Chapter 7 solutions

Ex 7.1

Question 1.
Solve graphically :
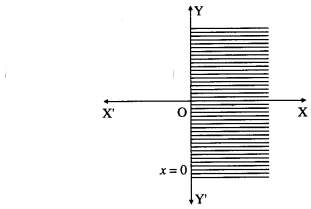
(i) x ≥ 0
Solution:
Consider the line whose equation is x = 0. This represents the Y-axis.
To find the solution set, we have to check any point other than origin.
Let us check the point (1, 1)
When x = 1, x ≥ 0
∴ (1, 1) lies in the required region
Therefore, the solution set is the Y-axis and the right
side of the Y-axis which is shaded in the graph.

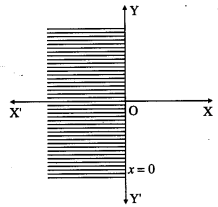
ii) x ≤ 0
Solution:
Consider the line whose equation is x = 0.
This represents the Y-axis.
To find the solution set, we have to check any point other than origin.
Let us check the point (1, 1).
When x = 1, x ≰ 0
∴ (1, 1) does not lie in the required region.
Therefore, the solution set is the Y-axis and the left side of the Y-axis which is shaded in the graph.

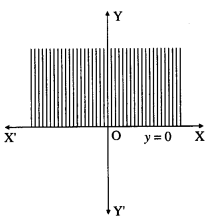
(iii) y ≥ 0
Solution:
Consider the line whose equation is y = 0. This represents the X-axis. To find the solution set, we have to check any point other than origin. Let us check the point (1, 1).
When y = 1, y ≥ 0
∴ (1, 1) lies in the required region.
Therefore, the solution set is the X-axis and above the X-axis which is shaded in the graph.

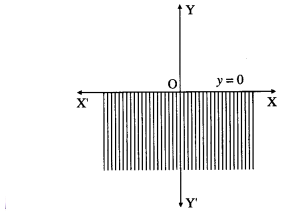
(iv) y ≤ 0
Solution:
(iv) Consider the line whose equation is y = 0. This represents the X-axis.
To find the solution set, we have to check any point other than origin.
Let us check the point (1, 1).
When y = 1, y ≰ 0.
∴ (1, 1) does not lie in the required region.
Therefore, the solution set is the X-axis and below the X-axis which is shaded in the graph.

Question 2.
Solve graphically :
(i) x ≥ 0 and y ≥ 0
Solution:
Consider the lines whose equations are x = 0, y = 0.
These represents the equations of Y-axis and X-axis respectively, which divide the plane into four parts.
(i) Since x ≥ 0, y ≥ 0, the solution set is in the first quadrant which is shaded in the graph.

(ii) x ≤ 0 and y ≥ 0
Solution:
Since x ≤ 0, y ≥ 0, the solution set is in the second quadrant which is shaded in the graph.

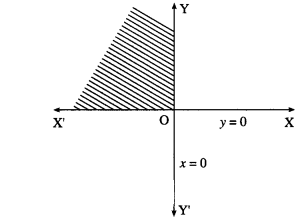
(iii) x ≤ 0 and y ≤ 0
Solution:
Since x ≤ 0, y ≤ 0, the solution set is in the third quadrant which is shaded in the graph.

(iv) x ≥ 0 and y ≤ 0
Solution:
Since x ≥ 0, y ≤ 0, the solution set is in the fourth ! quadrant which is shaded in the graph.

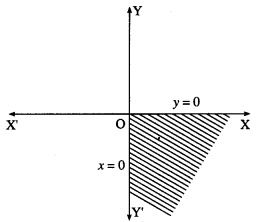
Question 3.
Solve graphically :
(i) 2x – 3 ≥ 0
Solution:

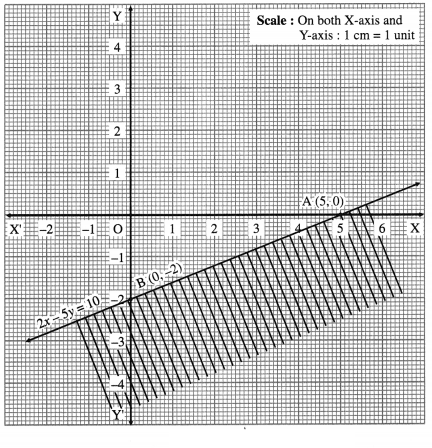
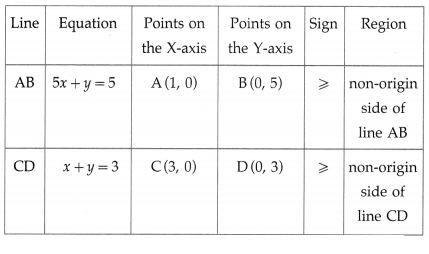
Draw the line AB joining these points. This line J divide the plane in two parts.
1. Origin side 2. Non-origin side
To find the solution set, we have to check the position of the origin (0, 0) with respect to the line. When x = 0, y = 0, then 2x – 5y = 0 which is neither greater nor equal to 10.
∴ 2x – 5y ≱ 10 in this case.
Hence (0, 0) will not lie in the required region.
Therefore, the given inequality is the non-origin side, which is shaded in the graph.
This is the solution set of 2x – 5y ≥ 10.

(iii) 3x + 2y ≥ 0
Solution:
Consider the line whose equation is 3x + 2y = 0.
The constant term is zero, therefore this line is passing through the origin.
∴ one point on the line is O ≡ (0, 0).
To find the another point, we can give any value of x and get the corresponding value of y.
Put x = 2, we get 6 + 2y = 0 i.e. y = – 3
∴ A = (2, -3) is another point on the line.
Draw the line OA.
To find the solution set, we cannot check (0, 0) as it is already on the line.
We can check any other point which is not on the line.
Let us check the point (1, 1)

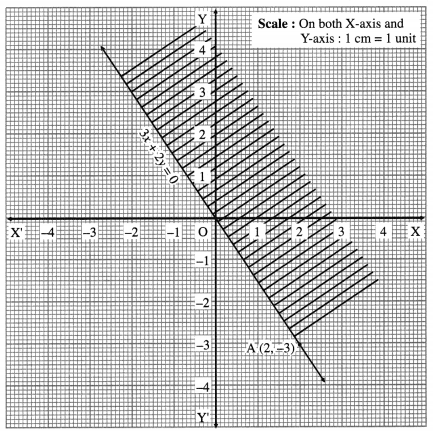
When x = 1, y = 1, then 3x + 2y = 3 + 2 = 5 which is greater than zero.
∴ 3x + 2y > 0 in this case.
Hence (1, 1) lies in the required region. Therefore, the required region is the upper side which is shaded in the graph.
This is the solution set of 3x + 2y ≥ 0.

(iv) 5x – 3y ≤ 0
Solution:
Consider the line whose equation is 5x – 3y = 0. The constant term is zero, therefore this line is passing through the origin.
∴ one point on the line is the origin O = (0, 0).
To find the other point, we can give any value of x and get the corresponding value of y.
Put x = 3, we get 15 – 3y = 0, i.e. y = 5
∴ A ≡ (3, 5) is another point on the line.
Draw the line OA.
To find the solution set, we cannot check 0(0, 0), as it is already on the line. We can check any other point which is not on the line.
Let us check the point (1, -1).
When x = 1, y = -1 then 5x – 3y = 5 + 3 = 8
which is neither less nor equal to zero.
∴ 5x – 3y ≰ 0 in this case.
Hence (1, -1) will not lie in the required region. Therefore, the required region is the upper side which is shaded in the graph.

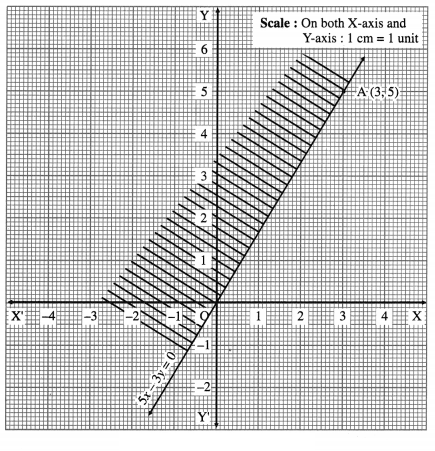
This is the solution set of 5x – 3y ≤ 0.

Question 5.
Solve graphically :
(i) 2x + y ≥ 2 and x – y ≤ 1
Solution:
First we draw the lines AB and AC whose equations are 2x + y = 2 and x – y = 1 respectively.

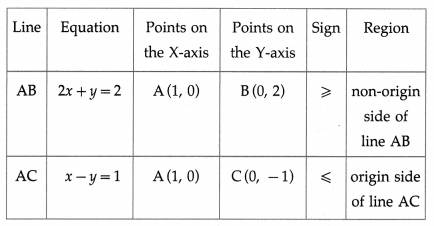
The solution set of the given system of inequalities is shaded in the graph.

(ii) x – y ≤ 2 and x + 2y ≤ 8
Solution:
First we draw the lines AB and CD whose equations are x – y = 2 and x + 2y = 8 respectively.

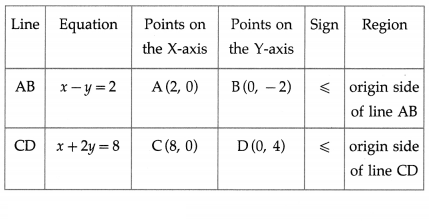
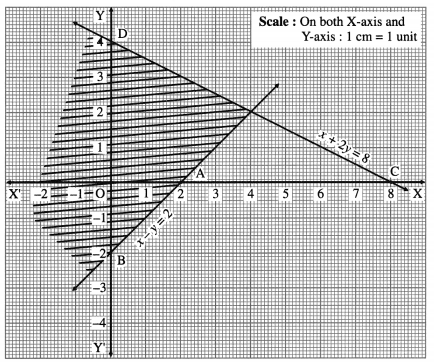
The solution set of the given system of inequalities is shaded in the graph.

(iii) x + y ≥ 6 and x + 2y ≤ 10
Solution:
First we draw the lines AB and CD whose equations are x + y = 6 and x + 2y = 10 respectively.

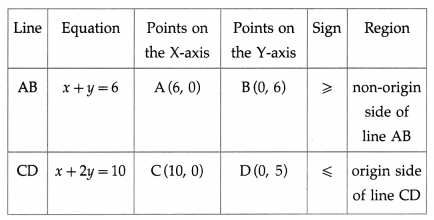
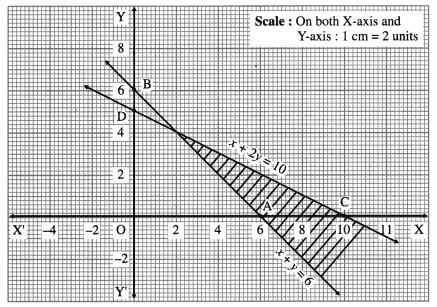
The solution set of the given system of inequalities is shaded in the graph.

(iv) 2x + 3y ≤ 6 and x + 4y ≥ 4
Solution:
First we draw the lines AB and CD whose equations are 2x + 3y = 6 and x + 4y = 4 respectively.

The solution set of the given system of inequalities is shaded in the graph.

(v) 2x + y ≥ 5 and x – y ≤ 1
Solution:
First we draw the lines AB and CD whose equations are 2x + y = 5 and x – y = 1 respectively.

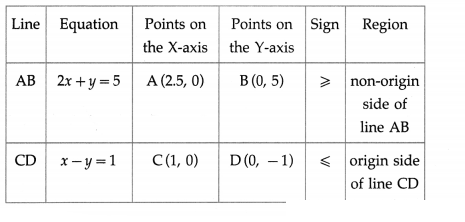
The solution set of the given system of inequations is shaded in the graph.

Ex 7.2

I) Find the feasible solution of the following inequations graphically.
Question 1.
3x + 2y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB and CD whose equations are 3x + 2y = 18 and 2x + y = 10 respectively.

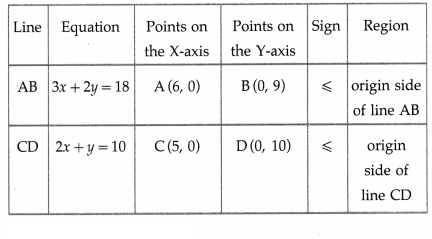
The feasible solution is OCPBO which is shaded in the graph.

Question 2.
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB and CB whose equations are 2x + 3y = 6 and x + y = 2 respectively.

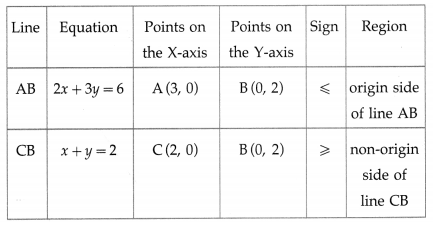
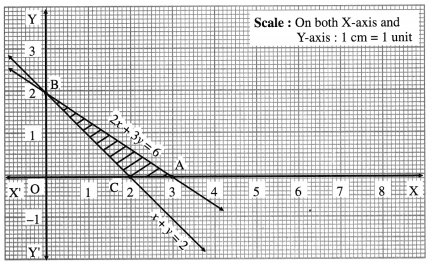
The feasible solution is ∆ABC which is shaded in the graph.

Question 3.
3x + 4y ≥ 12, 4x + 7y ≤ 28, y ≥ 1, x ≥ 0
Solution:
First we draw the lines AB, CD and EF whose equations are 3x + 4 y = 12, 4x + 7y = 28 and y = 1 respectively.

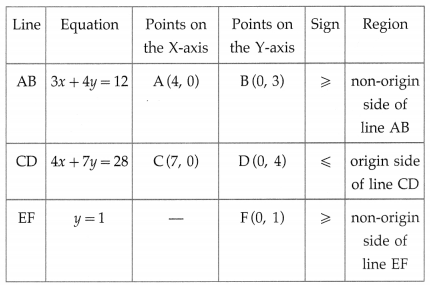
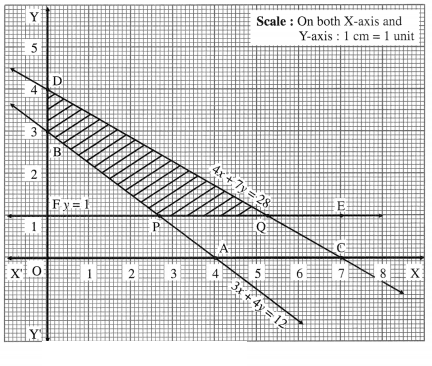
The feasible solution is PQDBP. which is shaded in the graph.

Question 4.
x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and EF whose equations are x + 4y = 24, 3x + y = 21 and x + y = 9 respectively.

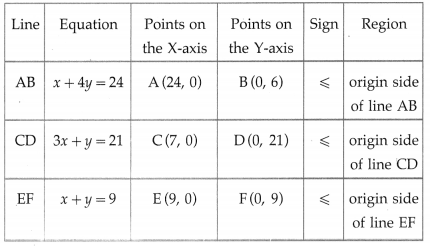
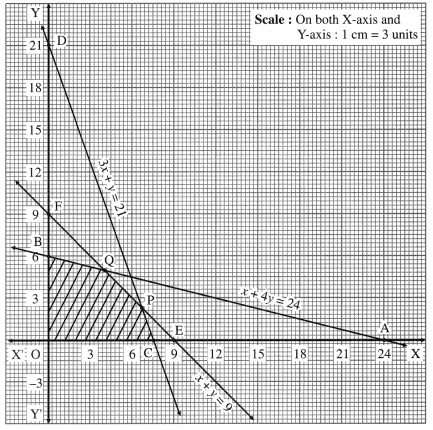
The feasible solution is OCPQBO. which is shaded in the graph.

Question 5.
0 ≤ x ≤ 3, 0 ≤ y ≤ 3, x + y ≤ 5, 2x + y ≥ 4
Solution:
First we draw the lines AB, CD, EF and GH whose equations are x + y = 5, 2x + y = 4, x = 3 and y = 3 respectively.

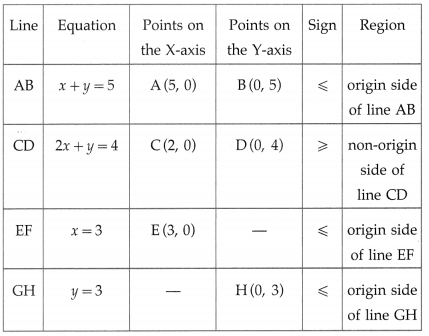
The feasible solution is CEPQRC. which is shaded in the graph.

Question 6.
x – 2y ≤ 2, x + y ≥ 3, -2x + y ≤ 4, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB, CD and EF whose equations are x – 2y = 2, x + y = 3 and -2x + y = 4 respectively.

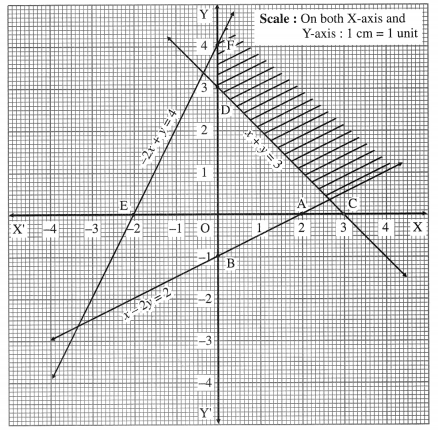
The feasible solution is shaded in the graph.

Question 7.
A company produces two types of articles A and B which requires silver and gold. Each unit of A requires 3 gm of silver and 1 gm of gold, while each unit of B requires 2 gm of silver and 2 gm of gold. The company has 6 gm of silver and 4 gm of gold. Construct the inequations and find the feasible solution graphically.
Solution:
Let the company produces x units of article A and y units of article B.
The given data can be tabulated as:

Inequations are :
x + 2y ≤ 4 and 3x + 2y ≤ 6
x and y are number of items, x ≥ 0, y ≥ 0
First we draw the lines AB and CD whose equations are x + 2y = 4 and 3x + 2y = 6 respectively.

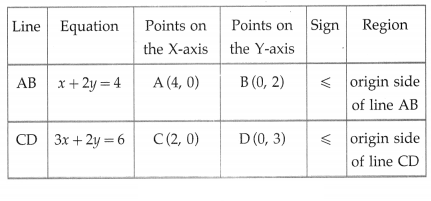
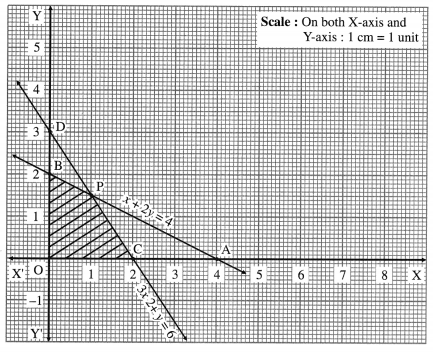
The feasible solution is OCPBO. which is shaded in the graph.

Question 8.
A furniture dealer deals in tables and chairs. He has Rs.1,50,000 to invest and a space to store at most 60 pieces. A table costs him Rs.1500 and a chair Rs.750. Construct the inequations and find the feasible solution.
Question is modified
A furniture dealer deals in tables and chairs. He has ₹ 15,000 to invest and a space to store at most 60 pieces. A table costs him ₹ 150 and a chair ₹ 750. Construct the inequations and find the feasible solution.
Solution:
Let x be the number of tables and y be the number of chairs. Then x ≥ 0, y ≥ 0.
The dealer has a space to store at most 60 pieces.
∴ x + y ≤ 60
Since, the cost of each table is ₹ 150 and that of each chair is ₹ 750, the total cost of x tables and y chairs is 150x + 750y. Since the dealer has ₹ 15,000 to invest, 150x + 750y ≤ 15,000
Hence the system of inequations are
x + y ≤ 60, 150x + 750y ≤ 15000, x ≥ 0, y ≥ 0.
First we draw the lines AB and CD whose equations are x + y = 60 and 150x + 750y = 15,000 respectively.

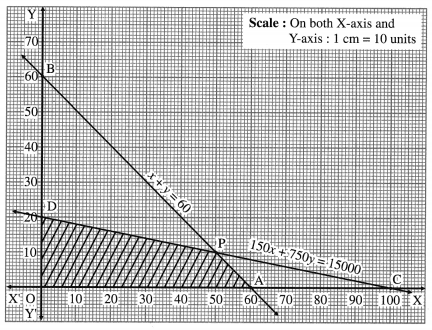
The feasible solution is OAPDO. which is shaded in the graph.

Ex 7.3

Question 1.
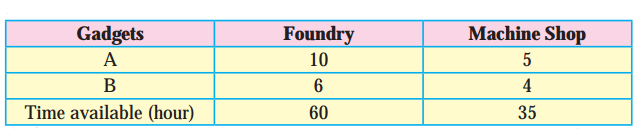
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to machine shop for finishing. The number of man hours of labour required in each shop for production of A and B per unit and the number of man hours available for the firm are as follows :

Profit on the sale of A is ₹ 30 and B is ₹ 20 per units. Formulate the L.P.P. to have maximum profit.
Solution:
Let the number of gadgets A produced by the firm be x and the number of gadgets B produced by the firm be y.
The profit on the sale of A is ₹ 30 per unit and on the sale of B is ₹ 20 per unit.
∴ total profit is z = 30x + 20y.
This is a linear function which is to be maximized. Hence it is the objective function.
The constraints are as per the following table :

From the table total man hours of labour required for x units of gadget A and y units of gadget B in foundry is (10x + 6y) hours and total man hours of labour required in machine shop is (5x + 4y) hours.
Since, maximum time avilable in foundry and machine shops are 60 hours and 35 hours respectively.
Therefore, the constraints are 10x + 6y ≤ 60, 5x + 4y ≤ 35. Since, x and y cannot be negative, we have x ≥ 0, y ≥ 0. Hence, the given LPP can be formulated as :
Maximize z = 30x + 20y, subject to 10x + 6y ≤ 60, 5x + 4y ≤ 35, x ≥ 0, y ≥ 0.

Question 2.
In a cattle breading firm, it is prescribed that the food ration for one animal must contain 14, 22 and 1 units of nutrients A, B and C respectively. Two different kinds of fodder are available. Each unit of these two contains the following amounts of these three nutrients :

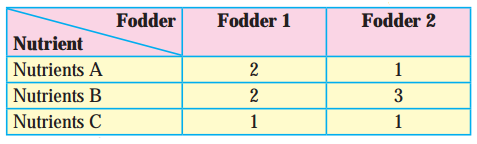
The cost of fodder 1 is ₹3 per unit and that of fodder ₹ 2, Formulate the L.P.P. to minimize the cost.
Solution:
Let x units of fodder 1 and y units of fodder 2 be prescribed.
The cost of fodder 1 is ₹ 3 per unit and cost of fodder 2 is ₹ 2 per unit.
∴ total cost is z = 3x + 2y
This is the linear function which is to be minimized. Hence it is the objective function. The constraints are as per the following table :

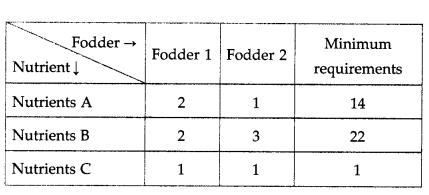
From table fodder contains (2x + y) units of nutrients A, (2x + 3y) units of nutrients B and (x + y) units of nutrients C. The minimum requirements of these nutrients are 14 units, 22 units and 1 unit respectively.
Therefore, the constraints are
2x + y ≥ 14, 2x + 3y ≥ 22, x + y ≥ 1
Since, number of units (i.e. x and y) cannot be negative, we have, x ≥ 0, y ≥ 0.
Hence, the given LPP can be formulated as
Minimize z = 3x + 2y, subject to
2x + y ≥ 14, 2x + 3y ≥ 22, x + y ≥ 1, x ≥ 0, y ≥ 0.

Question 3.
A company manufactures two types of chemicals A and B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B and the total availability of P and Q.

The company gets profits of ₹350 and ₹400 by selling one unit of A and one unit of B respectively. (Assume that the entire production of A and B can be sold). How many units of the chemicals A and B should be manufactured so that the company get maximum profit? Formulate the problem as L.P.P. to maximize the profit.
Solution:
Let the company manufactures x units of chemical A and y units of chemical B. Then the total profit f to the company is p = ₹ (350x + 400y).
This is a linear function which is to be maximized.
Hence, it is the objective function.
The constraints are as per the following table:

The raw material P required for x units of chemical A and y units of chemical B is 3x + 2y. Since, the maximum availability of P is 120, we have the first constraint as 3x + 2y ≤ 120.
Similarly, considering the raw material Q, we have : 2x + 5y ≤ 160.
Since, x and y cannot be negative, we have, x ≥ 0, y ≥ 0.
Hence, the given LPP can be formulated as :
Maximize p = 350x + 400y, subject to
3x + 2y ≤ 120, 2x + 5y ≤ 160, x ≥ 0, y ≥ 0.

Question 4.
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 on magazines A and B per copy. These are processed on three machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II and 2 hours on Machine III. Magazine B requires 3 hours on Machine I, 2 hours on Machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, 60 hours per week respectively. Formulate the L.P.P. to determine weekly production of A and B, so that the total profit is maximum.
Solution:
Let the company prints x magazine of type A and y magazine of type B.
Profit on sale of magazine A is ₹ 10 per copy and magazine B is ₹ 15 per copy.
Therefore, the total earning z of the company is
z = ₹ (10x + 15y).
This is a linear function which is to be maximized.
Hence, it is the objective function.
The constraints are as per the following table:

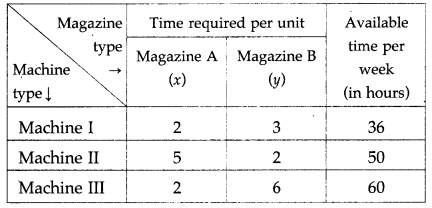
From the table, the total time required for Machine I is (2x + 3y) hours, for Machine II is (5x + 2y) hours and for Machine III is (2x + 6y) hours. The machines I, II, III are available for 36,50 and 60 hours per week. Therefore, the constraints are 2x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60.
Since x and y cannot be negative. We have, x ≥ 0, y ≥ 0. Hence, the given LPP can be formulated as :
Maximize z = 10x + 15y, subject to
2x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60, x ≥ 0, y ≥ 0.

Question 5.
A manufacture produces bulbs and tubes. Each of these must be processed through two machines M₁ and M₂. A package of bulbs require 1 hour of work on Machine M₁ and 3 hours of work on M₂. A package of tubes require 2 hours on Machine M₁ and 4 hours on Machine M₂. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LLP to maximize the profit, if he operates the machine M₁, for atmost 10 hours a day and machine M₂ for atmost 12 hours a day.
Solution:
Let the number of packages of bulbs produced by manufacturer be x and packages of tubes be y. The manufacturer earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes.
Therefore, his total profit is p = ₹ (13.5x + 55y)
This is a linear function which is to be maximized.
Hence, it is the objective function.
The constraints are as per the following table :

From the table, the total time required for Machine M₁ is (x + 2y) hours and for Machine M₂ is (3x + 4y) hours.
Given Machine M₁ and M₂ are available for atmost 10 hours and 12 hours a day respectively.
Therefore, the constraints are x + 2y ≤ 10, 3x + 4y ≤ 12. Since, x and y cannot be negative, we have, x ≥ 0, y ≥ 0. Hence, the given LPP can be formulated as :
Maximize p = 13.5x + 55y, subject to x + 2y ≤ 10, 3x + 4y ≤ 12, x ≥ 0, y ≥ 0.

Question 6.
A company manufactures two types of fertilizers F₁ and F₂. Each type of fertilizer requires
two raw materials A and B. The number of units of A and B required to manufacture one unit of fertilizer F₁ and F₂ and availability of the raw materials A and B per day are given in the
table below :

By selling one unit of F₁ and one unit of F₂, company gets a profit of ₹ 500 and ₹ 750
respectively. Formulate the problem as L.P.P. to maximize the profit.
Solution:
Let the company manufactures x units of fertilizers F₁ and y units of fertilizers F₁. Then the total profit to the company is
z = ₹(500x + 750y).
This is a linear function that is to be maximized. Hence, it is an objective function.

The raw material A required for x units of Fertilizers F₁ and y units of Fertilizers F₂ is 2x + Since the maximum availability of A is 40, we have the first constraint as 2x + 3y ≤ 40.
Similarly, considering the raw material B, we have x + 4y ≤ 70.
Since, x and y cannot be negative, we have, x ≥ 0, y ≥ 0.
Hence, the given LPP can be formulated as:
Maximize z = 500x + 750y, subject to
2x + 3y ≤ 40, x + 4y ≤ 70, x ≥ 0, y ≥ 0.

Question 7.
A doctor has prescribed two different units of foods A and B to form a weekly diet for a sick person. The minimum requirements of fats, carbohydrates and proteins are 18, 28, 14 units respectively. One unit of food A has 4 units of fats. 14 units of carbohydrates and 8 units of protein. One unit of food B has 6 units of fat, 12 units of carbohydrates and 8 units of protein. The price of food A is ₹ 4.5 per unit and that of food B is ₹ 3.5 per unit. Form the L.P.P. so that the sick person’s diet meets the requirements at a minimum cost.
Solution:
Let the diet of sick person include x units of food A and y units of food B.
Then x ≥ 0, y ≥ 0.
The prices of food A and B are ₹ 4.5 and ₹ 3.5 per unit respectively.
Therefore, the total cost is z = ₹ (4.5x + 3.5y)
This is the linear function which is to be minimized.
Hence, it is objective function.
The constraints are as per the following table :

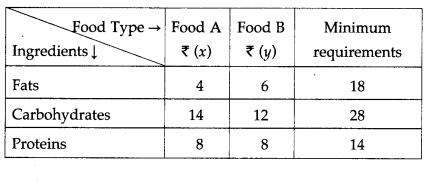
From the table, the sick person’s diet will include (4x + 6y) units of fats, (14x + 12y) units of carbohydrates and (8x + 8y) units of proteins. The minimum requirements of these ingredients are 18 units, 28 units and 14 units respectively.
Therefore, the constraints are
4x + 6y ≥ 18, 14x + 12y ≥ 28, 8x + 8y ≥ 14.
Hence, the given LPP can be formulated as
Minimize z = 4.5x + 3.5y, subject to
4x + 6y ≥ 18, 14x + 12y ≥ 28, 8x + 8y ≥ 14, x ≥ 0, y ≥ 0.

Question 8.
If John drives a car at a speed of 60 kms/hour he has to spend ₹ 5 per km on petrol. If he drives at a faster speed of 90 kms/hour, the cost of petrol increases to ₹ 8 per km. He has ₹ 600 to spend on petrol and wishes to travel the maximum distance within an hour. Formulate the above problem as L.P.P.
Solution:
Let John travel xl km at a speed of 60 km/ hour and x₁ km at a speed of 90 km/hour.
Therefore, time required to travel a distance of x₁ km is x160 hours and the time required to travel a distance of
x₂ km is x290 hours.
∴ total time required to travel is (x160+x290) hours.
Since he wishes to travel the maximum distance within an hour,
x160+x290 ≤ 1
He has to spend ₹ 5 per km on petrol at a speed of 60 km/hour and ₹ 8 per km at a speed of 90 km/hour.
∴ the total cost of travelling is ₹ (5x₁ + 8x₂)
Since he has ₹ 600 to spend on petrol,
5x₁ + 8x₂ ≤ 600
Since distance is never negative, x₁ ≥ 0, x₂ ≥ 0.
Total distance travelled by John is z. = (x₁ + x₂) km.
This is the linear function which is to be maximized.
Hence, it is objective function.
Hence, the given LPP can be formulated as :
Maximize z = x₁ + x₂, subject to
x160+x290 ≤ 1, 5x₁ + 8x₂ ≤ 600, x₁ ≥ 0, x₂ ≥ 0.

Question 9.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be least 5 kg. Cement costs ₹ 20 per kg. and sand costs of ₹ 6 per kg. strength consideration dictate that a concrete brick should contain minimum 4 kg. of cement and not more than 2 kg. of sand. Form the L.P.P. for the cost to be minimum.
Solution:
Let the company use x₁ kg of cement and x₂ kg of sand to make concrete bricks.
Cement costs ₹ 20 per kg and sand costs ₹ 6 per kg.
∴ the total cost c = ₹ (20x₁ + 6x₂)
This is a linear function which is to be minimized.
Hence, it is the objective function.
Total weight of brick = (x₁ + x₂) kg
Since the weight of concrete brick has to be at least 5 kg,
∴ x₁ + x₂ ≥ 5.
Since concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand,
x₁ ≥ 4 and 0 ≤ x₂ ≤ 2
Hence, the given LPP can be formulated as :
Minimize c = 20x₁ + 6x₂, subject to
x₁ + x₂ ≥ 5, x₁ ≥ 4, 0 ≤ x₂ ≤ 2.

Ex 7.4

Question 1.
Maximize : z = 11x + 8y subject to x ≤ 4, y ≤ 6,
x + y ≤ 6, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and ED whose equations are x = 4, y = 6 and x + y = 6 respectively.

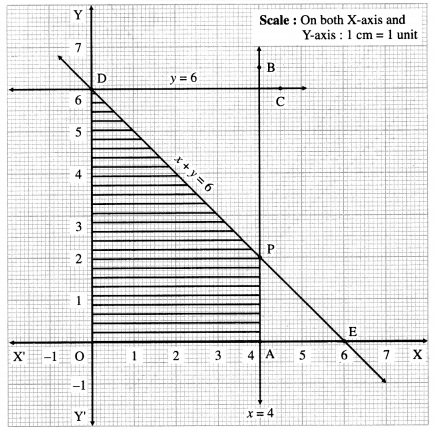
The feasible region is shaded portion OAPDO in the graph.
The vertices of the feasible region are O (0, 0), A (4, 0), P and D (0, 6)
P is point of intersection of lines x + y = 6 and x = 4.
Substituting x = 4 in x + y = 6, we get
4 + y = 6 ∴ y = 2 ∴ P is (4, 2).
∴ the corner points of feasible region are O (0, 0), A (4, 0), P(4, 2) and D(0 ,6).
The values of the objective function z = 11x + 8y at these vertices are
z (O) = 11(0) + 8(0) = 0 + 0 = 0
z(a) = 11(4) + 8(0) = 44 + 0 = 44
z (P) = 11(4) + 8(2) = 44 + 16 = 60
z (D) = 11(0) + 8(2) = 0 + 16 = 16
∴ z has maximum value 60, when x = 4 and y = 2.

Question 2.
Maximize : z = 4x + 6y subject to 3x + 2y ≤ 12,
x + y ≥ 4, x, y ≥ 0.
Solution:
First we draw the lines AB and AC whose equations are 3x + 2y = 12 and x + y = 4 respectively.

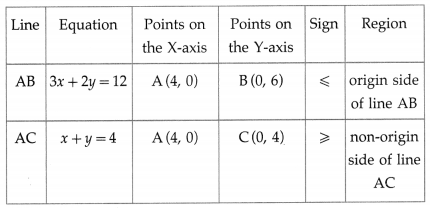
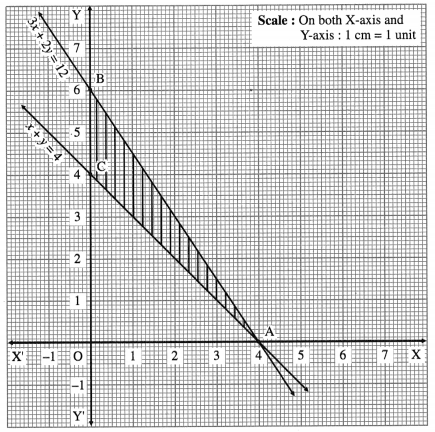
The feasible region is the ∆ABC which is shaded in the graph.
The vertices of the feasible region (i.e. corner points) are A (4, 0), B (0, 6) and C (0, 4).
The values of the objective function z = 4x + 6y at these vertices are
z(a) = 4(4) + 6(0) = 16 + 0 = 16
z(B) = 4(0)+ 6(6) = 0 + 36 = 36
z(C) = 4(0) + 6(4) = 0 + 24 = 24
∴ has maximum value 36, when x = 0, y = 6.

Question 3.
Maximize : z = 7x + 11y subject to 3x + 5y ≤ 26
5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB and CD whose equations are 3x + 5y = 26 and 5x + 3y = 30 respectively.

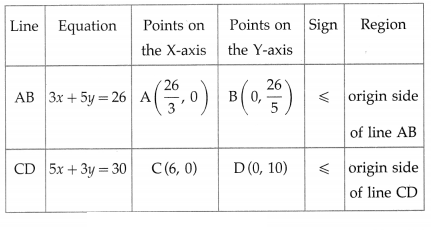
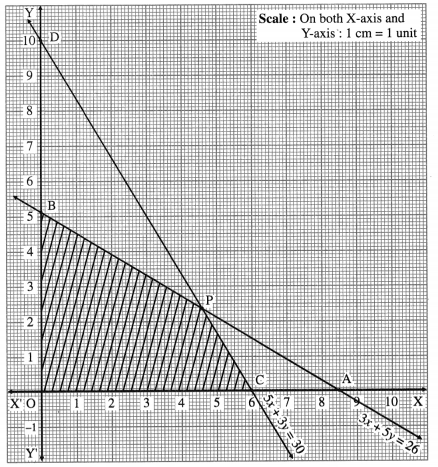
The feasible region is OCPBO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (6, 0), p and B(0, 265)
The vertex P is the point of intersection of the lines
3x + 5y = 26 … (1)
and 5x + 3y = 30 … (2)
Multiplying equation (1) by 3 and equation (2) by 5, we get
9x + 15y = 78
and 25x + 15y = 150
On subtracting, we get
16x = 72 ∴ x = 7216=92 = 4.5
Substituting x = 4.5 in equation (2), we get
5(4.5) + 3y = 30
22.5 + 3y = 30
∴ 3y = 7.5 ∴ y = 2.5
∴ P is (4.5, 2.5)
The values of the objective function z = 7x + 11y at these corner points are
z (O) = 7(0) + 11(0) = 0 + 0 = 0
z (C) = 7(6) + 11(0) = 42 + 0 = 42
z (P) = 7(4.5) + 11 (2.5) = 31.5 + 27.5 = 59.0 = 59
z(B) = 7(0) + 11(265)=2865 = 57.2
∴ z has maximum value 59, when x = 4.5 and y = 2.5.

Question 4.
Maximize : z = 10x + 25y subject to 0 ≤ x ≤ 3,
0 ≤ y ≤ 3, x + y ≤ 5 also find maximum value of z.
Solution:
First we draw the lines AB, CD and EF whose equations are x = 3, y = 3 and x + y = 5 respectively.

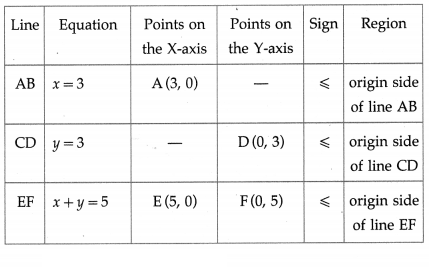
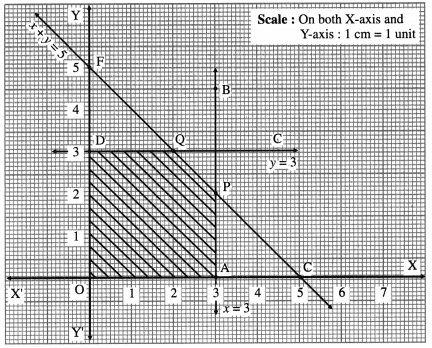
The feasible region is OAPQDO which is shaded in the i graph.
The vertices of the feasible region are O (0, 0), A (3, 0), P, Q and D(0, 3).
t P is the point of intersection of the lines x + y = 5 and x = 3.
Substituting x = 3 in x + y = 5, we get
3 + y = 5 ∴ y = 2
∴ P is (3, 2)
Q is the point of intersection of the lines x + y = 5 and y = 3
Substituting y = 3 in x + y = 5, we get
x + 3 = 5 ∴ x = 2
∴ Q is (2, 3)
The values of the objective function z = 10x + 25y at these vertices are
z(O) = 10(0) + 25(0) = 0 + 0 = 0
z(a) = 10(3) + 25(0) = 30 + 0 = 30
z(P) = 10(3) + 25(2) = 30 + 50 = 80
z(Q) = 10(2) + 25(3) = 20 + 75 = 95
z(D) = 10(0)+ 25(3) = 0 + 75 = 75
∴ z has maximum value 95, when x = 2 and y = 3.

Question 5.
Maximize : z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21,
x + y ≤ 9, x ≥ 0, y ≥ 0 also find maximum value of z.
Solution:
First we draw the lines AB, CD and EF whose equations are x + 4y = 24, 3x + y = 21 and x + y = 9 respectively.

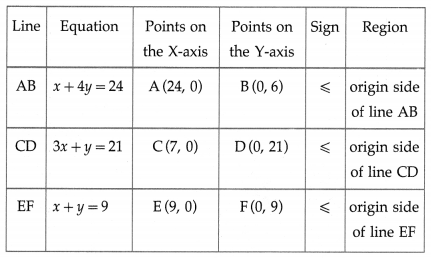
The feasible region is OCPQBO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (7, 0), P, Q and B (0, 6).
P is the point of intersection of the lines
3x + y = 21 … (1)
and x + y = 9 … (2)
On subtracting, we get 2x = 12 ∴ x = 6
Substituting x = 6 in equation (2), we get
6 + y = 9 ∴ y = 3
∴ P = (6, 3)
Q is the point of intersection of the lines
x + 4y = 24 … (3)
and x + y = 9 … (2)
On subtracting, we get
3y = 15 ∴ y = 5
Substituting y = 5 in equation (2), we get
x + 5= 9 ∴ x = 4
∴ Q = (4, 5)
∴ the corner points of the feasible region are 0(0,0), C(7, 0), P (6, 3), Q (4, 5) and B (0, 6).
The values of the objective function 2 = 3x + 5y at these corner points are
z(O) = 3(0)+ 5(0) = 0 + 0 = 0
z(C) = 3(7) + 5(0) = 21 + 0 = 21
z(P) = 3(6) + 5(3) = 18 + 15 = 33
z(Q) = 3(4) + 5(5) = 12 + 25 = 37
z(B) = 3(0)+ 5(6) = 0 + 30 = 30
∴ z has maximum value 37, when x = 4 and y = 5.

Question 6.
Minimize : z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3,
x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB and CD whose equations are 5x + y = 5 and x + y = 3 respectively.

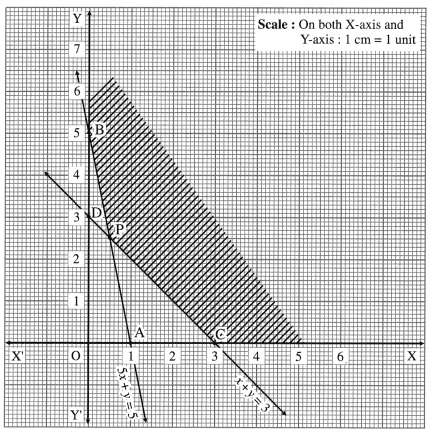
The feasible region is XCPBY which is shaded in the graph.
The vertices of the feasible region are C (3, 0), P and B (0, 5).
P is the point of the intersection of the lines
5x + y = 5
and x + y = 3
On subtracting, we get
4x = 2 ∴ x = 12
Substituting x = 12 in x + y = 3, we get
12 + y = 3
∴ y = 52 ∴ P = (12,52)
The values of the objective function z = 7x + y at these vertices are
z(C) = 7(3) + 0 = 21
z(B) = 7(0) + 5 = 5
∴ z has minimum value 5, when x = 0 and y = 5.

Question 7.
Minimize : z = 8x + 10y subject to 2x + y ≥ 7, 2x + 3y ≥ 15,
y ≥ 2, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and EF whose equations are 2x + y = 7, 2x + 3y = 15 and y = 2 respectively.

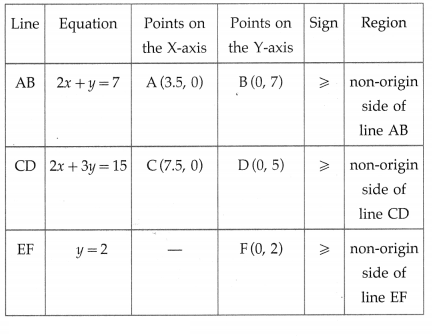
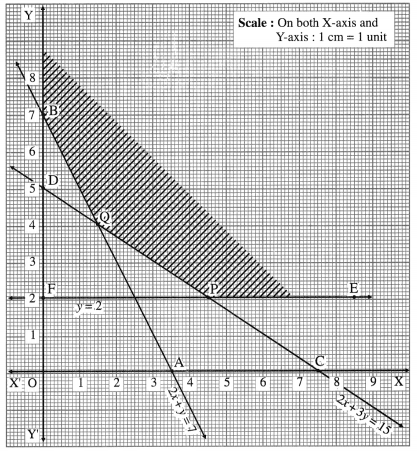
The feasible region is EPQBY which is shaded in the graph. The vertices of the feasible region are P, Q and B(0,7). P is the point of intersection of the lines 2x + 3y = 15 and y = 2.
Substituting y – 2 in 2x + 3y = 15, we get 2x + 3(2) = 15
∴ 2x = 9 ∴ x = 4.5 ∴ P = (4.5, 2)
Q is the point of intersection of the lines
2x + 3y = 15 … (1)
and 2x + y = 7 … (2)
On subtracting, we get
2y = 8 ∴ y = 4
∴ from (2), 2x + 4 = 7
∴ 2x = 3 ∴ x = 1.5
∴ Q = (1.5, 4)
The values of the objective function z = 8x + 10y at these vertices are
z(P) = 8(4.5) + 10(2) = 36 + 20 = 56
z(Q) = 8(1.5) + 10(4) = 12 + 40 = 52
z(B) = 8(0) +10(7) = 70
∴ z has minimum value 52, when x = 1.5 and y = 4

Question 8.
Minimize : z = 6x + 21y subject to x + 2y ≥ 3, x + 4y ≥ 4,
3x + y ≥ 3, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and EF whose equations are x + 2y = 3, x + 4y = 4 and 3x + y = 3 respectively.

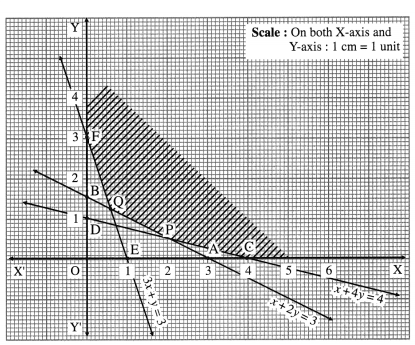
The feasible region is XCPQFY which is shaded in the graph.
The vertices of the feasible region are C (4, 0), P, Q and F(0, 3).
P is the point of intersection of the lines x + 4y = 4 and x + 2y = 3
On subtracting, we get

Download PDF

Maharashtra Board Solutions Class 12-Arts & Science Maths (Part 1): Chapter 7- Linear Programming

Download PDF: Maharashtra Board Solutions Class 12-Arts & Science Maths (Part 1): Chapter 7- Linear Programming PDF

Chapterwise Maharashtra Board Solutions Class 12 Arts & Science Maths (Part 1) :

• Chapter 1- Mathematical Logic
• Chapter 2- Matrices
• Chapter 3- Trigonometric Functions
• Chapter 4- Pair of Straight Lines
• Chapter 5- Vectors
• Chapter 6- Line and Plane
• Chapter 7- Linear Programming

FAQs

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC. 

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.

Read More

• NCERT Solutions for 12th Class Maths: Chapter 12-Linear Programming
• RD Sharma Solutions for Class 11 Maths Chapter 15–Linear Inequations
• RD Sharma Solutions for Class 6 Maths Chapter 6–Fractions
• RD Sharma Solutions for Class 10 Maths Chapter 8–Quadratic Equations
• RD Sharma Solutions for Class 11 Maths Chapter 3–Functions

IndCareer Board Book Solutions App

IndCareer Board Book App provides complete study materials for students from classes 1 to 12 of Board. The App contains complete solutions of NCERT books, notes, and other important materials for students. Download the IndCareer Board Book Solutions now.