Maharashtra Board Solutions Class 12-Arts & Science Maths (Part 1): Chapter 1- Mathematical Logic

Class 12: Maths Chapter 1 solutions. Complete Class 12 Maths Chapter 1 Notes.

Maharashtra Board Solutions Class 12-Arts & Science Maths (Part 1): Chapter 1- Mathematical Logic

Maharashtra Board 12th Maths Chapter 1, Class 12 Maths Chapter 1 solutions

Ex 1.1

Question 1.
State which of the following sentences are statements. Justify your answer. In case of statement, write down the truth value :
(i) 5 + 4 = 13.
Solution:
It is a statement which is false, hence its truth value is ‘F’.

(ii) x – 3 = 14.
Solution:
It is an open sentence, hence it is not a statement.

(iii) Close the door.
Solution:
It is an imperative sentence, hence it is not a statement.

(iv) Zero is a complex number.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(v) Please get me breakfast.
Solution:
It is an imperative sentence, hence it is not a statement.

(vi) Congruent triangles are also similar.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(vii) x² = x.
Solution:
It is an open sentence, hence it is not a statement,

(viii) A quadratic equation cannot have more than two roots.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(ix) Do you like Mathematics ?
Solution:
It is an interrogative sentence, hence it is not a statement.

(x) The sun sets in the west.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(xi) All real numbers are whole numbers.
Solution:
It is a statement which is false, hence its truth value is ‘F’.

(xii) Can you speak in Marathi ?
Solution:
It is an interrogative sentence, hence it is not a statement.

(xiii) x² – 6x – 7 = 0, when x = 7.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(xiv) The sum of cuberoots of unity is zero.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(xv) It rains heavily.
Solution :
It is an open sentence, hence it is not a statement.

Question 2.
Write the following compound statements symbolically:
(i) Nagpur is in Maharashtra and Chennai is in Tamil Nadu.
Solution:
Let p : Nagpur is in Maharashtra.
q : Chennai is in Tamil Nadu.
Then the symbolic form of the given statement is P∧q.

(ii) Triangle is equilateral or isosceles,
Solution:
Let p : Triangle is equilateral.
q : Triangle is isosceles.
Then the symbolic form of the given statement is P∨q.

(iii) The angle is right angle if and only if it is of measure 90°.
Solution:
Let p : The angle is right angle.
q : It is of measure 90°.
Then the symbolic form of the given statement is p↔q

(iv) Angle is neither acute nor obtuse.
Solution:
Let p : Angle is acute.
q : Angle is obtuse.
Then the symbolic form of the given statement is
~p ∧ ~q.

(v) If ∆ ABC is right angled at B, then m∠A + m∠C = 90°.
Solution:
Let p : ∆ ABC is right angled at B.
q : m∠A + m∠C = 90°.
Then the symbolic form of the given statement is p → q

(vi) Hima Das wins gold medal if and only if she runs fast.
Solution:
Let p : Hima Das wins gold medal
q : She runs fast.
Then the symbolic form of the given statement is p ↔ q.

(vii) x is not irrational number but it is a square of an integer.
Solution:
Let p : x is not irrational number
q : It is a square of an integer
Then the symbolic form of the given statement is p ∧ q
Note : If p : x is irrational number, then the symbolic form of the given statement is ~p ∧ q.

Question 3.
Write the truth values of the following :
(i) 4 is odd or 1 is prime.
Solution:
Let p : 4 is odd.
q : 1 is prime.
Then the symbolic form of the given statement is p∨q.
The truth values of both p and q are F.
∴ the truth value of p v q is F. … [F ∨ F = F]

(ii) 64 is a perfect square and 46 is a prime number.
Solution:
Let p : 64 is a perfect square.
q : 46 is a prime number.
Then the symbolic form of the given statement is p∧q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F]

(iii) 5 is a prime number and 7 divides 94.
Solution:
Let p : 5 is a prime number.
q : 7 divides 94.
Then the symbolic form of the given statement is p∧q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F]

(iv) It is not true that 5 – 3i is a real number.
Solution:
Let p : 5 – 3i is a real number.
Then the symbolic form of the given statement is ~ p.
The truth values of p is F.
∴ the truth values of ~ p is T. … [~ F ≡ T]

(v) If 3 × 5 = 8, then 3 + 5 = 15.
Solution:
Let p : 3 × 5 = 8.
q : 3 + 5 = 15.
Then the symbolic form of the given statement is p → q.
The truth values of both p and q are F.
∴ the truth value of p → q is T. … [F → F ≡ T]

(vi) Milk is white if and only if sky is blue.
Solution:
Let p : Milk is white.
q : Sky is blue
Then the symbolic form of the given statement is p ↔ q.
The truth values of both p and q are T.
∴ the truth value of p ↔ q is T. … [T ↔ T ≡ T]

(vii) 24 is a composite number or 17 is a prime number.
Solution :
Let p : 24 is a composite number.
q : 17 is a prime number.
Then the symbolic form of the given statement is p ∨ q.
The truth values of both p and q are T.
∴ the truth value of p ∨ q is T. … [T ∨ T ≡ T]

Question 4.
If the statements p, q are true statements and r, s are false statements, then determine the truth values of the following:
(i) p ∨ (q ∧ r)
Solution:
Truth values of p and q are T and truth values of r and s are F.
p ∨ (q ∧ r) ≡ T ∨ (T ∧ F)
≡ T ∧ F ≡ T
Hence the truth value of the given statement is true.

(ii) (p → q) ∨ (r → s)
Solution:
(p → q) ∨ (r → s) ≡ (T → T) ∨ (F → F)
≡ T ∨ T ≡ T
Hence the truth value of the given statement is true.

(iii) (q ∧ r) ∨ (~p ∧ s)
Solution:
(q ∧ r) ∨ (~p ∧ s) ≡ (T ∧ F) ∨ (~T ∧ F)
≡ F ∨ (F ∧ F)
≡ F ∨ F ≡ F
Hence the truth value of the given statement is false.

(iv) (p → q) ∧ (~ r)
Solution:
(p → q) ∧ (~ r) ≡ (T → T) ∧ (~ F)
≡ T ∧ T ≡ T
Hence the truth value of the given statement is true.

(v) (~r ↔ p) → (~q)
Solution:
(~r ↔ p) → (~q) ≡ (~F ↔ T) → (~T)
≡ (T ↔ T) → F
≡ T → F ≡ F
Hence the truth value of the given statement is false.

(vi) [~p ∧ (~q ∧ r) ∨ (q ∧ r) ∨ (p ∧ r)]
Solution:
[~p ∧ (~q ∧ r)∨(q ∧ r)∨(p ∧ r)]
≡ [~T ∧ (~T ∧ F)] ∨ [(T ∧ F) V (T ∧ F)]
≡ [F ∧ (F ∧ F)] ∨ [F V F]
≡ (F ∧ F) ∨ F
≡ F ∨ F ≡ F
Hence the truth value of the given statement is false.

(vii) [(~ p ∧ q) ∧ (~ r)] ∨ [(q → p) → (~ s ∨ r)]
Solution:
[(~ p ∧ q) ∧ (~ r)] ∨ [(q → p) → (~ s ∨ r)]
≡ [(~T ∧ T) ∧ (~F)] ∨ [(T → T) → (~F ∨ F)]
≡ [(F ∧ T) ∧ T] ∨ [T → (T ∨ F)]
≡ (F ∧ T) ∨ (T → T)
≡ F ∨ T ≡ T
Hence the truth value of the given statement is true.

(viii) ~ [(~p ∧ r) ∨ (s → ~q)] ↔ (p ∧ r)
Solution :
~ [(~p ∧ r) ∨ (s → ~q)] ↔ (p ∧ r)
≡ ~ [(~T ∧ F) ∨ (F → ~T)] ↔ (T ∧ F)
≡ ~ [(F ∧ F) ∨ (F → F)] ↔ F
≡ ~ (F ∨ T) ↔ F
≡ ~T ↔ F
≡ F ↔ F ≡ T
Hence the truth value of the given statement is true.

Question 5.
Write the negations of the following :
(i) Tirupati is in Andhra Pradesh.
Solution:
The negations of the given statements are :
Tirupati is not in Andhra Pradesh.

(ii) 3 is not a root of the equation x² + 3x – 18 = 0.
Solution:
3 is a root of the equation x² + 3x – 18 = 0.

(iii) 2–√ is a rational number.
Solution:
2–√ is not a rational number.

(iv) Polygon ABCDE is a pentagon.
Solution:
Polygon ABCDE is not a pentagon.

(v) 7 + 3 > 5.
Solution :
7 + 3 > 5.

Ex 1.2

Question 1.
Construct the truth table for each of the following statement patterns:
(i) [(p → q) ∧ q] → p
Solution :
Here are two statements and three connectives.
∴ there are 2 × 2 = 4 rows and 2 + 3 = 5 columns in the truth table.

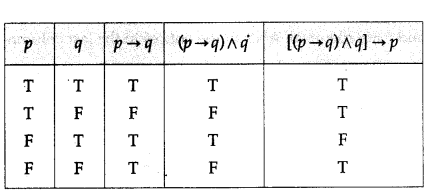
(ii) (p ∧ ~q) ↔ (p → q)
Solution:

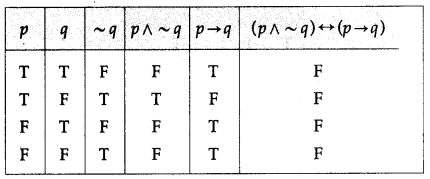
(iii) (p ∧ q) ↔ (q ∨ r)
Solution:

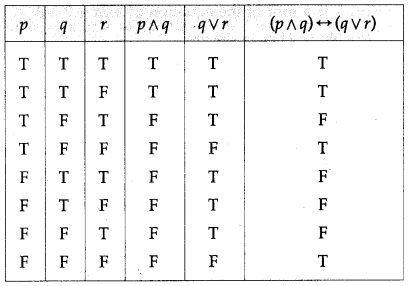
(iv) p → [~(q ∧ r)]
Solution:

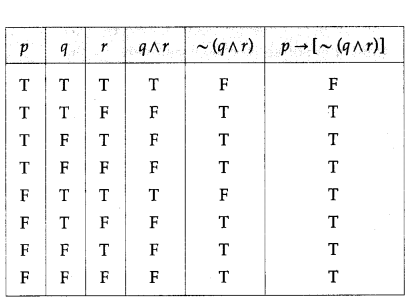
(v) ~p ∧ [(p ∨ ~q ) ∧ q]
Solution:

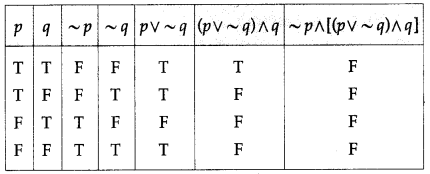
(vi) (~p → ~q) ∧ (~q → ~p)
Solution:

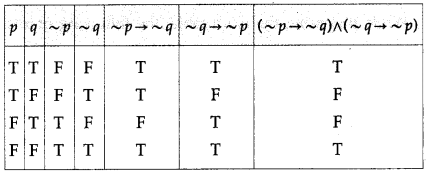
(vii) (q → p) ∨ (~p ↔ q)
Solution:

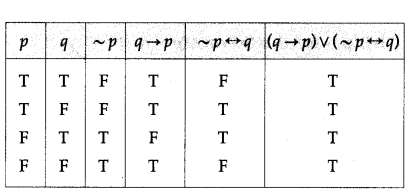
(viii) [p → (q → r)] ↔ [(p ∧ q) → r]
Solution:

(ix) p → [~(q ∧ r)]
Solution:

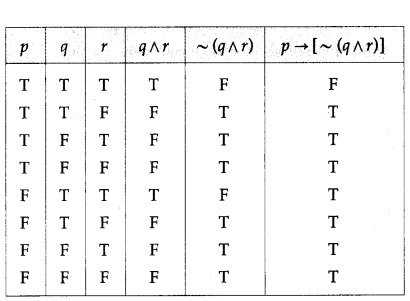
(x) (p ∨ ~q) → (r ∧ p)
Solution:

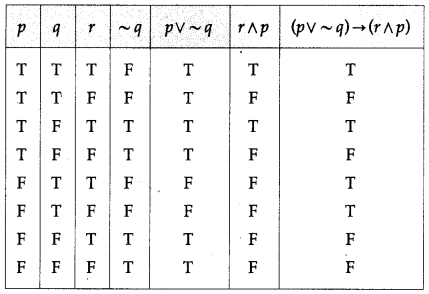
Question 2.
Using truth tables prove the following logical equivalences.
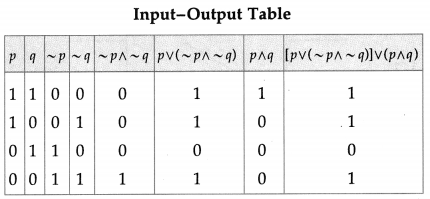
(i) ~p ∧ q ≡ (p ∨ q) ∧ ~p
Solution:

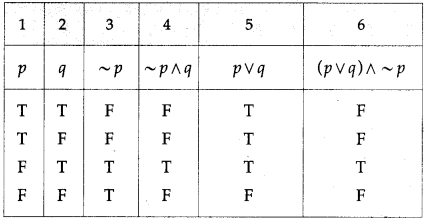
The entries in the columns 4 and 6 are identical.
∴ ~p ∧ q ≡ (p ∨ q) ∧ ~p.

(ii) ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p
Solution:

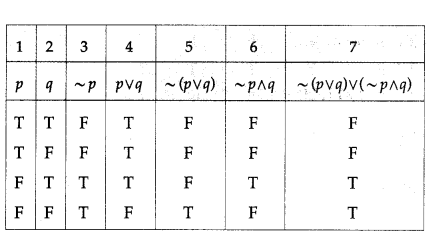
The entries in the columns 3 and 7 are identical.
∴ ~(p ∨ q) ∧ (~p ∧ q) = ~p.

(iii) p ↔ q ≡ ~[(p ∨ q) ∧ ~(p ∧ q)]
Solution:

The entries in the columns 3 and 8 are identical.
∴ p ↔ q ≡ ~[(p ∨ q) ∧ ~(p ∧ q)].

(iv) p → (q → p) ≡ ~p → (p → q)
Solution:

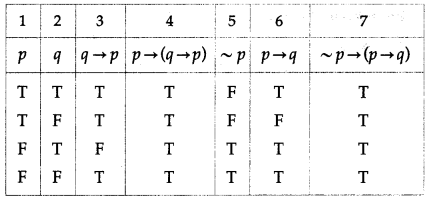
The entries in the columns 4 and 7 are identical.
∴ p → (q → p) ≡ ~p → (p → q).

(v) (p ∨ q ) → r ≡ (p → r) ∧ (q → r)
Solution:

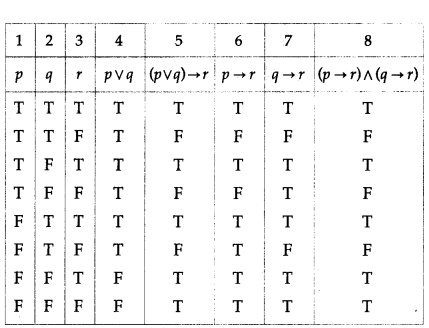
The entries in the columns 5 and 8 are identical.
∴ (p ∨ q ) → r ≡ (p → r) ∧ (q → r).

(vi) p → (q ∧ r) ≡ (p → q) ∧ (p → r)
Solution:

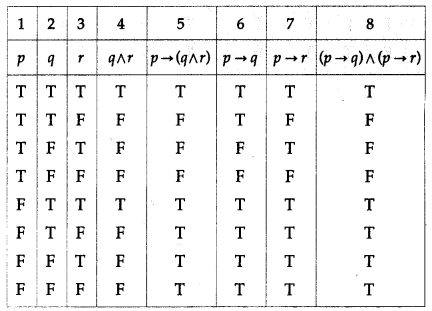
The entries in the columns 5 and 8 are identical.
∴ p → (q ∧ r) ≡ (p → q) ∧ (p → r).

(vii) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
Solution:

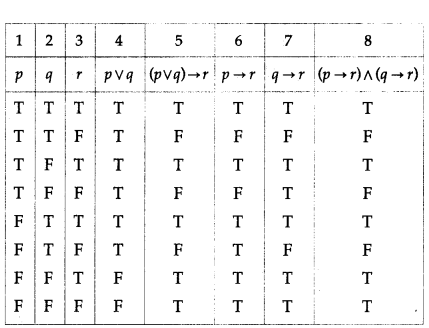
The entries in the columns 5 and 8 are identical.
∴ p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r).

(viii) [~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r
Solution:

The entries in the columns 3 and 7 are identical.
∴ [~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r.

(ix) ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p)
Solution:

The entries in the columns 6 and 9 are identical.
∴ ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p).

Question 3.
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
(i) (p ∧ q) → (q ∨ p)
Solution:

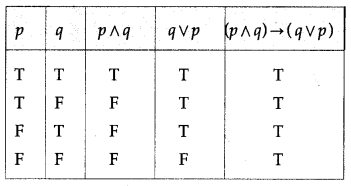
All the entries in the last column of the above truth table are T.
∴ (p ∧ q) → (q ∨ p) is a tautology.

(ii) (p → q) ↔ (~p ∨ q)
Solution:

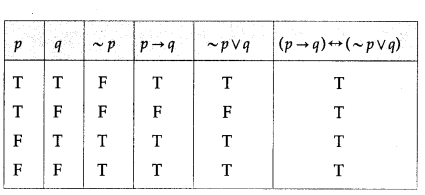
All the entries in the last column of the above truth table are T.
∴ (p → q) ↔ (~p ∨ q) p is a tautology.

(iii) [~(~p ∧ ~q)] ∨ q
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ [~(~p ∧ ~q)] ∨ q is a contingency.

(iv) [(p → q) ∧ q)] → p
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ [(p → q) ∧ q)] → p is a contingency

(v) [(p → q) ∧ ~q] → ~p
Solution:

All the entries in the last column of the above truth table are T.
∴ [(p → q) ∧ ~q] → ~p is a tautology.

(vi) (p ↔ q) ∧ (p → ~q)
Solution:

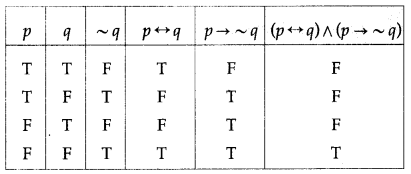
The entries in the last column of the above truth table are neither all T nor all F.
∴ (p ↔ q) ∧ (p → ~q) is a contingency.

(vii) ~(~q ∧ p) ∧ q
Solution:

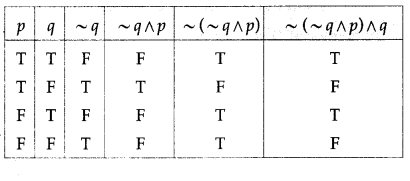
The entries in the last column of the above truth table are neither all T nor all F.
∴ ~(~q ∧ p) ∧ q is a contingency.

(viii) (p ∧ ~q) ↔ (p → q)
Solution:

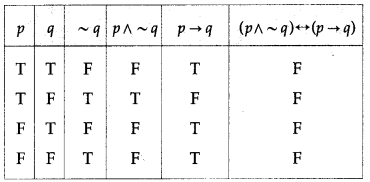
All the entries in the last column of the above truth table are F.
∴ (p ∧ ~q) ↔ (p → q) is a contradiction.

(ix) (~p → q) ∧ (p ∧ r)
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ (~p → q) ∧ (p ∧ r) is a contingency.

(x) [p → (~q ∨ r)] ↔ ~[p → (q → r)]
Solution:

All the entries in the last column of the above truth table are F.
∴ [p → (~q ∨ r)] ↔ ~[p → (q → r)] is a contradiction

Ex 1.3

Question 1.
If A = {3, 5, 7, 9, 11, 12}, determine the truth value of each of the following.
(i) Ǝ x ∈ A such that x – 8 = 1
Solution:
Clearly x = 9 ∈ A satisfies x – 8 = 1. So the given statement is true, hence its truth value is T.

(ii) Ɐ x ∈ A, x² + x is an even number
Solution:
For each x ∈ A, x² + x is an even number. So the given statement is true, hence its truth value is T.

(iii) Ǝ x ∈ A such that x² < 0
Solution:
There is no x ∈ A which satisfies x² < 0. So the given statement is false, hence its truth value is F.

(iv) Ɐ x ∈ A, x is an even number
Solution:
x = 3 ∈ A, x = 5 ∈ A, x = 7 ∈ A, x = 9 ∈ A, x = 11 ∈ A do not satisfy x is an even number. So the given statement is false, hence its truth value is F.

(v) Ǝ x ∈ A such that 3x + 8 > 40
Solution:
Clearly x = 11 ∈ A and x = 12 ∈ A satisfies 3x + 8 > 40. So the given statement is true, hence its truth value is T.

(vi) Ɐ x ∈ A, 2x + 9 > 14
Solution:
For each x ∈ A, 2x + 9 > 14. So the given statement is true, hence its truth value is T.

Question 2.
Write the duals of each of the following.
(i) p ∨ (q ∧ r)
Solution:
The duals of the given statement patterns are :
p ∧ (q ∨ r)

(ii) p ∧ (q ∧ r)
Solution:
p ∨ (q ∨ r)

(iii) (p ∨ q) ∧ (r ∨ s)
Solution:
(p ∧ q) ∨ (r ∧ s)

(iv) p ∧ ~q
Solution:
p ∨ ~q

(v) (~p ∨ q) ∧ (~r ∧ s)
Solution:
(~p ∧ q) ∨ (~r ∨ s)

(vi) ~p ∧ (~q ∧ (p ∨ q) ∧ ~r)
Solution:
~p ∨ (~q ∨ (p ∧ q) ∨ ~r)

(vii) [~(p ∨ q)] ∧ [p ∨ ~(q ∧ ~s)]
Solution:
[ ~(p ∧ q)] ∨ [p ∧ ~(q ∨ ~s)]

(viii) c ∨ {p ∧ (q ∨ r)}
Solution:
t ∧ {p ∧ (q Ar)}

(ix) ~p ∨ (q ∧ r) ∧ t
Solution:
~p ∧ (q ∨ r) ∨ c

(x) (p ∨ q) ∨ c
Solution:
(p ∧ q) ∧ t

Question 3.
Write the negations of the following.
(i) x + 8 > 11 or y – 3 = 6
Solution:
Let p : x + 8 > 11, q : y — 3 = 6.
Then the symbolic form of the given statement is p ∨ q.
Since ~(p ∨ q) ≡ ~p ∧ ~q, the negation of given statement is :
‘x + 8 > 11 and y – 3 ≠ 6’ OR
‘x + 8 ≮ 11 and y – 3 ≠ 6’

(ii) 11 < 15 and 25 > 20
Solution:
Let p: 11 < 15, q : 25 > 20.
Then the symbolic form of the given statement is p ∧ q.
Since ~(p ∧ q) ≡ ~p ∨ ~q, the negation of given statement is :
’11 ≮ 15 or 25 > 20.’ OR
’11 ≯ 15 or 25 ≮ 20.’

(iii) Qudrilateral is a square if and only if it is a rhombus.
Solution:
Let p : Quadrilateral is a square.
q : It is a rhombus.
Then the symbolic form of the given statement is p ↔ q.
Since ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p), the negation of given statement is :
‘ Quadrilateral is a square but it is not a rhombus or quadrilateral is a rhombus but it is not a square.’

(iv) It is cold and raining.
Solution:
Let p : It is cold.
q : It is raining.
Then the symbolic form of the given statement is p ∧ q.
Since ~(p ∧ q) ≡ ~p ∨ ~q, the negation of the given statement is :
‘It is not cold or not raining.’

(v) If it is raining then we will go and play football.
Solution:
Let p : It is raining.
q : We will go.
r : We play football.
Then the symbolic form of the given statement is p → (q ∧ r).
Since ~[p → (q ∧ r)] ≡ p ∧ ~(q ∧ r) ≡ p ∧ (q ∨ ~r), the negation of the given statement is :
‘It is raining and we will not go or not play football.’

(vi) 2–√ is a rational number.
Solution:
Let p : 2–√ is a rational number.
The negation of the given statement is
‘ ~p : 2–√ is not a rational number.’

(vii) All natural numbers are whole numers.
Solution:
The negation of the given statement is :
‘Some natural numbers are not whole numbers.’

(viii) Ɐ n ∈ N, n² + n + 2 is divisible by 4.
Solution:
The negation of the given statement is :
‘Ǝ n ∈ N, such that n² + n + 2 is not divisible by 4.’

(ix) Ǝ x ∈ N such that x – 17 < 20
Solution:
The negation of the given statement is :
‘Ɐ x ∈ N, x – 17 ≯ 20.’

Question 4.
Write converse, inverse and contrapositive of the following statements.
(i) If x < y then x² < y² (x, y ∈ R)
Solution:
Let p : x < y, q : x² < y².
Then the symbolic form of the given statement is p → q.
Converse : q → p is the converse of p → q.
i.e. If x² < y², then x < y.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If x ≯ y, then x² ≯ y². OR
If x ≮ y, then x² ≮ y².
Contrapositive : ~q → p is the contrapositive of
p → q i.e. If x² ≯ y², then x ≯ y. OR
If x² ≮ y², then x ≮ y.

(ii) A family becomes literate if the woman in it is literate.
Solution:
Let p : The woman in the family is literate.
q : A family become literate.
Then the symbolic form of the given statement is p → q
Converse : q → p is the converse of p → q.
i.e. If a family become literate, then the woman in it is literate.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If the woman in the family is not literate, then the family does not become literate.
Contrapositive : ~q → ~p is the contrapositive of p → q. i e. If a family does not become literate, then the woman in it is not literate.

(iii) If surface area decreases then pressure increases.
Solution:
Let p : The surface area decreases.
q : The pressure increases.
Then the symbolic form of the given statement is p → q.
Converse : q → p is the converse of p→ q.
i.e. If the pressure increases, then the surface area decreases.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If the surface area does not decrease, then the pressure does not increase.
Contrapositive : ~q → ~p is the contrapositive of p → q.
i.e. If the pressure does not increase, then the surface area does not decrease.

(iv) If voltage increases then current decreases.
Solution:
Let p : Voltage increases.
q : Current decreases.
Then the symbolic form of the given statement is p → q.
Converse : q →p is the converse of p → q.
i.e. If current decreases, then voltage increases.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If voltage does not increase, then current does not decrease.
Contrapositive : ~q → ~p, is the contrapositive of p → q.
i.e. If current does not decrease, then voltage doesnot increase.

Ex 1.4

Question 1.
Using rules of negation write the negations of the following with justification.
(i) ~q → p
Solution:
The negation of ~q → p is
~(~q → p) ≡ ~ q ∧ ~p…. (Negation of implication)

(ii) p ∧ ~q
Solution:
The negation of p ∧ ~q is
~(p ∧ ~q) ≡ ~p ∨ ~(~q) … (Negation of conjunction)
≡ ~ p ∨ q … (Negation of negation)

(iii) p ∨ ~q
Solution:
The negation of p ∨ ~ p is
~ (p ∨ ~(q) ≡ ~p ∧ ~(~(q) … (Negation of disjunction)
≡ ~ p ∧ q … (Negation of negation)

(iv) (p ∨ ~q) ∧ r
Solution:
The negation of (p ∨ ~ q) ∧ r is
~[(p ∨ ~q) ∧ r] ≡ ~(p ∨ ~q) ∨ ~r … (Negation of conjunction)
≡ [ ~p ∧ ~(~q)] ∨ ~ r… (Negation of disjunction)
≡ (~ p ∧ q) ∧ ~ r … (Negation of negation)

(v) p → (p ∨ ~q)
Solution:
The negation of p → (p ∨ ~q) is
~ [p → (p ∨ ~q)] ≡ p ∧ ~ (p ∧ ~p) … (Negation of implication)
≡ p ∧ [ ~ p ∧ ~ (~(q)] … (Negation of disjunction)
≡ p ∧ (~ p ∧ q) (Negation of negation)

(vi) ~(p ∧ q) ∨ (p ∨ ~q)
Solution:
The negation of ~(p ∧ q) ∨ (p ∨ ~q) is
~[~(p ∧ q) ∨ (p ∨ ~q)] ≡ ~[~(p ∧ q)] ∧ ~(p ∨ ~q) … (Negation of disjunction)
≡ ~[~(p ∧ q)] ∧ [ p ∧ ~(~q)] … (Negation of disjunction)
≡ (p ∧ q) ∧ (~ p ∧ q) … (Negation of negation)

(vii) (p ∨ ~q) → (p ∧ ~q)
Solution:
The negation of (p ∨ ~q) → (p ∧ ~q) is
~[(p ∨ ~q) → (p ∧ ~q)]
≡ (p ∨ ~q) ∧ ~(p ∧ ~q) … (Negation of implication)
≡ (p ∨ ~q) ∧ [ ~p ∨ ~(~q)] … (Negation of conjunction)
≡ (p ∨ ~q) ∧ (~p ∨ q) … (Negation of negation)

(viii) (~ p ∨ ~q) ∨ (p ∧ ~q)
Solution:
The negation of (~ p ∨ ~q) ∨ (p ∧ ~ q) is
~ [(~p ∨ ~q) ∨ (p ∧ ~ q)]
≡ ~(~p ∨ ~q) ∧ ~(p ∧ ~q) … (Negation of disjunction)
≡ [~(~p) ∧ ~(~q)] ∧ [~p ∨ ~(~q)] … (Negation of disjunction and conjunction)
≡ (p ∧ q) ∧ (~p ∨ q) … (Negation of negation)

Question 2.
Rewrite the following statements without using if .. then.
(i) If a man is a judge then he is honest.
Solution:
Since p → ≡ ~p ∨ q, the given statements can be written as :
A man is not a judge or he is honest.

(ii) It 2 is a rational number then 2–√ is irrational number.
Solution:
2 is not a rational number or 2–√ is irrational number.

(iii) It f(2) = 0 then f(x) is divisible by (x – 2).
Solution:
f(2) ≠ 0 or f(x) is divisible by (x – 2).

Question 3.
Without using truth table prove that :
(i) p ↔ q ≡ (p∧ q) ∨ (~ p ∧ ~q)
Solution:
LHS = p ↔ q
≡ (p ↔ q) ∧ (q ↔ p) … (Biconditional Law)
≡ (~p ∨ q) ∧ (~q ∨ p) … (Conditional Law)
≡ [~p ∧ (~q ∨ p)] ∨ [q ∧ (~q ∨ p)] … (Distributive Law)
≡ [(~p ∧ ~q) ∨ (~p ∧ p)] ∨ [(q ∧ ~q) ∨ (q ∧ p)] … (Distributive Law)
≡ [(~p ∧ ~q) ∨ F] ∨ [F ∨ (q ∧ p)] … (ComplementLaw)
≡ (~ p ∧ ~ q) ∨ (q ∧ p) … (Identity Law)
≡ (~ p ∧ ~ q) ∨ (p ∧ q) … (Commutative Law)
≡ (p ∧ q) ∨ (~p ∧ ~q) … (Commutative Law)
≡ RHS.

(ii) (p ∨ q) ∧ (p ∨ ~q) ≡ p
Solution:
LHS = (p ∨ q) ∧ (p ∨ ~q)
≡ p ∨ (q ∧ ~q) … (Distributive Law)
≡ p ∨ F … (Complement Law)
≡ p … (Identity Law)
≡ RHS.

(iii) (p ∧ q) ∨ (~ p ∧ q) ∨ (p ∧ ~q) ≡ p ∨ q
Solution:
LHS = (p ∧ q) v (~p ∧ q) ∨ (p ∧ ~q)
≡ [(p ∨ ~p) ∧ q] ∨ (p ∧ ~q) … (Distributive Law)
≡ (T ∧ q) ∨ (p ∧ ~q) … (Complement Law)
≡ q ∨ (p ∧ ~q) … (Identity Law)
≡ (q ∨ p) ∧ (q ∨ ~q) … (Distributive Law)
≡ (q ∨ p) ∧ T .. (Complement Law)
≡ q ∨ p … (Identity Law)
≡ p ∨ q … (Commutative Law)
≡ RHS.

(iv) ~[(p ∨ ~q) → (p ∧ ~q)] ≡ (p ∨ ~q) ∧ (~p ∨ q)
Solution:
LHS = ~[(p ∨ ~q) → (p ∧ ~q)]
≡ (p ∨ ~q) ∧ ~(p ∧ ~q) … (Negation of implication)
≡ (p ∨ ~q) ∧ [~p ∨ ~(~q)] … (Negation of conjunction)
≡ (p ∨ ~ q) ∧ (~p ∨ q)… (Negation of negation)
≡ RHS.

Ex 1.5

Question 1.
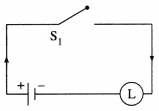
Express the following circuits in the symbolic form of logic and writ the input-output table.
(i)

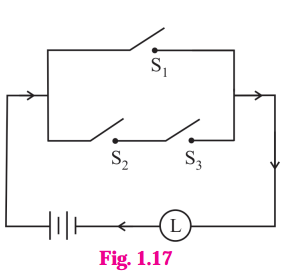
Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~p : the switch S₁‘ is closed or the switch S₁is open
~q : the switch S₂‘ is closed or the switch S₂ is open
~r : the switch S₃‘ is closed or the switch S₃ is open
l : the lamp L is on
(i) The symbolic form of the given circuit is : p ∨ (q ∧ r) = l
l is generally dropped and it can be expressed as : p ∨ (q ∧ r).

(ii)

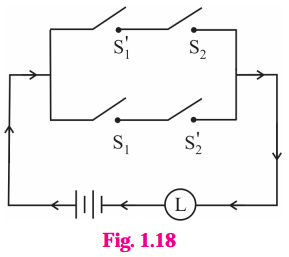
Solution:
The symbolic form of the given circuit is : (~ p ∧ q) ∨ (p ∧ ~ q).

(iii)

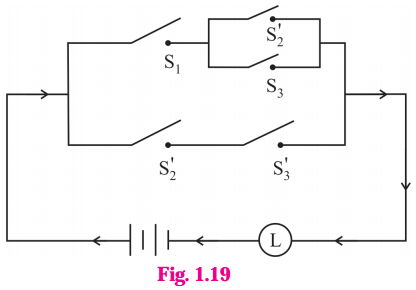
Solution:
The symbolic form of the given circuit is : [p ∧ (~q ∨ r)] ∨ (~q ∧ ~ r).

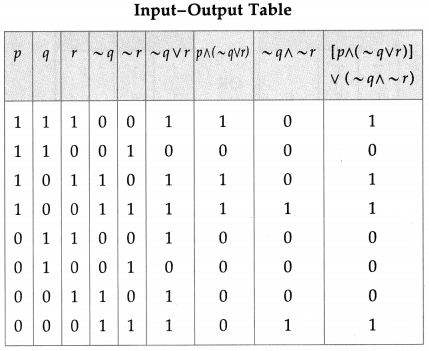
(iv)

Solution:
The symbolic form of the given circuit is : (p ∨ q) ∧ q ∧ (r ∨ ~p).

(v)

Solution:
The symbolic form of the given circuit is : [p ∨ (~p ∧ ~q)] ∨ (p ∧ q).

(vi)

Solution:
The symbolic form of the given circuit is : (p ∨ q) ∧ (q ∨ r) ∧ (r ∨ p)

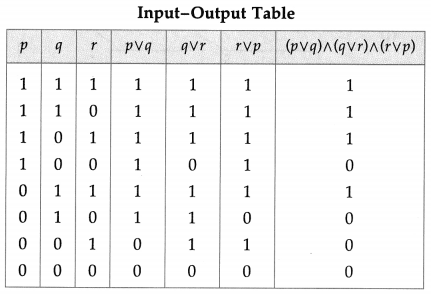
Question 2.
Construct the switching circuit of the following :
(i) (~p∧ q) ∨ (p∧ ~r)
Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open
~ r : the switch S₃‘ is closed or the switch S₃ is open.
Then the switching circuits corresponding to the given statement patterns are :

(ii) (p∧ q) ∨ [~p ∧ (~q ∨ p ∨ r)]
Solution:

(iii) [(p ∧ r) ∨ (~q ∧ ~r)] ∧ (~p ∧ ~r)
Solution:

(iv) (p ∧ ~q ∧ r) ∨ [p ∧ (~q ∨ ~r)]
Solution:

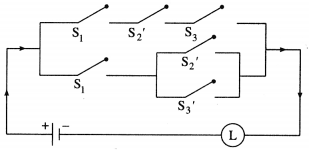
(v) p ∨ (~p ) ∨ (~q) ∨ (p ∧ q)
Solution:

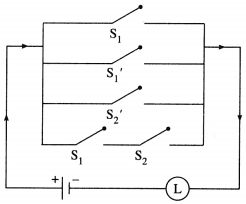
(vi) (p ∧ q) ∨ (~p) ∨ (p ∧ ~q)
Solution:

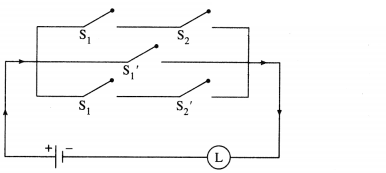
Question 3.
Give an alternative equivalent simple circuits for the following circuits :
(i)

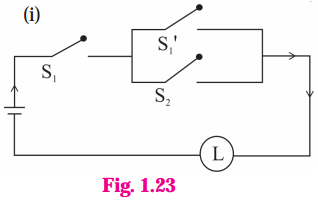
Solution:
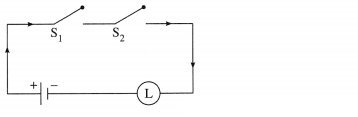
(i) Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p : the switch S₁‘ is closed or the switch Si is open Then the symbolic form of the given circuit is :
p ∧ (~p ∨ q).
Using the laws of logic, we have,
p ∧ (~p ∨ q)
= (p ∧ ~ p) ∨ (p ∧ q) …(By Distributive Law)
= F ∨ (p ∧ q) … (By Complement Law)
= p ∧ q… (By Identity Law)
Hence, the alternative equivalent simple circuit is :

(ii)

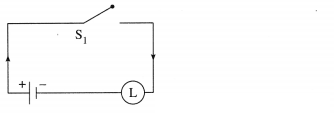
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~q : the switch S₂‘ is closed or the switch S₂ is open
~r : the switch S₃‘ is closed or the switch S₃ is open.
Then the symbolic form of the given circuit is :
[p ∧ (q ∨ r)] ∨ (~r ∧ ~q ∧ p).
Using the laws of logic, we have
[p ∧ (q ∨ r)] ∨ (~r ∧ ~q ∧ p)
≡ [p ∧ (q ∨ r)] ∨ [ ~(r ∨ q) ∧ p] …. (By De Morgan’s Law)
≡ [p ∧ (q ∨ r)] ∨ [p ∧ ~(q ∨ r)] … (By Commutative Law)
≡ p ∧ [(q ∨ r) ∨ ~(q ∨ r)) … (By Distributive Law)
≡ p ∧ T … (By Complement Law)
≡ p … (By Identity Law)
Hence, the alternative equivalent simple circuit is :

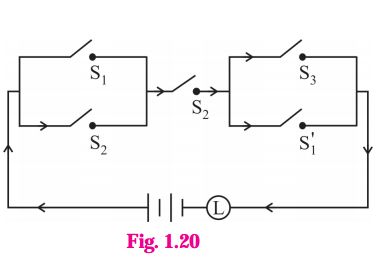
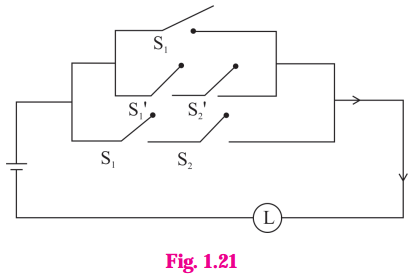
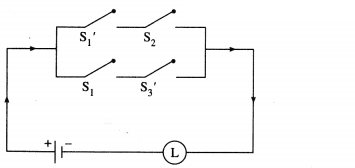
Question 4.
Write the symbolic form of the following switching circuits construct its switching table and interpret it.
i)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form of the given circuit is :
(p ∨ ~q) ∨ (~p ∧ q)

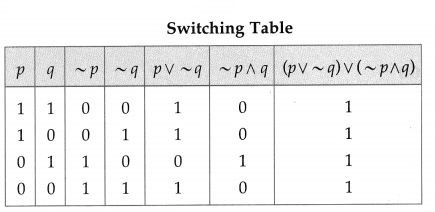
Since the final column contains all’ 1′, the lamp will always glow irrespective of the status of switches.

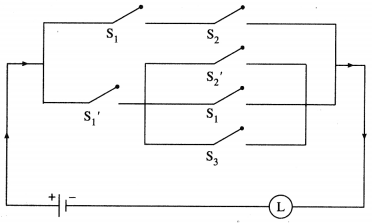
ii)

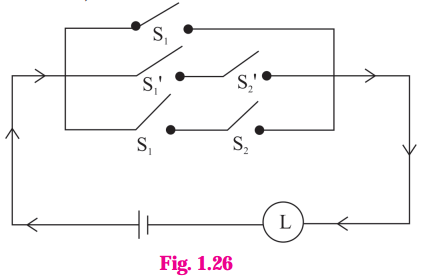
Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~p : the switch S₁ is closed or the switch S₁ is open.
~q : the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form of the given circuit is : p ∨ (~p ∧ ~q) ∨ (p ∧ q)

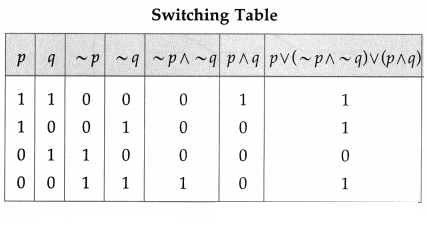
Since the final column contains ‘0’ when p is 0 and q is ‘1’, otherwise it contains ‘1′.
Hence, the lamp will not glow when S₁ is OFF and S₂ is ON, otherwise the lamp will glow.

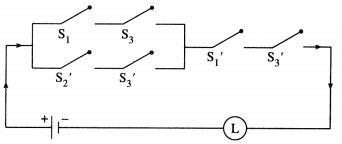
iii)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~q : the switch S₂‘ is closed or the switch S₂ is open
~r: the switch S₃‘ is closed or the switch S₃ is open.
Then the symbolic form of the given circuit is : [p ∨ (~q) ∨ r)] ∧ [p ∨ (q ∧ r)]

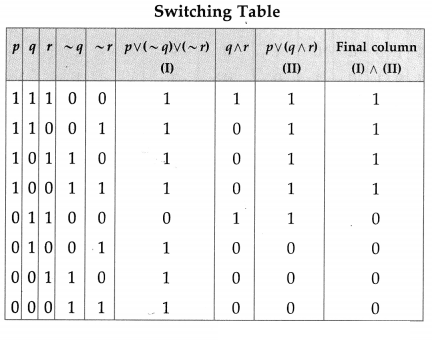
From the switching table, the ‘final column’ and the column of p are identical. Hence, the lamp will glow which S₁ is ‘ON’.

Question 5.
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
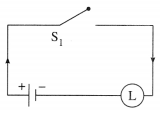
(i) p ∨ (q ∧ ~ q)
Solution:
Using the laws of logic, we have, p ∨ (q ∧ ~q)
≡ p ∨ F … (By Complement Law)
≡ p … (By Identity Law)
Hence, the simple logical expression of the given expression is p.
Let p : the switch S₁ is closed
Then the corresponding switching circuit is :

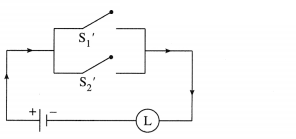
(ii) (~p ∧ q) ∨ (~p ∧ ~q) ∨ (p ∧ ~q)]
Solution:
Using the laws of logic, we have,
(~p ∧ q) ∨ (~p ∨ ~q) ∨ (p ∧ ~q)
≡ [~p ∧ (q ∨ ~q)] ∨ (p ∧ ~ q)… (By Distributive Law)
≡ (~p ∧ T) ∨ (p ∧ ~q) … (By Complement Law)
≡ ~p ∨ (p ∧ ~q) … (By Identity Law)
≡ (~p ∨ p) ∧ (~p ∧~q) … (By Distributive Law)
≡ T ∧ (~p ∧ ~q) … (By Complement Law)
≡ ~p ∨ ~q … (By Identity Law)
Hence, the simple logical expression of the given expression is ~ p ∨ ~q.
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open,
Then the corresponding switching circuit is :

(iii) [p (∨ (~q) ∨ ~r)] ∧ (p ∨ (q ∧ r)
Solution:
Using the laws of logic, we have,
[p ∨ (~ (q) ∨ (~r)] ∧ [p ∨ (q ∧ r)]
= [p ∨ { ~(q ∧ r)}] ∧ [p ∨ (q ∧ r)] … (By De Morgan’s Law)
= p ∨ [~(q ∧ r) ∧ (q ∧ r) ] … (By Distributive Law)
= p ∨ F … (By Complement Law)
= p … (By Identity Law)
Hence, the simple logical expression of the given expression is p.
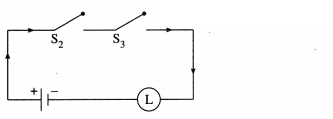
Let p : the switch S₁ is closed
Then the corresponding switching circuit is :

(iv) (p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) ∨ (p ∧ q ∧ r)
Question is Modified
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r)∨ (p ∧ q ∧ r)
Solution:
Using the laws of logic, we have,
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r)
= (p ∧ ~p ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Commutative Law)
= (F ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Complement Law)
= F ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Identity Law)
= (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Identity Law)
= (~ p ∨ p) ∧ (q ∧ r) … (By Distributive Law)
= T ∧ (q ∧ r) … (By Complement Law)
= q ∧ r … (By Identity Law)
Hence, the simple logical expression of the given expression is q ∧ r.
Let q : the switch S₂ is closed
r : the switch S₃ is closed.
Then the corresponding switching circuit is :

Download PDF

Maharashtra Board Solutions Class 12 Maths (Part 1): Chapter 1- Mathematical Logic

Download PDF: Maharashtra Board Solutions Class 12 Maths (Part 1): Chapter 1- Mathematical Logic PDF

Chapterwise Maharashtra Board Solutions Class 12 Arts & Science Maths (Part 1) :

• Chapter 1- Mathematical Logic
• Chapter 2- Matrices
• Chapter 3- Trigonometric Functions
• Chapter 4- Pair of Straight Lines
• Chapter 5- Vectors
• Chapter 6- Line and Plane
• Chapter 7- Linear Programming

FAQs

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC. 

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.

Read More

• RD Sharma Solutions for Class 11 Maths Chapter 31–Mathematical Reasoning
• NCERT Solutions for 7th Class Science: Chapter 14-Electric Current and its Effect
• NCERT Solutions for 6th Class Science: Chapter 12-Electricity and Circuits
• Maharashtra Board Solutions Class 12 Chemistry: Chapter 5- Electrochemistry
• Rosary Matriculation Higher Secondary School

IndCareer Board Book Solutions App

IndCareer Board Book App provides complete study materials for students from classes 1 to 12 of Board. The App contains complete solutions of NCERT books, notes, and other important materials for students. Download the IndCareer Board Book Solutions now.