Maharashtra Board Solutions Class 11-Arts & Science Maths (Part 2): Chapter 3- Permutations and Combination

Class 11: Maths Chapter 3 solutions. Complete Class 11 Maths Chapter 3 Notes.

Maharashtra Board Solutions Class 11-Arts & Science Maths (Part 2): Chapter 3- Permutations and Combination

Maharashtra Board 11th Maths Chapter 3, Class 11 Maths Chapter 3 solutions

Ex 3.1

Question 1.
A teacher wants to select the class monitor in a class of 30 boys and 20 girls. In how many ways can the monitor be selected if the monitor must be a girl?
Solution:
There are 30 boys and 20 girls.
A teacher can select any boy as a class monitor from 30 boys in 30 different ways and he can select any girl as a class monitor from 20 girls in 20 different ways.
∴ by the fundamental principle of addition, the total number of ways a teacher can select a class monitor = 30 + 20 = 50
Hence, there are 50 different ways to select a class monitor.

Question 2.
A Signal is generated from 2 flags by putting one flag above the other. If 4 flags of different colours are available, how many different signals can be generated?
Solution:
A signal is generated from 2 flags and there are 4 flags of different colours available.
∴ 1st flag can be any one of the available 4 flags.
∴ It can be selected in 4 ways.
Now, 2nd flag is to be selected for which 3 flags are available for a different signal.
∴ 2nd flag can be anyone from these 3 flags.
∴ It can be selected in 3 ways.
∴ By using the fundamental principle of multiplication, total no. of ways a signal can be generated = 4 × 3 = 12
∴ 12 different signals can be generated.

Question 3.
How many two-letter words can be formed using letters from the word SPACE, when repetition of letters (i) is allowed (ii) is not allowed
Solution:
A two-letter word is to be formed out of the letters of the word SPACE.
(i) When repetition of the letters is allowed 1st letter can be selected in 5 ways.
2nd letter can be selected in 5 ways.
∴ By using the fundamental principle of multiplication, the total number of 2-letter words = 5 × 5 = 25

(ii) When repetition of the letters is not allowed 1st letter can be selected in 5 ways.
2nd letter can be selected in 4 ways.
∴ By using the fundamental principle of multiplication, the total number of 2-letter words = 5 × 4 = 20

Question 4.
How many three-digit numbers can be formed from the digits 0, 1, 3, 5, 6 if repetitions of digits (i) are allowed (ii) are not allowed?
Solution:
A three-digit number is to be formed from the digits 0, 1, 3, 5, 6.
(i) When repetition of digits is allowed,
100’s place digit should be a non-zero number.
Hence, it can be anyone from digits 1, 3, 5,6.
∴ 100’s place digit can be selected in 4 ways.
10’s and unit’s place digit can be zero and digits can be repeated.
∴ 10’s place digit can be selected in 5 ways and the unit’s place digit can be selected in 5 ways.
∴ By using the fundamental principle of multiplication, the total number of three-digit numbers = 4 × 5 × 5 = 100

(ii) When repetition of digits is not allowed,
100’s place digit should be a non-zero number.
Hence, it can be anyone from digits 1, 3, 5, 6.
∴ 100’s place digit can be selected in 4 ways.
10’s and unit’s place digit can be zero and digits can’t be repeated.
∴ 10’s place digit can be selected in 4 ways and the unit’s place digit can be selected in 3 ways.
∴ By using the fundamental principle of multiplication, the total number of two-digit numbers = 4 × 4 × 3 = 48

Question 5.
How many three-digit numbers can be formed using the digits 2, 3, 4, 5, 6 if digits can be repeated?
Solution:
A 3-digit number is to be formed from the digits 2, 3, 4, 5, 6 where digits can be repeated.
∴ Unit’s place digit can be selected in 5 ways.
10’s place digit can be selected in 5 ways.
100’s place digit can be selected in 5 ways.
∴ By using fundamental principle of multiplication, total number of 3-digit numbers = 5 × 5 × 5 = 125

Question 6.
A letter lock contains 3 rings and each ring contains 5 letters. Determine the maximum number of false trails that can be made before the lock is opened.
Solution:
A letter lock has 3 rings, each ring containing 5 different letters.
∴ A letter from each ring can be selected in 5 ways.
∴ By using the fundamental principle of multiplication, a total number of trials that can be made = 5 × 5 × 5 = 125.
Out of these 124 wrong attempts are made and in the 125th attempt, the lock gets opened.
∴ A maximum number of false trials = 124.

Question 7.
In a test, 5 questions are of the form ‘state, true or false. No student has got all answers correct. Also, the answer of every student is different. Find the number of students who appeared for the test.
Solution:
Every question can be answered in 2 ways. (True or False)
∴ By using the fundamental principle of multiplication, the total number of set of answers possible = 2 × 2 × 2 × 2 × 2 = 32.
Since One of them is the case where all questions are answered correctly,
The number of wrong answers = 32 – 1 = 31.
Since no student has answered all the questions correctly, the number of students who appeared for the test are 31.

Question 8.
How many numbers between 100 and 1000 have 4 in the unit’s place?
Solution:
Numbers between 100 and 1000 are 3-digit numbers.
A 3-digit number is to be formed from the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, where the unit place digit is 4.
Unit’s place digit is 4.
∴ it can be selected in 1 way only.
10’s place digit can be selected in 10 ways.
For a 3-digit number, 100’s place digit should be a non-zero number.
∴ 100’s place digit can be selected in 9 ways.
∴ By using the fundamental principle of multiplication,
total numbers between 100 and 1000 which have 4 in the units place = 1 × 10 × 9 = 90.

Question 9.
How many numbers between 100 and 1000 have the digit 7 exactly once?
Solution:
Numbers between 100 and 1000 are 3-digit numbers.
A 3-digit number is to be formed from the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, where exactly one of the digits is 7.
When 7 is in unit’s place:
Unit’s place digit is 7.
∴ it can be selected in 1 way only.
10’s place digit can be selected in 9 ways.
100’s place digit can be selected in 8 ways.
Total numbers which have 7 in unit’s place = 1 × 9 × 8 = 72.

When 7 is in 10’s place:
Unit’s place digit can be selected in 9 ways.
10’s place digit is 7.
∴ it can be selected in 1 way only.
100’s place digit can be selected in 8 ways.
∴ A total number of numbers which have 7 in 10’s place = 9 × 1 × 8 = 72.

When 7 is in 100’s place:
Unit’s place digit can be selected in 9 ways.
10’s place digit can be selected in 9 ways.
100’s place digit is 7.
∴ it can be selected in 1 way only.
∴ Total numbers which have 7 in 100’s place = 9 × 9 × 1 = 81.
∴ Total numbers between 100 and 1000 having digit 7 exactly once = 72 + 72 + 81 = 225

Question 10.
How many four-digit numbers will not exceed 7432 if they are formed using the digits 2, 3, 4, 7 without repetition?
Solution:
Between any set of digits, the greatest number is possible when digits are arranged in descending order.
∴ 7432 is the greatest number, formed from the digits 2, 3, 4, 7.
Since a 4-digit number is to be formed from the digits 2, 3, 4, 7, where repetition of the digit is not allowed,
1000’s place digit can be selected in 4 ways,
100’s place digit can be selected in 3 ways,
10’s place digit can be selected in 2 ways,
Unit’s place digit can be selected in 1 way.
∴ Total number of numbers not exceeding 7432 that can be formed with the digits 2, 3, 4, 7 = Total number of four-digit numbers possible from the digits 2, 3, 4, 7
= 4 × 3 × 2 × 1
= 24

Question 11.
If numbers are formed using digits 2, 3, 4, 5, 6 without repetition, how many of them will exceed 400?
Solution:
Case I: Number of three-digit numbers formed from 2, 3, 4, 5, 6, greater than 400.
100’s place can be filled by any one of the numbers 4, 5, 6.
100’s place digit can be selected in 3 ways.
Since repetition is not allowed, 10’s place can be filled by any one of the remaining four numbers.
∴ 10’s place digit can be selected in 4 ways.
Unit’s place digit can be selected in 3 ways.
∴ Total number of three-digit numbers formed = 3 × 4 × 3 = 36

Case II: Number of four-digit numbers formed from 2, 3, 4, 5, 6.
Since repetition of digits is not allowed,
1000’s place digit can be selected in 5 ways.
100’s place digit can be selected in 4 ways.
10’s place digit can be selected in 3 ways.
Unit’s place digit can be selected in 2 ways.
∴ Total number of four-digit numbers formed = 5 × 4 × 3 × 2 = 120

Case III: Number of five-digit numbers formed from 2, 3, 4, 5, 6.
Similarly, since repetition of digits is not allowed,
Total number of five digit numbers formed = 5 × 4 × 3 × 2 × 1 = 120.
∴ Total number of numbers that exceed 400 = 36 + 120 + 120 = 276

Question 12.
How many numbers formed with the digits 0, 1, 2, 5, 7, 8 will fall between 13 and 1000 if digits can be repeated?
Solution:
Case I: 2-digit numbers more than 13, less than 20, formed from the digits 0, 1, 2, 5, 7, 8.
10’s place digit is 1.
∴ it can be selected in 1 way only.
Unit’s place can be filled by any one of the numbers 5, 7, 8.
∴ Unit’s place digit can be selected in 3 ways.
∴ Total number of such numbers = 1 × 3 = 3.

Case II: 2-digit numbers more than 20 formed from 0, 1, 2, 5, 7, 8.
10’s place can be filled by any one of the numbers 2, 5, 7, 8.
∴ 10’s place digit can be selected in 4 ways.
Since repetition is allowed, the unit’s place can be filled by one of the remaining 6 digits.
∴ Unit’s place digit can be selected in 6 ways.
∴ Total number of such numbers = 4 × 6 = 24.

Case III: 3-digit numbers formed from 0, 1, 2, 5, 7, 8.
Similarly, since repetition of digits is allowed, the total number of such numbers = 5 × 6 × 6 = 180.
All cases are mutually exclusive.
∴ Total number of required numbers = 3 + 24 + 180 = 207

Question 13.
A school has three gates and four staircases from the first floor to the second floor. How many ways does a student have to go from outside the school to his classroom on the second floor?
Solution:
A student can go inside the school from outside in 3 ways and from the first floor to the second floor in 4 ways.
∴ A number of ways to choose gates = 3.
The number of ways to choose a staircase = 4.
By using the fundamental principle of multiplication,
number of ways in which a student has to go from outside the school to his classroom = 4 × 3 = 12

Question 14.
How many five-digit numbers formed using the digit 0, 1, 2, 3, 4, 5 are divisible by 5 if digits are not repeated?
Solution:
Here, repetition of digits is not allowed.
For a number to be divisible by 5,
unit’s place digit should be 0 or 5.
Case I: when unit’s place is 0
Unit’s place digit can be selected in 1 way.
10’s place digit can be selected in 5 ways.
100’s place digit can be selected in 4 ways.
1000’s place digit can be selected in 3 ways.
10000’s place digit can be selected in 2 ways.
∴ Total number of numbers = 1 × 5 × 4 × 3 × 2 = 120.

Case II: when the unit’s place is 5
Unit’s place digit can be selected in 1 way.
10000’s place should be a non-zero number.
∴ It can be selected in 4 ways.
1000’s place digit can be selected in 4 ways.
100’s place digit can be selected in 3 ways.
10’s place digit can be selected in 2 ways.
∴ Total number of numbers = 1 × 4 × 4 × 3 × 2 = 96
∴ Total number of required numbers = 120 + 96 = 216

Ex 3.2

Question 1.
Evaluate:
(i) 8!
Solution:
8!
= 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 40320

(ii) 10!
Solution:
10!
= 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 3628800

(iii) 10! – 6!
Solution:
10! – 6!
= 10 × 9 × 8 × 7 × 6! – 6!
= 6! (10 × 9 × 8 × 7 – 1)
= 6! (5040 – 1)
= 6 × 5 × 4 × 3 × 2 × 1 × 5039
= 3628080

(iv) (10 – 6)!
Solution:
(10 – 6)!
= 4!
= 4 × 3 × 2 × 1
= 24

Question 2.
Compute:
(i) 12!6!
Solution:
12!6!=12×11×10×9×8×7×6!6!
= 12 × 11 × 10 × 9 × 8 × 7
= 665280

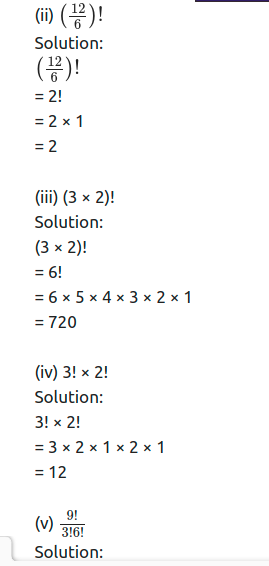
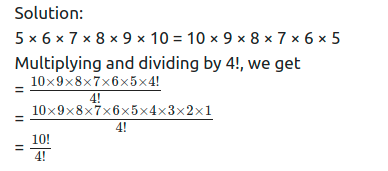
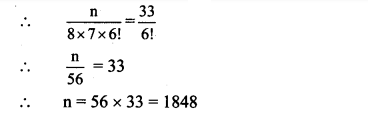
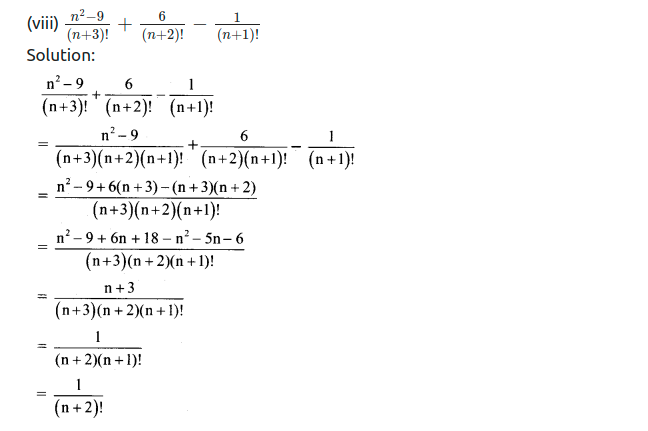
Ex 3.3

Question 1.
Find n, if ⁿP₆ : ⁿP₃ = 120 : 1.
Solution:
ⁿP₆ : ⁿP₃ = 120 : 1

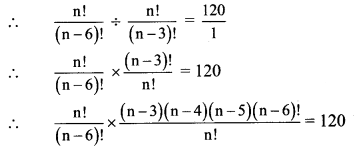
∴ (n – 3) (n – 4) (n – 5) = 120
∴ (n – 3) (n – 4) (n – 5) = 6 × 5 × 4
Comparing on both sides, we get
n – 3 = 6
∴ n = 9

Question 2.
Find m and n, if ^(m+n)P₂ = 56 and ^(m-n)P₂ = 12.
Solution:
^(m+n)P₂ = 56

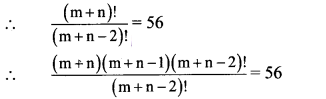
(m + n) (m + n – 1) = 56
Let m + n = t
t(t – 1) = 56
t² – t – 56 = 0
(t – 8) (t + 7) = 0
t = 8 or t = -7
m + n = 8 or m + n = -7
But m + n ≠ -7
∴ m + n = 8 ……(i)
Also, ^(m-n)P₂ = 12

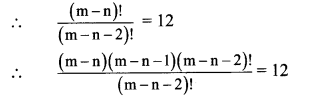
(m – n) (m – n – 1) = 12
Let m – n = a
a(a – 1) = 12
a² – a – 12 = 0
(a – 4)(a + 3) = 0
a = 4 or a = -3
m – n = 4 or m – n = -3
But m – n ≠ -3
∴ m – n = 4 ……(ii)
Adding (i) and (ii), we get
2m = 12
∴ m = 6
Substituting m = 6 in (ii), we get
6 – n = 4
∴ n = 2

Question 3.
Find r, if ¹²P_r-2 : ¹¹P_r-1 = 3 : 14.
Solution:

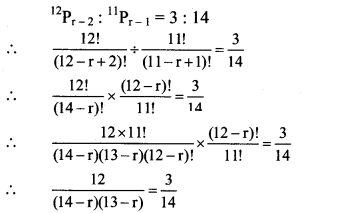
(14 – r)(13 – r) = 8 × 7
Comparing on both sides, we get
14 – r = 8
∴ r = 6

Question 4.
Show that (n + 1) (ⁿP_r) = (n – r + 1) [⁽ⁿ⁺¹⁾P_r]
Solution:

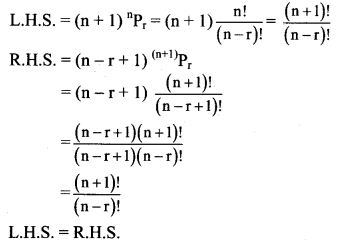
Question 5.
How many 4 letter words can be formed using letters in the word MADHURI, if (a) letters can be repeated (b) letters cannot be repeated.
Solution:
There are 7 letters in the word MADHURI.
(a) A 4 letter word is to be formed from the letters of the word MADHURI and repetition of letters is allowed.
∴ 1st letter can be filled in 7 ways.
2nd letter can be filled in 7 ways.
3rd letter can be filled in 7 ways.
4th letter can be filled in 7 ways.
∴ Total no. of ways a 4-letter word can be formed = 7 × 7 × 7 × 7 = 2401

for the principal and if no two girls are together, find the number of arrangements.
Solution:
In 1st row, 6 teachers can be arranged among themselves in ⁶P₆ = 6! ways.
In the 2nd row, 12 boys can be arranged among themselves in ¹²P₁₂ = 12! ways.
No two girls are together.
So, there are 13 places formed by 12 boys in which 6 girls occupy any 6 places in ¹³P₆ ways.
∴ Required number of arrangements

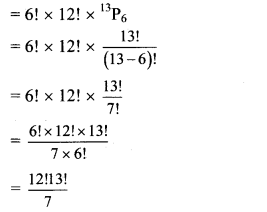
Question 8.
Find the number of ways so that letters of the word HISTORY can be arranged as
(a) Y and T are together
(b) Y is next to T
(c) there is no restriction
(d) begin and end with a vowel
(e) end in ST
(f) begin with S and end with T
Solution:
There are 7 letters in the word HISTORY
(a) When ‘Y’ and ‘T’ are together.
Let us consider ‘Y’ and ‘T’ as one unit.
This unit with other 5 letters are to be arranged.
∴ The number of arrangement of one unit and 5 letters = ⁶P₆ = 6! = 720
Also, ‘Y’ and ‘T’ can be arranged among themselves in ²P₂ = 2! = 2 ways.
∴ A total number of arrangements when Y and T are always together = 6! × 2!
= 120 × 2
= 1440

(b) When ‘Y’ is next to ‘T’.
Let us take this (‘Y’ next to ‘T’) as one unit.
This unit with 5 other letters is to be arranged.
∴ The number of arrangements of 5 letters and one unit = ⁶P₆ = 6! = 720
Also, ‘Y’ has to be always next to ‘T’.
∴ They can be arranged among themselves in 1 way only.
∴ Total number of arrangements possible when Y is next to T = 720 × 1 = 720

(c) When there is no restriction.
7 letters can be arranged among themselves in ⁷P₇ = 7! ways.
∴ The total number of arrangements possible if there is no restriction = 7!

(d) When begin and end with a vowel.
There are 2 vowels in the word HISTORY.
All other letters of the word HISTORY are to be arranged between 2 vowels such that the arrangement begins and ends with a vowel.
The other 5 letters can be filled between the two vowels in ⁵P₅ = 5! = 120 ways.
Also, 2 vowels can be arranged among themselves at first and last places in ²P₂ = 2! = 2 ways.
∴ Total number of arrangements when the word begins and ends with vowel = 120 × 2 = 240

(e) When a word ends in ST.
As the arrangement ends with ST,
the remaining 5 letters can be arranged among themselves in ⁵P₅ = 5! = 120 ways.
∴ Total number of arrangements when the word ends with ST = 120

(f) When a word begins with S and ends with T.
As arrangement begins with S and ends with T,
the remaining 5 letters can be arranged between S and T among themselves in ⁵P₅ = 5! = 120 ways.
Total number of arrangements when the word begins with S and ends with T = 120

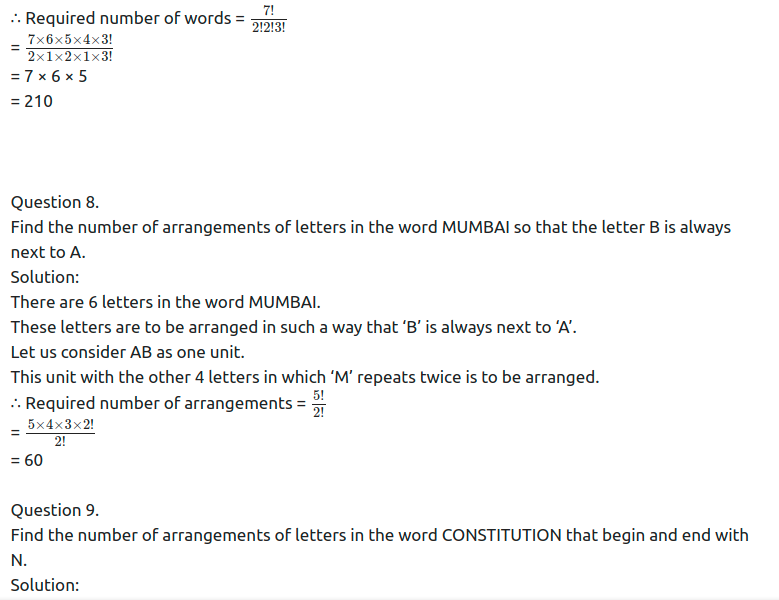
Question 9.
Find the number of arrangements of the letters in the word SOLAPUR so that consonants and vowels are placed alternately.
Solution:
There are 4 consonants S, L, P, R, and 3 vowels A, O, U in the word SOLAPUR.
Consonants and vowels are to be alternated.
∴ Vowels must occur in even places and consonants in odd places.
∴ 3 vowels can be arranged at 3 even places in ³P₃ = 3! = 6 ways.
Also, 4 consonants can be arranged at 4 odd places in ⁴P₄ = 4! = 24 ways.
Required number of arrangements = 6 × 24 = 144

Question 10.
Find the number of 4-digit numbers that can be formed using the digits 1, 2, 4, 5, 6, 8 if
(a) digits can be repeated.
(b) digits cannot be repeated.
Solution:
(a) A 4 digit number is to be made from the digits 1, 2, 4, 5, 6, 8 such that digits can be repeated.
∴ Unit’s place digit can be filled in 6 ways.
10’s place digit can be filled in 6 ways.
100’s place digit can be filled in 6 ways.
1000’s place digit can be filled in 6 ways.
∴ Total number of numbers that can be formed = 6 × 6 × 6 × 6 = 1296

(b) A 4 different digit number is to be made from the digits 1, 2, 4, 5, 6, 8 without repetition of digits.
∴ 4 different digits are to be arranged from 6 given digits which can be done in ⁶P₄ ways.
∴ Total number of numbers that can be formed

The other 5 digits can be arranged among themselves in ⁵P₅ = 5! = 120 ways.
∴ Required number of numbers divisible by 5 = 1 × 120 = 120

(b) If the number is not divisible by 5,
unit’s place can be any digit from 3, 4, 6, 7, 8.
∴ it can be arranged in 5 ways.
Other 5 digits can be arranged in ⁵P₅ = 5! = 120 ways.
∴ Required number of numbers not divisible by 5 = 5 × 120 = 600

Question 13.
A code word is formed by two different English letters followed by two non-zero distinct digits. Find the number of such code words. Also, find the number of such code words that end with an even digit.
Solution:
There is a total of 26 alphabets.
A code word contains 2 English alphabets.
∴ 2 alphabets can be filled in ²⁶P₂

Question 16.
In how many ways can 5 different books be arranged on a shelf if
(i) there are no restrictions
(ii) 2 books are always together
(iii) 2 books are never together
Solution:
(i) 5 books arranged in ⁵P₅ = 5! = 120 ways.

(ii) 2 books are together.
Let us consider two books as one unit. This unit with the other 3 books can be arranged in ⁴P₄ = 4! = 24 ways.
Also, two books can be arranged among themselves in ²P₂ = 2 ways.
∴ Required number of arrangements = 24 × 2 = 48

(iii) Say books are B₁, B₂, B₃, B₄, B₅ are to be arranged with B₁, B₂ never together.
B₃, B₄, B₅ can be arranged among themselves in ³P₃ = 3! = 6 ways.
B₃, B₄, B₅ create 4 gaps in which B₁, B₂ are arranged in ⁴P₂ = 4 × 3 = 12 ways.
∴ Required number of arrangements = 6 × 12 = 72

Question 17.
3 boys and 3 girls are to sit in a row. How many ways can this be done if
(i) there are no restrictions.
(ii) there is a girl at each end.
(iii) boys and girls are at alternate places.
(iv) all-boys sit together.
Solution:
3 boys and 3 girls are to be arranged in a row.
(i) When there are no restrictions.
∴ Required number of arrangements = 6! = 720

(ii) When there is a girl at each end.
3 girls can be arranged at two ends in
³P₂ = 3!1! = 3 × 2 = 6 ways.
And remaining 1 girl and 3 boys can be arranged between the two girls in ⁴P₄ = 4! = 24 ways.
∴ Required number of arrangements = 6 × 24 = 144

(iii) Boys and girls are at alternate places.
We can first arrange 3 girls among themselves in ³P₃ = 3! = 6 ways.
Let girls be denoted by G.
G – G – G –
There are 3 places marked by ‘-’ where 3 boys can be arranged in 3! = 6 ways.
∴ Total number of such arrangements = 6 × 6 = 36
OR
Similarly, we can first arrange 3 boys in 3! = 6 ways
and then arrange 3 girls alternately in 3! = 6 ways.
∴ Total number of such arrangements = 6 × 6 = 36
∴ Required number of arrangements = 36 + 36 = 72

(iv) All boys sit together.
Let us consider all boys as one group.
This one group with the other 3 girls can be arranged ⁴P₄ = 4! = 24 ways.
Also, 3 boys can be arranged among themselves in ³P₃ = 3! = 6 ways.
∴ Required number of arrangements = 24 × 6 = 144

Ex 3.4

Question 1.
Find the number of permutations of letters in each of the following words.
(i) DIVYA
(ii) SHANTARAM
(iii) REPRESENT
(iv) COMBINE
(v) BAL BHARATI
Solution:
(i) There are 5 distinct letters in the word DIVYA.
∴ Number of permutations of the letters of the word DIVYA = 5! = 120

(ii) There are 9 letters in the word SHANTARAM in which ‘A’ is repeated 3 times.
∴ Number of permutations of the letters of the word SHANTARAM = 9!3!
= 9 × 8 × 7 × 6 × 5 × 4
= 60480

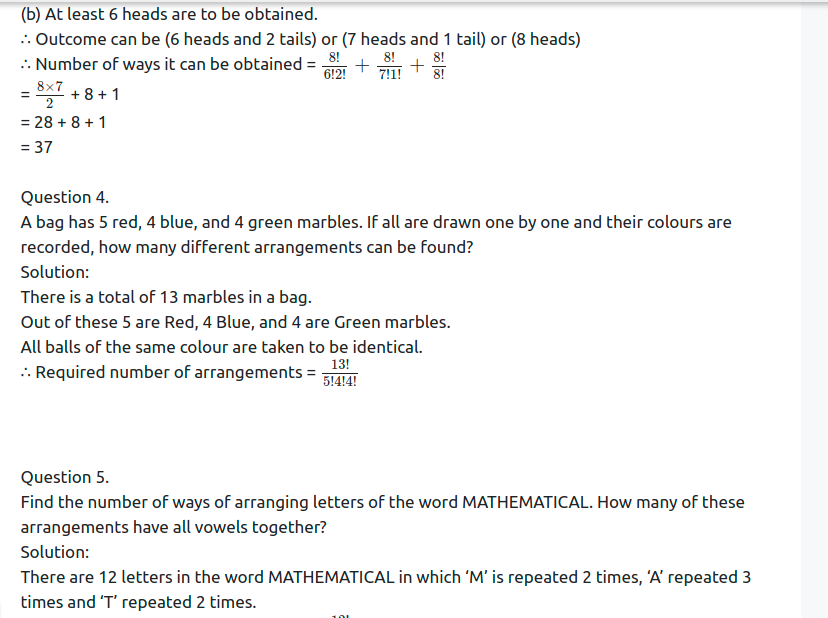
There are 12 letters in the word CONSTITUTION, in which ‘O’, ‘N’, ‘I’ repeat two times each, ‘T’ repeats 3 times.
When the arrangement starts and ends with ‘N’,
other 10 letters can be arranged between two N,
in which ‘O’ and ‘I’ repeat twice each and ‘T’ repeats 3 times.
∴ Required number of arrangements = 10!2!2!3!

As the digit 9 repeats twice in the remaining four numbers, the number of arrangements = 4!2! = 12
∴ 6-digit numbers that are divisible by 4 so formed are 12 + 12 + 12 + 12 = 48.
Case II: When the last two digits are 92 or 96.
As each of the remaining four numbers are distinct, the number of arrangements = 4! = 24
∴ 6-digit numbers that are divisible by 4 so formed are 24 + 24 = 48.
∴ Required number of numbers framed = 48 + 48 = 96

Ex .3.5

Question 1.
In how many different ways can 8 friends sit around a table?
Solution:
We know that ‘n’ persons can sit around a table in (n – 1)! ways.
∴ 8 friends can sit around a table in 7!
= 7 × 6 × 5 × 4 × 3 × 2 × 1
= 5040 ways.

Question 2.
A party has 20 participants. Find the number of distinct ways for the host to sit with them around a circular table. How many of these ways have two specified persons on either side of the host?
Solution:
A party has 20 participants.
All of them and the host (i.e., 21 persons) can be seated at a circular table in (21 – 1)! = 20! ways.
When two particular participants are seated on either side of the host.
The host takes the chair in 1 way.
These 2 persons can sit on either side of the host in 2! ways.
Once the host occupies his chair, it is not circular permutation more.
The remaining 18 people occupy their chairs in 18! ways.
∴ A total number of arrangements possible if two particular participants are seated on either side of the host = 2! × 18! = 2 × 18!

Question 3.
Delegates from 24 countries participate in a round table discussion. Find the number of seating arrangements where two specified delegates are (a) always together. (b) never together.
Solution:
(a) Delegates of 24 countries are to participate in a round table discussion such that two specified delegates are always together.
Let us consider these 2 delegates as one unit. They can be arranged among themselves in 2! ways.
Also, these two delegates are to be seated with 22 other delegates (i.e. total of 23) which can be done in (23 – 1)! = 22! ways.
∴ Required number of arrangements = 2! × 22!

(b) When 2 specified delegates are never together then, other 22 delegates can be participate in a round table discussion in (22 – 1)! = 21! ways.
∴ There are 22 places of which any 2 places can be filled by those 2 delegates so that they are never together.
∴ Two specified delegates can be arranged in ²²P₂ ways.
∴ Required number of arrangements = ²²P₂ × 21!

Question 4.
Find the number of ways for 15 people to sit around the table so that no two arrangements have the same neighbours.
Solution:
There are 15 people to sit around a table.
∴ They can be arranged in(15 – 1)! = 14! ways.
But, they should not have the same neighbour in any two arrangements.
Around the table, arrangements (i.e., clockwise and anticlockwise) coincide.

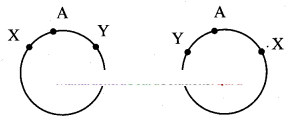
∴ Required number of arrangements = 14!2

Question 5.
A committee of 10 members sits around a table. Find the number of arrangements that have the President and the Vice-president together.
Solution:
A committee of 10 members sits around a table.
But, President and Vice-president sit together.
Let us consider President and Vice-president as one unit.
They can be arranged among themselves in 2! ways.
Now, this unit with the other 8 members of the committee is to be arranged around a table, which can be done in (9 – 1)! = 8! ways.
∴ Required number of arrangements = 8! × 2! = 2 × 8!

Question 6.
Five men, two women, and a child sit around a table. Find the number of arrangements where the child is seated (a) between the two women. (b) between two men.
Solution:
5 men, 2 women, and a child sit around a table.
(a) When the child is seated between two women.
5 men, 2 women, and a child are to be seated around a round table such that the child is seated between two women.
∴ the two women can be seated on either side of the child in 2! ways.
Let us consider these 3 (two women and a child) as one unit.
Now, this one unit is to be arranged with the remaining 5 men,
i.e., a total of 6 units are to be arranged around a round table, which can be done in (6 – 1)! = 5! ways.
∴ Required number of arrangements = 5! × 2!
= 120 × 2
= 240

Ex 3.6

Question 1.
Find the value of
(a) ¹⁵C₄
Solution:

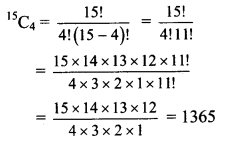
(b) ⁸⁰C₂
Solution:

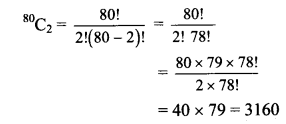
(c) ¹⁵C₄ + ¹⁵C₅
Solution:

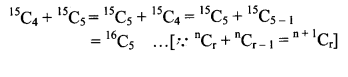
(d) ²⁰C₁₆ – ¹⁹C₁₆
Solution:

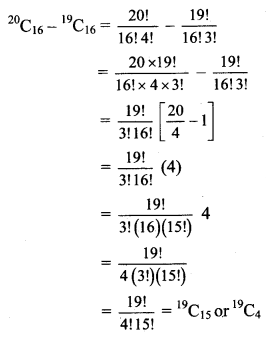
Question 2.
Find n if
(a) ⁶P₂ = n(⁶C₂)
Solution:

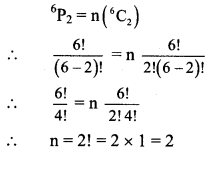
(b) ²ⁿC₃ : ⁿC₂ = 52 : 3
Solution:

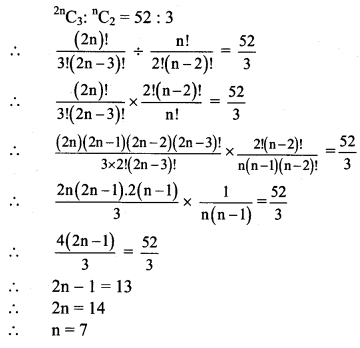
(c) ⁿC_n-3 = 84
Solution:

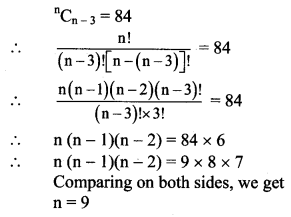
Question 3.
Find r if ¹⁴C_2r : ¹⁰C_2r-4 = 143 : 10.
Solution:

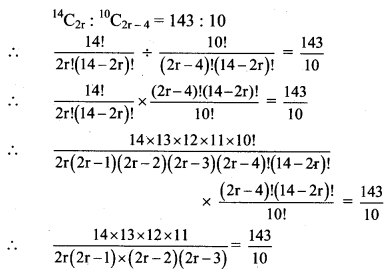
∴ 2r(2r – 1) (2r – 2) (2r – 3) = 14 × 12 × 10
∴ 2r(2r – 1) (2r – 2) (2r – 3) = 8 × 7 × 6 × 5
Comparing on both sides, we get
∴ r = 4

Question 4.
Find n and r if,
(a) ⁿP_r = 720 and ⁿC_n-r = 120
Solution:

(b) ⁿC_r-1 : ⁿC_r : ⁿC_r+1 = 20 : 35 : 42
Solution:

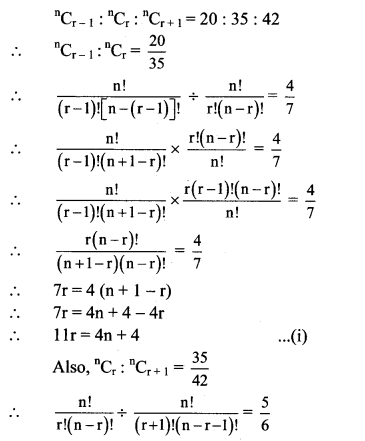
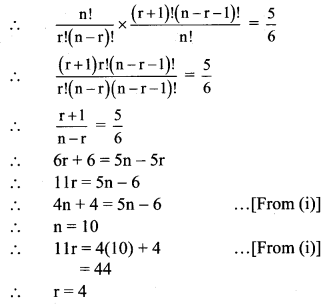
Question 5.
If ⁿP_r = 1814400 and ⁿC_r = 45, find ⁿ⁺⁴C_r+3.
Solution:

Question 6.
If ⁿC_r-1 = 6435, ⁿC_r = 5005, ⁿC_r+1 = 3003, find ^rC₅.
Solution:

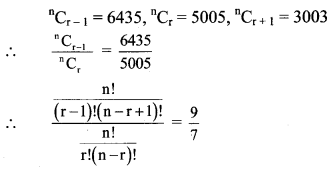
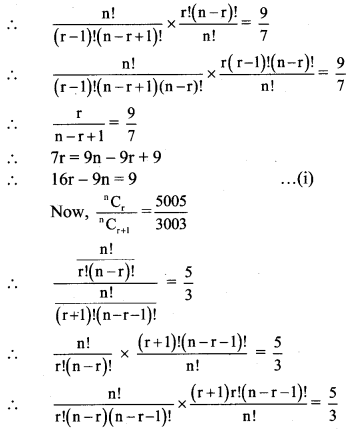
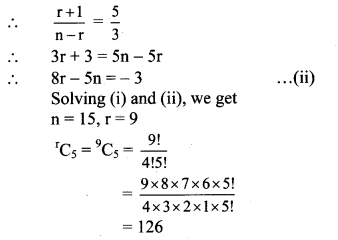
Question 7.
Find the number of ways of drawing 9 balls from a bag that has 6 red balls, 8 green balls, and 7 blue balls so that 3 balls of every colour are drawn.
Solution:
9 balls are to be selected from 6 red, 8 green, 7 blue balls such that the selection consists of 3 balls of each colour.
∴ 3 red balls can be selected from 6 red balls in ⁶C₃ ways.
3 reen balls can be selected from 8 green balls in ⁸C₃ ways.
3 blue balls can be selected from 7 blue balls in ⁷C₃ ways.
∴ Number of ways selection can be done if the selection consists of 3 balls of each colour

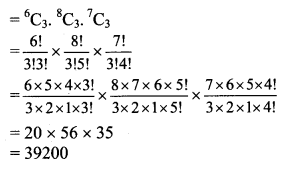
Question 8.
Find the number of ways of selecting a team of 3 boys and 2 girls from 6 boys and 4 girls.
Solution:
There are 6 boys and 4 girls.
A team of 3 boys and 2 girls is to be selected.
∴ 3 boys can be selected from 6 boys in ⁶C₃ ways.
2 girls can be selected from 4 girls in ⁴C₂ ways.
∴ Number of ways the team can be selected

Question 9.
After a meeting, every participant shakes hands with every other participants. If the number of handshakes is 66, find the number of participants in the meeting.
Solution:
Let there be n participants present in the meeting.
A handshake occurs between 2 persons.
∴ Number of handshakes = ⁿC₂
Given 66 handshakes were exchanged.
66 = ⁿC₂

Question 11.
Find the number of diagonals of an n-sided polygon. In particular, find the number of diagonals when
(i) n = 10
(ii) n = 15
(iii) n = 12
(iv) n = 8
Solution:
In n-sided polygon, there are ‘n’ points and ‘n’ sides.
∴ Through ‘n’ points we can draw ⁿC₂ lines including sides.
∴ Number of diagonals in n sided polygon = ⁿC₂ – n (n = number of sides)

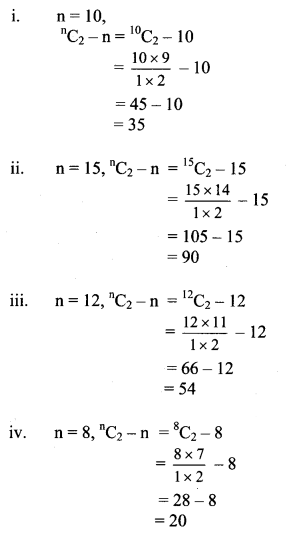
Question 12.
There are 20 straight lines in a plane so that no two lines are parallel and no three lines are concurrent. Determine the number of points of intersection.
Solution:
There are 20 lines such that no two of them are parallel and no three of them are concurrent.
Since no two lines are parallel, they intersect at a point.
∴ Number of points of intersection if no two lines are parallel and no three lines are concurrent

Question 16.
Find n if,
(i) ⁿC₈ = ⁿC₁₂
Solution:
ⁿC₈ = ⁿC₁₂
If ⁿC_x = ⁿC_y, then either x = y or x = n – y
∴ 8 = 12 or 8 = n – 12
But 8 = 12 is not possible
∴ 8 = n – 12
∴ n = 20

(ii) ²³C_3n = ²³C_2n+3
Solution:
²³C_3n = ²³C_2n+3
If ⁿC_x = ⁿC_y, then either x = y or x = n – y
∴ 3n = 2n + 3 or 3n = 23 – 2n – 3
∴ n = 3 or n = 4

∴ ⁿC_r = ⁿC_n-r
∴ ²¹C₁₂ = ²¹C₉
∴ n = 2 is a right answer.

(iv) ²ⁿC_r-1 = ²ⁿC_r+1
Solution:
²ⁿC_r-1 = ²ⁿC_r+1
If ⁿC_x = ⁿC_y, then either x = y or x = n – y
∴ r – 1 = r + 1 or r – 1 = 2n – (r + 1)
But r – 1 = r + 1 is not possible
∴ r – 1 = 2n – (r + 1)
∴ r + r = 2n
∴ r = n

Check:
²ⁿC_r-1 = ²ⁿC_n-1
and ²ⁿC_r+1 = ²ⁿC_n+1
using ⁿC_r = ⁿC_n-r, we have
²ⁿC_n+1 = ²ⁿC_2n-(n+1) = ²ⁿC_n-1
∴ ²ⁿC_r-1 = ²ⁿC_r+1

(v) ⁿC_n-2 = 15
Solution:
ⁿC_n-2 = 15
∴ ⁿC₂ = 15 …..[∵ ⁿC_r = ⁿC_n-r]

= 6435 – 462
= 5973

Question 21.
In how many ways can a boy invite his 5 friends to a party so that at least three join the party?
Solution:
Boy can invite = (3 or 4 or 5 friends)
Consider the following table:

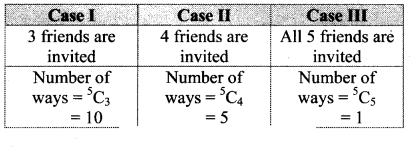
∴ Number of ways a boy can invite his friends to a party so that three or more of join the party = 10 + 5 + 1 = 16

Question 22.
A group consists of 9 men and 6 women. A team of 6 is to be selected. How many of possible selections will have at least 3 women?
Solution:
There are 9 men and 6 women.
A team of 6 persons is to be formed such that it consist of at least 3 women.
Consider the following table:

∴ No. of ways this can be done = 1680 + 540 + 54 + 1 = 2275
∴ 2275 teams can be formed if team consists of at least 3 women.

Question 23.
A committee of 10 persons is to be formed from a group of 10 women and 8 men. How many possible committees will have at least 5 women? How many possible committees will have men in majority?
Solution:
(i) A committee of 10 persons is to be formed from 10 women and 8 men such that the committee contains at least 5 women.
Consider the following table:

∴ Number of committees with at least 5 women
= 14112 + 14700 + 6720 + 1260 + 81
= 36873

(ii) Number of committees with men in majority = Total number of committees – (Number of committees with women in majority + women and men equal in number)
= ¹⁸C₁₀ – 36873
= ¹⁸C₈ – 36873
= 43758 – 36873
= 6885

Question 24.
A question paper has two sections. Section I has 5 questions and section II has 6 questions. A student must answer at least two questions from each section among 6 questions he answers. How many different choices does the student have in choosing questions?
Solution:
There are 11 questions, out of which 5 questions are from section I and 6 questions are from section II.
The student has to select 6 questions taking at least 2 questions from each section.
Consider the following table:

∴ Number of choices = 150 + 200 + 75 = 425
∴ In 425 ways students can select 6 questions, taking at least 2 questions from each section.

Question 25.
There are 3 wicketkeepers and 5 bowlers among 22 cricket players. A team of 11 player is to be selected so that there is exactly one wicketkeeper and at least 4 bowlers in the team. How many different teams can be formed?
Solution:
There are 22 cricket players, of which 3 are wicketkeepers and 5 are bowlers.
A team of 11 players is to be chosen such that exactly one wicket keeper and at least 4 bowlers are to be included in the team.
Consider the following table:

∴ Number of ways a team of 11 players can be selected
= 45045 + 6006
= 51051

Question 26.
Five students are selected from 11. How many ways can these students be selected if
(a) two specified students are selected?
(b) two specified students are not selected?
Solution:
5 students are to be selected from 11 students.
(a) When 2 specified students are included,
then remaining 3 students can be selected from (11 – 2) = 9 students.
∴ Number of ways of selecting 3 students from 9 students = ⁹C₃

Download PDF

Maharashtra Board Solutions Class 11-Arts & Science Maths (Part 2): Chapter 3- Permutations and Combination

Download PDF: Maharashtra Board Solutions Class 11-Arts & Science Maths (Part 2): Chapter 3- Permutations and Combination PDF

Chapterwise Maharashtra Board Solutions Class 11 Arts & Science Maths (Part 2) :

• Chapter 1- Complex Numbers
• Chapter 2- Sequences and Series
• Chapter 3- Permutations and Combination
• Chapter 4- Methods of Induction and Binomial Theorem
• Chapter 5- Sets and Relations
• Chapter 6- Functions
• Chapter 7- Limits
• Chapter 8- Continuity
• Chapter 9- Differentiation

FAQs

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC. 

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.

Read More

• NCERT Solutions for 3rd Class Environmental Studies: Chapter 17-Here Comes a Letter
• RD Sharma Solutions for Class 11 Maths Chapter 16–Permutations
• NCERT Solutions for 8th Class Maths: Chapter 6-Squares and Square Roots
• ISC 11th Result 2020- Board Exam
• NCERT Solutions for 8th Class Maths: Chapter 7-Cubes and Cube Roots

IndCareer Board Book Solutions App

IndCareer Board Book App provides complete study materials for students from classes 1 to 12 of Board. The App contains complete solutions of NCERT books, notes, and other important materials for students. Download the IndCareer Board Book Solutions now.