Selina Class 10 ICSE Solutions Mathematics : Chapter 4 - Linear Inequations (in one variable)

Class 10: Maths Chapter 4 solutions. Complete Class 10 Maths Chapter 4 Notes.

Selina Class 10 ICSE Solutions Mathematics : Chapter 4 - Linear Inequations (in one variable)

Selina 10th Maths Chapter 4, Class 10 Maths Chapter 4 solutions

Exercise 4A

Question 1.

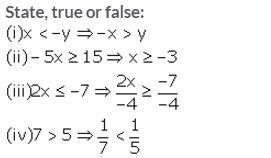
Solution:

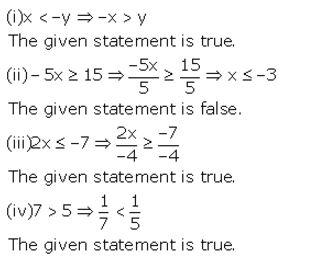
Question 2.
State, whether the following statements are true or false:
(i) a < b, then a – c < b – c (ii) If a > b, then a + c > b + c
(iii) If a < b, then ac > bc
(iv) If a > b, then ac<bc
(v) If a – c > b – d, then a + d > b + c
(vi) If a < b, and c > 0, then a – c > b – c
Where a, b, c and d are real numbers and c ≠ 0.
Solution:
(i) a < b ⇒ a – c < b – c The given statement is true.
(ii) If a > b ⇒ a + c > b + c
The given statement is true.
(iii) If a < b ⇒ ac < bc The given statement is false.
(iv) If a > b ⇒ ac>bc
The given statement is false.
(v) If a – c > b – d ⇒ a + d > b + c
The given statement is true.
(vi) If a < b ⇒ a – c < b – c (Since, c > 0)
The given statement is false.

Question 3.
If x ∈ N, find the solution set of inequations.
(i) 5x + 3 ≤ 2x + 18
(ii) 3x – 2 < 19 – 4x
Solution:
(i) 5x + 3 ≤ 2x + 18
5x – 2x ≤ 18 – 3
3x ≤ 15
x ≤ 5
Since, x ∈ N, therefore solution set is {1, 2, 3, 4, 5}.
(ii) 3x – 2 < 19 – 4x
3x + 4x < 19 + 2
7x < 21
x < 3
Since, x ∈ N, therefore solution set is {1, 2}.

Question 4.

Solution:
(i) x + 7 ≤ 11
x ≤ 11 – 7
x ≤ 4
Since, the replacement set = W (set of whole numbers)
⇒ Solution set = {0, 1, 2, 3, 4}
(ii) 3x – 1 > 8
3x > 8 + 1
x > 3
Since, the replacement set = W (set of whole numbers)
⇒ Solution set = {4, 5, 6, …}
(iii) 8 – x > 5
– x > 5 – 8
– x > -3
x < 3
Since, the replacement set = W (set of whole numbers)
⇒ Solution set = {0, 1, 2}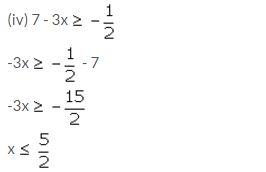

Since, the replacement set = W (set of whole numbers)
∴ Solution set = {0, 1, 2}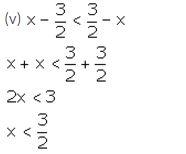

Since, the replacement set = W (set of whole numbers)
∴ Solution set = {0, 1}
(vi) 18 ≤ 3x – 2
18 + 2 ≤ 3x
20 ≤ 3x
x ≥ 203
Since, the replacement set = W (set of whole numbers)
∴ Solution set = {7, 8, 9, …}

Question 5.
Solve the inequation:
3 – 2x ≥ x – 12 given that x ∈ N.
Solution:
3 – 2x ≥ x – 12
-2x – x ≥ -12 – 3
-3x ≥ -15
x ≤ 5
Since, x ∈ N, therefore,
Solution set = {1, 2, 3, 4, 5}

Question 6.
If 25 – 4x ≤ 16, find:
(i) the smallest value of x, when x is a real number,
(ii) the smallest value of x, when x is an integer.
Solution:
25 – 4x ≤ 16
-4x ≤ 16 – 25
-4x ≤ -9
x ≥ 94
x ≥ 2.25
(i) The smallest value of x, when x is a real number, is 2.25.
(ii) The smallest value of x, when x is an integer, is 3.

Question 7.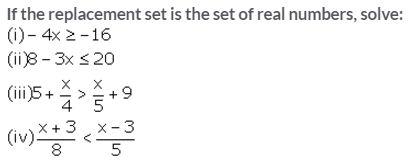

Solution:

Question 8.

Solution: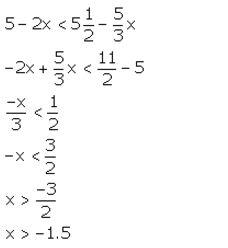

Thus, the required smallest value of x is -1.

Question 9.
Find the largest value of x for which
2(x – 1) ≤ 9 – x and x ∈ W.
Solution:
2(x – 1) ≤ 9 – x
2x – 2 ≤ 9 – x
2x + x ≤ 9 + 2
3x ≤ 11
x ≤ 113
x ≤ 3.67
Since, x ∈ W, thus the required largest value of x is 3.

Question 10.

Solution:

Question 11.
Given x ∈ {integers}, find the solution set of:
-5 ≤ 2x – 3 < x + 2
Solution: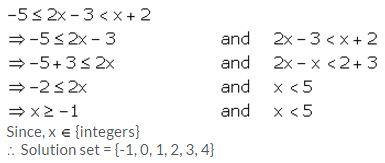

Question 12.
Given x ∈ {whole numbers}, find the solution set of:
-1 ≤ 3 + 4x < 23

Solution:

Exercise 4B

Question 1.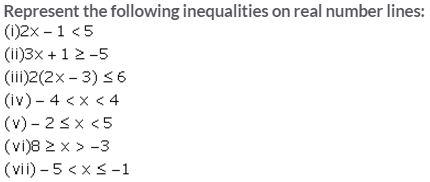

Solution: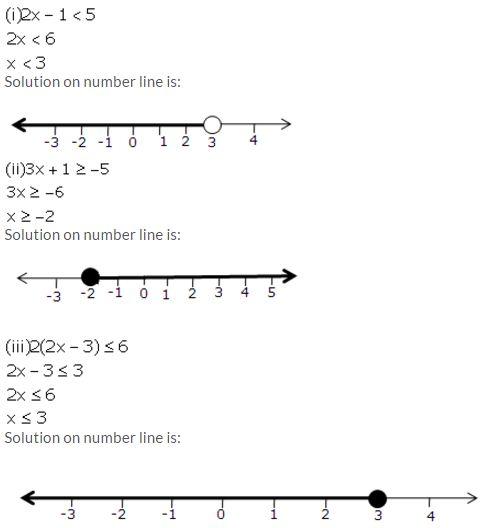

Question 2.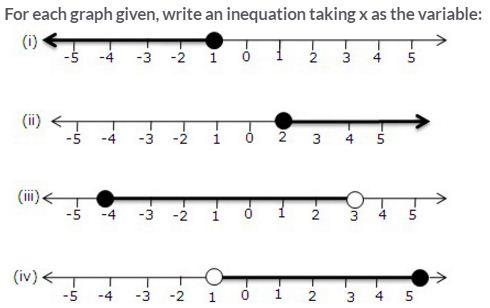

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.
x ∈ {real numbers} and -1 < 3 – 2x ≤ 7, evaluate x and represent it on a number line.
Solution:
-1 < 3 – 2x ≤ 7
-1 < 3 – 2x and 3 – 2x ≤ 7
2x < 4 and -2x ≤ 4
x < 2 and x ≥ -2
Solution set = {-2 ≤ x < 2, x ∈ R}
Thus, the solution can be represented on a number line as:

Question 6.
List the elements of the solution set of the inequation
-3 < x – 2 ≤ 9 – 2x; x ∈ N.
Solution:
-3 < x – 2 ≤ 9 – 2x
-3 < x – 2 and x – 2 ≤ 9 – 2x
-1 < x and 3x ≤ 11
-1 < x ≤ 113
Since, x ∈ N
∴ Solution set = {1, 2, 3}

Question 7.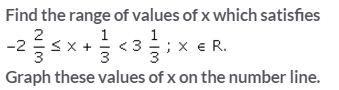

Solution:

Question 8.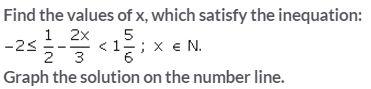

Solution: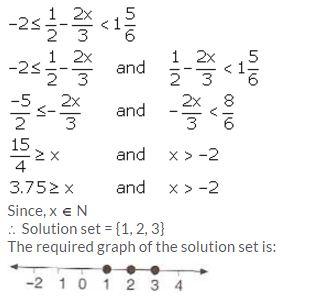

Question 9.
Given x ∈ {real numbers}, find the range of values of x for which -5 ≤ 2x – 3 < x + 2 and represent it on a number line.
Solution:
-5 ≤ 2x – 3 < x + 2
-5 ≤ 2x – 3 and 2x – 3 < x + 2
-2 ≤ 2x and x < 5
-1 ≤ x and x < 5
Required range is -1 ≤ x < 5.
The required graph is:

Question 10.
If 5x – 3 ≤ 5 + 3x ≤ 4x + 2, express it as a ≤ x ≤ b and then state the values of a and b.
Solution:
5x – 3 ≤ 5 + 3x ≤ 4x + 2
5x – 3 ≤ 5 + 3x and 5 + 3x ≤ 4x + 2
2x ≤ 8 and -x ≤ -3
x ≤ 4 and x ≥ 3
Thus, 3 ≤  x ≤ 4.
Hence, a = 3 and b = 4.

Question 11.
Solve the following inequation and graph the solution set on the number line:
2x – 3 < x + 2 ≤ 3x + 5, x ∈ R.
Solution:
2x – 3 < x + 2 ≤ 3x + 5
2x – 3 < x + 2 and x + 2 ≤ 3x + 5
x < 5 and -3 ≤ 2x
x < 5 and -1.5 ≤ x
Solution set = {-1.5 ≤ x < 5}
The solution set can be graphed on the number line as:

Question 12.
Solve and graph the solution set of:
(i) 2x – 9 < 7 and 3x + 9 ≤ 25, x ∈ R (ii) 2x – 9 ≤ 7 and 3x + 9 > 25, x ∈ I
(iii) x + 5 ≥ 4(x – 1) and 3 – 2x < -7, x ∈ R
Solution:

Question 13.
Solve and graph the solution set of:
(i) 3x – 2 > 19 or 3 – 2x ≥ -7, x ∈ R
(ii) 5 > p – 1 > 2 or 7 ≤ 2p – 1 ≤ 17, p ∈ R
Solution:
(i) 3x – 2 > 19 or 3 – 2x ≥ -7
3x > 21 or -2x ≥ -10
x > 7 or x ≤ 5
Graph of solution set of x > 7 or x ≤ 5 = Graph of points which belong to x > 7 or x ≤ 5 or both.
Thus, the graph of the solution set is:

(ii) 5 > p – 1 > 2 or 7 ≤ 2p – 1 ≤ 17
6 > p > 3 or 8 ≤ 2p ≤ 18
6 > p > 3 or 4 ≤ p ≤ 9
Graph of solution set of 6 > p > 3 or 4 ≤ p ≤ 9
= Graph of points which belong to 6 > p > 3 or 4 ≤ p ≤ 9 or both
= Graph of points which belong to 3 < p ≤ 9
Thus, the graph of the solution set is:

Question 14.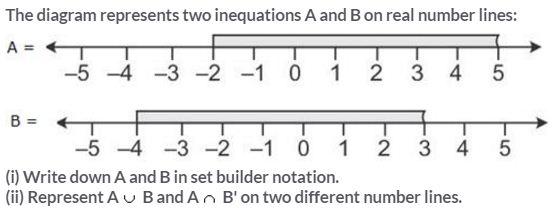

Solution:
(i) A = {x ∈ R: -2 ≤ x < 5}
B = {x ∈ R: -4 ≤ x < 3}
(ii) A ∩ B = {x ∈ R: -2 ≤ x < 5}
It can be represented on number line as:

B’ = {x ∈ R: 3 < x ≤ -4}
A ∩ B’ = {x ∈ R: 3 ≤ x < 5}
It can be represented on number line as: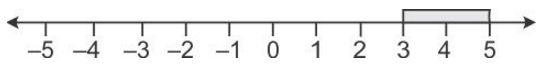

Question 15.
Use real number line to find the range of values of x for which:
(i) x > 3 and 0 < x < 6
(ii) x < 0 and -3 ≤ x < 1
(iii) -1 < x ≤ 6 and -2 ≤ x ≤ 3
Solution:
(i) x > 3 and 0 < x < 6
Both the given inequations are true in the range where their graphs on the real number lines overlap.
The graphs of the given inequations can be drawn as:

From both graphs, it is clear that their common range is
3 < x < 6
(ii) x < 0 and -3 ≤ x < 1
Both the given inequations are true in the range where their graphs on the real number lines overlap.
The graphs of the given inequations can be drawn as:

From both graphs, it is clear that their common range is
-3 ≤ x < 0
(iii) -1 < x ≤ 6 and -2 ≤ x ≤ 3
Both the given inequations are true in the range where their graphs on the real number lines overlap.
The graphs of the given inequations can be drawn as: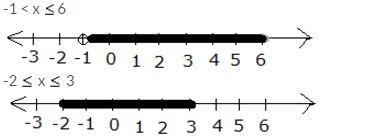

From both graphs, it is clear that their common range is
-1 < x ≤ 3

Question 16.
Illustrate the set {x: -3 ≤ x < 0 or x > 2, x ∈ R} on the real number line.
Solution:
Graph of solution set of -3 ≤ x < 0 or x > 2
= Graph of points which belong to -3 ≤ x < 0 or x > 2 or both
Thus, the required graph is:

Question 17.
Given A = {x: -1 < x ≤ 5, x ∈ R} and B = {x: -4 ≤ x < 3, x ∈ R}
Represent on different number lines:
(i) A ∩ B
(ii) A’ ∩ B
(iii) A – B
Solution:

Question 18.
P is the solution set of 7x – 2 > 4x + 1 and Q is the solution set of 9x – 45 ≥ 5(x – 5); where x ∈ R. Represent:
(i) P ∩ Q
(ii) P – Q
(iii) P ∩ Q’
on different number lines.
Solution:

Question 19.

Solution:

Question 20.
Given: A = {x: -8 < 5x + 2 ≤ 17, x ∈ I}, B = {x: -2 ≤ 7 + 3x < 17, x ∈ R}
Where R = {real numbers} and I = {integers}. Represent A and B on two different number lines. Write down the elements of A ∩ B.
Solution: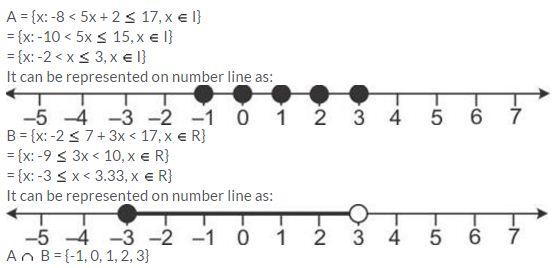

Question 21.
Solve the following inequation and represent the solution set on the number line 2x – 5 ≤ 5x +4 < 11, where x ∈ I
Solution:

Question 22.

Solution: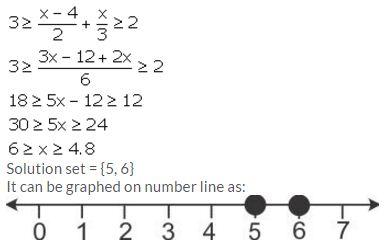

Question 23.
Given:
A = {x: 11x – 5 > 7x + 3, x ∈ R} and
B = {x: 18x – 9 ≥ 15 + 12x, x ∈ R}.
Find the range of set A ∩ B and represent it on number line.
Solution:
A = {x: 11x – 5 > 7x + 3, x ∈ R}
= {x: 4x > 8, x ∈ R}
= {x: x > 2, x ∈ R}
B = {x: 18x – 9 ≥ 15 + 12x, x ∈ R}
= {x: 6x ≥ 24, x ∈ R}
= {x: x ≥ 4, x ∈ R}
A ∩ B = {x: x ≥ 4, x ∈ R}
It can be represented on number line as:

Question 24.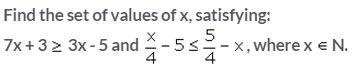

Solution: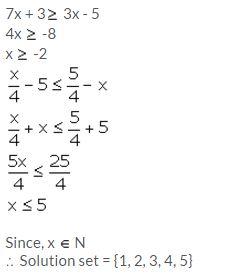

Question 25.

Solution: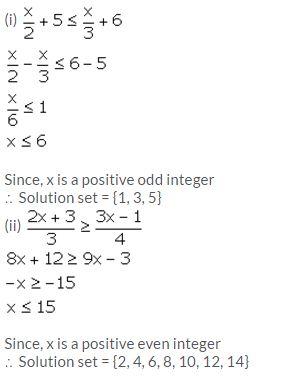

Question 26.

Solution:

Question 27.
Find three consecutive largest positive integers such that the sum of one-third of first, one-fourth of second and one-fifth of third is atmost 20.
Solution:
Let the required integers be x, x + 1 and x + 2.
According to the given statement,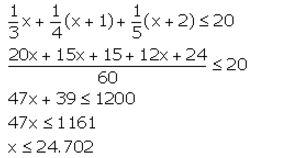

Thus, the largest value of the positive integer x is 24.
Hence, the required integers are 24, 25 and 26.

Question 28.
Solve the given inequation and graph the solution on the number line.
2y – 3 < y + 1 ≤ 4y + 7, y ∈ R
Solution:
2y – 3 < y + 1 ≤ 4y + 7, y ∈ R
⇒ 2y – 3 – y < y + 1 – y ≤ 4y + 7 – y
⇒ y – 3 < 1 ≤ 3y + 7
⇒ y – 3 < 1 and 1 ≤ 3y + 7
⇒ y < 4 and 3y ≥ 6 ⇒ y ≥ – 2
⇒ – 2 ≤ y < 4
The graph of the given equation can be represented on a number line as:

Question 29.
Solve the inequation:
3z – 5 ≤ z + 3 < 5z – 9, z ∈ R.
Graph the solution set on the number line.
Solution:
3z – 5 ≤ z + 3 < 5z – 9
3z – 5 ≤ z + 3 and z + 3 < 5z – 9
2z ≤ 8 and 12 < 4z
z ≤ 4 and 3 < z
Since, z R
∴ Solution set = {3 < z ≤ 4, x ∈ R }
It can be represented on a number line as:

Question 30.

Solution: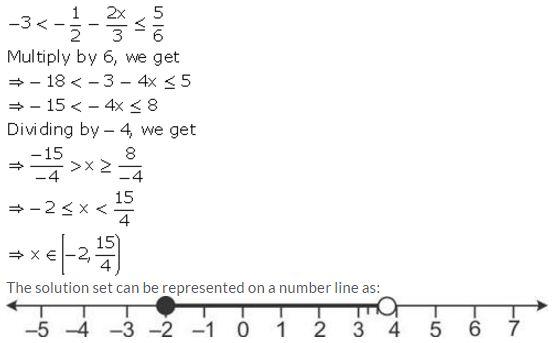

Question 31.

Solution:

Question 32.

Solution: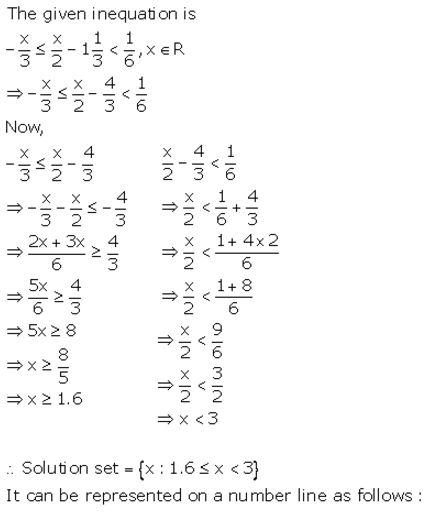

Question 33.

Solution:

Question 34.
Solve the following in equation and write the solution set:
13x – 5 < 15x + 4 < 7x + 12, x ∈ R
Solution: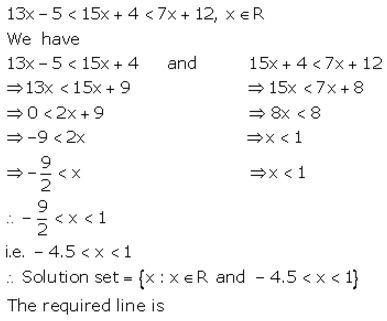

Question 35.
Solve the following inequation, write the solution set and represent it on the number line.
-3(x – 7) ≥ 15 – 7x > x+1/3, x R.
Solution:

Question 36.
Solve the following inequation and represent the solution set on a number line.

Solution:

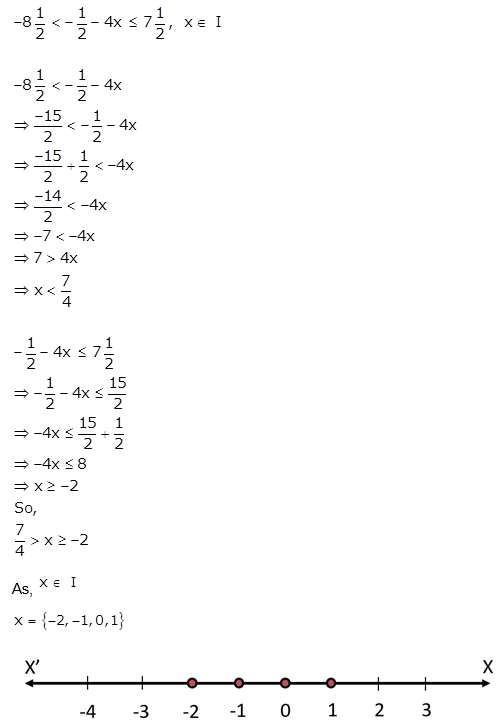
Download PDF

Selina Class 10 ICSE Solutions Mathematics : Chapter 1 - GST (Goods and Services Tax)

Download PDF: Selina Class 10 ICSE Solutions Mathematics : Chapter 1 - GST (Goods and Services Tax) PDF

Chapterwise Selina Publishers ICSE Solutions for Class 10 Maths :

• Chapter 1 - GST (Goods and Services Tax)
• Chapter 2 - Banking (Recurring Deposit Accounts)
• Chapter 3 -Shares and Dividends
• Chapter 4 - Linear Inequations (in one variable)
• Chapter 5 - Quadratic Equations
• Chapter 6 - Solving Simple Problems (Based on Quadratic Equations)
• Chapter 7 - Ratio and Proportion (Including Properties and Uses)
• Chapter 8 - Remainder and Factor Theorems
• Chapter 9 - Matrices
• Chapter 10- Arithmetic Progression
• Chapter 11- Geometric Progression
• Chapter 12- Reflection
• Chapter 13 - Section and Mid-Point Formula
• Chapter 14- Equation of a Line
• Chapter 15- Similarity
• Chapter 16- Loci (Locus and Its Constructions)
• Chapter 17- Circles
• Chapter 18- Tangents and Intersecting Chords
• Chapter 19- Constructions (Circles)
• Chapter 20- Cylinder, Cone and Sphere
• Chapter 21- Trigonometrical Identities
• Chapter 22- Heights and Distances
• Chapter 23- Graphical Representation
• Chapter 24- Measures of Central Tendency
• Chapter 25- Probability

About Selina Publishers ICSE

Selina Publishers has been serving the students since 1976 and is one of the quality ICSE school textbooks publication houses. Mathematics and Science books for classes 6-10 form the core of our business, apart from certain English and Hindi literature as well as a few primary books. All these books are based upon the syllabus published by the Council for the I.C.S.E. Examinations, New Delhi. The textbooks are composed by a panel of subject experts and vetted by teachers practising in ICSE schools all over the country. Continuous efforts are made in complying with the standards and ensuring lucidity and clarity in content, which makes them stand tall in the industry.