Selina Class 10 ICSE Solutions Mathematics : Chapter 17- Circles

Class 10: Maths Chapter 17 solutions. Complete Class 10 Maths Chapter 17 Notes.

Selina Class 10 ICSE Solutions Mathematics : Chapter 17- Circles

Selina 10th Maths Chapter 17, Class 10 Maths Chapter 17 solutions

Exercise 17A

Question 1.
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. Find ∠AOC. Show your steps of working.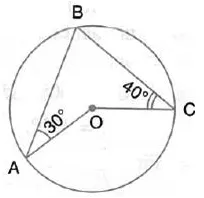

Solution:

Question 2.
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
(i) Prove that AC is a diameter of the circle.
(ii) Find ∠ACB.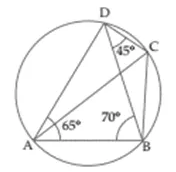

Solution:

Question 3.
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
(i) ∠ OCA,
(ii) ∠OAC.

Solution: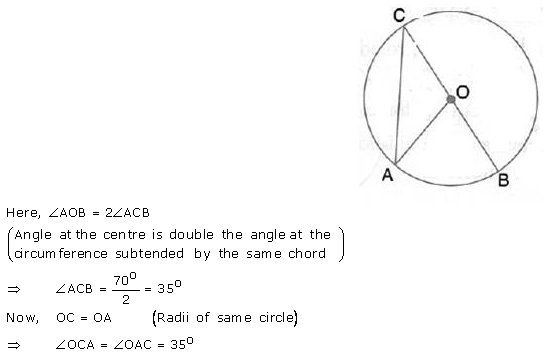

Question 4.
In each of the following figures, O is the centre of the circle. Find the values of a, b, and c.

Solution:

Question 5.
In each of the following figures, O is the centre of the circle. Find the value of a, b, c and d.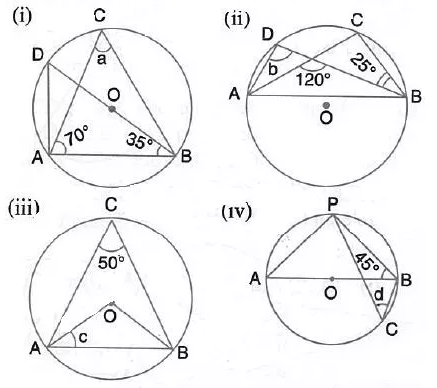

Solution: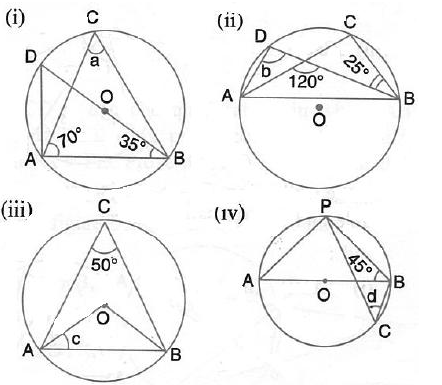

Question 6.
In the figure, AB is common chord of the two circles. If AC and AD are diameters; prove that D, B and C are in a straight line. O₁ and O₂ are the centres of two circles.

Solution: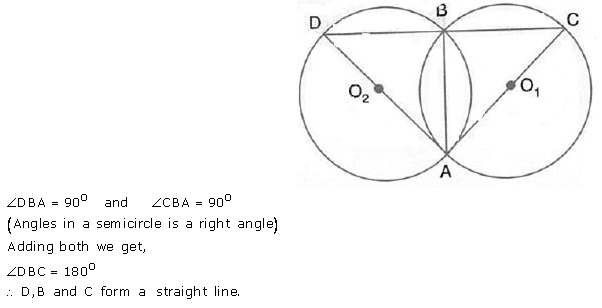

Question 7.
In the figure given beow, find :
(i) ∠ BCD,
(ii) ∠ ADC,
(iii) ∠ ABC.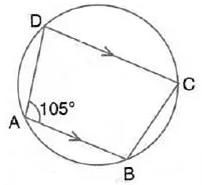

Show steps of your workng.
Solution: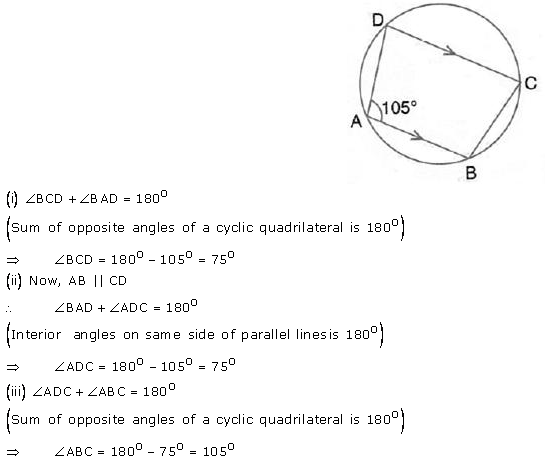

Question 8.
In the given figure, O is centre of the circle. If ∠ AOB = 140° and ∠ OAC = 50°; find :
(i) ∠ ACB,
(ii) ∠ OBC,
(iii) ∠ OAB,
(iv) ∠CBA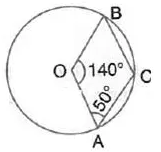

Solution:

Question 9.
Calculate :
(i) ∠ CDB,
(ii) ∠ ABC,
(iii) ∠ ACB.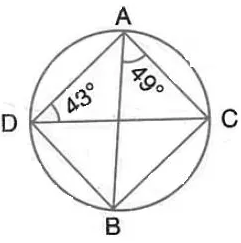

Solution:

Question 10.
In the figure given below, ABCD is a eyclic quadrilateral in which ∠ BAD = 75°; ∠ ABD = 58° and ∠ADC = 77°. Find:
(i) ∠ BDC,
(ii) ∠ BCD,
(iii) ∠ BCA.

Solution: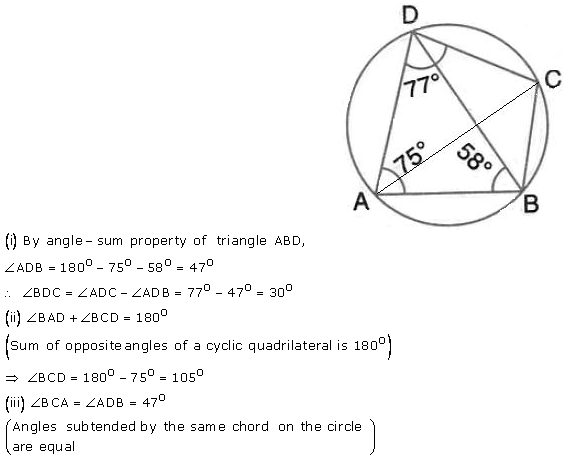

Question 11.
In the following figure, O is centre of the circle and ∆ ABC is equilateral. Find :
(i) ∠ ADB
(ii) ∠ AEB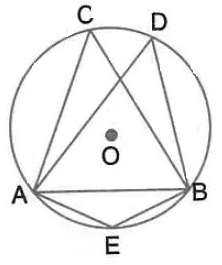

Solution:

Question 12.
Given—∠ CAB = 75° and ∠ CBA = 50°. Find the value of ∠ DAB + ∠ ABD

Solution:

Question 13.
ABCD is a cyclic quadrilateral in a circle with centre O.
If ∠ ADC = 130°; find ∠ BAC.

Solution: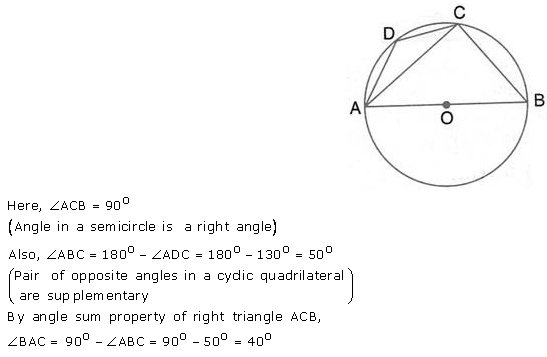

Question 14.
In the figure given below, AOB is a diameter of the circle and ∠ AOC = 110°. Find ∠ BDC.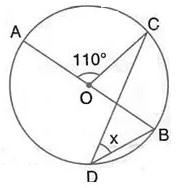

Solution: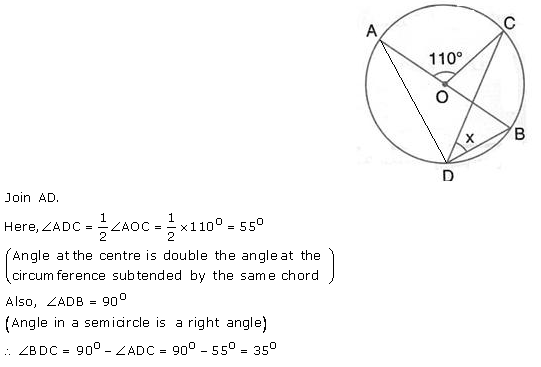

Question 15.
In the following figure, O is centre of the circle,
∠ AOB = 60° and ∠ BDC = 100°.
Find ∠ OBC.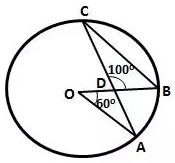

Solution:

Question 16.
ABCD is a cyclic quadrilateral in which ∠ DAC = 27°; ∠ DBA = 50° and ∠ ADB = 33°.
Calculate :
(i) ∠ DBC,
(ii) ∠ DCB,
(iii) ∠ CAB.

Solution:

Question 17.
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°. Find the number of degrees in:
(i) ∠DCE;
(ii) ∠ABC.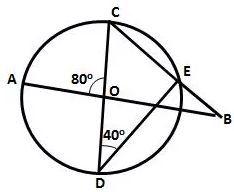

Solution:

Question 17 (old).
In the figure given below, AB is diameter of the circle whose centre is O. Given that:
∠ ECD = ∠ EDC = 32°.

Show that ∠ COF = ∠ CEF.
Solution:

Question 18.
In the figure given below, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that AB = BE.

Solution: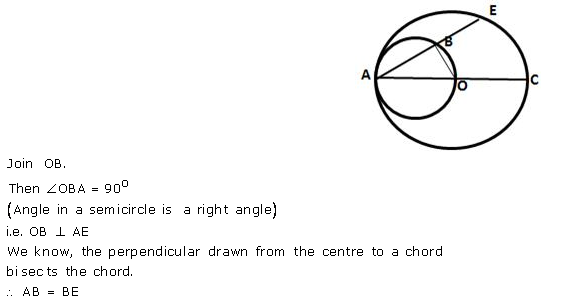

Question 19.
In the following figure,
(i) if ∠BAD = 96°, find BCD and
(ii) Prove that AD is parallel to FE.

Solution: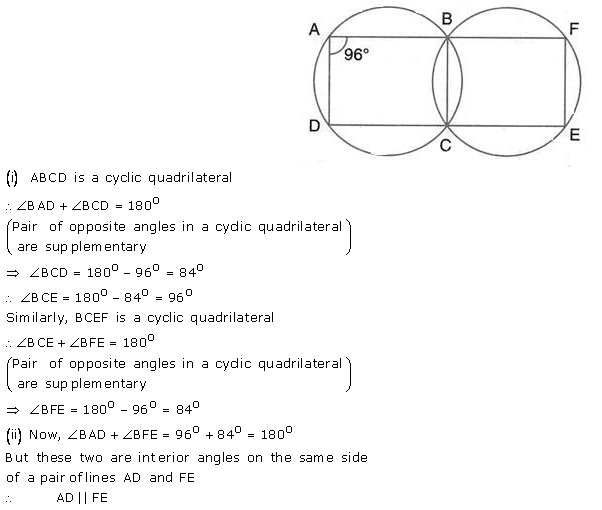

Question 20.
Prove that:
(i) the parallelogram, inscribed in a circle, is a rectangle.
(ii) the rhombus, inscribed in a circle, is a square.
Solution:

Question 21.
In the following figure, AB = AC. Prove that DECB is an isosceles trapezium.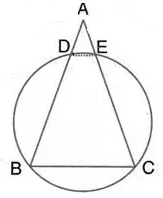

Solution:

Question 22.
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
Solution:

Question 23.
The figure given below, shows a circle with centre O. Given: ∠ AOC = a and ∠ ABC = b.
(i) Find the relationship between a and b
(ii) Find the measure of angle OAB, if OABC is a parallelogram.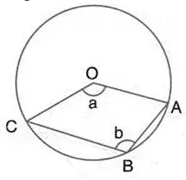

Solution: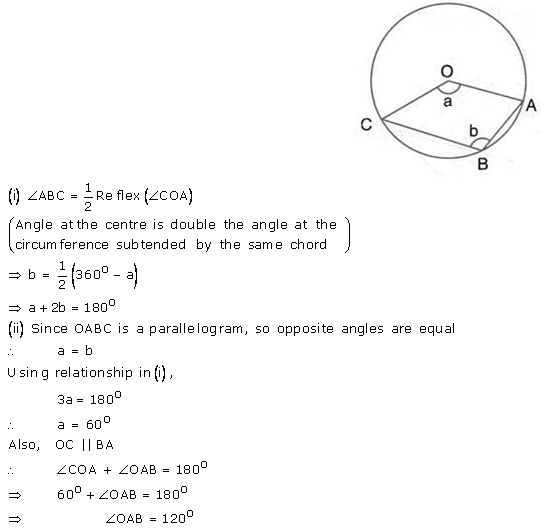

Question 24.
Two chords AB and CD intersect at P inside the circle. Prove that the sum of the angles subtended by the arcs AC and BD as the centre O is equal to twice the angle APC.
Solution:

Question 24 (old).
ABCD is a quadrilateral inscribed in a circle having ∠A = 60°; O is the centre of the circle. Show that: ∠OBD + ∠ODB = ∠CBD + ∠CDB
Solution:

Question 25.
In the figure given RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°
Calculate:
(i) ∠RNM;
(ii) ∠NRM.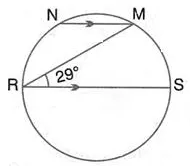

Solution: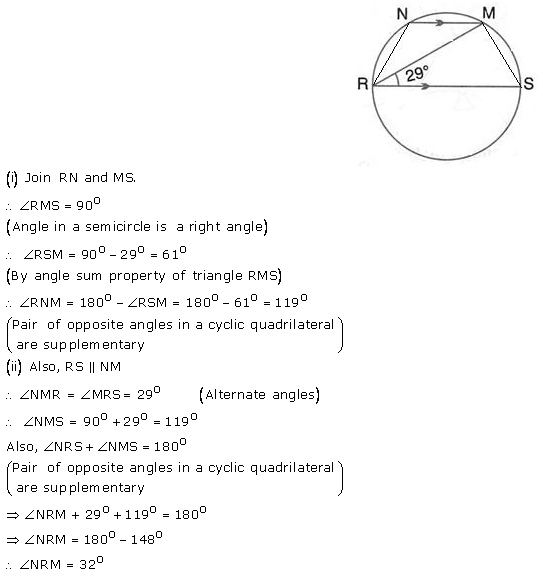

Question 26.
In the figure given alongside, AB || CD and O is the centre of the circle. If ∠ ADC = 25°; find the angle AEB. Give reasons in support of your answer.

Solution:

Question 27.
Two circles intersect at P and Q. Through P, a straight line APB is drawn to meet the circles in A and B. Through Q, a straight line is drawn to meet the circles at Cand D. Prove that AC is parallel to BD.

Solution: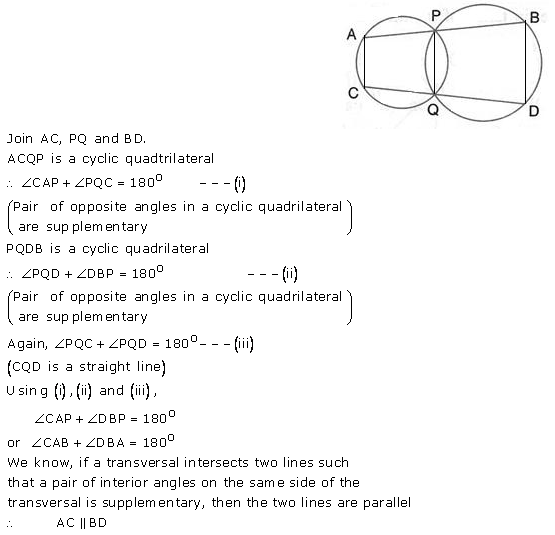

Question 28.
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.
Solution:

Question 29.
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find:
(i) ∠PRB
(ii) ∠PBR
(iii) ∠BPR.

Solution:

Question 30.
In the given figure, SP is the bisector of angle RPT and PQRS is a cyclic quadrilateral. Prove that: SQ = SR.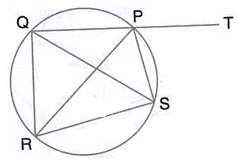

Solution: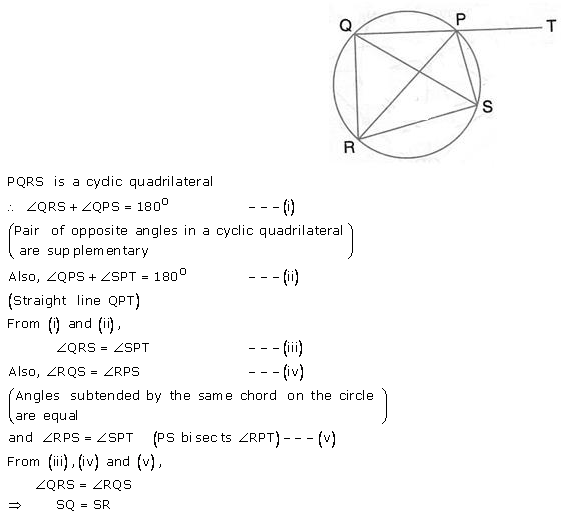

Question 31.
In the figure, O is the centre of the circle, ∠AOE = 150°, DAO = 51°. Calculate the sizes of the angles CEB and OCE.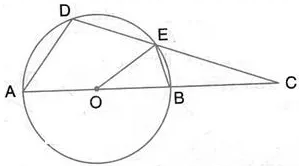

Solution: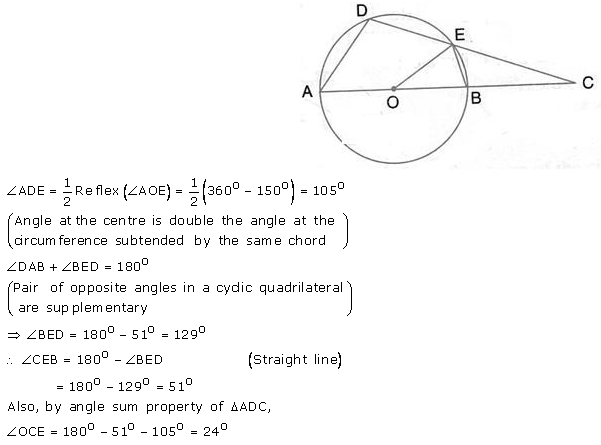

Question 32.
In the figure, P and Q are the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x.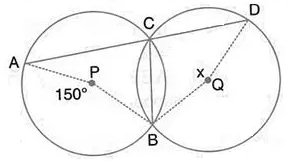

Solution:

Question 33.
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°. Calculate, in terms of a°, the value of:
(i) obtuse ∠AOB
(ii) ∠ACB
(iii) ∠ADB.
Give reasons for your answers clearly.

Solution:

Question 34.
In the given figure, O is the centre of the circle and ∠ ABC = 55°. Calculate the values of x and y.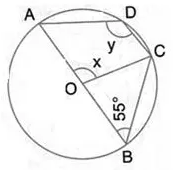

Solution: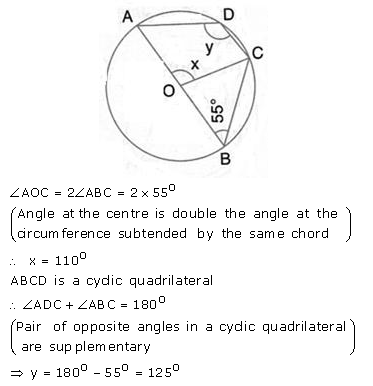

Question 35.
In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that ∠BCD = 2∠ABE

Solution: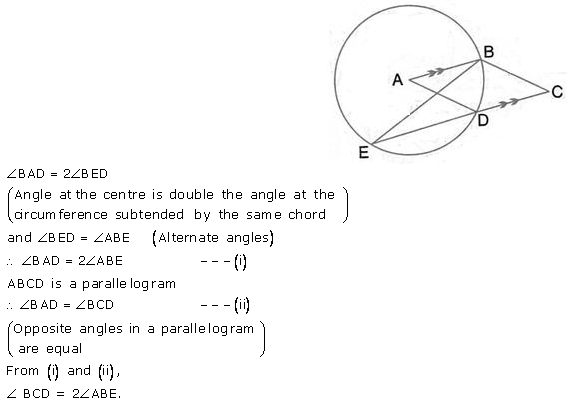

Question 36.
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate:
(i) ∠ DAB,
(ii) ∠BDC.

Solution:

Question 37.
∠ In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠ EAB = 63°; calculate:
(i) ∠EBA,
(ii) BCD.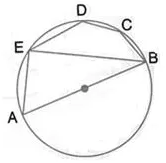

Solution:

Question 38.
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°; calculate:
(i) ∠ DAB,
(ii) ∠ DBA,
(iii) ∠ DBC,
(iv) ∠ ADC.
Also, show that the ∆AOD is an equilateral triangle.

Solution: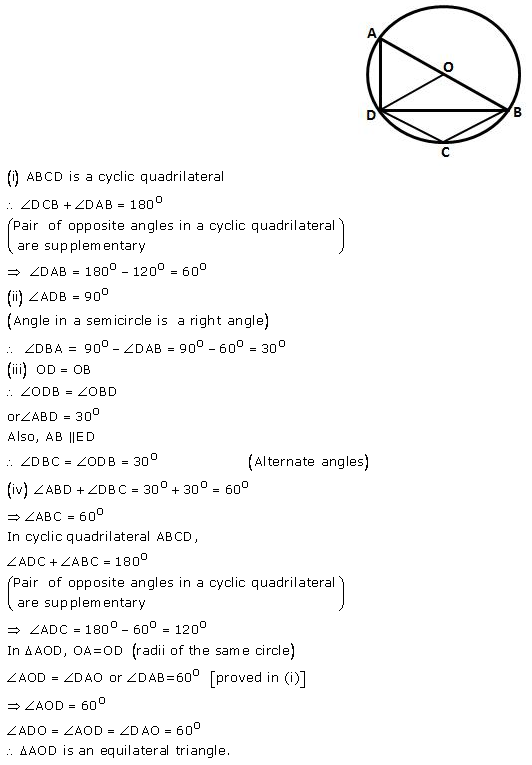

Question 39.
In the given figure, I is the incentre of the ∆ ABC. Bl when produced meets the circumcirle of ∆ ABC at D. Given ∠BAC = 55° and ∠ ACB = 65°, calculate:
(i) ∠DCA,
(ii) ∠ DAC,
(iii) ∠DCI,
(iv) ∠AIC.

Solution:

Question 40.
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that:
(i) ∠ABC = 2 ∠APQ
(ii) ∠ACB = 2 ∠APR
(iii) ∠QPR = 90° – 12BAC

Solution:

Question 40 (old).
The sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E; the sides DA and CB are produced to meet at F. If ∠BEC = 42° and ∠BAD = 98°; calculate:
(i) ∠AFB,
(ii) ∠ADC.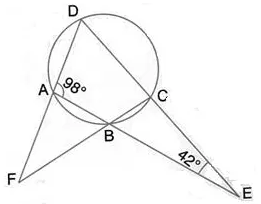

Solution: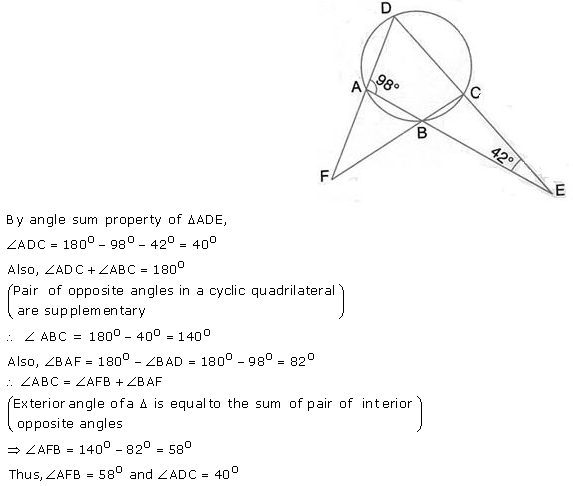

Question 41.
Calculate the angles x, y and z if: x3=y4=z5

Solution: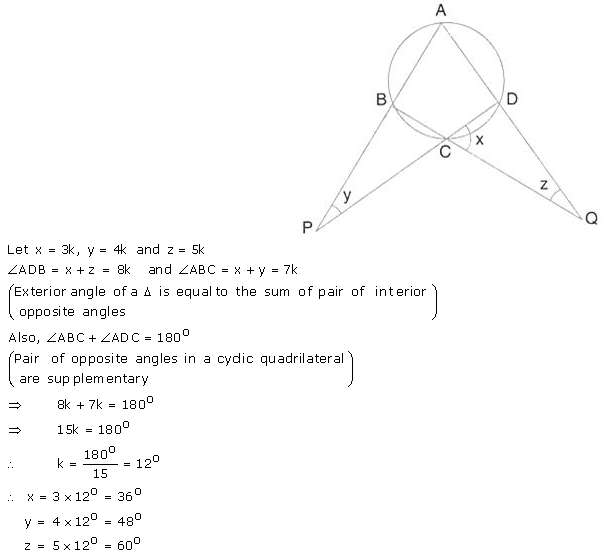

Question 42.
In the given figure, AB = AC = CD and ∠ADC = 38°. Calculate:
(i) Angle ABC
(ii) Angle BEC.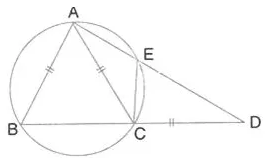

Solution:

Question 43.
In the given figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, and r in terms of x.

Solution:

Question 44.
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80° and angle ACE = 10°. Calculate:
(i) Angle BEC;
(ii) Angle BCD;
(iii) Angle CED.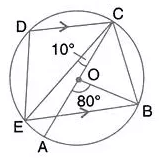

Solution:

Question 45.
In the given figure, AE is the diameter of circle. Write down the numerical value of ∠ABC + ∠CDE. Give reasons for your answer.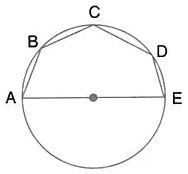

Solution: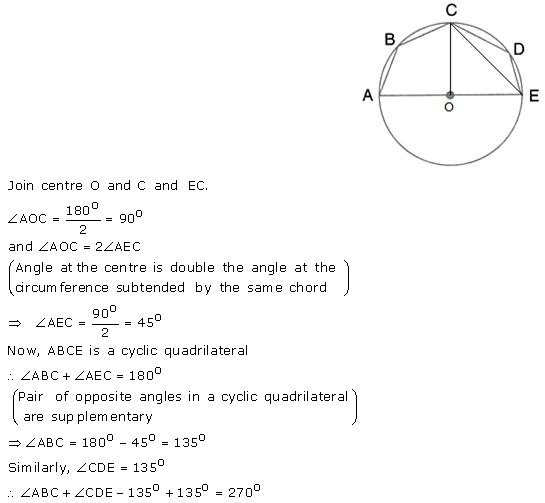

Question 46.
In the given figure, AOC is a diameter and AC is parallel to ED. If ∠CBE = 64°, calculate ∠DEC.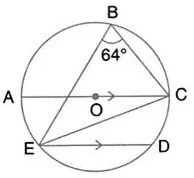

Solution:

Question 47.
Use the given figure to find
(i) ∠BAD
(ii) ∠DQB.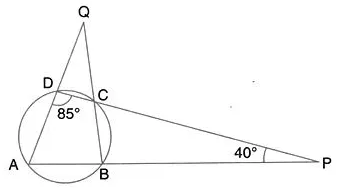

Solution:

Question 48.
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = x°; find (in terms of x) the values of:
(i) ∠COB
(ii) ∠DOC
(iii) ∠DAC
(iv) ∠ADC.

Solution: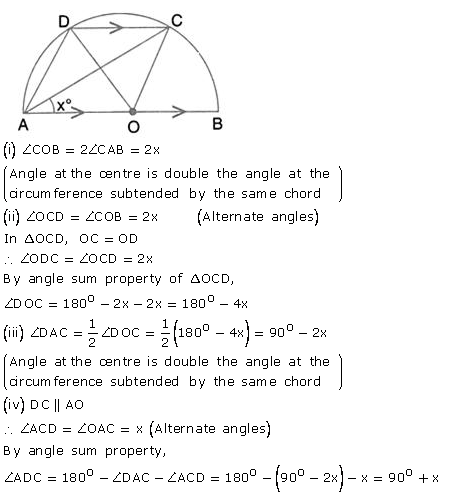

Question 49.
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA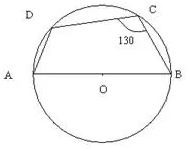

Solution:

Question 50.
In the given figure, PQ is the diameter of the circle whose centre is O. Given ∠ROS = 42°; calculate ∠RTS.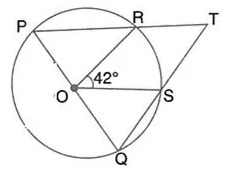

Solution:

Question 51.
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°; calculate
(i) ∠RPQ
(ii) ∠STP.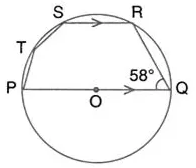

Solution: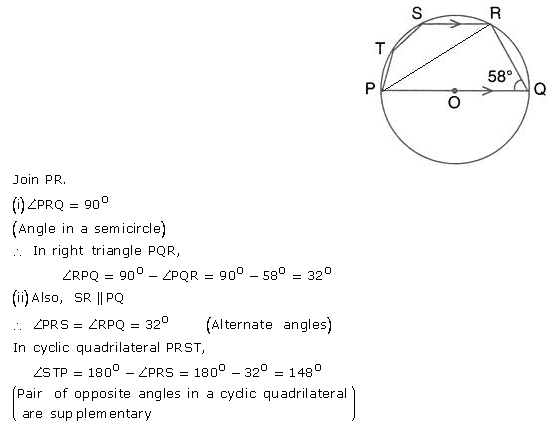

Question 52.
AOD = 60°; calculate the numerical values of:
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠AOD = 60°; calculate the numerical values of:
(i) ∠ABD,
(ii) ∠DBC,
(iii) ∠ADC.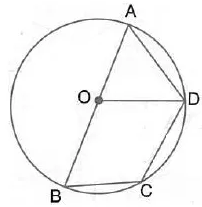

Solution:

Question 53.
In the given figure, the centre of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40″; find:
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABD,
(iv) ∠ADB.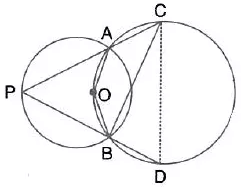

Solution:

Question 54.
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°; find:
(i) ∠BCD,
(ii) ∠ACB.
Hence, show that AC is a diameter.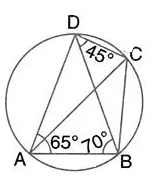

Solution:

Question 55.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
Solution:

Question 56.
The given figure shows a circle with centre O and ∠ABP = 42°. Calculate the measure of
(i) ∠PQB
(ii) ∠QPB + ∠PBQ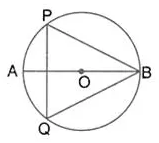

Solution: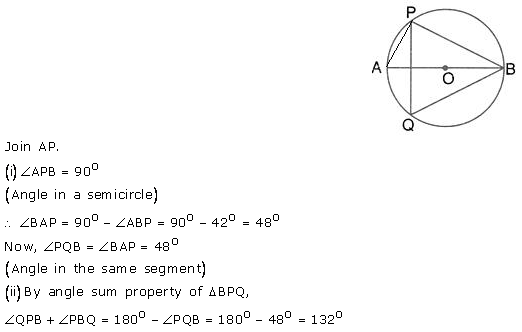

Question 57.
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. If ∠ MAD =x and ∠BAC = y.
(i) express ∠AMD in terms of x.
(ii) express ∠ABD in terms of y.
(iii) prove that : x = y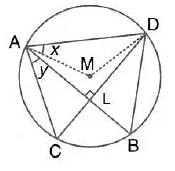

Solution:

Question 61 (old).
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
Solution:

Exercise 17B

Question 1.
In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal.
Prove it.
Solution:

Question 2.
In the following figure, AD is the diameter of the circle with centre 0. chords AB, BC and CD are equal. If ∠DEF = 110°, calculate:
(i) ∠ AFE,
(ii) ∠FAB.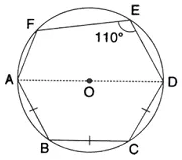

Solution:

Question 3.
If two sides of a cycli-quadrilateral are parallel; prove thet:
(i) its other two side are equal.
(ii) its diagonals are equal.
Solution: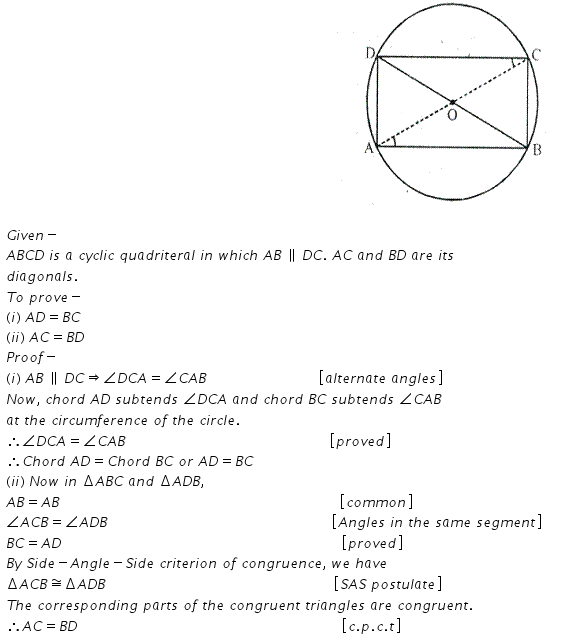

Question 4.
The given figure show a circle with centre O. also, PQ = QR = RS and ∠PTS = 75°. Calculate:
(i) ∠POS,
(ii) ∠ QOR,
(iii) ∠PQR.

Solution: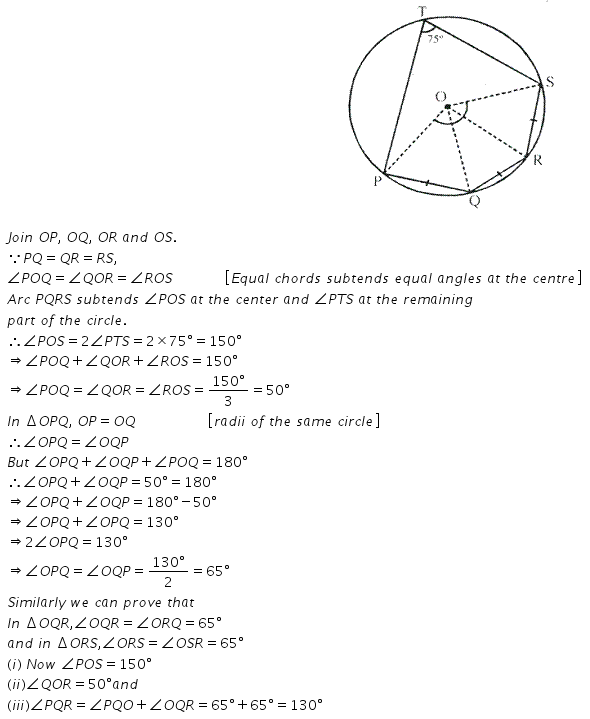

Question 5.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. calculate the sizes of:
(i) ∠ AOB,
(ii) ∠ ACB,
(iii) ∠ABC.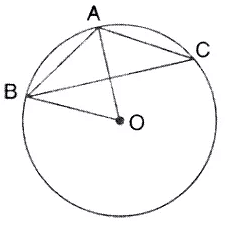

Solution:

Question 6.
In a regular pentagon ABCDE, inscribed in a circle; find ratio between angle EDA and angel ADC.
Solution:

Question 7.
In the given figure. AB = BC = CD and ∠ABC = 132°, calculate:
(i) ∠AEB,
(ii) ∠ AED,
(iii) ∠COD.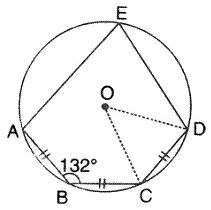

Solution:

Question 8.
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find:
(i) ∠ CAB,
(ii) ∠ADB.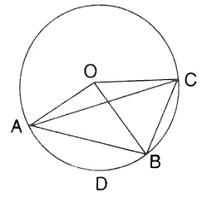

Solution:

Question 9.
The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon. Find the angles of triangle ABC.

Solution:

Question 10.
In the given figire, BD is a side of a regularhexagon, DC is a side of a regular pentagon and AD is adiameter. Calculate:
(i) ∠ ADC
(ii) ∠BAD,
(iii) ∠ABC
(iv) ∠ AEC.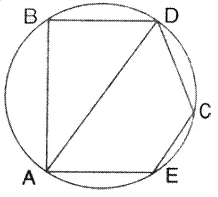

Solution:

Exercise 17C

Question 1.
In the given circle with diametre AB, find the value of x.

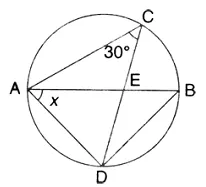
Solution: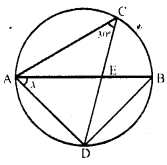

∠ABD = ∠ACD = 30° (Angle in the same segment)
Now in ∆ ADB,
∠BAD + ∠ADB + ∠DBA = 180° (Angles of a A)
But ∠ADB = 90° (Angle in a semi-circle)
∴ x + 90° + 30° = 180° ⇒ x + 120° = 180°
∴ x= 180° – 120° = 60° Ans.

Question 1.
In the given figure, O is the centre of the circle with radius 5 cm, OP and OQ are perpendiculars to AB and CD respectively. AB = 8cm and CD = 6cm. Determine the length of PQ.

Solution:

Question 2.
In the given figure, ABC is a triangle in which ∠ BAC = 30° Show that BC is equal to the radius of the circum-circle of the triangle ABC, whose centre is O.

Solution: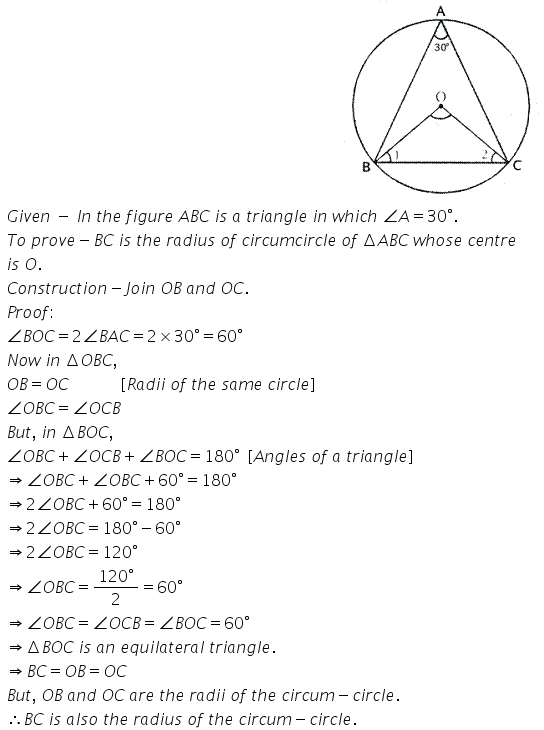

Question 3.
Prove that the circle drawn on any one a the equalside of an isoscele triangle as diameter bisects the base.
Solution: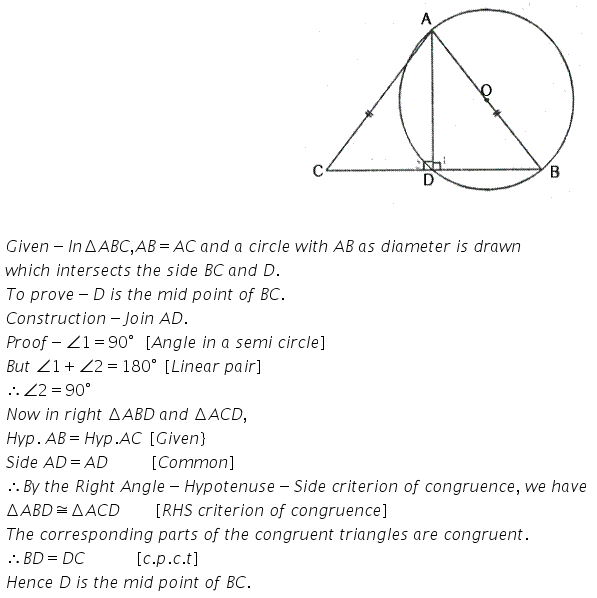

Question 3 (old).
The given figure show two circles with centres A and B; and radii 5 cm and 3cm respectively, touching each other internally. If the perpendicular bisector of AB meets the bigger circle in P and Q, find the length of PQ.

Solution:

Question 4.
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠ CBE = 65°, calculate ∠DEC.

Solution: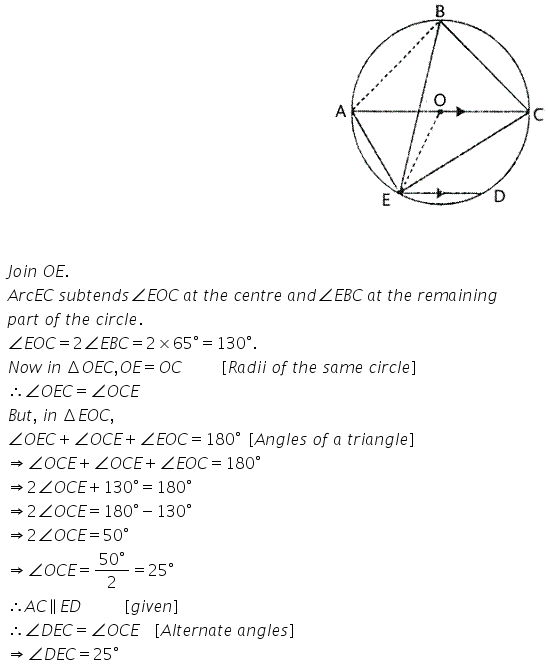

Question 5.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
Solution:

Question 6.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate:
(i) ∠BDC
(ii) ∠BEC
(iii) ∠BAC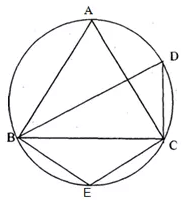

Solution:

Question 7.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Provet that the points B, C, E and D are concyclic.
Solution:

Question 7 (old).
Chords AB and CD of a circle intersect each other at point P such that AP = CP.
Show that: AB = CD.

Solution: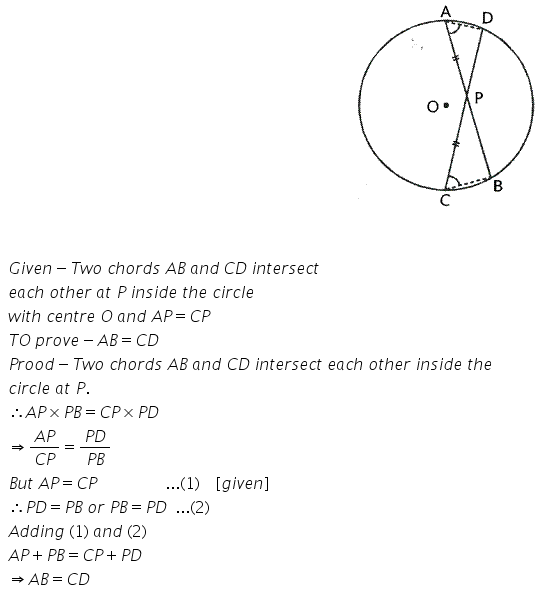

Question 8.
In the given rigure, ABCD is a cyclic eqadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ ADC = 92°, ∠ FAE = 20°; determine ∠ BCD. Given reason in support of your answer.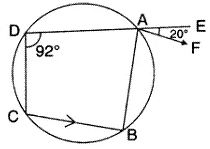

Solution:

Question 9.
If I is the incentre of triangle ABC and Al when produced meets the cicrumcircle of triangle ABC in points D. if ∠ BAC = 66° and ∠ = 80o.calculate:
(i) ∠ DBC
(ii) ∠ IBC
(iii) ∠ BIC.

Solution:

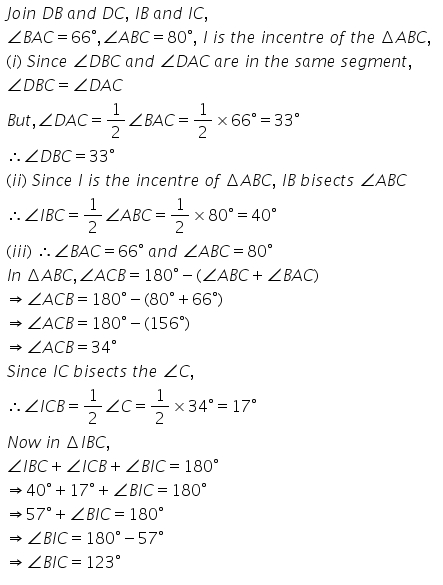
Question 10.
In the given figure, AB = AD = DC = PB and ∠ DBC = x°. Determine, in terms of x:
(i) ∠ ABD,
(ii) ∠ APB.
Hence or otherwise, prove thet AP is parallel to DB.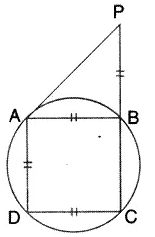

Solution:

Question 11.
In the given figure; ABC, AEQ and CEP are straight lines. Show that ∠APE and ∠ CQE are supplementary.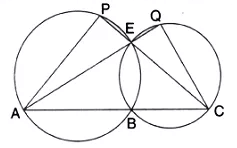

Solution: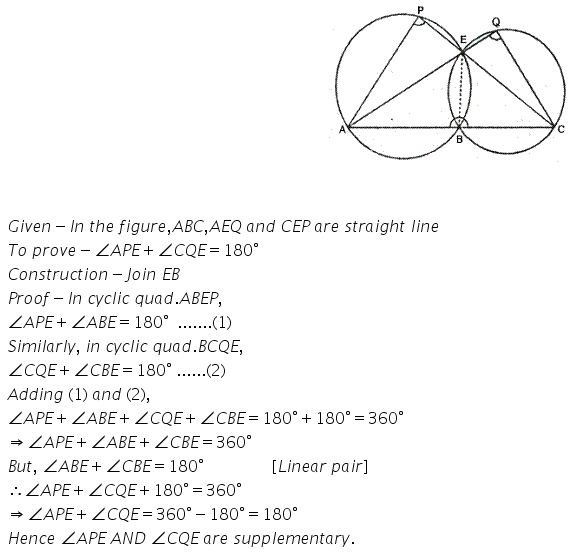

Question 12.
In the given, AB is the diameter of the circle with centre O.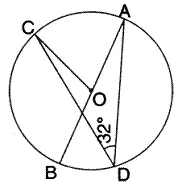

If ∠ ADC = 32°, find angle BOC.
Solution: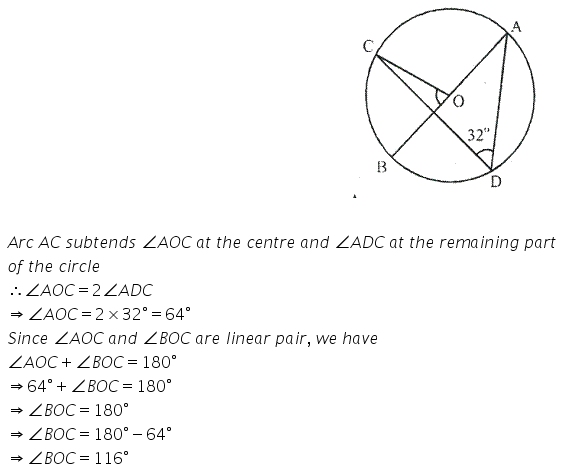

Question 13.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ prouduced meet at point A: whereas sides PQ and SR produced meet at point B.
If ∠A: ∠B = 2 : 1;find angles A and B.
Solution: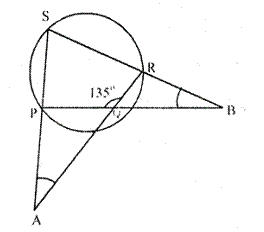

Question 17 (old).
If the following figure, AB is the diameter of a circle with centre O and CD is the chord with lengh equal radius OA.
If AC produced and BD produed meet at point p; show that ∠APB = 60°

Solution:

Question 14.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.

If the bisector of angle A meet BC at point E and the given circle at point F, prove that:
(i) EF = FC
(ii) BF =DF
Solution: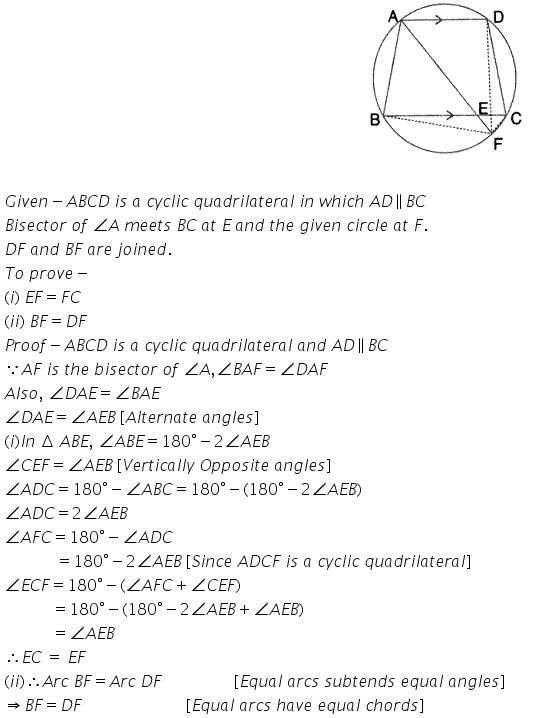

Question 15.
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point e; whereas sides BC and AD produced meet at point F. I f ∠ DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
Solution:

Question 16.
The following figure shows a cicrcle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, Find the perimetre of the cyclic quadrilateral PORS.

Solution:

Question 17.
In the following figure, AB is the diameter of a circle with centre O. If chord AC = chord AD.prove that:
(i) arc BC = arc DB
(ii) AB is bisector of ∠ CAD.
Further if the lenghof arc AC is twice the lengthof arc BC find :
(a) ∠ BAC
(b) ∠ ABC

Solution: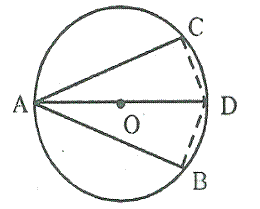

Question 18.
In cyclic quadrilateral ABCD; AD = BC, ∠ = 30° and ∠ = 70°; find;
(i) ∠ BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ ADC
Solution: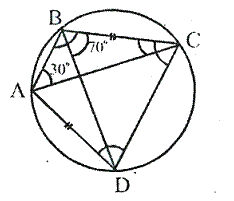

Question 19.
In the given figure, ∠ACE = 43° and ∠ = 62°; find the values of a, b and c.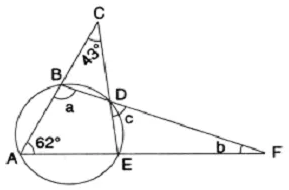

Solution: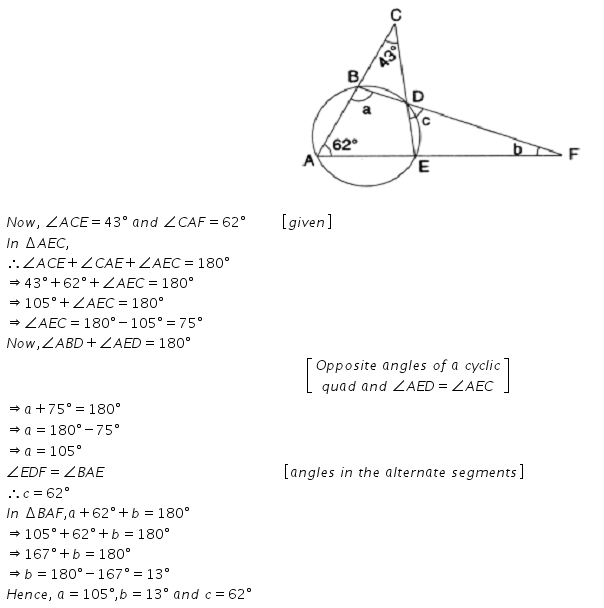

Question 20.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠ BAC = 25°
Find
(i) ∠ CAD
(ii) ∠ CBD
(iii) ∠ ADC

Solution: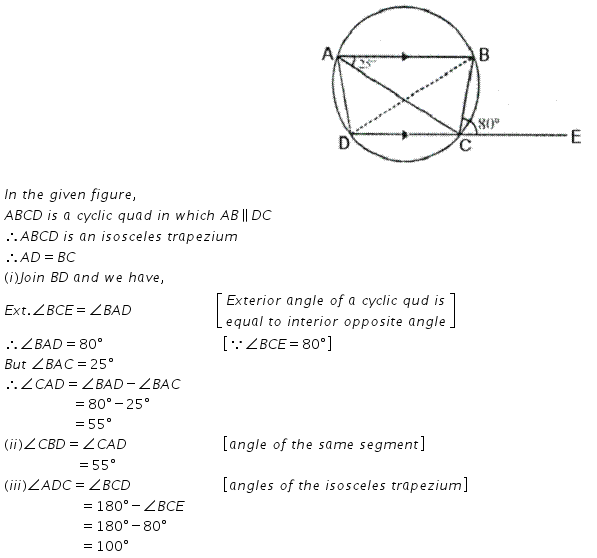

Question 21.
ABCD is a cyclic quadrilateral of a circle with centre o such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle..if AD and BC produced meet at P, show that APB =60°
Solution: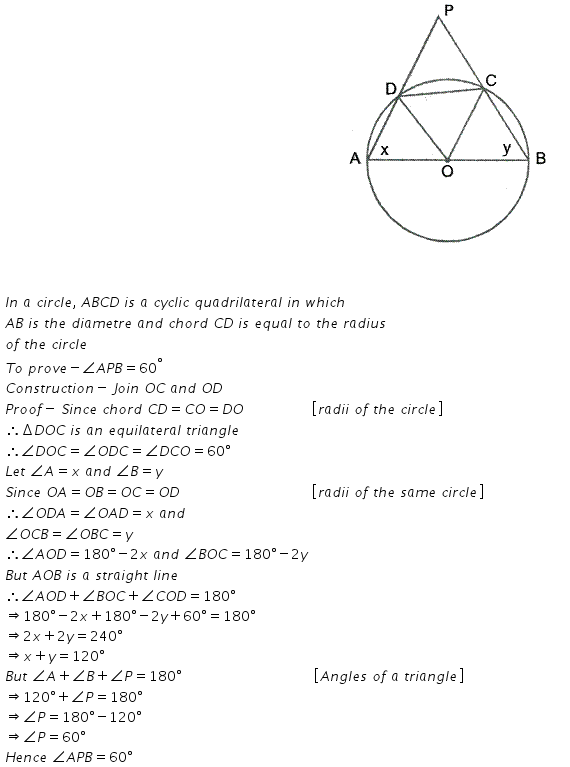

Question 22.
In the figure, given alongside, CP bisects angle ACB. Show that DP bisects angle ADB.

Solution:

Question 23.
In the figure, given below, AD = BC, ∠ BAC = 30° and ∠ = 70° find:
(i) ∠ BCD
(ii) ∠ BCA
(iii) ∠ ABC
(iv) ∠ADC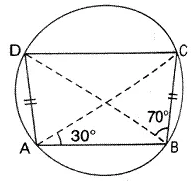

Solution:

Question 24.
In the figure given below, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED (2016)
Solution:
i. AD is parallel to BC, i.e., OD is parallel to BC and BD is transversal.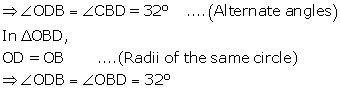

Question 25.
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
i. ∠BCD
ii. ∠BOD
iii. ∠OBD

Solution:
∠DAE and ∠DAB are linear pair
So,
∠DAE + ∠DAB = 180°
∴∠DAB = 110°

Also,
∠BCD + ∠DAB = 180°……Opp. Angles of cyclic quadrilateral BADC
∴∠BCD = 70°
∠BCD = 12 ∠BOD…angles subtended by an arc on the centre and on the circle
∴∠BOD = 140°

In ΔBOD,
OB = OD……radii of same circle
So,
∠OBD =∠ODB……isosceles triangle theorem
∠OBD + ∠ODB + ∠BOD = 180°……sum of angles of triangle
2∠OBD = 40°
∠OBD = 20°

Download PDF

Selina Class 10 ICSE Solutions Mathematics : Chapter 17- Circles

Download PDF: Selina Class 10 ICSE Solutions Mathematics : Chapter 17- Circles PDF

Chapterwise Selina Publishers ICSE Solutions for Class 10 Maths :

• Chapter 1 – GST (Goods and Services Tax)
• Chapter 2 – Banking (Recurring Deposit Accounts)
• Chapter 3 -Shares and Dividends
• Chapter 4 – Linear Inequations (in one variable)
• Chapter 5 – Quadratic Equations
• Chapter 6 – Solving Simple Problems (Based on Quadratic Equations)
• Chapter 7 – Ratio and Proportion (Including Properties and Uses)
• Chapter 8 – Remainder and Factor Theorems
• Chapter 9 – Matrices
• Chapter 10- Arithmetic Progression
• Chapter 11- Geometric Progression
• Chapter 12- Reflection
• Chapter 13 – Section and Mid-Point Formula
• Chapter 14- Equation of a Line
• Chapter 15- Similarity
• Chapter 16- Loci (Locus and Its Constructions)
• Chapter 17- Circles
• Chapter 18- Tangents and Intersecting Chords
• Chapter 19- Constructions (Circles)
• Chapter 20- Cylinder, Cone and Sphere
• Chapter 21- Trigonometrical Identities
• Chapter 22- Heights and Distances
• Chapter 23- Graphical Representation
• Chapter 24- Measures of Central Tendency
• Chapter 25- Probability

About Selina Publishers ICSE

Selina Publishers has been serving the students since 1976 and is one of the quality ICSE school textbooks publication houses. Mathematics and Science books for classes 6-10 form the core of our business, apart from certain English and Hindi literature as well as a few primary books. All these books are based upon the syllabus published by the Council for the I.C.S.E. Examinations, New Delhi. The textbooks are composed by a panel of subject experts and vetted by teachers practising in ICSE schools all over the country. Continuous efforts are made in complying with the standards and ensuring lucidity and clarity in content, which makes them stand tall in the industry.