Selina Class 10 ICSE Solutions Mathematics : Chapter 11- Geometric Progression

Class 10: Maths Chapter 11 solutions. Complete Class 10 Maths Chapter 11 Notes.

Selina Class 10 ICSE Solutions Mathematics : Chapter 11- Geometric Progression

Selina 10th Maths Chapter 11, Class 10 Maths Chapter 11 solutions

Exercise 11A

Question 1.
Find, which of the following sequence form a G.P. :
(i) 8, 24, 72, 216, ……
(ii) 18,124,172,1216, ……..
(iii) 9, 12, 16, 24, ……
Solution 1(i).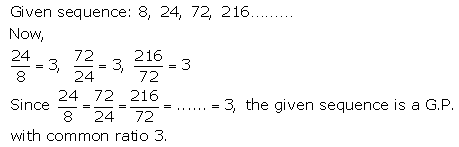

Solution 1(ii).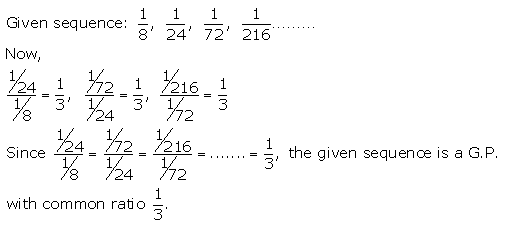

Solution 1(iii).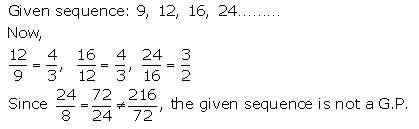

Question 2.
Find the 9th term of the series :
1, 4, 16, 64 ……..
Solution:

Question 3.
Find the seventh term of the G.P. :
1, 3–√, 3, 33–√ …..
Solution:

Question 4.
Find the 8^th term of the sequence :
34,112 3, …….
Solution:

Question 5.
Find the 10^th term of the G.P. :
Solution: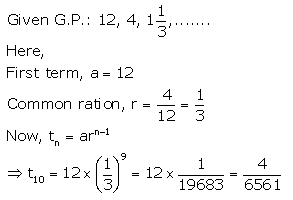

Question 6.
Find the n^th term of the series :
Solution:

Question 7.
Find the next three terms of the sequence :
5–√, 5, 55–√, ……
Solution:

Question 8.
Find the sixth term of the series :
2², 2³, 2⁴, ……….
Solution: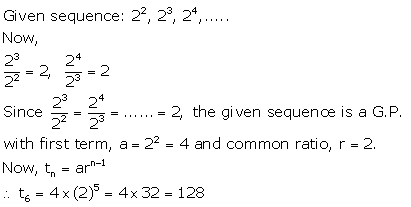

Question 9.
Find the seventh term of the G.P. :
[late]\sqrt{3}+1,1, \frac{\sqrt{3}-1}{2}[/latex], ……………..
Solution:

Question 10.
Find the G.P. whose first term is 64 and next term is 32.
Solution:

Question 11.
Find the next three terms of the series:
227,29,23, ………….
Solution:

Question 12.
Find the next two terms of the series
2 – 6 + 18 – 54 …………
Solution: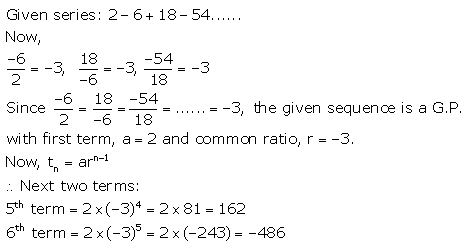

Exercise 11B

Question 1.
Which term of the G.P. :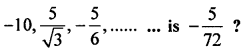

Solution:

Question 2.
The fifth term of a G.P. is 81 and its second term is 24. Find the geometric progression.
Solution:

Question 3.
Fourth and seventh terms of a G.P. are 118 and −1486 respectively. Find the GP.
Solution: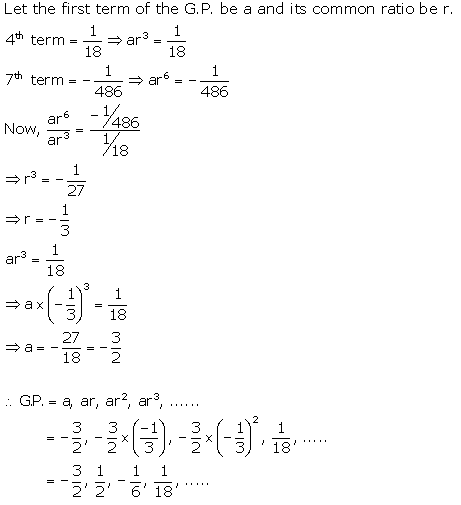

Question 4.
If the first and the third terms of a G.P. are 2 and 8 respectively, find its second term.
Solution:

Question 5.
The product of 3rd and 8th terms of a G.P. is 243. If its 4^th term is 3, find its 7^th term.
Solution:

Question 6.
Find the geometric progression with 4^th term = 54 and 7^th term = 1458.
Solution:

Question 7.
Second term of a geometric progression is 6 and its fifth term is 9 times of its third term. Find the geometric progression. Consider that each term of the G.P. is positive.
Solution:

Question 8.
The fourth term, the seventh term and the last term of a geometric progression are 10, 80 and 2560 respectively. Find its first term, common ratio and number of terms.
Solution:

Question 9.
If the 4th and 9th terms of a G.P. are 54 and 13122 respectively, find the GP. Also, find its general term.
Solution:

Question 10.
The fifth, eight and eleventh terms of a geometric progression are p, q and r respectively. Show that : q² = pr.
Solution:

Exercise 11C

Question 1.
Find the seventh term from the end of the series : 2–√ , 2, 22–√, ………. 32.
Solution: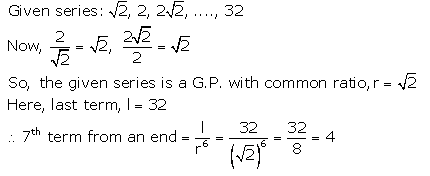

Question 2.
Find the third term from the end of the GP.
227,29,23, ………….. 162
Solution: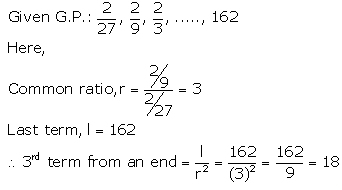

Question 3.
For the 127,19,13, ………… 81;
find the product of fourth term from the beginning and the fourth term from the end.
Solution:

Question 4.
If for a G.P., p^th, q^th and r^th terms are a, b and c respectively ; prove that :
(q – r) log a + (r – p) log b + (p – q) log c = 0
Solution:

Question 5.
If a, b and c in G.P., prove that : log aⁿ, log bⁿ and log cⁿ are in A.P.
Solution:

Question 6.
If each term of a G.P. is raised to the power x, show that the resulting sequence is also a G.P.
Solution: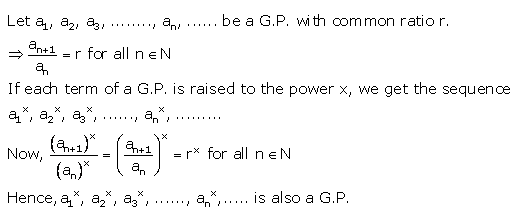

Question 7.
If a, b and c are in A.P. a, x, b are in G.P. whereas b, y and c are also in G.P. Show that : x², b², y² are in A.P.
Solution: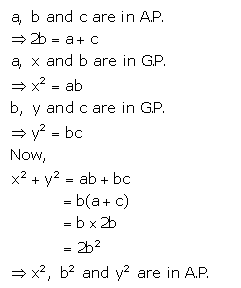

Question 8.
If a, b, c are in G.P. and a, x, b, y, c are in A.P., prove that :

Solution 8(i).

Solution 8(ii).

Question 9.
If a, b and c are in A.P. and also in G.P., show that: a = b = c.
Solution: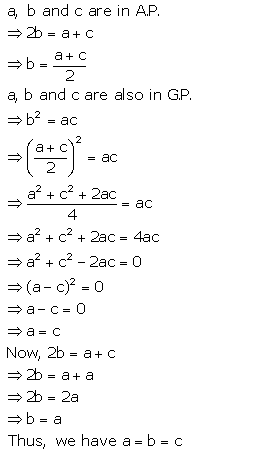

Question 10.
The first term of a G.P. is a and its n^th term is b, where n is an even number.If the product of first n numbers of this G.P. is P ; prove that : p² – (ab)ⁿ.
Solution:

Question 11.
If a, b, c and d are consecutive terms of a G.P. ; prove that :
(a² + b²), (b² + c²) and (c² + d²) are in GP.
Solution:

Question 12.
If a, b, c and d are consecutive terms of a G.P. To prove: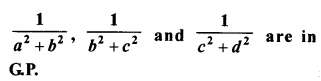

Solution: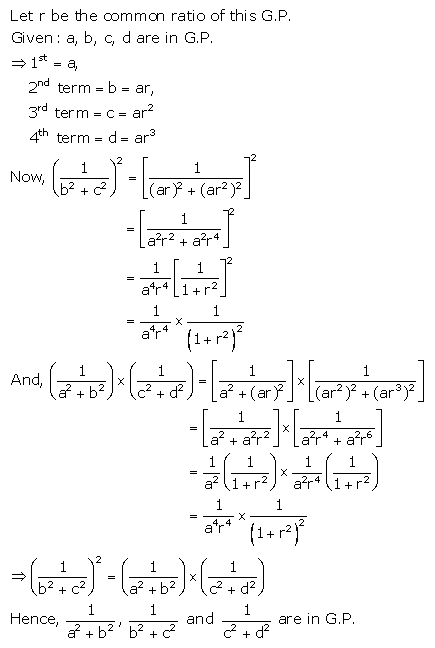

Exercise 11D

Question 1.
Find the sum of G.P. :
(i) 1 + 3 + 9 + 27 + ……….. to 12 terms.
(ii) 0.3 + 0.03 + 0.003 + 0.0003 + …… to 8 terms.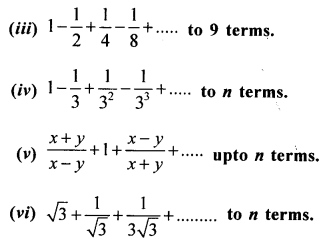

Solution 1(i).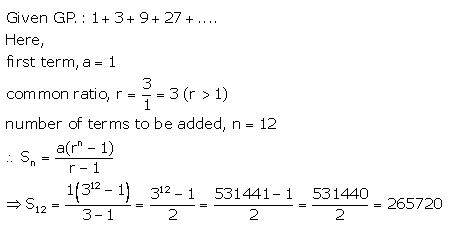

Solution 1(ii).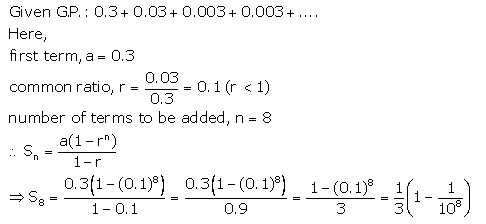

Solution 1(iii).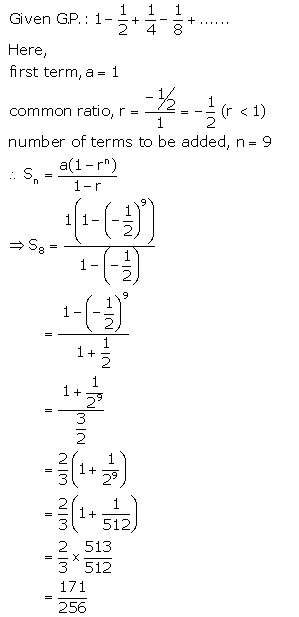

Solution 1(iv).

Solution 1(v).

Solution 1(vi).

Question 2.
How many terms of the geometric progression 1+4 + 16 + 64 + ……… must be added to get sum equal to 5461?
Solution:

Question 3.
The first term of a G.P. is 27 and its 8^th term is 181. Find the sum of its first 10 terms.
Solution: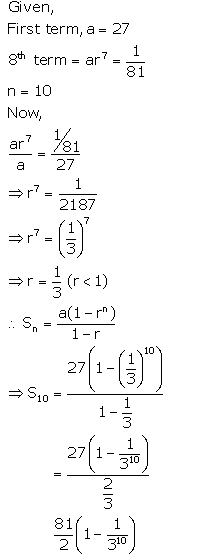

Question 4.
A boy spends ₹ 10 on first day, ₹ 20 on second day, ₹ 40 on third day and so on. Find how much, in all, will he spend in 12 days?
Solution: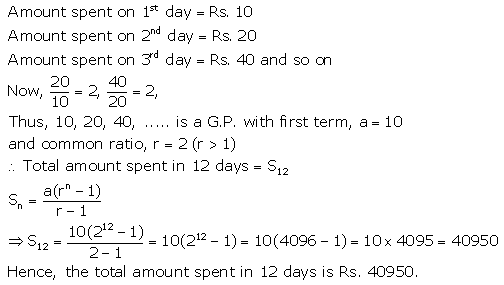

Question 5.
The 4th and the 7th terms of a G.P. are 127 and 1729 respectively. Find the sum of n terms of this G.P.
Solution: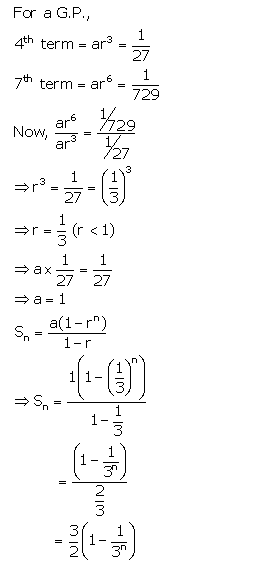

Question 6.
A geometric progression has common ratio = 3 and last term = 486. If the sum of its terms is 728 ; find its first term.
Solution:

Question 7.
Find the sum of G.P. : 3, 6, 12, ……………. 1536.
Solution:

Question 8.
How many terms of the series 2 + 6 + 18 + ………….. must be taken to make the sum equal to 728 ?
Solution:

Question 9.
In a G.P., the ratio between the sum of first three terms and that of the first six terms is 125 : 152.
Find its common ratio.
Solution:

Question 10.
Find how many terms of G.P. 29−13+12 ………. must be added to get the sum equal to 5572?
Solution: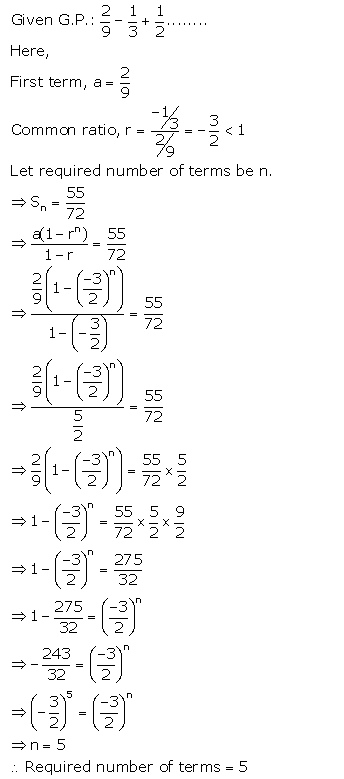

Question 11.
If the sum 1 + 2 + 2² + ………. + 2^n-1 is 255, find the value of n.
Solution:

Question 12.
Find the geometric mean between :
(i) 49 and 94
(ii) 14 and 732
(iii) 2a and 8a³
Solution 12(i).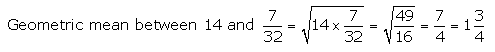

Solution 12(ii).

Solution 12(iii).

Question 13.
The sum of three numbers in G.P. is 3910 and their product is 1. Find the numbers.
Solution:

Question 14.
The first term of a G.P. is -3 and the square of the second term is equal to its 4^th term. Find its 7^th term.
Solution:

Question 15.
Find the 5^th term of the G.P. 52, 1, …..
Solution: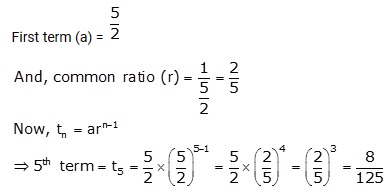

Question 16.
The first two terms of a G.P. are 125 and 25 respectively. Find the 5th and the 6th terms of the G.P.
Solution:

Question 17.
Find the sum of the sequence –13, 1, – 3, 9, …………. upto 8 terms.
Solution:

Question 18.
The first term of a G.P. in 27. If the 8thterm be 181, what will be the sum of 10 terms ?
Solution: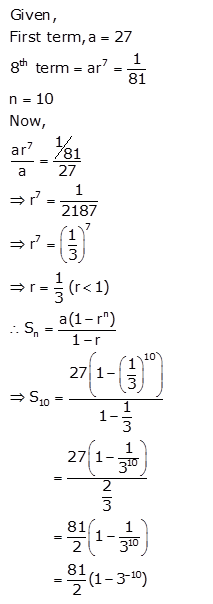

Question 19.
Find a G.P. for which the sum of first two terms is -4 and the fifth term is 4 times the third term.
Solution:

Additional Questions

Question 1.
Find the sum of n terms of the series :
(i) 4 + 44 + 444 + ………
(ii) 0.8 + 0.88 + 0.888 + …………..
Solution 1(i).

Solution 1(ii).

Question 2.
Find the sum of infinite terms of each of the following geometric progression: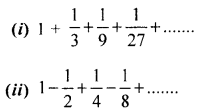


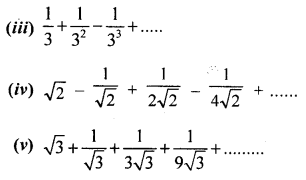
Solution 2(i).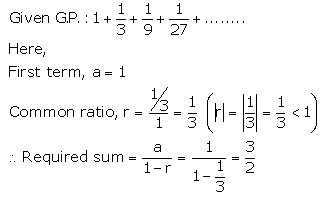

Solution 2(ii).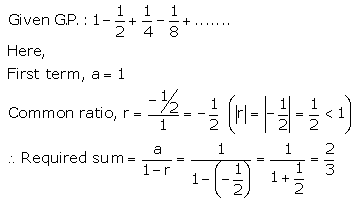

Solution 2(iii).

Solution 2(iv).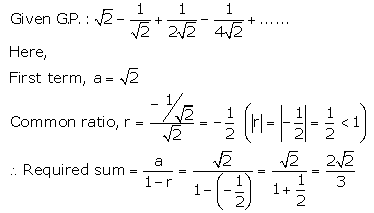

Solution 2(v).

Question 3.
The second term of a G.P. is 9 and sum of its infinite terms is 48. Find its first three terms.
Solution: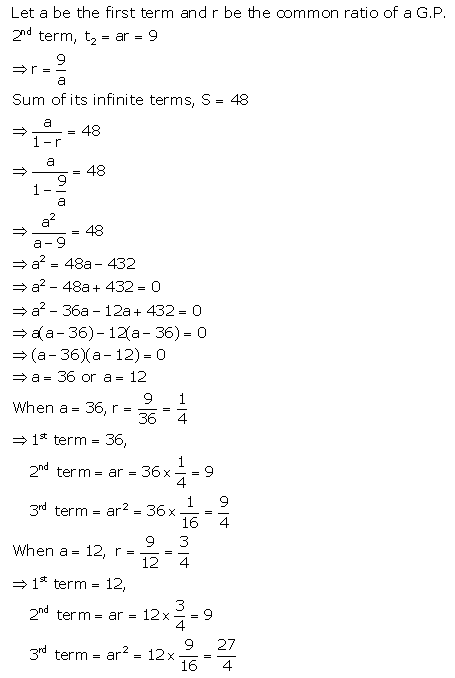

Question 4.
Find three geometric means between 13 and 432.
Solution:

Question 5.
Find :
(i) two geometric means between 2 and 16
(ii) four geometric means between 3 and 96.
(iii) five geometric means between 359 and 4012
Solution 5(i).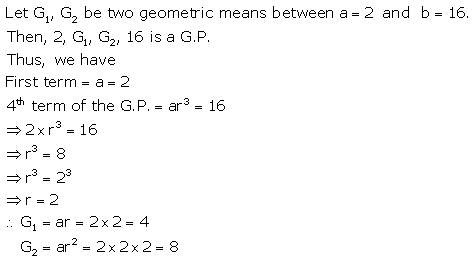

Solution 5(ii).

Solution 5(iii).

Question 6.
The sum of three numbers in G.P. is 3910 and their product is 1. Find the numbers.
Solution:
Sum of three numbers in G.P. = 3910 and their product = 1
Let number be ar, a, ar, then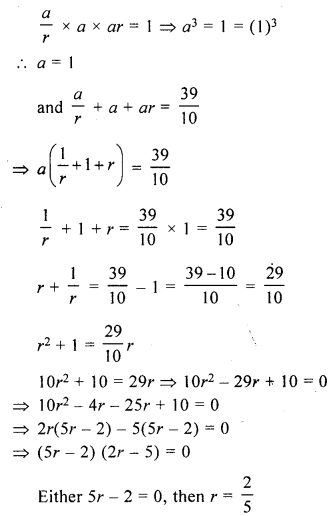

Question 7.
Find the numbers in G.P. whose sum is 52 and the sum of whose product in pairs is 624.
Solution: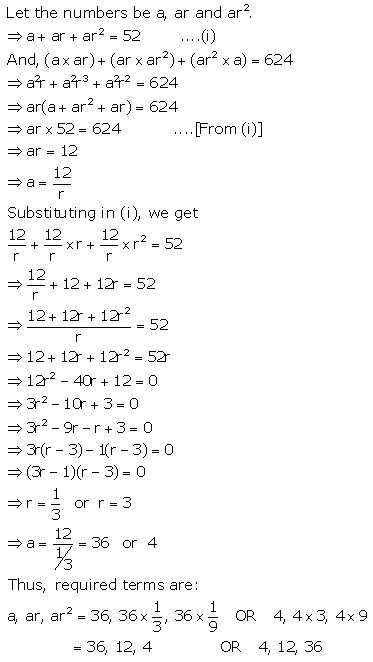

Question 8.
The sum of three numbers in G.P. is 21 and the sum of their squares is 189. Find the numbers.
Solution: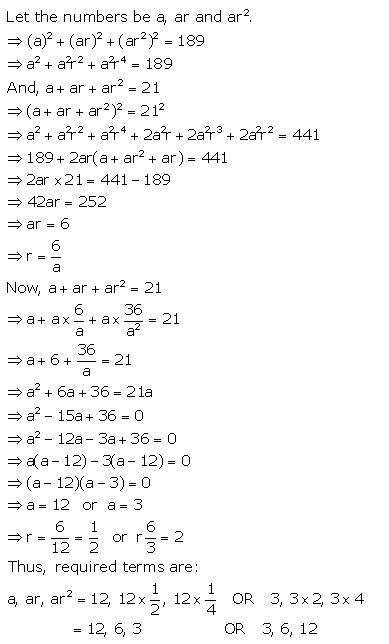

Download PDF

Selina Class 10 ICSE Solutions Mathematics : Chapter 11- Geometric Progression

Download PDF: Selina Class 10 ICSE Solutions Mathematics : Chapter 11- Geometric Progression PDF

Chapterwise Selina Publishers ICSE Solutions for Class 10 Maths :

• Chapter 1 – GST (Goods and Services Tax)
• Chapter 2 – Banking (Recurring Deposit Accounts)
• Chapter 3 -Shares and Dividends
• Chapter 4 – Linear Inequations (in one variable)
• Chapter 5 – Quadratic Equations
• Chapter 6 – Solving Simple Problems (Based on Quadratic Equations)
• Chapter 7 – Ratio and Proportion (Including Properties and Uses)
• Chapter 8 – Remainder and Factor Theorems
• Chapter 9 – Matrices
• Chapter 10- Arithmetic Progression
• Chapter 11- Geometric Progression
• Chapter 12- Reflection
• Chapter 13 – Section and Mid-Point Formula
• Chapter 14- Equation of a Line
• Chapter 15- Similarity
• Chapter 16- Loci (Locus and Its Constructions)
• Chapter 17- Circles
• Chapter 18- Tangents and Intersecting Chords
• Chapter 19- Constructions (Circles)
• Chapter 20- Cylinder, Cone and Sphere
• Chapter 21- Trigonometrical Identities
• Chapter 22- Heights and Distances
• Chapter 23- Graphical Representation
• Chapter 24- Measures of Central Tendency
• Chapter 25- Probability

About Selina Publishers ICSE

Selina Publishers has been serving the students since 1976 and is one of the quality ICSE school textbooks publication houses. Mathematics and Science books for classes 6-10 form the core of our business, apart from certain English and Hindi literature as well as a few primary books. All these books are based upon the syllabus published by the Council for the I.C.S.E. Examinations, New Delhi. The textbooks are composed by a panel of subject experts and vetted by teachers practising in ICSE schools all over the country. Continuous efforts are made in complying with the standards and ensuring lucidity and clarity in content, which makes them stand tall in the industry.