RD Sharma Solutions for Class 6 Maths Chapter 16–Understanding Three-Dimensional Shapes
RD Sharma Solutions for Class 6 Maths Chapter 16–Understanding Three-Dimensional Shapes

Class 6: Maths Chapter 16 solutions. Complete Class 6 Maths Chapter 16 Notes.

RD Sharma Solutions for Class 6 Maths Chapter 16–Understanding Three-Dimensional Shapes

RD Sharma 6th Maths Chapter 16, Class 6 Maths Chapter 16 solutions

Exercise 16.1 page: 16.2

1. Name any four objects from your environment, which have the form of

(i) a cuboid (ii) a cube

Solution:

(i) The objects which have the form of a cuboid are a compass box, a lunch box, a duster and a book.

(ii) The objects which have the form of a cube are a chalk box, a disc, a tissue box and a cubical cabin.

2. Draw a diagram to represent a cuboid. Label its vertices as P, Q, R, S, T, U, V and W. Now write the names of its faces and its edges.

Solution:

The diagram of a cuboid is given below

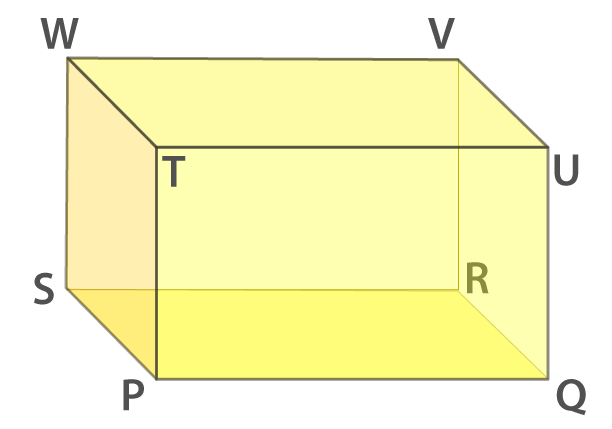
The faces of a cuboid are

The bottom face – PQRS

The top face – TUVW

The back face – WSRV

The left face – TPSW

The right face – UVRQ

The front face – TPQU

The edges of a cuboid are

(PQ, QR, RS, SP), (TU, UV, VW, WT), (WS, SR, RV, VW) and (UV, VR, RQ, QU)

3. Draw a diagram to represent a cube. Label its vertices as A, B, C, D, E, F, G and H. Now write the names of its faces and edges.

Solution:

The diagram of a cube is as follows:

We know that a cube has 6 faces and 12 edges.

The faces of a cube are

ABCD, EFGH, BCGF, ADHE, ABFE and CDHG.

The edges of a cube are

AB, BC, CD, DA, EF, FG, GH, HE, BF, CG, AE and HD

4. Fig. 16.2 represents a cuboid. The lengths of the edges AE, EF, and FG are indicated as l, b and h respectively. Indicated the lengths of all other edges.

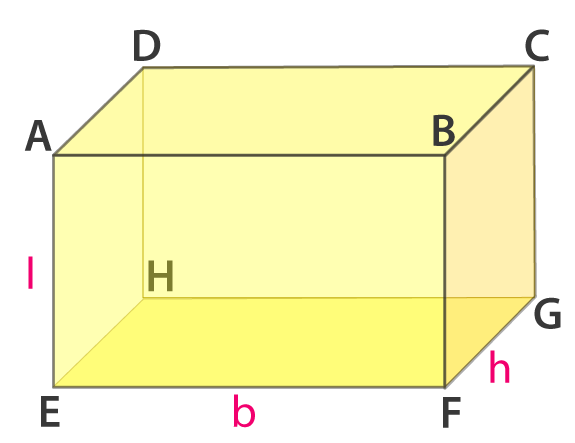
Solution:

It is given that the lengths of the edges AE, EF and FG are indicated as l, b and h respectively. The lengths of all other edges are as follows

AE = DH = BF = CG = l

EF = HG = AB = DC = b

FG = EH = BC = AD = h

5. In Fig. 16.2, if the face EFGH is taken as the base, the name the lateral faces. Also, name the line segment representing the height of the cuboid.

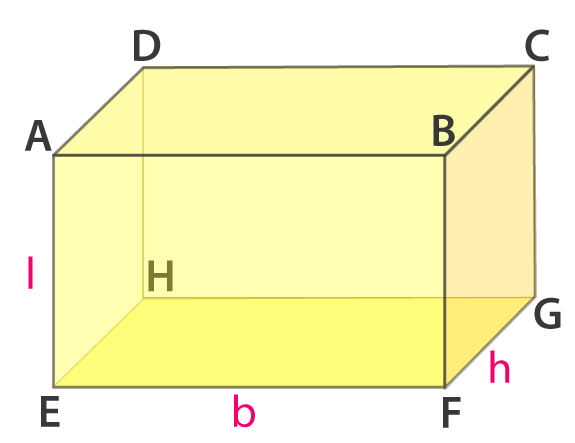
Solution:

The lateral faces for the base EFGH are

AEHD, AEFB, BFGC and DHGC

The line segments representing the height of the cuboid are

AE or DH or BF or CG

6. In Fig. 16.2, name the four diagonals of the cuboid.

Solution:

CE, BH, AG and DF are the four diagonals of a cuboid.

7. In Fig. 16.2, name the

(i) face parallel to BFGC

(ii) faces adjacent to BFGC

(iii) three edges which meet in the vertex G.

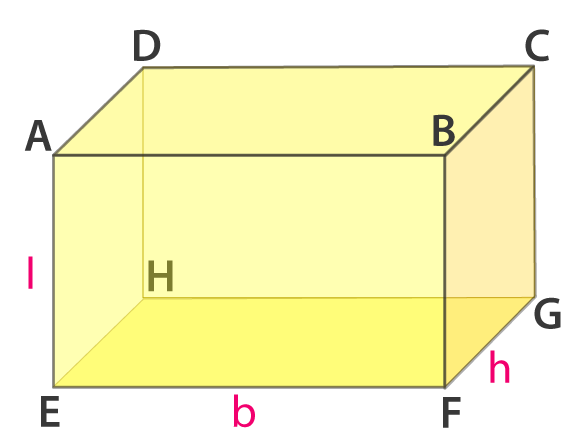
Solution:

(i) AEHD is the face parallel to BFGC

(ii) BCDA, DCGH, ABFE, and EFGH are the faces adjacent to BFGC

(iii) Three edges which meet in the vertex G are CG, GH and GF

8. Fill in the blanks to make the following statements true:

(i) A cuboid has …… vertices.

(ii) A cuboid has …… edges

(iii) A cuboid has ……. Faces.

(iv) The number of lateral faces of a cuboid is ……..

(v) A cuboid all of whose edges are equal is called a …….

(vi) Two adjacent faces of a cuboid meet in a line segment called its …….

(vii) Each edge of a cuboid can be obtained as a line segment in which two …… meet.

(viii) ……edges of a cube (or cuboid) meet at each of its vertices.

(ix) A ……. is a cuboid in which all the six faces are squares.

(x) The three concurrent edges of a cuboid meet at a point called the …… of the cuboid.

Solution:

(i) A cuboid has eight vertices

(ii) A cuboid has twelve edges

(iii) A cuboid has six faces

(iv) The number of lateral faces of a cuboid is four

(v) A cuboid all of whose edges are equal is called a cube

(vi) Two adjacent faces of a cuboid meet in a line segment called its edge

(vii) Each edge of a cuboid can be obtained as a line segment in which two adjacent faces meet

(viii) Three edges of a cube (or cuboid) meet at each of its vertices.

(ix) A cube is a cuboid in which all the six faces are squares

(x) The three concurrent edges of a cuboid meet at a point called the vertex of the cuboid.

9. In each of the following, state if the statement is true (T) or false (F):

(i) Number of faces in a cuboid and the number of faces in a cube are equal.

(ii) A cube has twelve vertices.

Solution:

(i) True

(ii) False

10. For the cuboid shown in Fig. 16.3,

(i) What is the base of this cuboid?

(ii) What are the lateral faces of this cuboid?

(iii) Name one pair of opposite faces. How many pairs of opposite faces are there? Name them.

(iv) Name all the faces of this cuboid which have X as a vertex. Also, name those which have VW as a side

(v) Name the edges of this cuboid which meet at the vertex P. Also, name those faces which meet at this vertex.

Solution:

(i) The base of this cuboid is UVWX

(ii) The lateral faces of this cuboid are UXSP, QVWR, SXWR and UVQP

(iii) One pair of opposite faces among the lateral faces of the base are PQVU and SXWR or UXSP and QVWR. We know that a cuboid has two pairs of opposite faces among the lateral faces of the base.

(iv) The faces of this cuboid which have vertex as X are UVWX, UXSP and SXWR.

The faces having VW as a side are UVWX and QVWR

(v) The edges of this cuboid meeting at the vertex P are UP, PQ and PS.

The faces which meet at this vertex P are PQRS, UPSX and PQVU

11. The dimensions of a cuboid with vertices A, B, C, D, E, F, G and H are as shown in Fig. 16.4.

(i) Which edges are of length 4 cm? Which edges are of length 5 cm?

(ii) Which faces have area equal to 20 cm2?

(iii) Which faces have the largest area? What is this largest area?

(iv) Which faces have a diagonal equal to 5 cm?

(v) What is the area of the base of this cuboid?

(vi) Do all the lateral faces have the same area?

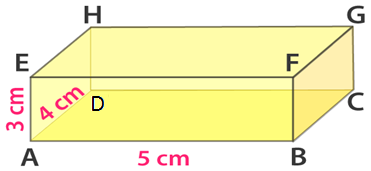
Solution:

(i) The edges of length 4 cm are BC, EH and FG and the edges of length 5 cm are DC, EF and HG

(ii) The faces which have the dimensions of 4 cm and 5 cm i.e. (4 × 5 = 20) have an area equal to 20 cm2. ABCD and EFGH have area equal to 20 cm2

(iii) ABCD and EFGH have the largest area. 20 cm2 is the largest area.

(iv) The faces having the sides 4 cm and 3 cm would have the diagonal of 5 cm and the faces are ADHE and BCGF

(v) The area of the base of this cuboid is 20 cm2

(vi) No all the lateral faces do not have the same area. The two lateral faces have an area 3 × 5 = 15 cm2 and the other have 3 × 4 = 12 cm2

Exercise 16.2 PAGE: 16.9

1. Give two new examples of each of the following three dimensional shapes:

(i) Cone

(ii) Sphere

(iii) Cylinder

(iv) Cuboid

(v)  Pyramid

Solution:

(i) The examples of a cone are a funnel and a school bell.

(ii) The examples of a sphere are tennis ball and a model of a globe.

(iii) The examples of a cylinder are drink cans and delivering pipes for a water and gas.

(iv) The examples of cuboid are a match box and brick.

(v) The examples of pyramid are a paper- weight and a tower like the Eiffel tower.

2. What is the shape of:

(i) your instrument box

(ii) a brick

(iii) a match box

(iv) a rod- roller

(v) a sweet laddoo

Solutions:

(i) Your instrument box – cuboid shape

(ii) A brick – cuboid shape

(iii) A match box – cuboid shape

(iv) A road – roller – cylinder shape

(v) A sweet laddoo – sphere shape

Objective Type Questions page: 16.9

Mark the correct alternative in each of the following:

1. Total number of faces of a cuboid is

(a) 4 (b) 6 (c) 8 (d) 12

Solution:

The option (b) is the correct answer.

Total number of faces of a cuboid is 6.

2. Total number of edges of a cuboid is

(a) 4 (b) 6 (c) 8 (d) 12

Solution:

The option (d) is the correct answer.

Total number of edges of a cuboid is 12.

3. Number of vertices of a cuboid is

(a) 4 (b) 6 (c) 8 (d) 10

Solution:

The option (c) is the correct answer.

Number of vertices of a cuboid is 8.

4. Which one of the following is an example of a cuboid?

(a) a dice (b) a football (c) a gas pipe (d) an ice-cream cone

Solution:

The option (a) is the correct answer.

Example of a cuboid is a dice.

5. A brick is an example of a

(a) cube (b) cuboid (c) prism (d) cylinder

Solution:

The option (b) is the correct answer.

A brick is an example of a cuboid.

6. A gas pipe is an example of a

(a) cone (b) a cylinder (c) cube (d) sphere

Solution:

The option (b) is the correct answer.

A gas pipe is an example of a cylinder.

7. If the base radius and height of a right circular cone are 3 cm and 4 cm in lengths, then the slant height is

(a) 5 cm (b) 2 cm (c) 25 cm (d) 6 cm

Solution:

The option (a) is the correct answer.

If the base radius and height of a right circular cone are 3 cm and 4 cm in lengths, then the slant height is 5 cm.

Slant height = √32 + 42 = √25 = 5 cm

8. The number of faces of a triangular pyramid is

(a) 3 (b) 4 (c) 6 (d) 8

Solution:

The option (b) is the correct answer.

The number of faces of a triangular pyramid is 4.

9. The number of edges of a triangular pyramid is

(a) 3 (b) 4 (c) 6 (d) 8

Solution:

The option (c) is the correct answer.

The number of edges of a triangular pyramid is 6.

10. A tetrahedron is a pyramid whose base is a

(a) triangle (b) square (c) rectangle (d) quadrilateral

Solution:

The option (a) is the correct answer.

A tetrahedron is a pyramid whose base is a triangle.

RD Sharma Solutions for Class 6 Maths Chapter 16: Download PDF

RD Sharma Solutions for Class 6 Maths Chapter 16–Understanding Three-Dimensional Shapes

Download PDF: RD Sharma Solutions for Class 6 Maths Chapter 16–Understanding Three-Dimensional Shapes PDF

Chapterwise RD Sharma Solutions for Class 6 Maths :

About RD Sharma

RD Sharma isn’t the kind of author you’d bump into at lit fests. But his bestselling books have helped many CBSE students lose their dread of maths. Sunday Times profiles the tutor turned internet star
He dreams of algorithms that would give most people nightmares. And, spends every waking hour thinking of ways to explain concepts like ‘series solution of linear differential equations’. Meet Dr Ravi Dutt Sharma — mathematics teacher and author of 25 reference books — whose name evokes as much awe as the subject he teaches. And though students have used his thick tomes for the last 31 years to ace the dreaded maths exam, it’s only recently that a spoof video turned the tutor into a YouTube star.

R D Sharma had a good laugh but said he shared little with his on-screen persona except for the love for maths. “I like to spend all my time thinking and writing about maths problems. I find it relaxing,” he says. When he is not writing books explaining mathematical concepts for classes 6 to 12 and engineering students, Sharma is busy dispensing his duty as vice-principal and head of department of science and humanities at Delhi government’s Guru Nanak Dev Institute of Technology.

Read More