NCERT Exemplar Class 7 Maths Chapter 8: Rationals Numbers. NCERT Exemplar Solutions for Class 7 Maths Chapter 8 Rationals Numbers prepare students for their Class 7 exams thoroughly.
Maths problems and solutions for the Class 7 pdf are provided here which are similar to the questions being asked in the previous year’s board.
Contents
NCERT Exemplar Class 7 Maths Chapter 8: Rationals Numbers
Class 7: Maths Chapter 8 solutions. Complete Class 7 Maths Chapter 8 Notes.
Main Concepts and Results
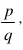

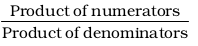

A number that can be expressed in the form where p and q are integers and is called a rational number.
All integers and fractions are rational numbers.
If the numerator and denominator of a rational number are multiplied or divided by a non-zero integer, we get a rational number which is said to be equivalent to the given rational number.
Rational numbers are classified as positive, zero or negative rational numbers. When the numerator and denominator both are positive integers or both are negative integers, it is a positive rational number.
When either the numerator or the denominator is a negative integer, it is a negative rational number.
The number 0 is neither a positive nor a negative rational number.
There are unlimited number of rational numbers between two rational numbers.
A rational number is said to be in the standard form, if its denominator is a positive integer and the numerator and denominator have no common factor other than 1.
Two rational numbers with the same denominator can be added by adding their numerators, keeping with the same denominator.
Two rational numbers with different denominators are added by first taking the LCM of the two denominators and then converting both the rational numbers to their equivalent forms having the LCM as the denominator and adding them as above.
While subtracting two rational numbers, we add the additive inverse of the rational number to be subtracted to the other rational number.
Product of rational numbers = .
The reciprocal of a non-zero rational number
To divide one rational number by the other non-zero rational number, we multiply the first rational number by the reciprocal of the other.
Solved Examples























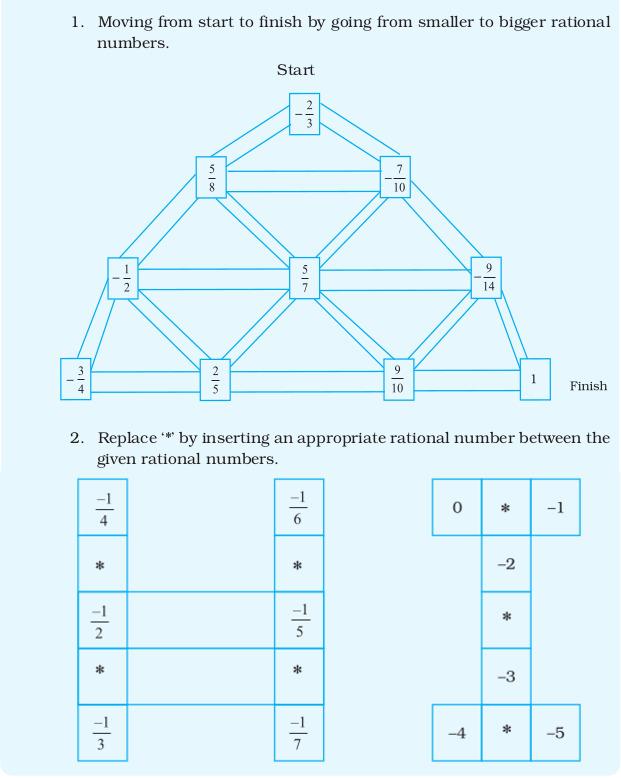
Multiple Choice Questions

Fill in the Blanks Type Questions

True False Type Questions

Other Important Type Questions

Application


Click here to download NCERT Exemplar Class 7 Maths for Unit 8 Rational Numbers.
Answers





