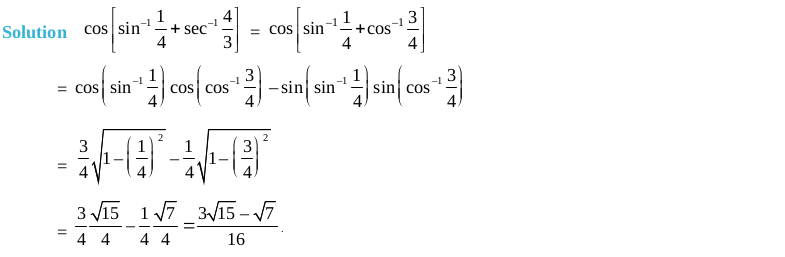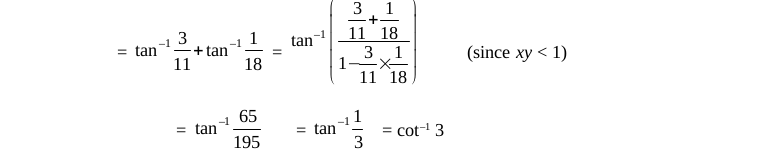NCERT Exemplar Class 12 Maths Chapter 2: Inverse Trigonometric Function. NCERT Exemplar Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Function prepare students for their Class 12 exams thoroughly.
Maths problems and solutions for the Class 12 pdf are provided here which are similar to the questions being asked in the previous year’s board.
Contents
- 1 NCERT Exemplar Class 12 Maths Chapter 2: Inverse Trigonometric Function
- 1.1 Short Answer Type Questions (Solved Examples)
- 1.2
- 1.3 Long Answer Type Questions (Solved Examples)
- 1.4
- 1.5
- 1.6 Objective type questions (Solved Examples)
- 1.7 Short Answer Type Questions (Exercise)
- 1.8 Long Answer Type Questions (Exercise)
- 1.9 Multiple Choice Questions (Exercise)
- 1.10 Fill In Blanks Type Questions (Exercise)
- 1.11 True or False Statements Type Questions (Exercise)
- 2 Answers
NCERT Exemplar Class 12 Maths Chapter 2: Inverse Trigonometric Function
2.1 Overview
2.1.1 Inverse function
Inverse of a function ‘f ’ exists, if the function is one-one and onto, i.e, bijective. Since trigonometric functions are many-one over their domains, we restrict their domains and co-domains in order to make them one-one and onto and then find their inverse. The domains and ranges (principal value branches) of inverse trigonometric functions are given below:

Notes:
(i) The symbol sin-1x should not be confused with (sinx)-1 . Infact sin-1x is an angle, the value of whose sine is x, similarly for other trigonometric functions.
(ii) The smallest numerical value, either positive or negative, of θ is called the principal value of the function.
(iii) Whenever no branch of an inverse trigonometric function is mentioned, we mean the principal value branch. The value of the inverse trigonometic function which lies in the range of principal branch is its principal value.
2.1.2 Graph of an inverse trigonometric function
The graph of an inverse trigonometric function can be obtained from the graph of original function by interchanging x-axis and y-axis, i.e, if (a, b) is a point on the graph of trigonometric function, then (b, a) becomes the corresponding point on the graph of its inverse trigonometric function.
It can be shown that the graph of an inverse function can be obtained from the corresponding graph of original function as a mirror image (i.e., reflection) along the line y = x.
2.1.3 Properties of inverse trigonometric functions


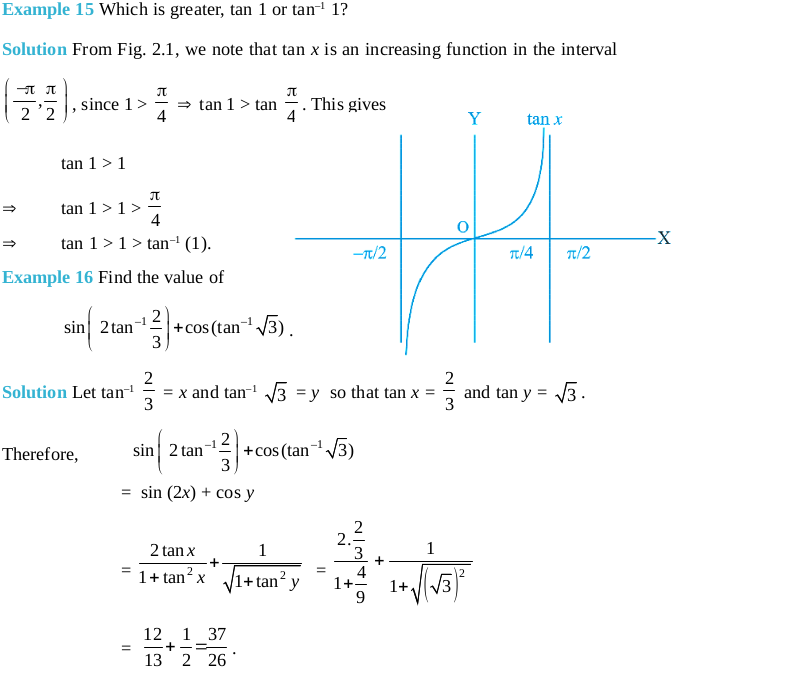
Short Answer Type Questions (Solved Examples)


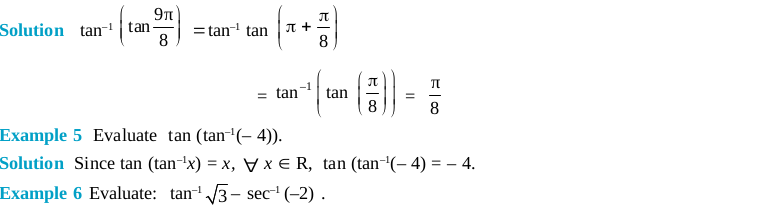



Long Answer Type Questions (Solved Examples)
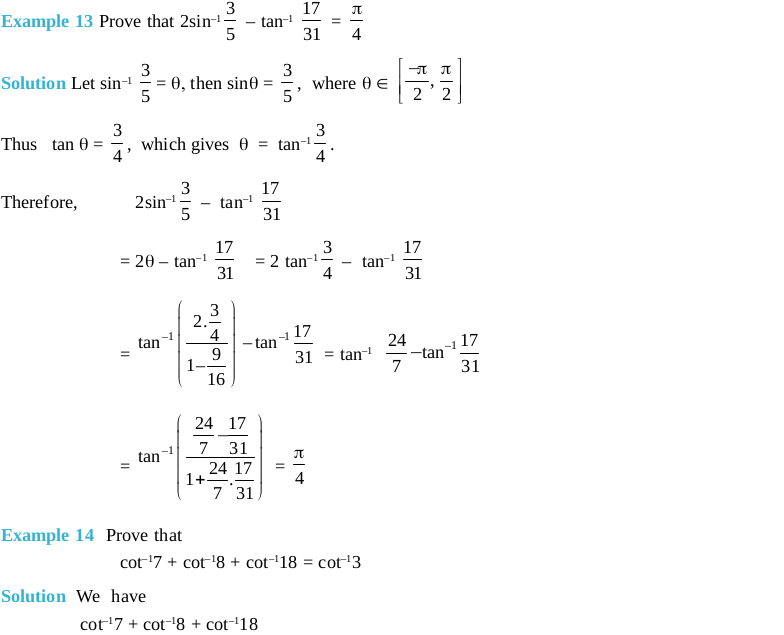
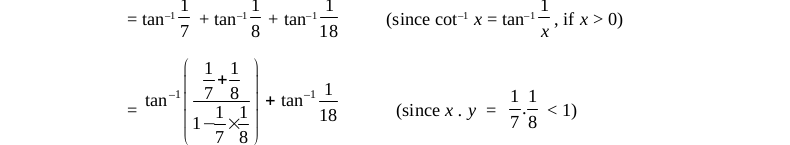

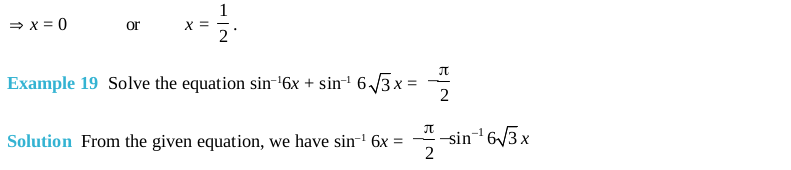
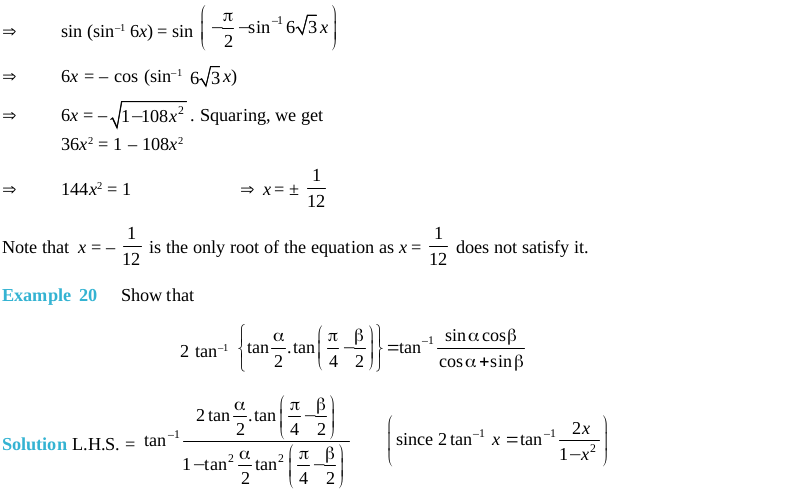
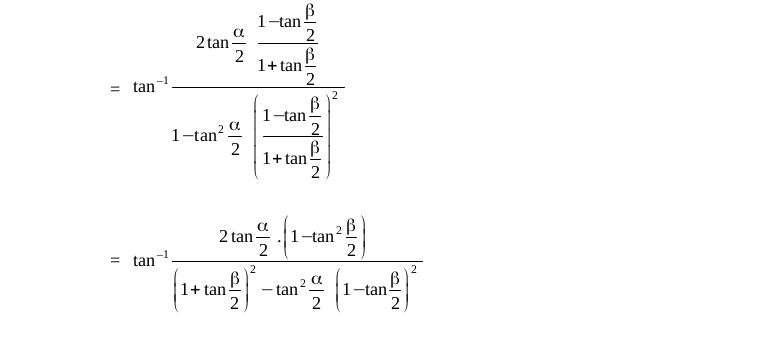

Objective type questions (Solved Examples)






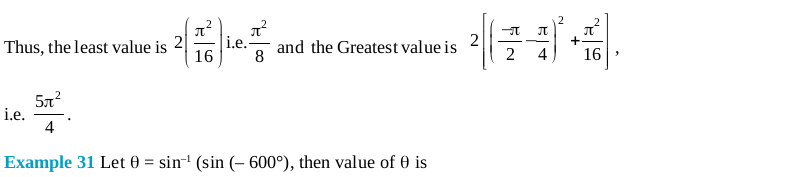

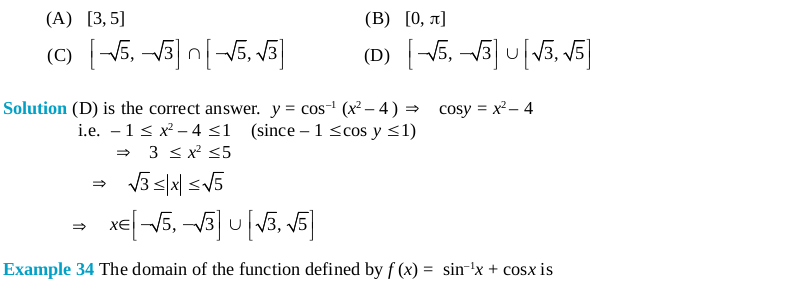

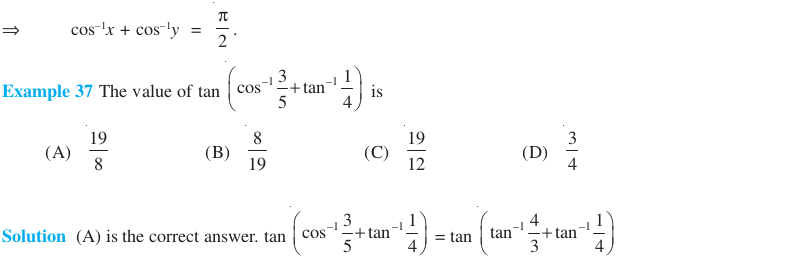
Click Here to download NCERT Exemplar Class 12 Maths Unit 2 Inverse Trigonometric Function.

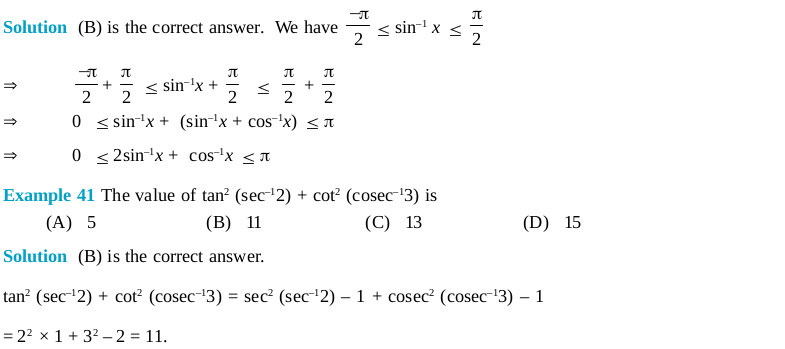
Short Answer Type Questions (Exercise)

Long Answer Type Questions (Exercise)

Multiple Choice Questions (Exercise)
Click Here to download NCERT Exemplar Class 12 Maths Unit 2 Inverse Trigonometric Function.
Fill In Blanks Type Questions (Exercise)

True or False Statements Type Questions (Exercise)

Answers


Class 12: Maths Chapter 2 solutions. Complete Class 12 Maths Chapter 2 Notes.