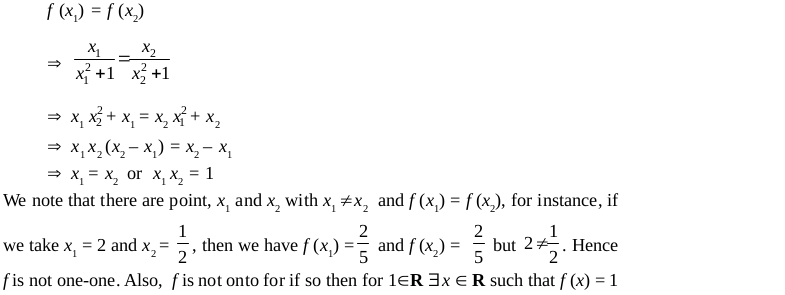NCERT Exemplar Class 12 Maths Chapter 1: Relations and Functions. NCERT Exemplar Solutions for Class 12 Maths Chapter 1 Relations and Functions prepare students for their Class 12 exams thoroughly.
Maths problems and solutions for the Class 12 pdf are provided here which are similar to the questions being asked in the previous year's board.
NCERT Exemplar Class 12 Maths Chapter 1: Relations and Functions
Class 12: Maths Chapter 1 solutions. Complete Class 12 Maths Chapter 1 Notes.
1.1 Overview
1.1.1 Relation
A relation R from a non-empty set A to a non empty set B is a subset of the Cartesian product A × B. The set of all first elements of the ordered pairs in a relation R from a set A to a set B is called the domain of the relation R. The set of all second elements in a relation R from a set A to a set B is called the range of the relation R. The whole set B is called the codomain of the relation R. Note that range is always a subset of codomain.
1.1.2 Types of Relations
A relation R in a set A is subset of A × A. Thus empty set φ and A × A are two extreme relations.
(i) A relation R in a set A is called empty relation, if no element of A is related to any element of A, i.e., R = φ ⊂ A × A.
(ii) A relation R in a set A is called universal relation, if each element of A is related to every element of A, i.e., R = A × A.
(iii) A relation R in A is said to be reflexive if aRa for all a∈A, R is symmetric if aRb ⇒ bRa, ∀ a, b ∈ A and it is said to be transitive if aRb and bRc ⇒ aRc ∀ a, b, c ∈ A. Any relation which is reflexive, symmetric and transitive is called an equivalence relation.
Note: An important property of an equivalence relation is that it divides the set into pairwise disjoint subsets called equivalent classes whose collection is called a partition of the set. Note that the union of all equivalence classes gives the whole set.
1.1.3 Types of Functions
(i) A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct i.e.,
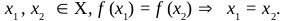
(ii) A function f : X → Y is said to be onto (or surjective), if every element of Y is the image of some element of X under f, i.e., for every y ∈ Y there exists an element x ∈ X such that f (x) = y.
(iii) A function f : X → Y is said to be one-one and onto (or bijective), if f is both one- one and onto.
1.1.4 Composition of Functions
(i) Let f : A → B and g : B → C be two functions. Then, the composition of f and g, denoted by g o f, is defined as the function g o f : A → C given by g o f (x) = g (f (x)), ∀ x ∈ A.
(ii) If f : A → B and g : B → C are one-one, then g o f : A → C is also one-one
(iii) If f : A → B and g : B → C are onto, then g o f : A → C is also onto. However, converse of above stated results (ii) and (iii) need not be true. Moreover, we have the following results in this direction.
(iv) Let f : A → B and g : B → C be the given functions such that g o f is one-one. Then f is one-one.
(v) Let f : A → B and g : B → C be the given functions such that g o f is onto. Then g is onto
1.1.5 Invertible Function
1.1.6 Binary Operations
(i) A binary operation * on a set A is a function * : A × A → A. We denote * (a, b) by a * b.
(ii) A binary operation * on the set X is called commutative, if a * b = b * a for every a, b ∈ X.
(iii) A binary operation * : A × A → A is said to be associative if (a * b) * c = a * (b * c), for every a, b, c ∈ A.
(iv) Given a binary operation * : A × A → A, an element e ∈ A, if it exists, is called identity for the operation *, if a * e = a = e * a, ∀ a ∈ A.
(v) Given a binary operation * : A × A → A, with the identity element e in A, an element a ∈ A, is said to be invertible with respect to the operation *, if there exists an element b in A such that a * b = e = b * a and b is called the inverse of a and is denoted by a-1 .
Short Answer Type Questions (Solved Examples)
Long Answer Type Questions (Solved Examples)
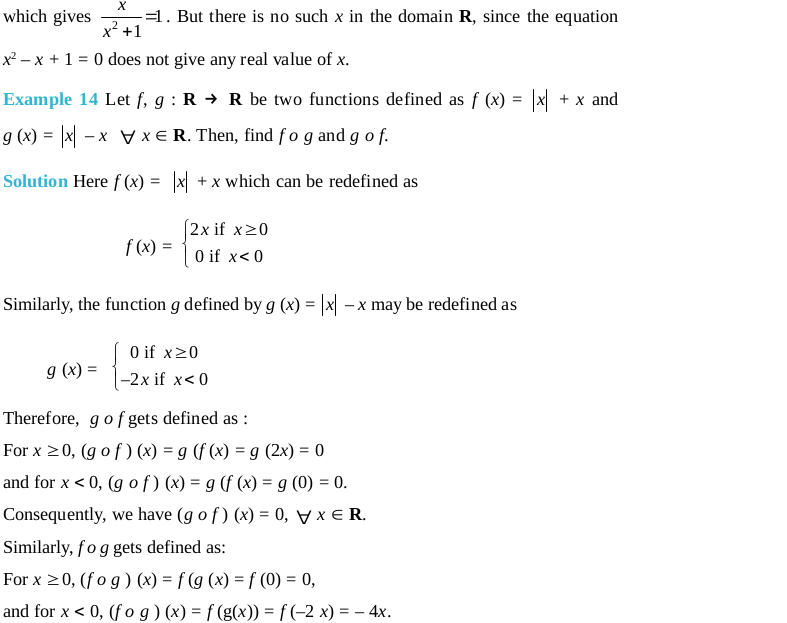
Objective Type Questions (Solved Examples)
Fill in the Blanks Type Questions (Solved Examples)
True or False Statements Type Questions (Solved Examples)
Short Answer Type Questions (Exercise)
Long Answer Type Questions (Exercise)
Multiple Choice Questions
Fill In Blanks Type Questions
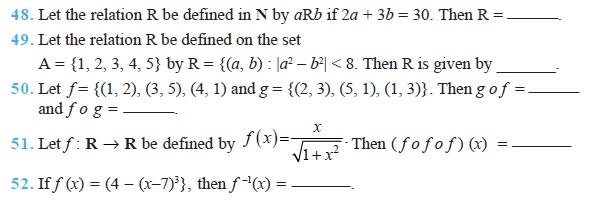
True or False Statements Type Questions
Click Here to download NCERT Exemplar Class 12 Maths Unit 1 Relations and Function.
Answers
