Class 9: Maths Chapter 4 solutions. Complete Class 9 Maths Chapter 4 Notes.
Contents
ML Aggarwal Solutions for Class 9 Maths Chapter 4- Factorization
ML Aggarwal 9th Maths Chapter 4, Class 9 Maths Chapter 4 solutions
Exercise 4.1
Factorise the following (1 to 9):
1. (i) 8xy3 + 12x2y2
Solution:-
8xy3 + 12x2y2
Take out common in both terms,
Then, 4xy2 (2y + 3x)
Therefore, HCF of 8xy3 and 12x2y2 is 4xy2.
(ii) 15 ax3 – 9ax2
Solution:-
15 ax3 – 9ax2
Take out common in both terms,
Then, 3ax2 (5x – 3)
Therefore, HCF of 15 ax3 and 9ax2 is 3ax2.
2.
(i) 21py2 – 56py
Solution:-
21py2 – 56py
Take out common in both terms,
Then, 7py (3y – 8)
Therefore, HCF of 21py2 and 56py is 7py.
(ii) 4x3 – 6x2
Solution:-
4x3 – 6x2
Take out common in both terms,
Then, 2x2 (2x – 3)
Therefore, HCF of 4x3 and 6x2 is 2x2.
3.
(i) 2πr2 – 4πr
Solution:-
2πr2 – 4πr
Take out common in both terms,
Then, 2πr (r – 2)
Therefore, HCF of 2πr2 and 4πr is 2πr.
(ii) 18m + 16n
Solution:-
18m + 16n
Take out common in both terms,
Then, 2 (9m – 8n)
Therefore, HCF of 18m and 16n is 2.
4.
(i) 25abc2 – 15a2b2c
Solution:-
25abc2 – 15a2b2c
Take out common in both terms,
Then, 5abc (5c – 3ab)
Therefore, HCF of 25abc2 and 15a2b2c is 5abc.
(ii) 28p2q2r – 42pq2r2
Solution:-
28p2q2r – 42pq2r2
Take out common in both terms,
Then, 14pq2r (2p – 3r)
Therefore, HCF of 28p2q2r and 42pq2r2 is 14pq2r.
5.
(i) 8x3 – 6x2 + 10x
Solution:-
8x3 – 6x2 + 10x
Take out common in both terms,
Then, 2x(4x2 – 3x + 5)
Therefore, HCF of 8x3, 6x2 and 10x is 2x.
(ii) 14mn + 22m – 62p
Solution:-
14mn + 22m – 62p
Take out common in both terms,
Then, 2 (7mn + 11m – 31p)
Therefore, HCF of 14mn, 22m and 62p is 2.
6.
(i) 18p2q2 – 24pq2 + 30p2q
Solution:-
18p2q2 – 24pq2 + 30p2q
Take out common in both terms,
Then, 6pq (3pq – 4q + 5p)
Therefore, HCF of 18p2q2, 24pq2 and 30p2q is 6pq.
(ii) 27a3b3 – 18a2b3 + 75a3b2
Solution:-
27a3b3 – 18a2b3 + 75a3b2
Take out common in both terms,
Then, 3a2b2 (9a – 6b + 25a)
Therefore, HCF of 27a3b3, 18a2b3 and 75a3b2 is 3a2b2.
7.
(i) 15a (2p – 3q) – 10b (2p – 3q)
Solution:-
15a (2p – 3q) – 10b (2p – 3q)
Take out common in both terms,
Then, 5(2p – 3q) [3a – 2b]
Therefore, HCF of 15a (2p – 3q) and 10b (2p – 3q) is 5(2p – 3q).
(ii) 3a(x2 + y2) + 6b (x2 + y2)
Solution:-
3a(x2 + y2) + 6b (x2 + y2)
Take out common in all terms,
Then, 3(x2 + y2) (a + 2b)
Therefore, HCF of 3a(x2 + y2) and 6b (x2 + y2) is 3(x2 + y2).
8.
(i) 6(x + 2y)3 + 8(x + 2y)2
Solution:-
6(x + 2y)3 + 8(x + 2y)2
Take out common in all terms,
Then, 2(x + 2y)2 [3(x + 2y) + 4]
Therefore, HCF of 6(x + 2y)3 and 8(x + 2y)2 is 2(x + 2y)2.
(ii) 14(a – 3b)3 – 21p(a – 3b)
Solution:-
14(a – 3b)3 – 21p(a – 3b)
Take out common in all terms,
Then, 7(a – 3b) [2(a – 3b)2 – 3p]
Therefore, HCF of 14(a – 3b)3 and 21p(a – 3b) is 7(a – 3b).
9.
(i) 10a(2p + q)3 – 15b (2p + q)2 + 35 (2p + q)
Solution:-
10a(2p + q)3 – 15b (2p + q)2 + 35 (2p + q)
Take out common in all terms,
Then, 5(2p + q) [2a (2p + q)2 – 3b (2p + q) + 7]
Therefore, HCF of 10a(2p + q)3, 15b (2p + q)2 and 35 (2p + q) is 5(2p + q).
(ii) x(x2 + y2 – z2) + y(-x2 – y2 + z2) – z (x2 + y – z2)
Solution:-
x(x2 + y2 – z2) + y(-x2 – y2 + z2) – z (x2 + y – z2)
Take out common in all terms,
Then, (x2 + y2 – z2) [x – y – z]
Therefore, HCF of x(x2 + y2 – z2), y(-x2 – y2 + z2) and z (x2 + y – z2) is (x2 + y2 – z2)
Exercise 4.2
Factorise the following (1 to 13):
1.
(i) x2 + xy – x – y
Solution:-
x2 + xy – x – y
Take out common in all terms,
x(x + y) – 1(x + y)
(x + y) (x – 1)
(ii) y2 – yz – 5y + 5z
Solution:-
y2 – yz – 5y + 5z
Take out common in all terms,
y(y – z) – 5(y – z)
(y – z) (y – 5)
2.
(i) 5xy + 7y – 5y2 – 7x
Solution:-
5xy – 7x – 5y2 + 7y
Take out common in all terms,
x(5y – 7) – y(5y – 7)
(5y – 7) (x – y)
(ii) 5p2 – 8pq – 10p + 16q
Solution:-
5p2 – 8pq – 10p + 16q
Take out common in all terms,
p(5p – 8q) – 2(5p – 8q)
(5p – 8q) (p – 2)
3.
(i) a2b – ab2 + 3a – 3b
Solution:-
a2b – ab2 + 3a – 3b
Take out common in all terms,
ab(a – b) + 3(a – b)
(a – b) (ab + 3)
(ii) x3 – 3x2 + x – 3
Solution:-
x3 – 3x2 + x – 3
Take out common in all terms,
x2 (x – 3) + 1(x – 3)
(x – 3) (x2 + 1)
4.
(i) 6xy2 – 3xy – 10y + 5
Solution:-
6xy2 – 3xy – 10y + 5
Take out common in all terms,
3xy(2y – 1) – 5(2y – 1)
(2y – 1) (3xy – 5)
(ii) 3ax – 6ay – 8by + 4bx
Solution:-
3ax – 6ay – 8by + 4bx
Take out common in all terms,
3a(x – 2y) + 4b (x – 2y)
(x – 2y) (3a + 4b)
5.
(i) 1 – a – b + ab
Solution:-
1 – a – b + ab
Take out common in all terms,
1(1 – a) – b(1 – a)
(1 – a) (1 – b)
(ii) a(a – 2b – c) + 2bc
Solution:-
a(a – 2b – c) + 2bc
Above question can be written as,
a2 – 2ab – ac + 2bc
Take out common in all terms,
a(a – 2b) – c(a + 2b)
(a – 2b) (a – c)
6.
(i) x2 + xy (1 + y) + y3
Solution:-
x2 + xy (1 + y) + y3
Above question can be written as,
x2 + xy + xy2 + y3
Take out common in all terms,
x(x + y) + y2(x + y)
(x + y) (x + y2)
(ii) y2 – xy (1 – x) – x3
Solution:-
y2 – xy (1 – x) – x3
Above question can be written as,
y2 – xy + x2y – x3
Take out common in all terms,
y(y – x) + x2 (y – x)
(y – x) (y + x2)
7.
(i) ab2 + (a – 1)b – 1
Solution:-
ab2 + (a – 1)b – 1
Above question can be written as,
ab2 + ab – b – 1
Take out common in all terms,
ab(b + 1) – 1(b + 1)
(b + 1) (ab – 1)
(ii) 2a – 4b – xa + 2bx
Solution:-
2a – 4b – xa + 2bx
Take out common in all terms,
2(a – 2b) – x(a – 2b)
(a – 2b) (2 – x)
8.
(i) 5ph – 10qk + 2rph – 4qrk
Solution:-
5ph – 10qk + 2rph – 4qrk
Re-arranging the given question we get,
5ph + 2rph – 10qk – 4qrk
Take out common in all terms,
ph(5 + 2r) – 2qk(5 + 2r)
(5 + 2r) (ph – 2qk)
(ii) x2 – x(a + 2b) + 2ab
Solution:-
x2 – x(a + 2b) + 2ab
Above question can be written as,
x2 – xa – 2xb + 2ab
Take out common in all terms,
x(x – a) – 2b(x – a)
(x – a) (x – 2b)
9.
(i) ab(x2 + y2) – xy(a2 + b2)
Solution:-
ab(x2 + y2) – xy(a2 + b2)
Above question can be written as,
abx2 + aby2 – xya2 – xyb2
Re-arranging the above we get,
abx2 – xyb2 + aby2 – xya2
Take out common in all terms,
bx(ax – by) + ay(by – ax)
bx(ax – by) – ay (ax – by)
(ax – by) (bx – ay)
(ii) (ax + by)2 + (bx – ay)2
Solution:-
By expanding the give question, we get,
(ax)2 + (by)2 + 2axby + (bx)2 + (ay)2 – 2bxay
a2x2 + b2y2 + b2x2 + a2y2
Re-arranging the above we get,
a2x2 + a2y2 + b2y2 + b2x2
Take out common in all terms,
a2 (x2 + y2) + b2 (x2 + y2)
(x2 + y2) (a2 + b2)
10.
(i) a3 + ab(1 – 2a) – 2b2
Solution:-
a3 + ab(1 – 2a) – 2b2
Above question can be written as,
a3 + ab – 2a2b – 2b2
Re-arranging the above we get,
a3 – 2a2b + ab – 2b2
Take out common in all terms,
a2(a – 2b) + b(a – 2b)
(a – 2b) (a2 + b)
(ii) 3x2y – 3xy + 12x – 12
Solution:-
3x2y – 3xy + 12x – 12
Take out common in all terms,
3xy(x – 1) + 12(x – 1)
(x – 1) (3xy + 12)
11. a2b + ab2 –abc – b2c + axy + bxy
Solution:-
a2b + ab2 –abc – b2c + axy + bxy
Re-arranging the above we get,
a2b – abc + axy + ab2 – b2c + bxy
Take out common in all terms,
a(ab – bc + xy) + b(ab – bc + xy)
(a + b) (ab – bc + xy)
12. ax2 – bx2 + ay2 – by2 + az2 – bz2
Solution:-
ax2 – bx2 + ay2 – by2 + az2 – bz2
Re-arranging the above we get,
ax2 + ay2 + az2 – bx2 – by2 – bz2
Take out common in all terms,
a(x2 + y2 + z2) – b(x2 + y2 + z2)
(x2 + y2 + z2) (a – b)
13. x – 1 – (x – 1)2 + ax – a
Solution:-
x – 1 – (x – 1)2 + ax – a
By expanding the above we get,
X – 1 – (x2 + 1 – 2x) + ax – a
x – 1 – x2 -1 + 2x + ax – a
2x – x2 + ax – 2 + x – a
Take out common in all terms,
x(2 – x + a) – 1(2 – x + a)
(2 – x + a) (x – 1)
Exercise 4.3
Factorise the following (1 to 17):
1. 4x2 – 25y2
Solution:-
We know that, a2 – b2 = (a + b) (a – b)
So, (2x)2 – (5y)2
Then, (2x + y) (2x – 5y)
(ii) 9x2 – 1
Solution:-
We know that, a2 – b2 = (a + b) (a – b)
So, (3x)2 – 12
Then, (3x + 1) (3x – 1)
2.
(i) 150 – 6a2
Solution:-
150 – 6a2
Take out common in all terms,
6(25 – a2)
6(52 – a2)
We know that, a2 – b2 = (a + b) (a – b)
So, 6(5 + a) (5 – a)
(ii) 32x2 – 18y2
Solution:-
32x2 – 18y2
Take out common in all terms,
2(16x2 – 9y2)
2((4x)2 – (3y)2)
We know that, a2 – b2 = (a + b) (a – b)
2(4x + 3y) (4x – 3y)
3.
(ii) (x – y)2 – 9
Solution:-
(x – y)2 – 9
(x – y)2 – 32
We know that, a2 – b2 = (a + b) (a – b)
(x – y + 3) (x – y – 3)
(ii) 9(x + y)2 – x2
Solution:-
9[(x + y)2 – x2]
We know that, a2 – b2 = (a + b) (a – b)
9[(x + y + x) (x + y – x)]
So, 9(2x + y) y
9y(2x + y)
4.
(i) 20x2 – 45y2
Solution:-
20x2 – 45y2
Take out common in all terms,
5(4x2 – 9y2)
5((2x)2 – (3y)2)
We know that, a2 – b2 = (a + b) (a – b)
5(2x + 3y) (2x – 3y)
(ii) 9x2 – 4(y + 2x)2
Solution:-
9x2 – 4(y + 2x)2
Above question can be written as,
(3x)2 – [2(y + 2x)]2
(3x)2 – (2y + 4x)2
We know that, a2 – b2 = (a + b) (a – b)
(3x + 2y + 4x) (3x – 2y – 4x)
(7x + 2y) (-x – 2y)
5.
(i) 2(x – 2y)2 – 50y2
Solution:-
2(x – 2y)2 – 50y2
Take out common in all terms,
2[(x – 2y)2 – 25y2]
2[(x – 2y)2 – (5y)2]
We know that, a2 – b2 = (a + b) (a – b)
2[(x – 2y + 5y) (x – 2y – 5y)]
2[(x + 3y) (x – 7y)]
2(x + 3y) (x – 7y)
(ii) 32 – 2(x – 4)2
Solution:-
32 – 2(x – 4)2
Take out common in all terms,
2[16 – (x – 4)2]
2[42– (x – 4)2]
We know that, a2 – b2 = (a + b) (a – b)
2[(4 + x – 4) (4 – x + 4)]
2[(x) (8 – x)]
2x (8 – x)
6.
(i) 108a2 – 3(b – c)2
Solution:-
108a2 – 3(b – c)2
Take out common in all terms,
3[36a2 – (b – c)2]
3[(6a)2 – (b – c)2]
We know that, a2 – b2 = (a + b) (a – b)
3[(6a + b – c) (6a – b + c)]
(ii) πa5 – π3ab2
Solution:-
πa5 – π3ab2
Take out common in all terms,
πa(a4 – π2b2)
πa((a2)2 – (πb)2)
We know that, a2 – b2 = (a + b) (a – b)
πa(a2 + πb) (a2 – πb)
7.
(i) 50x2 – 2(x – 2)2
Solution:-
50x2 – 2(x – 2)2
Take out common in all terms,
2[25x2 – (x – 2)2]
2[(5x)2 – (x – 2)2]
We know that, a2 – b2 = (a + b) (a – b)
2[(5x + x – 2) (5x – x + 2)]
2[(6x – 2) (4x + 2)]
2(6x – 2) (4x + 2)
(ii) (x – 2)(x + 2) + 3
Solution:-
We know that, a2 – b2 = (a + b) (a – b)
(x2 – 22) + 3
X2 – 4 + 3
X2 – 1
Then,
(x + 1) (x – 1)
8.
(i) x – 2y – x2 + 4y2
Solution:-
x – 2y – x2 + 4y2
x – 2y – (x2 + (2y)2)
We know that, a2 – b2 = (a + b) (a – b)
x – 2y – [(x + 2y) (x – 2y)]
Take out common in all terms,
(x – 2y) (1 – (x + 2y))
(x – 2y) (1 – x – 2y)
(ii) 4a2 – b2 + 2a + b
Solution:-
4a2 – b2 + 2a + b
(2a)2 – b2 + 2a + b
We know that, a2 – b2 = (a + b) (a – b)
((2a + b) (2a – b)) + 1(2a + b)
Take out common in all terms,
(2a + b) (2a – b + 1)
9.
(i) a(a – 2) – b(b – 2)
Solution:-
a(a – 2) – b(b – 2)
Above question can be written as,
a2 – 2a – b2 – 2b
Rearranging the above terms, we get,
a2 – b2 – 2a – 2b
We know that, a2 – b2 = (a + b) (a – b)[(a + b)(a – b)] – 2(a – b)
Take out common in all terms,
(a – b) (a + b – 2)
(ii) a(a – 1) – b(b – 1)
Solution:-
a(a – 1) – b(b – 1)
Above question can be written as,
a2 – a – b2 + b
Rearranging the above terms, we get,
a2 – b2 – a + b
We know that, a2 – b2 = (a + b) (a – b)[(a + b) (a – b)] – 1 (a – b)
Take out common in all terms,
(a – b) (a + b – 1)
10.
(i) 9 – x2 + 2xy – y2
Solution:-
9 – x2 + 2xy – y2
9 – x2 + 2xy – y2
Above terms can be written as,
9 – x2 + xy + xy – y2
Now,
9 – x2 + xy + 3x – 3x + 3y – 3y + xy – y2
Rearranging the above terms, we get,
9 – 3x + 3y + 3x – x2 + xy + xy – 3y – y2
Take out common in all terms,
3(3 – x + y) + x(3 – x + y) + y (-3 – y + x)
3(3 – x + y) + x(3 – x + y) – y(3 – x + y)
(3 – x + y) (3 + x – y)
(ii) 9x4 – (x2 + 2x + 1)
Solution:-
9x4 – (x2 + 2x + 1)
Above terms can be written as,
(3x2)2 – (x + 1)2 … [because (a + b)2 = a2 + 2ab + b2]
We know that, a2 – b2 = (a + b) (a – b)
So, (3x2 + x + 1) (3x2 – x – 1)
11.
(i) 9x4 – x2 – 12x – 36
Solution:-
9x4 – x2 – 12x – 36
Above terms can be written as,
9x4 – (x2 + 12x + 36)
We know that, (a + b)2 = a2 + 2ab + b2
(3x2)2 – (x2 + (2 × 6 × x) + 62)
So, (3x2)2 – (x + 6)2
We know that, a2 – b2 = (a + b) (a – b)
(3x2 + x + 6) (3x2 – x – 6)
(ii) x3 – 5x2 – x + 5
Solution:-
x3 – 5x2 – x + 5
Take out common in all terms,
x2(x – 5) – 1(x – 5)
(x – 5) (x2 – 1)
(x – 5) (x2 – 12)
We know that, a2 – b2 = (a + b) (a – b)
(x – 5) (x + 1) (x – 1)
12.
(i) a4 – b4 + 2b2 – 1
Solution:-
a4 – b4 + 2b2 – 1
Above terms can be written as,
a4 – (b4 – 2b2 + 1)
We know that, (a – b)2 = a2 – 2ab + b2
a4 – ((b2)2) – (2 × b2 × 1) + 12)
(a2)2 – (b2 – 1)2
We know that, a2 – b2 = (a + b) (a – b)
(a2 + b2 – 1) (a2 – b2 + 1)
(ii) x3 – 25x
Solution:-
x3 – 25x
Take out common in all terms,
x(x2 – 25)
Above terms can be written as,
x(x2 – 52)
We know that, a2 – b2 = (a + b) (a – b)
x(x + 5) (x – 5)
13.
(i) 2x4 – 32
Solution:-
2x4 – 32
Take out common in all terms,
2(x4 – 16)
Above terms can be written as,
2((x2)2 – 42)
We know that, a2 – b2 = (a + b) (a – b)
2(x2 + 4) (x2 – 4)
2(x2 + 4) (x2 – 22)
2(x2 + 4) (x + 2) (x – 2)
(ii) a2(b + c) – (b + c)3
Solution:-
a2(b + c) – (b + c)3
Take out common in all terms,
(b + c) (a2 – (b + c)2)
We know that, a2 – b2 = (a + b) (a – b)
(b + c) (a + b + c) (a – b – c)
14.
(i) (a + b)3 – a – b
Solution:-
(a + b)3 – a – b
Above terms can be written as,
(a + b)3 – (a + b)
Take out common in all terms,
(a + b) [(a + b)2 – 1]
(a + b) [(a + b)2 – 12]
We know that, a2 – b2 = (a + b) (a – b)
(a + b) (a + b + 1) (a + b – 1)
(ii) x2 – 2xy + y2 – a2 – 2ab – b2
Solution:-
x2 – 2xy + y2 – a2 – 2ab – b2
Above terms can be written as,
(x2 – 2xy + y2) – (a2 + 2ab + b2)
We know that, (a + b)2 = a2 + 2ab + b2 and (a – b)2 = a2 – 2ab + b2
(x2 – (2 × x × y) + y2) – (a2 + (2 × a × b) + b2)
(x – y)2 – (a + b)2
We know that, a2 – b2 = (a + b) (a – b)[(x – y) + (a + b)] [(x – y) – (a + b)]
(x – y + a + b) (x – y – a – b)
15.
(i) (a2 – b2) (c2 – d2) – 4abcd
Solution:-
(a2 – b2) (c2 – d2) – 4abcd
a2(c2 – d2) – b2 (c2 – d2) – 4abcd
a2c2 – a2d2 – b2c2 + b2d2 – 4abcd
a2c2 + b2d2 – a2d2 – b2c2 – 2abcd – 2abcd
Rearranging the above terms, we get,
a2c2 + b2d2 – 2abcd – a2d2 – b2c2 – 2abcd
We know that, (a + b)2 = a2 + 2ab + b2 and (a – b)2 = a2 – 2ab + b2
(ac – bd)2 – (ad – bc)2
(ac – bd + ad – bc) (ac – bd – ad + bc)
(ii) 4x2 – y2 – 3xy + 2x – 2y
Solution:-
4x2 – y2 – 3xy + 2x – 2y
Above terms can be written as,
x2 + 3x2 – y2 – 3xy + 2x – 2y
Rearranging the above terms, we get,
(x2 – y2) + (3x2 – 3xy) + (2x – 2y)
We know that, a2 – b2 = (a + b) (a – b) and take out common terms,
(x + y) (x – y) + 3x(x – y) + 2(x – y)
(x – y) [(x + y) + 3x + 2]
(x – y) (x + y + 3x + 2)
(x – y) (4x + y + 2)
16.
(i) x2 + 1/x2 – 11
Solution:-
x2 + 1/x2 – 11
Above terms can be written as,
x2 + (1/x2) – 2 – 9
Then, (x2 + (1/x2) – 2) – 32
We know that, (a – b)2 = a2 – 2ab + b2,
(x2 – (2 × x2 × (1/x2)) + (1/x)2)
(x – 1/x)2 – 32
We know that, a2 – b2 = (a + b) (a – b)
(x – 1/x + 3) (x – 1/x – 3)
(ii) x4 + 5x2 + 9
Solution:-
x4 + 5x2 + 9
x4 + 6x2 – x2 + 9
(x4 + 6x2 + 9) – x2
((x2)2 + (2 × x2 × 3) + 32)
We know that, (a + b)2 = a2 + 2ab + b2,
((x2)2 + (2 × x2 × 3) + 32)
So, (x2 + 3)2 – x2
We know that, a2 – b2 = (a + b) (a – b)
(x2 + 3 + x) (x2 + 3 – x)
17.
(i) a4 + b4 – 7a2b2
Solution:-
a4 + b4 – 7a2b2
Above terms can be written as,
a4 + b4 + 2a2b2 – 9a2b2
We know that, (a + b)2 = a2 + 2ab + b2,[(a2)2 + (b2)2 + (2 × a2 × b2)] – (3ab)2
(a2 + b2)2 – (3ab)2
We know that, a2 – b2 = (a + b) (a – b)
(a2 + b2 + 3ab) (a2 + b2 – 3ab)
(ii) x4 – 14x2 + 1
Solution:-
x4 – 14x2 + 1
Above terms can be written as,
x4 + 2x2 + 1 – 16x2
We know that, (a + b)2 = a2 + 2ab + b2,
So, [(x2)2 + (2 × x2 × 1) + 12] – 16x2
(x2 + 1)2 – (4x)2
We know that, a2 – b2 = (a + b) (a – b)
(x2 + 1 + 4x) (x2 + 1 – 4x)
18. Express each of the following as the difference of two squares:
(i) (x2 – 5x + 7) (x2 + 5x + 7)
Solution:-
(x2 – 5x + 7) (x2 + 5x + 7)
Rearranging the above terms, we get,
((x2 + 7) – 5x) ((x2 + 7) + 5x)
As, we know that, a2 – b2 = (a + b) (a – b)
So, (x2 + 7)2 – (5x)2
(x2 + 7)2 -25x2
(ii) (x2 – 5x + 7) (x2 – 5x – 7)
Solution:-
(x2 – 5x + 7) (x2 – 5x – 7)[(x2 – 5x) + 7) ((x2 – 5x) – 7)
As, we know that, a2 – b2 = (a + b) (a – b)
(x2 – 5x)2 – 72
(x2 – 5x)2 – 49
(iii) (x2 + 5x – 7) (x2 – 5x + 7)
Solution:-
(x2 + 5x – 7) (x2 – 5x + 7)[x2 + (5x – 7)] [x2 – (5x – 7)]
As, we know that, a2 – b2 = (a + b) (a – b)
x2 – (5x – 7)2
We know that, (a – b)2 = a2 – 2ab + b2,
X2 – [(5x)2 – (2 × 5x × 7) + 72]
X2 – (25x2 – 70x + 49)
X2 – 25x2 + 70x – 49
-24x2 + 70x – 49
19. Evaluate the following by using factors:
(i) (979)2 – (21)2
(ii) (99.9)2 – (0.1)2
Solution:
(i) (979)2 – (21)2
We know that
= (979 + 21) (979 – 21)
So we get
= 1000 ×958
= 958000
(ii) (99.9)2 – (0.1)2
We know that
= (99.9 + 0.1) (99.9 – 0.1)
So we get
= 100 × 99.8
= 9980
Exercise 4.4
Factorise the following (1 to 18):
1.
(i) x2 + 5x + 6
Solution:-
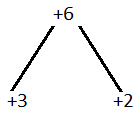 x2 + 5x + 6
x2 + 5x + 6
x2 + 3x + 2x + 6
Take out common in all terms we get,
x(x + 3) + 2 (x + 3)
(x + 3) (x + 2)
(ii) x2 – 8x + 7
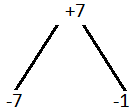 Solution:-
Solution:-
x2 – 8x + 7
x2 – 7x – x + 7
Take out common in all terms we get,
x(x – 7) – 1(x – 7)
(x – 7) (x – 1)
2.
(i) x2 + 6x – 7
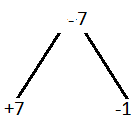 Solution:-
Solution:-
x2 + 6x – 7
x2 + 7x – x – 7
Take out common in all terms we get,
x(x + 7) – 1(x + 7)
(x + 7) (x – 1)
(ii) y2 + 7y – 18
Solution:-
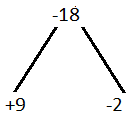 y2 + 7y – 18
y2 + 7y – 18
y2 + 9y – 2y – 18
Take out common in all terms we get,
y(y + 9) – 2(y + 9)
(y + 9) (y – 2)
3.
(i) y2 – 7y – 18
Solution:-
y2 – 7y – 18
y2 + 2y – 9y – 18
Take out common in all terms we get,
y(y + 2) – 9(y + 2)
(y + 2) (y – 9)
(ii) a2 – 3a – 54
Solution:-
a2 – 3a – 54
a2 + 6a – 9a – 54
Take out common in all terms we get,
a(a + 6) – 9(a + 6)
So, (a + 6) (a – 9)
4.
(i) 2x2 – 7x + 6
 Solution:-
Solution:-
2x2 – 7x + 6
2x2 – 4x – 3x + 6
Take out common in all terms we get,
2x(x – 2) – 3(x – 2)
(x – 2) (2x – 3)
(ii) 6x2 + 13x – 5
Solution:-
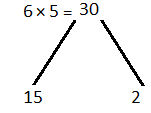 6x2 + 13x – 5
6x2 + 13x – 5
6x2 + 15x – 2x – 5
Take out common in all terms we get,
3x(2x + 5) – 1(2x + 5)
(2x + 5) (3x – 1)
5.
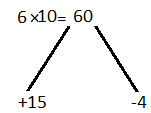 (i) 6x2 + 11x – 10
(i) 6x2 + 11x – 10
Solution:-
6x2 + 11x – 10
6x2 + 15x – 4x – 10
Take out common in all terms we get,
3x(2x + 5) – 2(2x + 5)
(2x + 5) (3x – 2)
(ii) 6x2 – 7x – 3
Solution:-
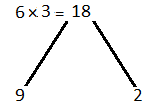 6x2 – 7x – 3
6x2 – 7x – 3
6x2 – 9x + 2x – 3
Take out common in all terms we get,
3x(2x – 3) + 1(2x – 3)
(2x – 3) (3x + 1)
6.
(i) 2x2 – x – 6
Solution:-
2x2 – x – 6
2x2 – 4x + 3x – 6
Take out common in all terms we get,
2x(x – 2) + 3(x – 2)
(x – 2) (2x + 3)
(ii) 1 – 18y – 63y2
Solution:-
1 – 18y – 63y2
1 – 21y + 3y – 63y2
Take out common in all terms we get,
1(1 – 21y) + 3y(1 – 21y)
(1 – 21y) (1 + 3y)
7.
(i) 2y2 + y – 45
Solution:-
2y2 + y – 45
2y2 + 10y – 9y – 45
Take out common in all terms we get,
2y (y + 5) – 9(y + 5)
(y + 5) (2y – 9)
(ii) 5 – 4x – 12x2
Solution:-
5 – 4x – 12x2
5 – 10x + 6x – 12x2
Take out common in all terms we get,
5(1 – 2x) + 6x(1 – 2x)
(1 – 2x) (5 + 6x)
8.
(i) x(12x + 7) – 10
Solution:-
x(12x + 7) – 10
Above terms can be written as,
12x2 + 7x – 10
12x2 + 15x – 8x – 10
Take out common in all terms we get,
3x(4x + 5) – 2(4x + 5)
(4x + 5) (3x – 2)
(ii) (4 – x)2 – 2x
Solution:-
(4 – x)2 – 2x
We know that, (a – b)2 = a2 – 2ab + b2
So, (42 – (2 × 4 × x) + x2) – 2x
16 – 8x + x2 – 2x
x2 – 10x + 16
x2 – 8x – 2x + 16
Take out common in all terms we get,
x(x – 8) – 2(x – 8)
(x – 8) (x -2)
9.
(i) 60x2 – 70x – 30
Solution:-
60x2 – 70x – 30
Take out common in all terms we get,
10(6x2 – 7x – 3)
10(6x2 – 9x + 2x – 3)
Again, take out common in all terms we get,
10(3x(2x – 3) + 1(2x – 3))
10(2x – 3) (3x + 1)
(ii) x2 – 6xy – 7y2
Solution:-
x2 – 6xy – 7y2
x2 – 7xy + xy – 7y2
Take out common in all terms we get,
x(x – 7y) + y(x – 7y)
(x – 7y) (x + y)
10.
(i) 2x2 + 13xy – 24y2
Solution:-
2x2 + 13xy – 24y2
2x2 + 16xy – 3xy – 24y2
Take out common in all terms we get,
2x(x + 8y) – 3y(x + 8y)
(x + 8y) (2x – 3y)
(ii) 6x2 – 5xy – 6y2
Solution:-
6x2 – 5xy – 6y2
6x2 – 9xy + 4xy – 6y2
Take out common in all terms we get,
3x(2x – 3y) + 2y (2x – 3y)
(2x – 3y) (3x + 2y)
11.
(i) 5x2 + 17xy – 12y2
Solution:-
5x2 + 17xy – 12y2
5x2 + 20xy – 3xy – 12y2
Take out common in all terms we get,
5x(x + 4y) – 3y(x + 4y)
(x + 4y) (5x – 3y)
(ii) x2y2 – 8xy – 48
Solution:-
x2y2 – 8xy – 48
x2y2 – 12xy + 4xy – 48
Take out common in all terms we get,
xy(xy – 12) + 4(xy – 12)
(xy – 12) (xy + 4)
12.
(i) 2a2b2 – 7ab – 30
Solution:-
2a2b2 – 7ab – 30
2a2b2 – 12ab + 5ab – 30
Take out common in all terms we get,
2ab(ab – 6) + 5 (ab – 6)
(ab – 6) (2ab + 5)
(ii) a(2a – b) – b2
Solution:-
a(2a – b) – b2
Above terms can be written as,
2a2 – ab – b2
2a2 – 2ab + ab – b2
Take out common in all terms we get,
2a(a – b) + b(a – b)
(a – b) (2a + b)
13.
(i) (x – y)2 – 6(x – y) + 5
Solution:-
(x – y)2 – 6(x – y) + 5
Above terms can be written as,
(x – y)2 – 5(x – y) – (x – y) + 5
(x – y) (x – y – 5) – 1(x – y – 5)
Then,
(x – y – 5) (x – y – 1)
(ii) (2x – y)2 – 11(2x – y) + 28
Solution:-
(2x – y)2 – 11(2x – y) + 28
Above terms can be written as,
(2x – y)2 – 7(2x – y) – 4(2x – y) + 28
(2x – y) (2x – y – 7) – 4(2x – y – 7)
(2x – y – 7) (2x – y – 4)
14.
(i) 4(a – 1)2 – 4(a – 1) – 3
Solution:-
4(a – 1)2 – 4(a – 1) – 3
Above terms can be written as,
4(a – 1)2 – 6(a – 1) + 2(a – 1) – 3
Take out common in all terms we get,
2(a – 1) [2(a – 1) – 3] + 1[2(a – 1) – 3]
(2(a – 1) – 3) (2(a – 1) + 1)
(2a – 2 – 3) (2a – 2 + 1)
(2a – 5) (2a – 1)
(ii) 1 – 2a – 2b – 3(a + b)2
Solution:-
1 – 2a – 2b – 3(a + b)2
Above terms can be written as,
1 – 2(a + b) – 3(a + b)2
1 – 3(a + b) + (a + b) – 3(a + b)2
Take out common in all terms we get,
1(1 – 3(a + b)) + (a + b) (1 – (a + b))
(1 – 3(a + b)) (1 + (a + b))
(1 – 3a + 3b) (1 + a + b)
15.
(i) 3 – 5a – 5b – 12(a + b)2
Solution:-
3 – 5a – 5b – 12(a + b)2
Above terms can be written as,
3 – 5(a + b) – 12(a + b)2
3 – 9(a + b) + 4(a + b) – 12(a + b)2
Take out common in all terms we get,
3(1 – 3(a + b)) + 4(a + b) (1 – 3(a + b))
(1 – 3(a + b)) (3 + 4(a + b))
(1 – 3a – 3b) (3 + 4a + 4b)
(ii) a4 – 11a2 + 10
Solution:-
a4 – 11a2 + 10
Above terms can be written as,
a4 – 10a2 – a2 + 10
Take out common in all terms we get,
a2 (a2 – 10) – 1(a2 – 10)
(a2 – 10) (a2 – 1)
16.
(i) (x + 4)2 – 5xy -20y – 6y2
Solution:-
(x + 4)2 – 5xy -20y – 6y2
Above terms can be written as,
(x + 4)2 – 5y(x + 4) – 6y2
(x + 4)2 – 6y(x + 4) + y(x + 4) – 6y2
Take out common in all terms we get,
(x + 4) (x + 4 – 6y) + y(x + 4 – 6y)
(x – 6y + 4) (x + 4 + y)
(ii) (x2 – 2x2) – 23(x2 – 2x) + 120
Solution:-
(x2 – 2x2) – 23(x2 – 2x) + 120
Above terms can be written as,
(x2 – 2x)2 – 15(x2 – 2x) – 8(x2 – 2x) + 120
Take out common in all terms we get,
(x2 – 2x) (x2 – 2x – 15) – 8(x2 – 2x – 15)
(x2 – 2x – 15) (x2 – 2x – 8)
17. 4(2a – 3)2 – 3(2a – 3) (a – 1) – 7 (a – 1)2
Solution:-
4(2a – 3)2 – 3(2a – 3) (a – 1) – 7 (a – 1)2
Let us assume, 2a – 3 = p and a – 1 = q
So, 4p2 – 3pq – 7q2
Then, 4p2 – 7pq + 4pq – 7q2
Take out common in all terms we get,
P(4p – 7q) + q(4p – 7q)
(4p – 7q) (p + q)
Now, substitute the value of p and q we get,
(4(2a – 3) – 7(a – 1)) (2a – 3 + a – 1)
(8a – 12 – 7a + 7) (3a – 4)
(a – 5) (3a – 4)
18. (2x2 + 5x) (2x2 + 5x – 19) + 84
Solution:-
(2x2 + 5x) (2x2 + 5x – 19) + 84
Let us assume, 2x2 + 5x = p
So, (p) (p – 19) + 84
p2 – 19p + 84
p2 – 12p – 7p + 84
p(p – 12) – 7(p – 12)
(p – 12) (p – 7)
Now, substitute the value of p we get,
(2x2 + 5x – 12) (2x2 + 5x – 7)
Exercise 4.5
Factorise the following (1 to 13):
1.
(i) 8x3 + y3
Solution:-
8x3 + y3
Above terms can be written as,
(2x)3 + y3
We know that, a3 + b3 = (a + b) (a2 – ab + b2)
Where, a = 2x, b = y
Then, (2x)3 + y3 = (2x + y) ((2x)2 – (2x × y) + y2)
= (2x + y) (4x2 – 2xy + y2)
(ii) 64x3 – 125y3
Solution:-
64x3 – 125y3
Above terms can be written as,
(4x)3 – (5y)3
We know that, a3 – b3 = (a – b) (a2 + ab + b2)
Where, a = 4x, b = 5y
Then, (4x)3 – (5y)3 = (4x – 5y) ((4x)2 + (4x × 5y) + 5y2)
= (4x – 5y) (16x2 + 2oxy + 25y2)
2.
(i) 64x3 + 1
Solution:-
64x3 + 1
Above terms can be written as,
(4x)3 + 13
We know that, a3 + b3 = (a + b) (a2 – ab + b2)
Where, a = 4x, b = 1
Then, (4x)3 + 13 = (4x + 1) ((4x)2 – (4x × 1) + 12)
= (4x + 1) (16x2 – 4x + 1)
(ii) 7a3 + 56b3
Solution:-
7a3 + 56b3
Take out common in all terms we get,
7(a3 + 8b3)
Above terms can be written as,
7(a3 + (2b)3)
We know that, a3 + b3 = (a + b) (a2 – ab + b2)
Where, a = a, b = 2b
Then, 7[(a)3 + (2b)3] = 7[(a + 2b) ((a)2 – (a × 2b) + (2b)2)]
= 7(a + 2b) (a2 – 2ab + 4b2)
3.
(i) (x6/343) + (343/x6)
Solution:-
(x6/343) + (343/x6)
Above terms can be written as,
(x2/7)3 + (7/x2)3
We know that, a3 + b3 = (a + b) (a2 – ab + b2)
Where, a = (x2/7), b = (7/x2)
Then, (x2/7)3 + (7/x2)3 = [(x2/7) + (7/x2)] [(x2/7)2 – ((x2/7) × (7/x2)) + (7/x2)2]
= [(x2/7) + (7/x2)] [(x4/49) – 1 + (49/x4)]
(ii) 8x3 – 1/27y3
Solution:-
8x3 – 1/27y3
Above terms can be written as,
(2x)3 – (1/3y)3
We know that, a3 – b3 = (a – b) (a2 + ab + b2)
Where, a = 2x, b = (1/3y)
Then, (2x)3 – (1/3y)3 = (2x – (1/3y)) ((2x)2 + (2x × (1/3y)) + (3y)2)
= (2x – (1/3y)) (4x2 + (2x/3y) + 9y2)
4.
(i) x2 + x5
Solution:-
x2 + x5
Take out common in all terms we get,
x2(1 + x3)
x2(13 + x3)
We know that, a3 + b3 = (a + b) (a2 – ab + b2)
Where, a = 1, b = x
= x2 [(1 + x) (12 – (1 × x) + x2)]
= x2 (1 + x) (1 – x + x2)
(ii) 32x4 – 500x
Solution:-
32x4 – 500x
Take out common in all terms we get,
4x(8x3 – 125)
Above terms can be written as,
4x((2x)3 – 53)
We know that, a3 – b3 = (a – b) (a2 + ab + b2)
Where, a = 2x, b = 5
= 4x(2x – 5) ((2x)2 + (2x × 5) + 52)
= 4x(2x – 5) (4x2 + 10x + 25)
5.
(i) 27x3y3 – 8
Solution:-
27x3y3 – 8
Above terms can be written as,
(3xy)3 – 23
We know that, a3 – b3 = (a – b) (a2 + ab + b2)
Where, a = 3xy, b = 2
= (3xy – 2) ((3xy)2 + (3xy × 2) + 22)
= (3xy – 2) (9x2y2 + 6xy + 4)
(ii) 27(x + y)3 + 8(2x – y)3
Solution:-
27(x + y)3 + 8(2x – y)3
Above terms can be written as,
33(x + y)3 + 23(2x – y)3
(3(x + y))3 + (2(x – y))3
We know that, a3 + b3 = (a + b) (a2 – ab + b2)
Where, a = 3(x + y), b = 2(x – y)
= [3(x + y) + 2(2x – y)] [(3(x + y))3 – (3(x + y) × 2(2x – y)) + (2(2x – y))2]
= [3x + 3y + 4x – 2y] [9(x + y)2 – 6(x + y)(2x – y) + 4(2x – y)2]
= (7x – y) [9(x2 + y2 + 2xy) – 6(2x2 – xy + 2xy – y2) + 4(4x2 + y2 – 4xy)]
= (7x – y) [9x2 + 9y2 + 18xy – 12x2 – 6xy – 6y2 + 16x2 + 4y2 – 16xy]
= (7x – y) [13x2 – 4xy + 19y2]
6.
(i) a3 + b3 + a + b
Solution:-
a3 + b3 + a + b
(a3 + b3) + (a + b)
We know that, a3 + b3 = (a + b) (a2 – ab + b2)[(a + b) (a2 – ab + b2)] + (a + b)
(a + b) (a2 – ab + b2 + 1)
(ii) a3 – b3 – a + b
Solution:-
a3 – b3 – a + b
(a3 – b3) – (a – b)
We know that, a3 – b3 = (a – b) (a2 + ab + b2)[(a – b) (a2 + ab + b2)] – (a – b)
(a – b) (a2 + ab + b2 – 1)
7.
(i) x3 + x + 2
Solution:-
x3 + x + 2
Above terms can be written as,
x3 + x + 1 + 1
Rearranging the above terms, we get
(x3 + 1) (x + 1)
(x3 + 13) (x + 1)
We know that, a3 + b3 = (a + b) (a2 – ab + b2)[(x + 1) (x2 – x + 1)] + (x + 1)
(x + 1) (x2 – x + 1 + 1)
(x + 1) (x2 – x + 2)
(ii) a3 – a – 120
Solution:-
a3 – a – 120
Above terms can be written as,
a3 – a – 125 + 5
Rearranging the above terms, we get
a3 – 125 – a + 5
(a3 – 125) – (a – 5)
(a3 – 53) – (a – 5)
We know that, a3 – b3 = (a – b) (a2 + ab + b2)[(a – 5) (a2 + 5a + 52)] – (a – 5)
(a – 5) (a2 + 5a + 25) – (a – 5)
(a – 5) (a2 + 5a + 25 – 1)
(a – 5) (a2 + 5a + 24)
8.
(i) x3 + 6x2 + 12x + 16
Solution:-
x3 + 6x2 + 12x + 16
x3 + 6x2 + 12x + 8 + 8
Above terms can be written as,
(x3 + (3 × 2 × x2) + (3 × 22 × x) + 23) + 8
We know that, (a + b)3 = a3 + b3 + 3a2b + 3ab2
Now a = x and b = 2
So, (x + 2)3 + 23
We know that, a3 + b3 = (a + b) (a2 – ab + b2)
(x + 2 + 2) ((x + 2)2 – (2 × (x + 2)) + 22)
(x + 4) (x2 + 4 + 4x – 2x – 4 + 4)
(x + 4) (x2 + 2x + 4)
(ii) a3 – 3a2b + 3ab2 – 2b3
Solution:-
a3 – 3a2b + 3ab2 – 2b3
Above terms can be written as,
a3 – 3a2b + 3ab2 – b3 – b3
We know that, (a – b)3 = a3 – b3 – 3a2b + 3ab2
So, (a – b)3 + b3
We also know that, a3 – b3 = (a – b) (a2 + ab + b2)
Where, a = a – b, b = b
(a – b – b) ((a – b)2 + (a – b)b + b2)
(a – 2b) (a2 + b2 – 2ab + ab – b2 + b2)
(a – 2b) (a2 + b2 – ab)
9.
(i) 2a3 + 16b3 – 5a – 10b
Solution:-
2a3 + 16b3 – 5a – 10b
Above terms can be written as,
2(a3 + 8b3) – 5(a + 2b)
2(a3 + (2b)3) – 5(a + 2b)
We know that, a3 + b3 = (a + b) (a2 – ab + b2)
2[(a + 2b) (a2 – 2ab + 4b2)] – 5(a + 2b)
(a + 2b) (2a2 – 4ab + 8b2 – 5)
(ii) a3 – (1/a3) – 2a + 2/a
Solution:-
a3 – (1/a3) – 2a + 2/a
(a3 – (1/a)3) – 2a + 2/a
We know that, a3 – b3 = (a – b) (a2 + ab + b2)[(a – 1/a) – (a2 + (a × 1/a) + (1/a)2] – 2(a – 1/a)
(a – 1/a) (a2 + 1 + 1/a2) – 2(a – 1/a)
(a – 1/a) (a2 + 1 + 1/a2 – 2)
(a – 1/a) (a2 + (1/a2) – 1)
10.
(i) a6 – b6
Solution:-
a6 – b6
Above terms can be written as,
(a2)3 – (b2)3
We know that, a3 – b3 = (a – b) (a2 + ab + b2)
So, a = a2, b = b2
(a2 – b2) ((a2)2) + a2b2 + (b2)2)
(a2 – b2) (a4 + a2b2 + b4)
(ii) x6 – 1
Solution:-
x6 – 1
Above terms can be written as,
(x2)3 – 13
We know that, a3 – b3 = (a – b) (a2 + ab + b2)
So, a = x2, b = 1
(x2 – 1) ((x2)2 + (x2 × 1) + 12)
(x2 – 1) (x4 + x2 + 1)
11.
(i) 64x6 – 729y6
Solution:-
64x6 – 729y6
Above terms can be written as,
(2x)6 – (3y)6[(2x)2]3 – [(3y)2]3
We know that, a3 – b3 = (a – b) (a2 + ab + b2)
So, a = (2x)2, b = (3y)2[(2x)2 – (3y)2] [((2x)2)2 + ((2x)2× (3y)2) + ((3y)2)2]
(4x2 – 9y2) [16x4 + (4x2 × 9y2) + (9y2)2]
(4x2 – 9y2) [16x4 + 36x2y2 + 81y4] [(2x)2 – (3y)2] [16x4 + 36x2y2 + 81y4]
(2x + 3y) (2x – 3y) (16x4 + 36x2y2 + 81y4)
(ii) x3 – (8/x)
Solution:-
x3 – (8/x)
Above terms can be written as,
(1/x) (x3 – 8)
(1/x) [(x)3 – (2)3]
We know that, a3 – b3 = (a – b) (a2 + ab + b2)
So, a = x, b = 2
(1/x) (x – 2) (x2 + 2x + 4)
12.
(i) 250 (a – b)3 + 2
Solution:-
250 (a – b)3 + 2
Take out common in all terms we get,
2(125(a – b)3 + 1)
2[(5(a – b))3 + 13]
We know that, a3 + b3 = (a + b) (a2 – ab + b2)
= 2[(5a – 5b + 1) ((5a – 5b)2 – (5a – 5b)1 + 12)]
= 2(5a – 5b + 1) (25a2 + 25b2 – 50ab – 5a + 5b + 1)
(ii) 32a2x3 – 8b2x3 – 4a2y3 + b2y3
Solution:-
32a2x3 – 8b2x3 – 4a2y3 + b2y3
Take out common in all terms we get,
8x3(4a2 – b2) – y3(4a2 – b2)
(4a2 – b2) (8x3 – y3)
Above terms can be written as,
((2a)2 – b2) ((2x)3 – y3)
We know that, a3 – b3 = (a – b) (a2 + ab + b2) and (a2 – b2) = (a + b) (a – b)
(2a + b) (2a – b) [(2x – y) ((2x)2 + 2xy + y2)]
(2a + b) (2a – b) (2x – y) (4x2 + 2xy + y2)
13.
(i) x9 + y9
Solution:-
x9 + y9
Above terms can be written as,
(x3)3 + (y3)3
We know that, a3 + b3 = (a + b) (a2 – ab + b2)
Where, a = x3, b = y3
(x3 + y3) ((x3)2 – x3y3 + (y3)2)
(x3 + y3) (x6 – x3y3 + y6)
Then, (x3 + y3) in the form of (a3 + b3)
(x + y)(x2 – xy + y2) (x6 – x3y3 + y6)
(ii) x6 – 7x3 – 8
Solution:-
X6 – 7x3 – 8
Above terms can be written as,
(x2)3 – 7x3 – x3 + x3 – 8
(x2)3 – 8x3 + x3 – 23
(((x2)3) – (2x)3) + (x3 – 23)
We know that, a3 – b3 = (a – b) (a2 + ab + b2)
(x2 – 2x) ((x2)2 + (x2 × 2x) + (2x)2) + (x – 2) (x2 + 2x + 22)
(x2 – 2x) (x4 + 2x3 + 4x2) + (x – 2) (x2 + 2x + 4)
x(x – 2) x2(x2 + 2x + 4) + (x – 2) (x2 + 2x + 4)
Take out common in all terms we get,
(x – 2) (x2 + 2x + 4) ((x × x2) + 1)
(x – 2) (x2 + 2x + 4) (x3 + 1)
So, above terms are in the form of a3 + b3
Therefore, (x – 2) (x2 + 2x + 4) (x + 1) (x2 – x + 1)
Chapter test
Factorise the following (1 to 12):
1.
(i) 15(2x – 3)3 – 10(2x – 3)
Solution:-
15(2x – 3)3 – 10(2x – 3)
Take out common in both terms,
Then, 5(2x – 3) [3(2x – 3)2 – 2]
(ii) a(b – c) (b + c) – d(c – b)
Solution:-
a(b – c) (b + c) – d(c – b)
Above terms can be written as,
a(b – c) (b + c) + d(b – c)
Take out common in both terms,
(b – c) [a(b + c) + d]
(b – c) (ab + ac + d)
2.
(i) 2a2x – bx + 2a2 – b
Solution:-
2a2x – bx + 2a2 – b
Rearrange the above terms we get,
2a2x + 2a – bx – b
Take out common in both terms,
2a2(x + 1) – b(x + 1)
(x + 1) (2a2 – b)
(ii) p2 – (a + 2b)p + 2ab
Solution:-
p2 – (a + 2b)p + 2ab
Above terms can be written as,
p2 – ap – 2bp + 2ab
Take out common in both terms,
p(p – a) – 2b(p – a)
(p – a) (p – 2b)
3.
(i) (x2 – y2)z + (y2 – z2)x
Solution:-
(x2 – y2)z + (y2 – z2)x
Above terms can be written as,
zx2 – zy2 + xy2 – xz2
Rearrange the above terms we get,
zx2 – xz2 + xy2 – zy2
Take out common in both terms,
zx(x – z) + y2(x – z)
(x – z) (zx + y2)
(ii) 5a4 – 5a3 + 30a2 – 30a
Solution:-
5a4 – 5a3 + 30a2 – 30a
Take out common in both terms,
5a(a3 – a2 + 6a – 6)
5a[a2(a – 1) + 6(a – 1)]
5a(a – 1) (a2 + 6)
4.
(i) b(c -d)2 + a(d – c) + 3c – 3d
Solution:-
b(c -d)2 + a(d – c) + 3c – 3d
Above terms can be written as,
b(c – d)2 – a(c – d) + 3c – 3d
b(c – d)2 – a(c – d) + 3(c – d)
Take out common in both terms,
(c – d) [b(c – d) – a + 3]
(c – d) (bc – bd – a + 3)
(ii) x3 – x2 – xy + x + y – 1
Solution:-
x3 – x2 – xy + x + y – 1
Rearrange the above terms we get,
x3 – x2 – xy + y + x – 1
Take out common in both terms,
x2(x – 1) – y(x – 1) + 1(x – 1)
(x – 1) (x2 – y + 1)
5.
(i) x(x + z) – y (y + z)
Solution:-
x(x + z) – y (y + z)
x2 + xz – y2 – yz
Rearrange the above terms we get,
x2 – y2 + xz – yz
We know that, (a2 – b2) = (a + b) (a – b)
So, (x + y) (x – y) + z(x – y)
(x – y) (x + y + z)
(ii) a12x4 – a4x12
Solution:-
a12x4 – a4x12
Take out common in both terms,
a4x4 (a8 – x8)
a4x4((a4)2 – (x4)2)
We know that, (a2 – b2) = (a + b) (a – b)
a4x4 (a4 + x4) (a4 – x4)
a4x4 (a4 + x4) ((a2)2 – (x2)2)
a4x4(a4 + x4) (a2 + x2) (a2 – x2)
a4x4 (a4 + x4) (a2 + x2) (a + x) (a – x)
6.
(i) 9x2 + 12x + 4 – 16y2
Solution:-
9x2 + 12x + 4 – 16y2
Above terms can be written as,
(3x)2 + (2 × 3x × 2) + 22 – 16y2
Then, (3x + 2)2 + (4y)2
(3x + 2 + 4y) (3x + 2 – 4y)
(ii) x4 + 3x2 + 4
Solution:-
x4 + 3x2 + 4
Above terms can be written as,
(x2)2 + 3(x2) + 4
(x2)2 + (2)2 + 4x2 – x2
(x2 + 2)2 – (x2)
We know that, (a2 – b2) = (a + b) (a – b)
(x2 + 2 + x) (x2 + 2 – x)
(x2 + x + 2) (x2 – x + 2)
7.
(i) 21x2 – 59xy + 40y2
Solution:-
21x2 – 59xy + 40y2
By multiplying the first and last term we get, 21 × 40 = 840
Then, (-35) × (-24) = 840
So, 21x2 – 35xy – 24xy + 40y2
7x(3x – 5y) – 8y(3x – 5y)
(3x – 5y) (7x – 8y)
(ii) 4x3y – 44x2y + 112xy
Solution:-
4x3y – 44x2y + 112xy
Take out common in all terms,
4xy(x2 – 11x + 28)
Then, 4xy (x2 – 7x – 4x + 28)
4xy [x(x – 7) – 4(x + 7)]
4xy (x – 7) (x – 4)
8.
(i) x2y2 – xy – 72
Solution:-
x2y2 – xy – 72
x2y2 – 9xy + 8xy – 72
Take out common in all terms,
xy(xy – 9) + 8(xy – 9)
(xy – 9) (xy + 8)
(ii) 9x3y + 41x2y2 + 20xy3
Solution:-
9x3y + 41x2y2 + 20xy3
Take out common in all terms,
xy(9x2 + 41xy + y2)
Above terms can be written as,
xy (9x2 + 36xy + 5xy + 20y2)
xy [9x(x + 4y) + 5y(x + 4y)]
xy (x + 4y) (9x + 5y)
9.
(i) (3a – 2b)2 + 3(3a – 2b) – 10
Solution:-
(3a – 2b)2 + 3(3a – 2b) – 10
Let us assume, (3a – 2b) = p
p2 + 3p – 10
p2 + 5p – 2p – 10
Take out common in all terms,
p(p + 5) – 2(p + 5)
(p + 5) (p – 2)
Now, substitute the value of p
(3a – 2b + 5) (3a – 2b – 2)
(ii) (x2 – 3x) (x2 – 3x + 7) + 10
Solution:-
(x2 – 3x) (x2 – 3x + 7) + 10
Let us assume, (x2 – 3x) = q
q (q + 7) + 10
q2 + 7q + 10
q2 + 5q + 2q + 10
q(q + 5) + 2(q + 5)
(q + 5) (q + 2)
Now, substitute the value of q
(x2 – 3x + 5) (x2 – 3x + 2)
10.
(i) (x2 – x) (4x2 – 4x – 5) – 6
Solution:-
(x2 – x) (4x2 – 4x – 5) – 6
(x2 – x) [(4x2 – 4x) – 5] – 6
(x2 – x) [4(x2 – x) – 5] – 6
Let us assume x2 – x = q
So, q[4q – 5] – 6
4q2 – 5q – 6
4q2 – 8q + 3q – 6
4q(q – 2) + 3(q – 2)
(q – 2) (4q + 3)
Now, substitute the value of q
(x2 – x – 2) (4(x2 – x) + 3)
(x2 – x – 2) (4x2 – 4x + 3)
(x2 – 2x + x – 2) (4x2 – 4x + 3)[x(x – 2) + 1(x – 2)] (4x2 – 4x + 3)
(x – 2) (x + 1) (4x2 – 4x + 3)
(ii) x4 + 9x2y2 + 81y4
Solution:-
x4 + 9x2y2 + 81y4
Above terms can be written as,
x4 + 18x2y2 + 81y4 – 9x2y2
((x2)2 + (2 × x2 × 9y2) + (9y2)2) – 9x2y2
We know that, (a + b)2 = a2 + 2ab + b2
(x2 + 9y2)2 – (3xy)2
(x2 + 9y2 + 3xy) (x2 + 9y2 – 3xy)
11.
(i) (8/27)x3 – (1/8)y3
Solution:-
(8/27)x3 – (1/8)y3
Above terms can be written as,
((2/3)x)3 – (½y)3
We know that, a3 – b3 = (a – b) (a2 + ab + b2)
((2/3)x – ½y) [(2/3)x + (2/3)x (1/2)y + ((1/2)y)2]
((2/3)x – (1/2)y) [(4/9)x2 + (xy/3) + (y2/4)]
(ii) x6 + 63x3 – 64
Solution:-
x6 + 63x3 – 64
Above terms can be written as,
x6 + 64x3 – x3 – 64
Take out common in all terms,
x3 (x3 + 64) – 1(x3 + 64)
(x3 + 64) (x3 – 1)
(x3 + 43) (x3 – 13)
We know that, a3 – b3 = (a – b) (a2 + ab + b2) and a3 + b3 = (a + b) (a2 – ab + b2)
So, (x + 4) [x2 – 4x + 42] (x – 1) [x2 + x + 12]
(x + 4) (x2 – 4x + 16) (x – 1) (x2 + x + 1)
12.
(i) x3 + x2 – (1/x2) + (1/x3)
Solution:-
x3 + x2 – (1/x2) + (1/x3)
Rearranging the above terms, we get,
x3 + (1/x3) + x2 – (1/x2)
We know that, a3 – b3 = (a – b) (a2 + ab + b2) and (a2 – b2) = (a + b) (a – b)
(x + 1/x) (x2 – 1 + 1/x2) + (x + 1/x) (x – 1/x)
(x + 1/x) [x2 – 1 + 1/x2 + x – 1/x]
(ii) (x + 1)6 – (x – 1)6
Solution:-
(x + 1)6 – (x – 1)6
Above terms can be written as,
((x + 1)3)2 – ((x – 1)3)2
We know that, (a2 – b2) = (a + b) (a – b)[(x + 1)3 + (x – 1)3] [(x + 1)3 – (x – 1)3] [(x + 1) + (x – 1)][(x + 1)2 – (x – 1) (x + 1) + (x – 1)2] [(x + 1) – (x – 1)][(x + 1)2 + (x – 1) (x + 1) + (x – 1)2]
(x + 1 + x – 1) [x2 + 2x + 1 – x2 + 1 + x2 + 1 – 2x(x + 1) – x + 1] [x2 + 2x + 1 + x2 – 1 + x2 – 2x + 1]
By simplifying we get,
2x(x2 + 3) 2(3x2 + 1)
4x(x2 + 3) (3x2 + 1)
13. Show that (97)3 + (14)3 is divisible by 111
Solution:-
From the question,
(97)3 + (14)3
We know that, a3 + b3 = (a + b) (a2 – ab + b2)
So, (97 + 14) [(97)2 – (97 × 14) + (14)2]
111 [(97)2 – (97 × 14) + (14)2]
Therefore, it is clear that the given expression is divisible by 111.
14. If a + b = 8 and ab = 15, find the value of a4 + a2b2 + b4.
Solution:-
a4 + a2b2 + b4
Above terms can be written as,
a4 + 2a2b2 + b4 – a2b2
(a2)2 + 2a2b2 + (b2)2 – (ab)2
(a2 + b2)2 – (ab)2
(a2 + b2 + ab) (a2 + b – ab)
a + b = 8, ab = 15
So, (a + b)2 = 82
a2 + 2ab + b2 = 64
a2 + 2(15) + b2 = 64
a2 + b2 + 30 = 64
By transposing,
a2 + b2 = 64 – 30
a2 + b2 = 34
Then, a4 + a2b2 + b4
= (a2 + b2 + ab) (a2 + b2 – ab)
= (34 + 15) (34 – 15)
= 49 × 19
= 931
Download PDF
ML Aggarwal Solutions for Class 9 Maths Chapter 4- Factorization
Download PDF: ML Aggarwal Solutions for Class 9 Maths Chapter 4- Factorization PDF
Chapterwise ML Aggarwal Solutions for Class 9 Maths :
- Chapter 1- Rational and Irrational Numbers
- Chapter 2- Compound Interest
- Chapter 3- Expansions
- Chapter 4- Factorization
- Chapter 5- Simultaneous Linear Equations
- Chapter 6- Problems on Simultaneous Linear Equations
- Chapter 7- Quadratic Equations
- Chapter 8- Indices
- Chapter 9- Logarithms
- Chapter 10- Triangles
- Chapter 11- Mid Point Theorem
- Chapter 12- Pythagoras Theorem
- Chapter 13- Rectilinear Figures
- Chapter 14- Theorems on Area
- Chapter 15- Circle
- Chapter 16- Mensuration
- Chapter 17- Trigonometric Ratios
- Chapter 18- Trigonometric Ratios and Standard Angles
- Chapter 19- Coordinate Geometry
- Chapter 20- Statistics
About ML Aggarwal
M. L. Aggarwal, is an Indian mechanical engineer, educator. His achievements include research in solutions of industrial problems related to fatigue design. Recipient Best Paper award, Manipal Institute of Technology, 2004. Member of TSTE.
