Class 10: Maths Chapter 8 solutions. Complete Class 10 Maths Chapter 8 Notes.
Contents
ML Aggarwal Solutions for Class 10 Maths Chapter 8- Matrices
ML Aggarwal 10th Maths Chapter 8, Class 10 Maths Chapter 8 solutions
Exercise 8.1
1. Classify the following matrices:
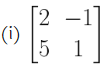
Solution:
It is square matrix of order 2

Solution:
It is row matrix of order 1 × 3
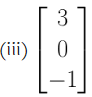
Solution:
It is column matrix of order 3 × 1
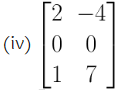
Solution:
It is a matrix of order 3 × 2

Solution:
It is a matrix of order 2 × 3

Solution:
It is zero matrix of order 2 × 3
2. (i) If a matrix has 4 elements, what are the possible order it can have?
Solution:
It can have 1 × 4, 4 × 1 or 2 × 2 order.
(ii) If a matrix has 4 elements, what are the possible orders it can have?
Solution:
It can have 1 × 8, 8 × 1, 2 × 4 or 4 × 2 order.
3. Construct a 2 × 2 matrix whose elements aij are given by
(i) aij = 2i – j
(ii) aij =i.j
Solution:
(i) Given aij = 2i – j
Therefore matrix of order 2 × 2 is

(ii) Given aij =i.j
Therefore matrix of order 2 × 2 is

4. Find the values of x and y if:
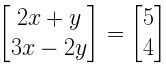
Solution:
Given
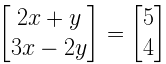
Now by comparing the corresponding elements,
2x + y = 5 ….. i
3x – 2y = 4 ….ii
Multiply (i) by 2 and (ii) by 1 we get
4x + 2y = 10 and 3x – 2y = 4
By adding we get
7x = 14
x = 14/7
x = 2
Substituting the value of x in (i)
4 + y = 5
y = 5 – 4
y = 1
Hence x = 2 and y = 1
5. Find the value of x if
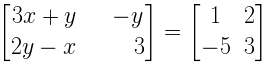
Solution:
Given
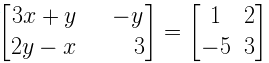
Comparing the corresponding terms of given matrix we get
-y = 2
Therefore y = -2
Again we have
3x + y = 1
3x = 1 – y
Substituting the value of y we get
3x = 1 – (-2)
3x = 1 + 2
3x = 3
x = 3/3
x = 1
Hence x = 1 and y = -2
6. If

Find the values of x and y.
Solution:
Given

Comparing the corresponding terms, we get
x + 3 = 5
x = 5 – 3
x = 2
Again we have
y – 4 = 3
y = 3 + 4
y = 7
Hence x = 2 and y = 7
7. Find the values of x, y and z if

Solution:
Given
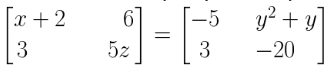
Comparing the corresponding elements of given matrix, then we get
x + 2 = -5
x = -5 – 2
x = -7
Also we have 5z = -20
z = -20/5
z = – 4
Again from given matrix we have
y2 + y – 6 = 0
The above equation can be written as
y2 + 3y – 2y – 6 = 0
y (y + 3) – 2 (y + 3) = 0
y + 3 = 0 or y – 2 = 0
y = -3 or y = 2
Hence x = -7, y = -3, 2 and z = -4
8. Find the values of x, y, a and b if
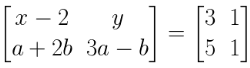
Solution:
Given
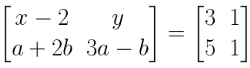
Comparing the corresponding elements
x – 2 = 3 and y = 1
x = 2 + 3
x = 5
again we have
a + 2b = 5….. i
3a – b = 1 ……ii
Multiply (i) by 1 and (ii) by 2
a + 2b = 5
6a – 2b = 2
Now by adding above equations we get
7a = 7
a = 7/7
a = 1
Substituting the value of a in (i) we get
1 + 2b = 5
2b = 5 -1
2b = 4
b = 4/2
b = 2
9. Find the values of a, b, c and d if

Solution:
Given
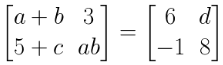
Comparing the corresponding terms, we get
3 = d
d = 3
Also we have
5 + c = -1
c = -1 – 5
c = -6
Also we have,
a + b = 6 and a b = 8
we know that,
(a – b)2 = (a + b)2 – 4 ab
(6)2 – 32 = 36 – 32 = 4 = (± 2)2
a – b = ± 2
If a – b = 2
a + b = 6
Adding the above two equations we get
2a = 4
a = 4/2
a = 2
b = 6 – 4
b = 2
Again we have a – b = -2
And a + b = 6
Adding above equations we get
2a = 4
a = 4/2
a = 2
Also, b = 6 – 2 = 4
a = 2 and b = 4
Exercise 8.2

Solution:


Solution:

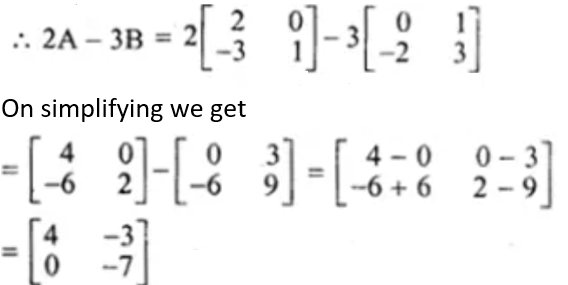
3. Simplify:
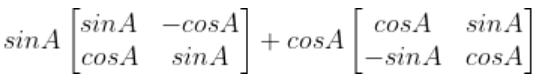
Solution:
Given,
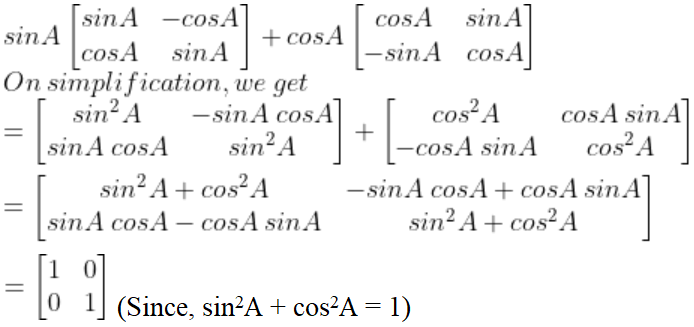
4.
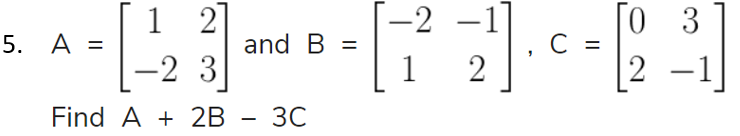
Solution:
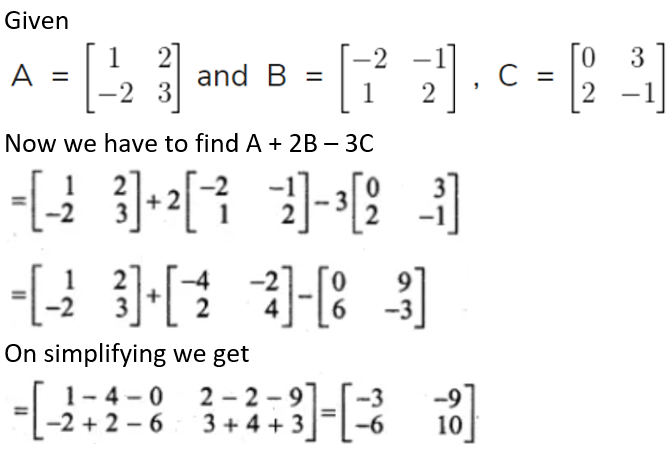
5.
Find the matrix X if:
(i) 3A + X = B
(ii) X – 3B = 2A
Solution:
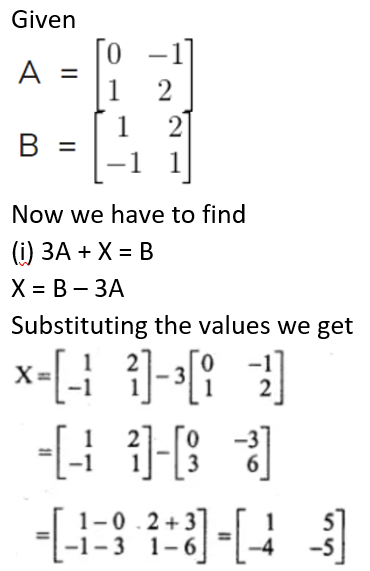
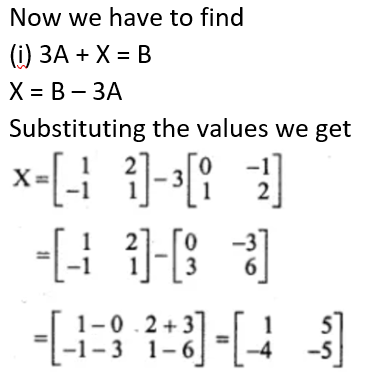
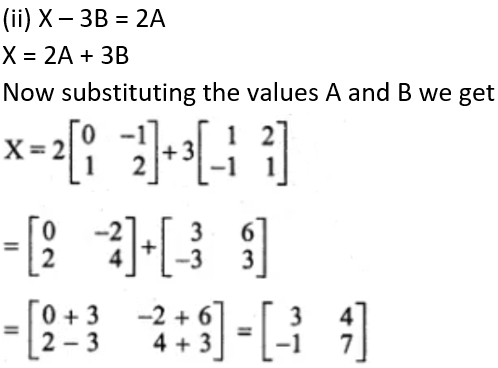
6. Solve the matrix equation
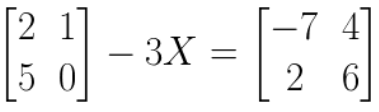
Solution:

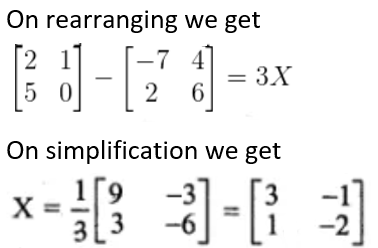
7.
Solution:

8.
Solution:

9.
Solution:


10.
Solution:
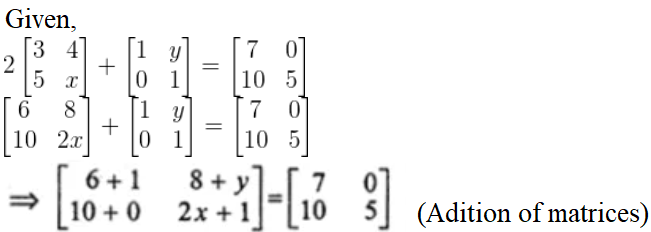
On comparing the corresponding elements, we have
8 + y = 0
Then, y = -8
And, 2x + 1 = 5
2x = 5 – 1 = 4
x = 4/2 = 2
Therefore, x = 2 and y = -8
11.
Solution:
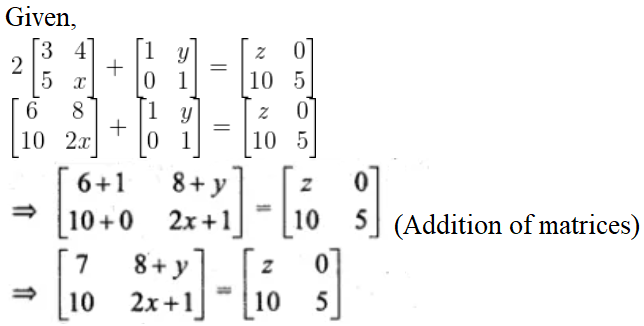
On comparing the corresponding terms, we have
2x + 1 = 5
2x = 5 -1 = 4
x = 4/2 = 2
And,
8 + y = 0
y = -8
And, z = 7
Therefore, x = 2, y = -8 and z = 7.
12.
Solution:

Now, comparing the corresponding terms, we get
4 – 4x = -8
4 + 8 = 4x
12 = 4x
x = 12/4
x = 3
And, y + 5 = 2
y = 2 – 5 =
y = -3
Therefore, x = 3 and y = -3
13.
Find the value of a, b and c.
Solution:

Next, on comparing the corresponding terms, we have
a + 1 = 5 ⇒ a = 4
b + 2 = 0 ⇒ b = -2
-c = 3 ⇒ c = -3
Therefore, the value of a, b and c are 4, -2 and -3 respectively.
14. and 5A + 2B = C, find the values of a, b and c.
Solution:
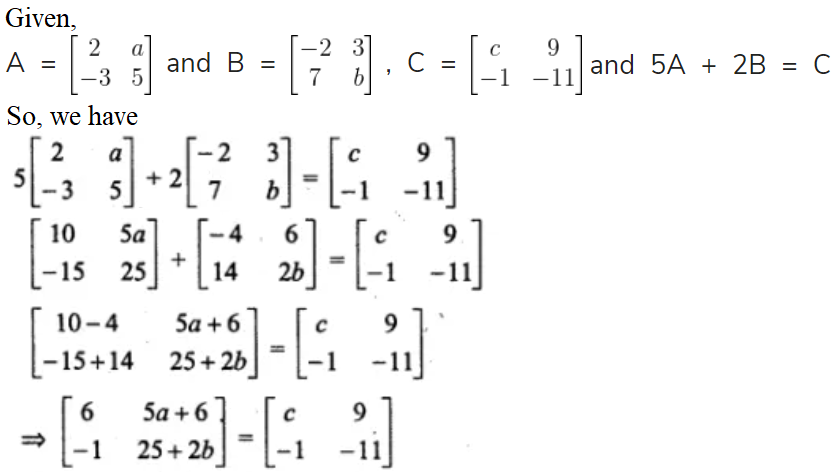
On comparing the corresponding terms, we get
5a + 6 = 9
5a = 9 – 6
5a = 3
a = 3/5
And,
25 + 2b = -11
2b = -11 – 25
2b = -36
b = -36/2
b = -18
And, c = 6
Therefore, the value of a, b and c are 3/5, -18 and 6 respectively.
Exercise 8.3

Solution:
Yes, the product is possible because of number of column in A = number of row in B
That is order of matrix is 2 × 1
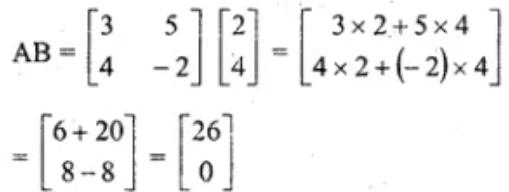
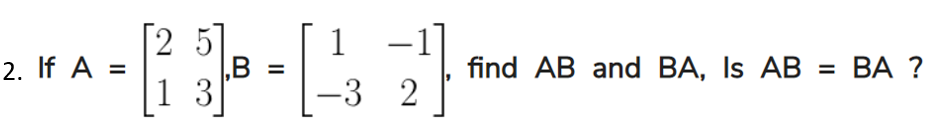
Solution:


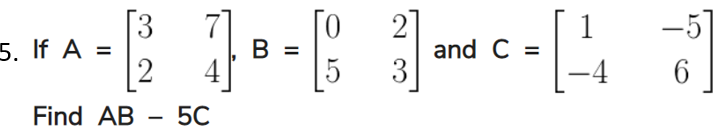
3.
Solution:

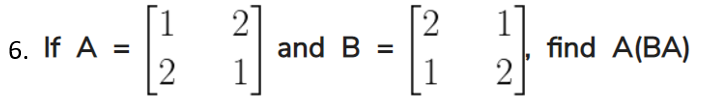
4.
Solution:

5. Given matrices:

Find the products of
(i) ABC
(ii) ACB and state whether they are equal.
Solution:
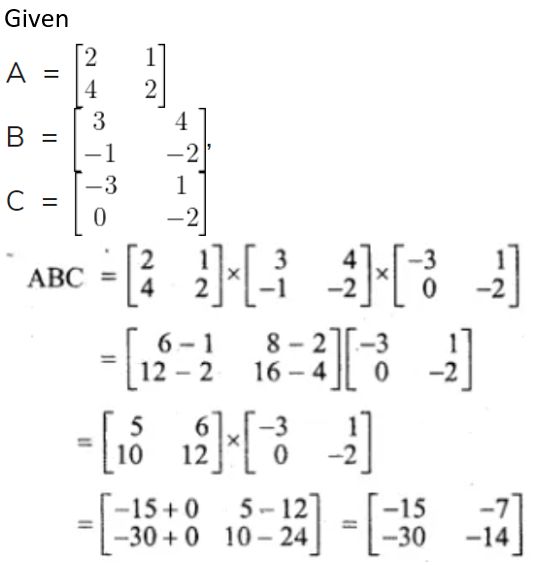
Now consider,
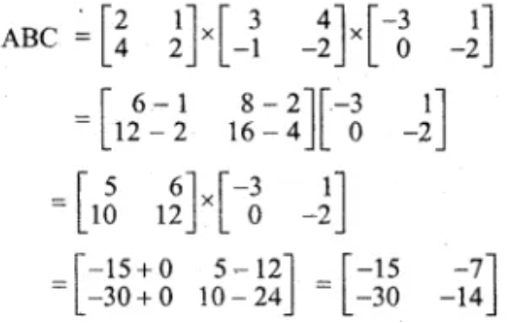
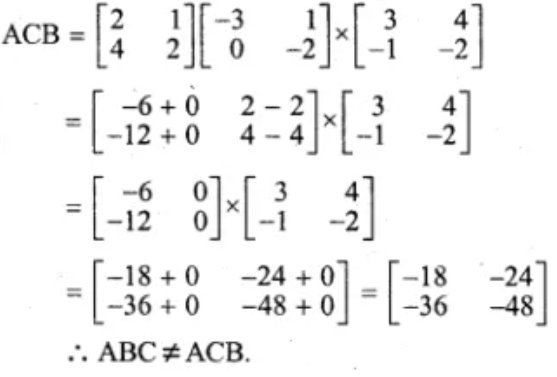
6.
Solution:
Given
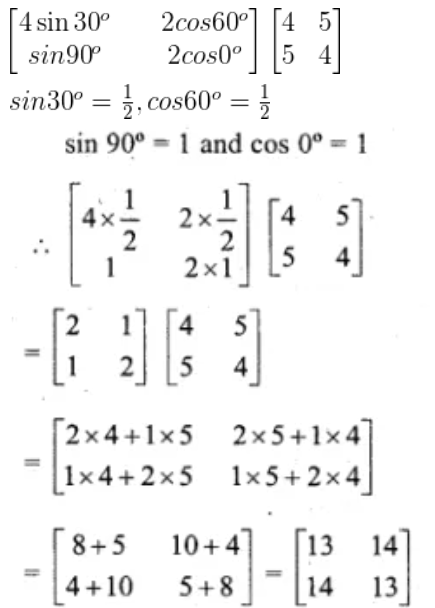
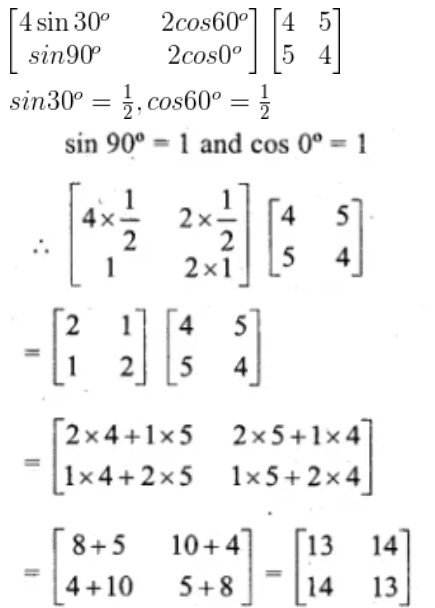
7.
Solution:
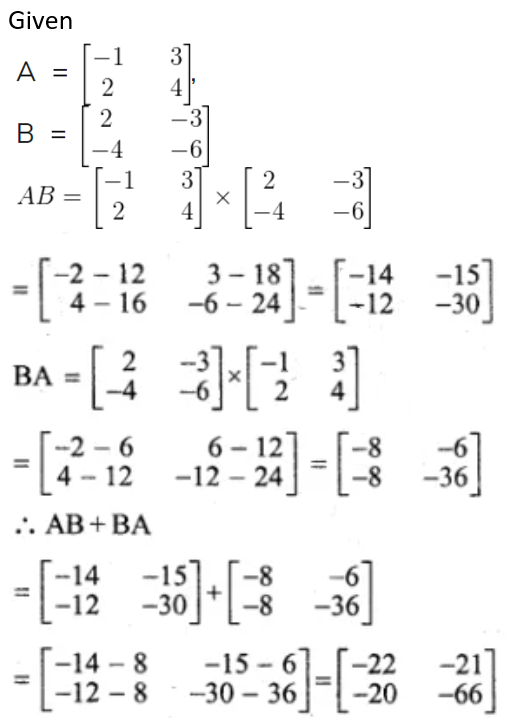

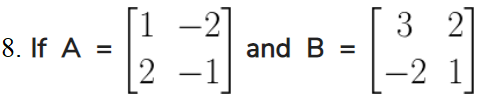
Solution:

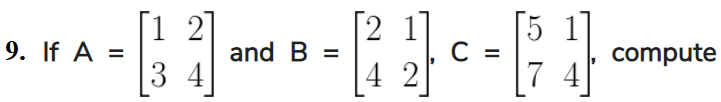
(i) A(B + C) (ii) (B + C)A
Solution:

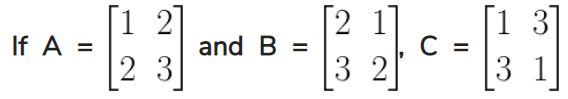
10.
Find the matrix C(B – A).
Solution:
Given,
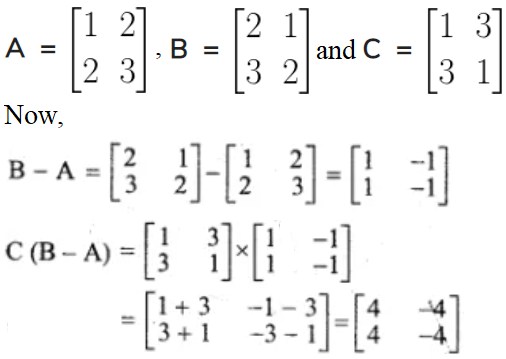
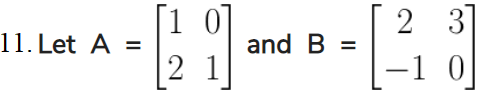
Find A2 + AB + B2.
Solution:
Given,
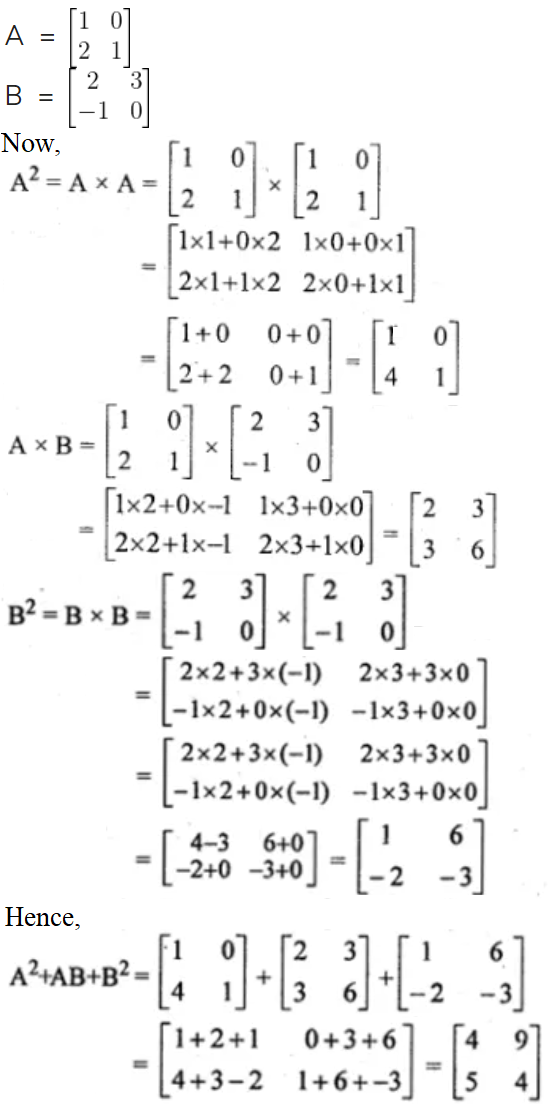

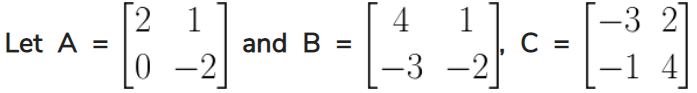
12. , find A2 + AC – 5B.
Solution:
Given,
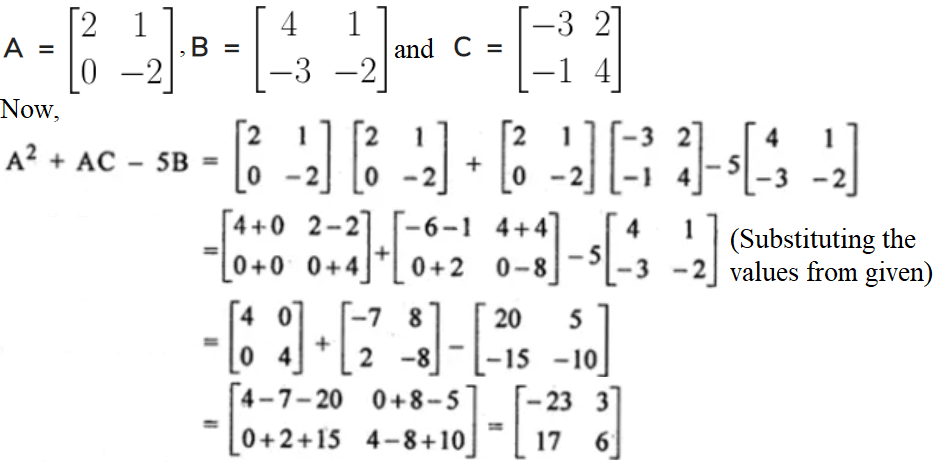

13. If , find AC + B2 – 10C.
Solution:
Given,


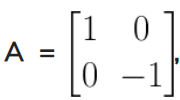
14. If find A2 and A3. Also state that which of these is equal to A.
Solution:
Given,
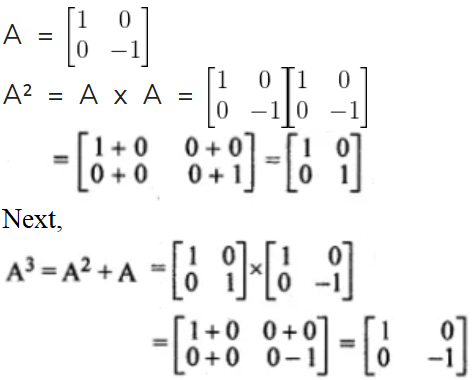
From above, its clearly seen that A3 = A.

15. If show that 6X – X2 = 9I where I is the unit matrix.
Solution:
Given,
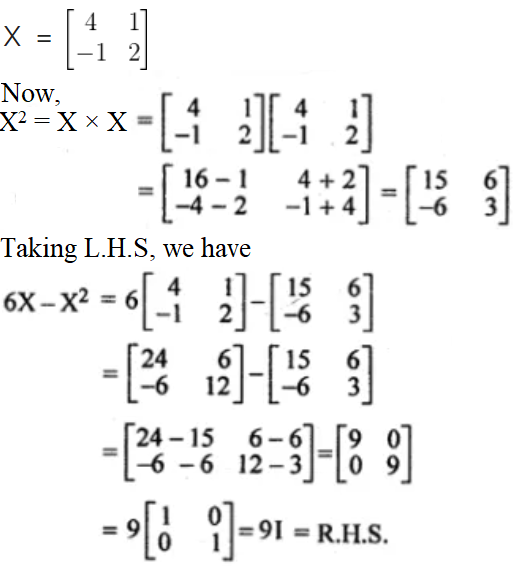
– Hence proved
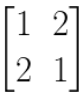
16. Show that is a solution of the matrix equation X2 – 2X – 3I = 0, where I is
the unit matrix of order 2.
Solution:
Given,

17. Find the matrix 2 × 2 which satisfies the equation

Solution:
Given,
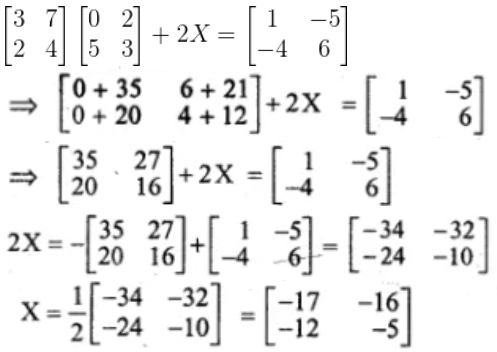

18. If find the value of x, so that A2 – 0
Solution:
Given,

On comparing,
1 + x = 0
∴ x = -1
19.

Solution:
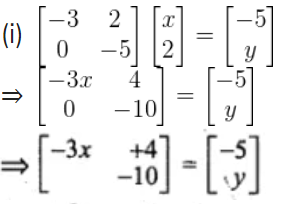
Comparing the corresponding elements,
– 3x + 4 = -5
-3x = -5 – 4 = -9
x = -9/-3 = 3
Therefore, x = 3 and y = -10.
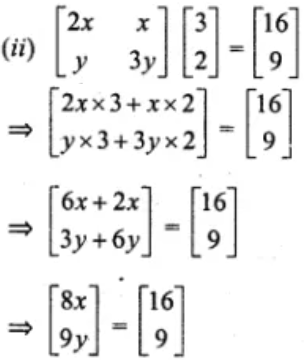
Comparing, we get
8x = 16
⇒ x = 16/8 = 2
And, 9y = 9
y = 9/9 = 1

20. Find the values of x and y if
Solution:
Given,

On comparing the corresponding elements, we have
2x + y = 3 … (i)
3x + y = 2 … (ii)
Subtracting, we get
-x = 1 ⇒ x = -1
Substituting the value of x in (i),
2(-1) + y = 3
-2 + y = 3
y = 3 + 2 = 5
Therefore, x = -1 and y = 5.
Chapter test
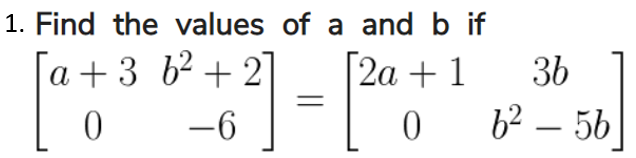
Solution:
Given

comparing the corresponding elements
a + 3 = 2a + 1
⇒ 2a – a =3 – 1
⇒ a = 2 b² + 2 = 3b
⇒ b² – 3b + 2 = 0
⇒ b² – b – 2b + 2 = 0
⇒ b (b – 1) – 2 (b – 1) = 0
⇒ (b – 1) (b – 2) = 0.
Either b – 1 = 0,
then b = 1 or b – 2 = 0,
then b = 2
Hence a = 2, b = 2 or 1
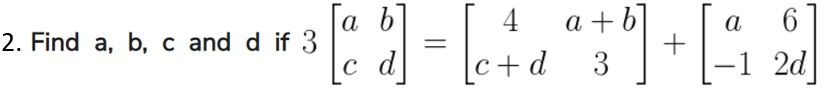
Solution:

Now comparing the corresponding elements
3a = 4 + a
a – a = 4
2a = 4
Therefore, a = 2
3b = a + b + 6
3b – b = 2 + 6
2b = 8
Therefore, b = 4
3d = 3 + 2d
3d – 2d = 3
Therefore, d = 3
3c = c + d – 1
3c – c = 3 – 1
2c = 2
Therefore, c = 1
Hence a = 2,b = 4, c = 1 and d= 3
3. Determine the matrices A and B when
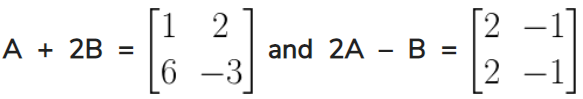
Solution:
Given,

4.
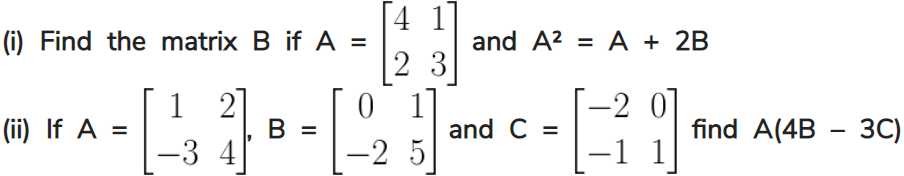
Solution:
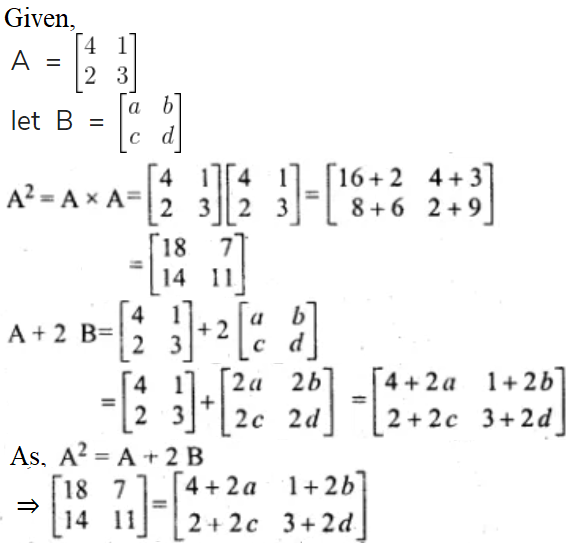
Comparing the corresponding elements, we have
4 + 2a = 18
2a = 18 – 4 = 14
a = 14/2
⇒ a = 7
1 + 2b = 7
2b = 7 – 1 = 6
b = 6/2
⇒ b = 3
2 + 2c = 14
2c = 14 – 2 = 12
2c = 12
c = 12/2
⇒ c = 6
3 + 2d = 11
2d = 11 – 3
d = 8/2
⇒ d = 4
Therefore, a = 7, b = 3, c = 6 and d = 4.
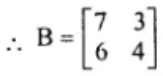
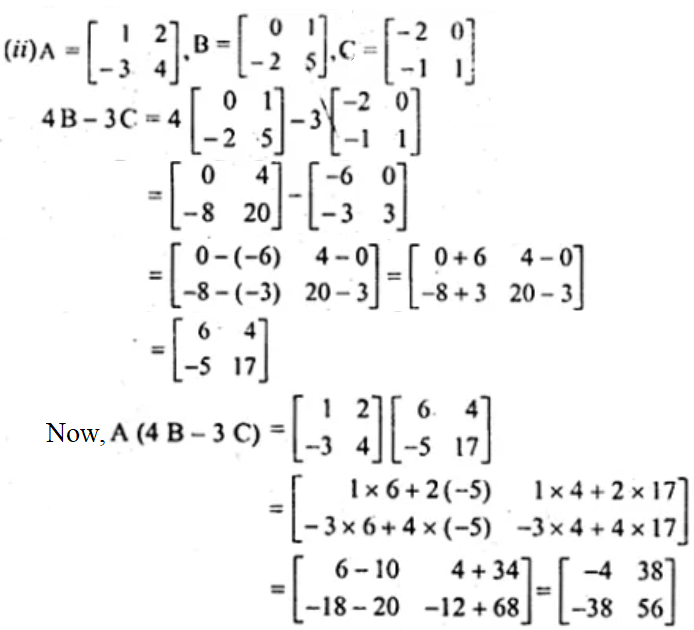
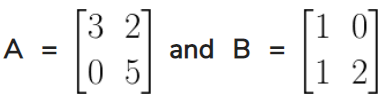
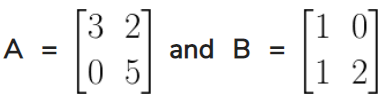
5. If , find the each of the following and state it they
are equal:
(i) (A + B) (A – B)
(ii) A2 – B2
Solution:
Given,
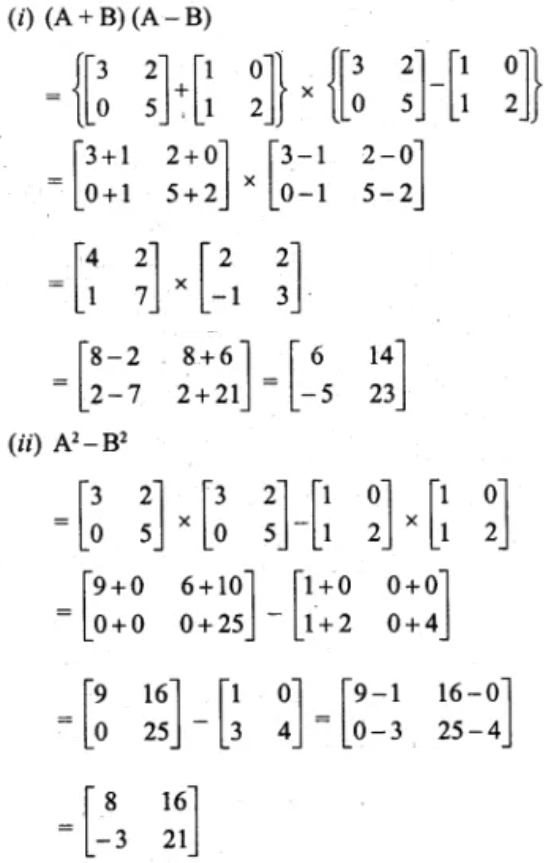
Hence, its clearly seen that (A + B) (A – B) ≠ A2 – B2.

6. If , find A2 – 5A – 14I, where I is unit matrix of order 2 × 2.
Solution:
Given,
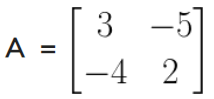
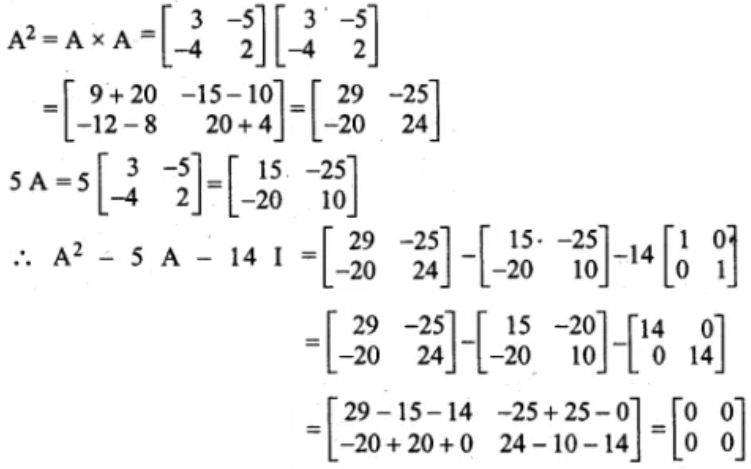
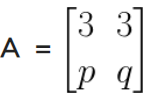
7. If and A2 = 0, find p and q.
Solution:

On comparing the corresponding elements, we have
9 + 3p = 0
3p = -9
p = -9/3
p = -3
And,
9 + 3q = 0
3q = -9
q = -9/3
q = -3
Therefore, p = -3 and q = -3.

8. If find a, b, c and d.
Solution:
Given,
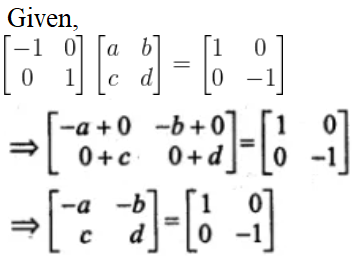
On comparing the corresponding elements, we have
-a = 1 ⇒ a = -1
-b = 0 ⇒ b = 0
c = 0 and d = -1
Therefore, a = -1, b = 0, c = 0 and = -1.
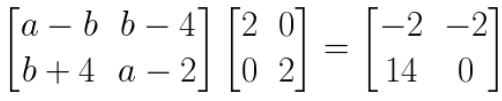
9. Find a and b if
Solution:
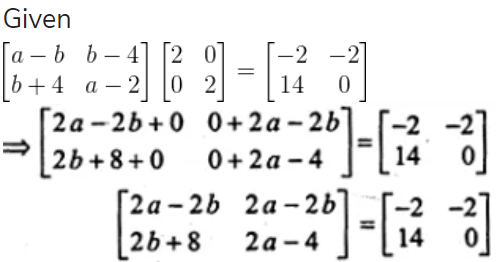
On comparing the corresponding terms, we have
2a – 4 = 0
2a = 4
a = 4/2
a = 2
And, 2a – 2b = -2
2(2) – 2b = -2
4 – 2b = -2
2b = 4 + 2
b = 6/2
b = 3
Therefore, a = 2 and b = 3.
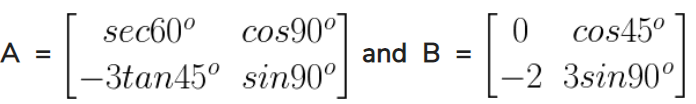
10. If
Find (i) 2A – 3B (ii) A2 (iii) BA
Solution:

Download PDF
ML Aggarwal Solutions for Class 10 Maths Chapter 8- Matrices
Download PDF: ML Aggarwal Solutions for Class 10 Maths Chapter 8- Matrices PDF
Chapterwise ML Aggarwal Solutions for Class 10 Maths :
- Chapter 1- Goods and Service Tax (GST)
- Chapter 2- Banking
- Chapter 3- Shares and Dividends
- Chapter 4- Linear Inequations
- Chapter 5- Quadratic Equations in One Variable
- Chapter 6- Factorization
- Chapter 7- Ratio and Proportion
- Chapter 8- Matrices
- Chapter 9- Arithmetic and Geometric Progression
- Chapter 10- Reflection
- Chapter 11- Section Formula
- Chapter 12- Equation of Straight Line
- Chapter 13- Similarity
- Chapter 14- Locus
- Chapter 15- Circles
- Chapter 16- Constructions
- Chapter 17- Mensuration
- Chapter 18- Trigonometric Identities
- Chapter 19- Trigonometric Tables
- Chapter 20- Heights and Distances
- Chapter 21- Measures Of Central Tendency
- Chapter 22- Probability
About ML Aggarwal
M. L. Aggarwal, is an Indian mechanical engineer, educator. His achievements include research in solutions of industrial problems related to fatigue design. Recipient Best Paper award, Manipal Institute of Technology, 2004. Member of TSTE.
