Class 10: Maths Chapter 21 solutions. Complete Class 10 Maths Chapter 21 Notes.
Contents
ML Aggarwal Solutions for Class 10 Maths Chapter 21- Measures Of Central Tendency
ML Aggarwal 10th Maths Chapter 21, Class 10 Maths Chapter 21 solutions
Exercise 21.1
1. (a) Calculate the arithmetic mean of 5.7, 6.6, 7.2, 9.3, 6.2.
(b) The weights (in kg) of 8 new born babies are 3, 3.2, 3.4, 3.5, 4, 3.6, 4.1, 3.2. Find the mean weight of the babies.
Solution:
(a) Given observations are 5.7, 6.6, 7.2, 9.3, 6.2.
Number of observations = 5
Mean = sum of observations / number of observations
Mean = (5.7+6.6+7.2+9.3+6.2)/5
= 35/5 = 7
Hence the mean of the given observations is 7.
(b) Given weight of babies are 3, 3.2, 3.4, 3.5, 4, 3.6, 4.1, 3.2
Number of observations = 8
Mean = sum of observations / number of observations
Mean = (3+3.2+3.4+3.5+4+3.6+4.1+3.2)/8
= 28/8 = 3.5 kg
Hence the mean of the weight of babies is 3.5 kg.
2.The marks obtained by 15 students in a class test are 12, 14, 07, 09, 23, 11, 08, 13, 11, 19, 16, 24, 17, 03, 20 find
(i) the mean of their marks.
(ii) the mean of their marks when the marks of each student are increased by 4.
(iii) the mean of their marks when 2 marks are deducted from the marks of each student.
(iv) the mean of their marks when the marks of each student are doubled.
Solution:
(i) Marks obtained by students are 12, 14, 07, 09, 23, 11, 08, 13, 11, 19, 16, 24, 17, 03, 20.
Number of students = 15
Mean = sum of observations / number of observations
= 12+14+07+09+23+11+08+13+11+19+16+24+17+03+20
= 207/15
= 13.8
Hence the mean of their marks is 13.8.
(ii) If mark of each student is increased by 4, total increased marks = 4×15 = 60
Total increase in sum of marks = 207+60 = 267
mean = sum of marks/number of students
mean = 267/15 = 17.8
Hence the mean is 17.8.
(iii) If mark of each student is deducted by 2, total deducted marks = 2×15 = 30
Total decrease in sum of marks = 207-30 = 177
mean = sum of marks/number of students
mean = 177/15 = 11.8
Hence the mean is 11.8.
(iv) If mark of each student is doubled , then new sum of marks = 2×207 = 414
mean = new sum of marks/number of students
mean = 414/15 = 27.6
Hence the mean is 27.6.
3. (a) The mean of the numbers 6, y, 7, x, 14 is 8. Express y in terms of x.
(b) The mean of 9 variates is 11. If eight of them are 7, 12, 9, 14, 21, 3, 8 and 15 find the 9th variate.
Solution:
(a)Given observations are 6, y, 7, x, 14.
Mean = 8
Number of observations = 5
Mean = Sum of observations/number of observations
8 = (6+y+7+x+14)/5
40 = 27+x+y
40-27 = x+y
13 = x+y
y = 13-x
Hence the answer is y = 13-x.
(b)Given mean = 11
Number of variates = 9
Variates are 7, 12, 9, 14, 21, 3, 8 ,15
Let the 9th variate be x.
Sum of variates = 7+12+9+14+21+3+8+15+x
= 89+x
Mean = Sum of variates/number of variates
11 = (89+x)/9
11×9 = 89+x
99 = 89+x
x = 99-89 = 10
Hence the 9th variate is 10.
4. (a) The mean age of 33 students of a class is 13 years. If one girl leaves the class, the mean becomes years. What is the age of the girl ?
(b) In a class test, the mean of marks scored by a class of 40 students was calculated as 18.2. Later on, it was detected that marks of one student was wrongly copied as 21 instead of 29. Find the correct mean.
Solution:
(a)Given mean age = 13
Number of students = 33
Sum of ages = mean ×number of students
= 13×33
= 429
After a girl leaves, the mean of 32 students becomes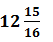 = 207/16
= 207/16
Now sum of ages = 32×207/16
= 414
So the age of the girl who left = 429-414 = 15 years.
Hence the age of the girl who left is 15 years.
(b)Mean of marks = 18.2
Number of students = 40
Total marks of 40 students = 40×18.2 = 728
Difference of marks when copied wrongly = 29-21 = 8
So total marks = 728+8 = 736
mean = 736/40
= 18.4
Hence the correct mean is 18.4.
5. Find the mean of 25 given numbers when the mean of 10 of them is 13 and the mean of the remaining numbers is 18.
Solution:
Mean of 10 numbers = 13
Sum of numbers = 13×10 = 130
Mean of remaining 15 numbers = 18
Sum of numbers = 15×18 = 270
Sum of all numbers = 130+270 = 400
Mean = sum of numbers/25 = 400/25 = 16
Hence the mean of 25 numbers is 16.
6. Find the mean of the following distribution:
| Number | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| Frequency | 1 | 2 | 5 | 6 | 3 | 2 | 1 |
Solution:
| Number (x) | Frequency (f) | fx |
| 5 | 1 | 5×1 = 5 |
| 10 | 2 | 10×2 = 20 |
| 15 | 5 | 15×5 = 75 |
| 20 | 6 | 20×6 = 120 |
| 25 | 3 | 25×3 = 75 |
| 30 | 2 | 30×2 = 60 |
| 35 | 1 | 35×1 = 35 |
| Total | Ʃf = 20 | Ʃfx = 390 |
Mean = Ʃfx/Ʃf
= 390/20 = 19.5
Hence the mean is 19.5.
7. The contents of 100 match boxes were checked to determine the number of matches they contained
| No. of matches | 35 | 36 | 37 | 38 | 39 | 40 | 41 |
| No. of boxes | 6 | 10 | 18 | 25 | 21 | 12 | 8 |
(i) Calculate, correct to one decimal place, the mean number of matches per box.
(ii) Determine how many extra matches would have to be added to the total contents of the 100 boxes to; bring the mean up to exactly 39 matches. (1997)
Solution:
(i)
| No. of matches (x) | Number of boxes (f) | fx |
| 35 | 6 | 35×6 = 210 |
| 36 | 10 | 36×10 = 360 |
| 37 | 18 | 37×18 = 666 |
| 38 | 25 | 38×25 = 950 |
| 39 | 21 | 39×21 = 819 |
| 40 | 12 | 40×12 = 480 |
| 41 | 8 | 41×8 = 328 |
| Total | Ʃf = 100 | Ʃfx = 3813 |
Mean = Ʃfx/Ʃf
= 3813/100
= 38.13
= 38.1
Hence the mean is 38.1.
(ii)New mean = 39
Ʃfx = 39×100 = 3900
So number of extra matches to be added = 3900-3813 = 87
Hence the number of extra matches to be added is 87.
8. Calculate the mean for the following distribution :
| Pocket money (in Rs) | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| No. of students | 2 | 6 | 13 | 22 | 24 | 10 | 3 |
Solution:
| Pocket money in Rs (x) | Number of students (f) | fx |
| 60 | 2 | 60×2 = 120 |
| 70 | 6 | 70×6 = 420 |
| 80 | 13 | 80×13 = 1040 |
| 90 | 22 | 90×22 = 1980 |
| 100 | 24 | 100×24 = 2400 |
| 110 | 10 | 110×10 = 1100 |
| 120 | 3 | 120×3 = 360 |
| Total | Ʃf = 80 | Ʃfx = 7420 |
Mean = Ʃfx/Ʃf
= 7420/80
= 92.75
Hence the mean is 92.75.
9. Six coins were tossed 1000 times, and at each toss the number of heads were counted and the results were recorded as under :
| No. of heads | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| No. of tosses | 20 | 25 | 160 | 283 | 338 | 140 | 34 |
Calculate the mean for this distribution.
Solution:
| No. of heads (x) | No. of tosses (f) | fx |
| 6 | 20 | 6×20 = 120 |
| 5 | 25 | 5×25 = 125 |
| 4 | 160 | 4×160 = 640 |
| 3 | 283 | 3×283 = 849 |
| 2 | 338 | 2×338 = 676 |
| 1 | 140 | 1×140 =140 |
| 0 | 34 | 0×34 = 0 |
| Total | Ʃf = 1000 | Ʃfx = 2550 |
Mean = Ʃfx/Ʃf
= 2550/1000
= 2.55
Hence the mean is 2.55.
10. Find the mean for the following distribution.
| Numbers | 60 | 61 | 62 | 63 | 64 | 65 | 66 |
| Cumulative frequency | 8 | 18 | 33 | 40 | 49 | 55 | 60 |
Solution:
| Numbers(x) | Cumulative frequency | Frequency (f) | fx |
| 60 | 8 | 8 | 60×8 = 480 |
| 61 | 18 | 18-8 = 10 | 61×10 = 610 |
| 62 | 33 | 33-18 = 15 | 62×15 = 930 |
| 63 | 40 | 40-33 = 7 | 63×7 = 441 |
| 64 | 49 | 49-40 = 9 | 64×9 = 576 |
| 65 | 55 | 55-49 = 6 | 65×6 = 390 |
| 66 | 60 | 60-55 = 5 | 66×5 = 330 |
| Total | Ʃf = 60 | Ʃfx = 3757 |
Mean = Ʃfx/Ʃf
= 3757/60
= 62.616
= 62.62
Hence the mean is 62.62.
11.
| Category | A | B | C | D | E | F | G |
| Wages (in Rs) per day | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
| No. of workers | 2 | 4 | 8 | 12 | 10 | 6 | 8 |
(i) Calculate the mean wage correct to the nearest rupee (1995)
(ii) If the number of workers in each category is doubled, what would be the new mean wage ?
Solution:
| Category | Wages in Rs. (x) | No. of workers f | fx |
| A | 50 | 2 | 100 |
| B | 60 | 4 | 240 |
| C | 70 | 8 | 560 |
| D | 80 | 12 | 960 |
| E | 90 | 10 | 900 |
| F | 100 | 6 | 600 |
| G | 110 | 8 | 880 |
| Total | Ʃf = 50 | Ʃfx = 4240 |
Mean = Ʃfx/Ʃf
= 4240/50
= 84.8
= 85
Hence the mean is 85.
(ii)If number of workers is doubled, then total number of workers = 50×2 = 100
So wages will be doubled.
Total wages = 4240×2 = 8480
Mean = Ʃfx/Ʃf
= 8480/100
= 84.8
= 85
Hence the mean is 85.
12.If the mean of the following distribution is 7.5, find the missing frequency ” f “.
| Variate | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Frequency | 20 | 17 | f | 10 | 8 | 6 | 7 | 6 |
Solution:
| Variate (x) | Frequency (f) | fx |
| 5 | 20 | 100 |
| 6 | 17 | 102 |
| 7 | f | 7f |
| 8 | 10 | 80 |
| 9 | 8 | 72 |
| 10 | 6 | 60 |
| 11 | 7 | 77 |
| 12 | 6 | 72 |
| Total | Ʃf = 74+f | Ʃfx = 563+7f |
Given mean = 7.5
Mean = Ʃfx/Ʃf
7.5= (563+f)/(74+7f)
7.5×(74+f) = 563+7f
555+7.5f = 563+7f
7.5f-7f = 563-555
0.5f = 8
f = 8/0.5 = 16
Hence the value of missing frequency f is 16.
13. Find the value of the missing variate for the following distribution whose mean is 10
| Variate (xi) | 5 | 7 | 9 | 11 | _ | 15 | 20 |
| Frequency (fi) | 4 | 4 | 4 | 7 | 3 | 2 | 1 |
Solution:
Let the missing variate be x.
| Variate (xi) | Frequency (fi) | fixi |
| 5 | 4 | 20 |
| 7 | 4 | 28 |
| 9 | 4 | 36 |
| 11 | 7 | 77 |
| x | 3 | 3x |
| 15 | 2 | 30 |
| 20 | 1 | 20 |
| Total | Ʃfi =25 | Ʃfixi = 211+3x |
Given mean = 10
Mean = Ʃfixi/Ʃfi
10= (211+3x)/25
10×25 = 211+3x
250 = 211+3x
250-211 = 3x
39 = 3x
x = 39/3 = 13
Hence the missing variate is 13.
14. Marks obtained by 40 students in a short assessment are given below, where a and b are two missing data.
| Marks | 5 | 6 | 7 | 8 | 9 |
| No. of students | 6 | a | 16 | 13 | b |
If the mean of the distribution is 7.2, find a and b.
Solution:
| Marks (x) | No. of students (f) | fx |
| 5 | 6 | 30 |
| 6 | a | 6a |
| 7 | 16 | 112 |
| 8 | 13 | 104 |
| 9 | b | 9b |
| Total | Ʃf = 35+a+b | Ʃfx = 246+6a+9b |
Given number of students = 40
Ʃf = 35+a+b = 40
a+b = 40-35 = 5
a = 5-b ……(i)
Mean = Ʃfx/Ʃf
Given mean = 7.2
( 246+6a+9b) /40 = 7.2
( 246+6a+9b) = 40×7.2
( 246+6a+9b) = 288
6a+9b = 288-246
6a+9b = 288-246
6a+9b = 42
2a+3b = 14 …..(ii)
Substitute (i) in (ii)
2(5-b)+3b = 14
10-2b+3b = 14
10+b = 14
b = 14-10 = 4
a = 5-4 = 1
Hence the value of a and b is 1 and 4 respectively.
15. Find the mean of the following distribution.
| Class interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequency | 10 | 6 | 8 | 12 | 5 |
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
| Class interval | Frequency fi | Class mark xi | fixi |
| 0-10 | 10 | 5 | 50 |
| 10-20 | 6 | 15 | 90 |
| 20-30 | 8 | 25 | 200 |
| 30-40 | 12 | 35 | 420 |
| 40-50 | 5 | 45 | 225 |
| Total | Ʃfi = 41 | Ʃfixi = 985 |
Mean = Ʃfixi/ Ʃfi
= 985/41
= 24.024
= 24.02 (approx)
Hence the mean of the distribution is 24.02.
16. Calculate the mean of the following distribution:
| Class interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Frequency | 8 | 5 | 12 | 35 | 24 | 16 |
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
| Class interval | Frequency fi | Class mark xi | fixi |
| 0-10 | 8 | 5 | 40 |
| 10-20 | 5 | 15 | 75 |
| 20-30 | 12 | 25 | 300 |
| 30-40 | 35 | 35 | 1225 |
| 40-50 | 24 | 45 | 1080 |
| 50-60 | 16 | 55 | 880 |
| Total | Ʃfi = 100 | Ʃfixi = 3600 |
Mean = Ʃfixi/ Ʃfi
= 3600/100
= 36
Hence the mean of the distribution is 36.
17. Calculate the mean of the following distribution using step deviation method:
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| No. of students | 10 | 9 | 25 | 30 | 16 | 10 |
Solution:
Class mark (xi) = (upper limit + lower limit)/2
Let assumed mean (A) = 25
Class size (h) = 10
| Class Interval | No. of students (fi) | Class mark (xi) | di = xi – A | ui = di/h | fiui |
| 0-10 | 10 | 5 | -20 | -2 | -20 |
| 10-20 | 9 | 15 | -10 | -1 | -9 |
| 20-30 | 25 | 25 | 0 | 0 | 0 |
| 30-40 | 30 | 35 | 10 | 1 | 30 |
| 40-50 | 16 | 45 | 20 | 2 | 32 |
| 50-60 | 10 | 55 | 30 | 3 | 30 |
| Total | ∑fi = 100 | ∑fiui =63 |
By step deviation method, Mean = x̄ = A+h∑fiui /∑fi
= 25+10(63/100)
= 25+10×0.63
= 25+6.3
=31.3
Hence the mean of the distribution is 31.3.
18. Find the mean of the following frequency distribution:
| Class intervals | 0-50 | 50-100 | 100-150 | 150-200 | 200-250 | 250-300 |
| frequency | 4 | 8 | 16 | 13 | 6 | 3 |
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
| Class interval | Frequency fi | Class mark xi | fixi |
| 0-50 | 4 | 25 | 100 |
| 50-100 | 8 | 75 | 600 |
| 100-150 | 16 | 125 | 2000 |
| 150-200 | 13 | 175 | 2275 |
| 200-250 | 6 | 225 | 1350 |
| 250-300 | 3 | 275 | 825 |
| Total | Ʃfi = 50 | Ʃfixi = 7150 |
Mean = Ʃfixi/ Ʃfi
= 7150/50
=143
Hence the mean of the distribution is 143.
19. The following table gives the daily wages of workers in a factory:
| Wages in Rs. | 45-50 | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 | 75-80 |
| No. of workers | 5 | 8 | 30 | 25 | 14 | 12 | 6 |
Calculate their mean by short cut method.
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
Assumed mean, A = 62.5
| Wages in Rs. | No. of workers (fi) | Class mark (xi) | di = xi – A | fidi |
| 45-50 | 5 | 47.5 | -15 | -75 |
| 50-55 | 8 | 52.5 | -10 | -80 |
| 55-60 | 30 | 57.5 | -5 | -150 |
| 60-65 | 25 | 62.5 | 0 | 0 |
| 65-70 | 14 | 67.5 | 5 | 70 |
| 70-75 | 12 | 72.5 | 10 | 120 |
| 75-80 | 6 | 77.5 | 15 | 90 |
| Total | ∑fi = 100 | ∑fidi = -25 |
By short cut method, Mean = x̄ = A+∑fidi /∑fi
= 62.5+-25/100
= 62.5-0.25
= 62.25
Hence the mean of the distribution is Rs.62.25.
20. Calculate the mean of the distribution given below using the short cut method.
| Marks | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 |
| No. of students | 2 | 6 | 10 | 12 | 9 | 7 | 4 |
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
Assumed mean, A = 45.5
| Marks | No. of students (fi) | Class mark (xi) | di = xi – A | fidi |
| 11-20 | 2 | 15.5 | -30 | -60 |
| 21-30 | 6 | 25.5 | -20 | -120 |
| 31-40 | 10 | 35.5 | -10 | -100 |
| 41-50 | 12 | 45.5 | 0 | 0 |
| 51-60 | 9 | 55.5 | 10 | 90 |
| 61-70 | 7 | 65.5 | 20 | 140 |
| 71-80 | 4 | 75.5 | 30 | 120 |
| Total | ∑fi = 50 | ∑fidi = 70 |
By short cut method, Mean = x̄ = A+∑fidi /∑fi
= 45.5+70/50
= 45.5+1.4
= 46.9
Hence the mean of the distribution is Rs.46.9.
21. A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.
| No. of days | 0-6 | 6-10 | 10-14 | 14-20 | 20-28 | 28-38 | 38-40 |
| No. of students | 11 | 10 | 7 | 4 | 4 | 3 | 1 |
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
| No. of days | Frequency fi | Class mark xi | fixi |
| 0-6 | 11 | 3 | 33 |
| 6-10 | 10 | 8 | 80 |
| 10-14 | 7 | 12 | 84 |
| 14-20 | 4 | 17 | 68 |
| 20-28 | 4 | 24 | 96 |
| 28-38 | 3 | 33 | 99 |
| 38-40 | 1 | 39 | 39 |
| Total | Ʃfi = 40 | Ʃfixi = 499 |
Mean = Ʃfixi/ Ʃfi
= 499/40
=12.475
Hence the mean number of days a student was absent is 12.475.
22. The mean of the following distribution is 23.4. Find the value of p.
| Class intervals | 0-8 | 8-16 | 16-24 | 24-32 | 32-40 | 40-48 |
| Frequency | 5 | 3 | 10 | P | 4 | 2 |
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
| Class intervals | Frequency fi | Class mark xi | fixi |
| 0-8 | 5 | 4 | 20 |
| 8-16 | 3 | 12 | 36 |
| 16-24 | 10 | 20 | 200 |
| 24-32 | P | 28 | 28P |
| 32-40 | 4 | 36 | 144 |
| 40-48 | 2 | 44 | 88 |
| Total | Ʃfi = 24+P | Ʃfixi = 488+28P |
Given mean = 23.4
Mean = Ʃfixi/ Ʃfi
23.4 = (488+28P)/(24+P)
23.4×(24+P) = 488+28P
561.6+23.4P = 488+28P
561.6-488 = 28P -23.4P
73.6 = 4.6 P
P = 73.6/4.6 = 16
Hence the value of P is 16.
23. The following distribution shows the daily pocket allowance for children of a locality. The mean pocket allowance is Rs. 18. Find the value of f.
| Daily pocket allowance in Rs. | 11-13 | 13-15 | 15-17 | 17-19 | 19-21 | 21-23 | 23-25 |
| No. of children | 3 | 6 | 9 | 13 | f | 5 | 4 |
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
| Daily pocket allowance in Rs. | No. of children fi | Class mark xi | fixi |
| 11-13 | 3 | 12 | 36 |
| 13-15 | 6 | 14 | 84 |
| 15-17 | 9 | 16 | 144 |
| 17-19 | 13 | 18 | 234 |
| 19-21 | f | 20 | 20f |
| 21-23 | 5 | 22 | 110 |
| 23-25 | 4 | 24 | 96 |
| Total | Ʃfi = 40+f | Ʃfixi = 704+20f |
Given mean = 18
Mean = Ʃfixi/ Ʃfi
18 = (704+20f)/( 40+f)
18×(40+f) = 704+20f
720 +18f = 704+20f
720-704 = 20f-18f
16 = 2f
f = 16/2 = 8
Hence the value of f is 8.
24. The mean of the following distribution is 50 and the sum of all the frequencies is 120. Find the values of p and q.
| Class intervals | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Frequency | 17 | P | 32 | q | 19 |
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
| Class intervals | Frequency fi | Class mark xi | fixi |
| 0-20 | 17 | 10 | 170 |
| 20-40 | P | 30 | 30P |
| 40-60 | 32 | 50 | 1600 |
| 60-80 | q | 70 | 70q |
| 80-100 | 19 | 90 | 1710 |
| Total | Ʃ fi = 68+P+q | Ʃfixi = 3480+30P+70q |
Given sum of all frequencies, Ʃ fi = 120
68+P+q = 120
P+q = 120-68 = 52
P+q = 52
P = 52-q …(i)
Given mean = 50
Mean = Ʃfixi / Ʃ fi
50 = (3480+30P+70q)/120
50×120 = 3480+30P+70q
6000 = 3480+30P+70q
6000- 3480 = 30P+70q
2520 = 30P+70q
252 = 3P+7q …(ii)
Substitute (i) in (ii)
252 = 3(52-q)+7q
252 = 156-3q+7q
252-156 = 4q
4q = 96
q = 96/4 = 24
P = 52-24 = 28
Hence the value of P and q is 28 and 24 respectively.
25.The mean of the following frequency distribution is 57.6 and the sum of all the frequencies is 50. Find the values of p and q.
| Class intervals | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 | 100-120 |
| Frequency | 7 | P | 12 | q | 8 | 5 |
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
| Class intervals | Frequency fi | Class mark xi | fixi |
| 0-20 | 7 | 10 | 70 |
| 20-40 | P | 30 | 30P |
| 40-60 | 12 | 50 | 600 |
| 60-80 | q | 70 | 70q |
| 80-100 | 8 | 90 | 720 |
| 100-120 | 5 | 110 | 550 |
| Total | Ʃ fi = 32+P+q | Ʃfixi = 1940+30P+70q |
Given sum of all frequencies, Ʃ fi = 50
32+P+q = 50
P+q = 50-32= 18
P+q = 18
P = 18-q …(i)
Given mean = 57.6
Mean = Ʃfixi / Ʃ fi
57.6 = (1940+30P+70q)/50
57.6 ×50 = 1940+30P+70q
2880= 1940+30P+70q
2880- 1940 = 30P+70q
940 = 30P+70q
94 = 3P+7q …(ii)
Substitute (i) in (ii)
94 = 3(18-q)+7q
94 = 54-3q+7q
94-54= 4q
40 = 4q
q = 40/4 = 10
P = 18-10 = 8
Hence the value of P and q is 8 and 10 respectively.
26. The following table gives the life time in days of 100 electricity tubes of a certain make :
| Life time in days | No. of tubes |
| Less than 50 | 8 |
| Less than 100 | 23 |
| Less than 150 | 55 |
| Less than 200 | 81 |
| Less than 250 | 93 |
| Less than 300 | 100 |
Find the mean life time of electricity tubes.
Solution:
Class mark (xi) = (upper limit + lower limit)/2
Let assumed mean (A) = 175
Class size (h) = 50
| Class Interval | No. of tubes (cf) | Class mark (xi) | di = xi – A | ui = di/h | Frequency (fi) | fiui |
| 0-50 | 8 | 25 | -150 | -3 | 8 | -24 |
| 50-100 | 23 | 75 | -100 | -2 | 15 | -30 |
| 100-150 | 55 | 125 | -50 | -1 | 32 | -32 |
| 150-200 | 81 | 175 | 0 | 0 | 26 | 0 |
| 200-250 | 93 | 225 | 50 | 1 | 12 | 12 |
| 250-300 | 100 | 275 | 100 | 2 | 7 | 14 |
| Total | ∑fi = 100 | ∑fiui =-60 |
By step deviation method, Mean = x̄ = A+h∑fiui /∑fi
= 175+50(-60/100)
= 175+50×-0.60
= 175-30
= 145
Hence the mean of the electricity tubes is 145.
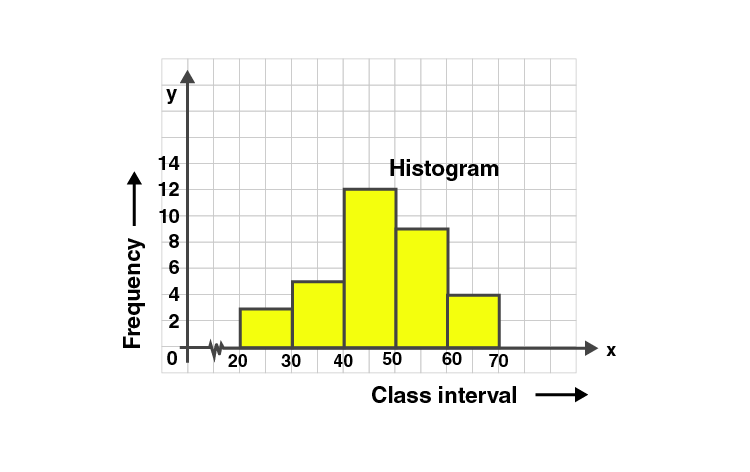
27. Using the information given in the adjoining histogram, calculate the mean correct to one decimal place.
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
Assumed mean, A = 45
| Class interval | frequency (fi) | Class mark (xi) | di = xi – A | fidi |
| 20-30 | 3 | 25 | -20 | -60 |
| 30-40 | 5 | 35 | -10 | -50 |
| 40-50 | 12 | 45 | 0 | 0 |
| 50-60 | 9 | 55 | 10 | 90 |
| 60-70 | 4 | 65 | 20 | 80 |
| ∑fi = 33 | ∑fidi = 60 |
By short cut method, Mean = x̄ = A+∑fidi /∑fi
= 45+60/33
= 45+1.81
= 46.81
= 46.8 [corrected to one decimal place]
Hence the mean is Rs.46.8.
Exercise 21.2
1. A student scored the following marks in 11 questions of a question paper : 3, 4, 7, 2, 5, 6, 1, 8, 2, 5, 7 Find the median marks.
Solution:
Arranging the data in the ascending order
1,2,2,3,4,5,5,6,7,7,8
Here number of terms, n = 11
Here n is odd.
So median = [(n+1)/2 ]th observation
= (11+1)/2
= 12/2
= 6th observation
Here 6th observation is 5.
Hence the median is 5.
2. (a) Find the median of the following set of numbers : 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7 (1990)
(b)For the following set of numbers, find the median: 10, 75, 3, 81, 17, 27, 4, 48, 12, 47, 9, 15.
Solution:
(a) Arranging the numbers in ascending order :
0, 1, 2, 2, 3, 4, 5, 5, 5, 7, 8, 9
Here, n = 12 which is even
Median = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (12/2 th term + ((12/2)+1)th term)
= ½ (6 th term + (6+1)th term)
= ½ (6 th term + 7th term)
= ½ (4+5)
= 9/2
= 4.5
Hence the median is 4.5.
(b) Arranging the numbers in ascending order :
3, 4, 9, 10, 12, 15, 17, 27, 47, 48, 75, 81
Here, n = 12 which is even
Median = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (12/2 th term + ((12/2)+1)th term)
= ½ (6 th term + (6+1)th term)
= ½ (6 th term + 7th term)
= ½ (15+17)
= ½ ×32
= 16
Hence the median is 16.
3. Calculate the mean and the median of the numbers : 2, 1, 0, 3, 1, 2, 3, 4, 3, 5
Solution:
Arranging the numbers in ascending order :
0, 1, 1, 2, 2, 3, 3, 3, 4, 5
Here, n = 10 which is even
Median = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (10/2 th term + ((10/2)+1)th term)
= ½ (5 th term + (5+1)th term)
= ½ (5 th term + 6th term)
= ½ (2+3)
= ½ ×5
= 2.5
Hence the median is 2.5.
Mean = sum of the observations/ number of observations
= Ʃxi/n
= (0+1+1+2+2+3+3+3+4+5)/10
= 24/10
= 2.4
Hence the mean is 2.4.
4.The median of the observations 11, 12, 14, (x – 2), (x + 4), (x + 9), 32, 38, 47 arranged in ascending order is 24. Find the value of x and hence find the mean.
Solution:
Observation are as follows :
11, 12, 14, (x-2), (x+4), (x+9), 32, 38, 47
n = 9
Here n is odd. So median = ((n+1)/2)th term
= (9+1)/2 )th term
= 5th term
= x+4
Given median = 24
x+4 = 24
x = 24 -4 = 20
Sum of observations = 11+12+14+(x-2)+(x+4)+(x+9)+32+38+47
= 165+3x
Substitute x = 20
Sum of observations = 165+3×20
= 165+60
= 225
Mean = Sum of observations /number of observations
= 225/9 = 25
Hence the value of x is 20 and mean is 25.
5.The mean of the numbers 1, 7, 5, 3, 4, 4, is m. The numbers 3, 2, 4, 2, 3, 3, p have mean m-1 and median q. Find
(i) p
(ii) q
(iii) the mean of p and q.
Solution:
(i) Mean of 1, 7, 5, 3, 4, 4 is m.
Here n = 6
Mean, m = (1+7+5+3+4+4)/6
m = 24/6
m = 4
Given the numbers 3, 2, 4, 2, 3, 3, p have mean m-1.
So m-1 = (3+2+4+2+3+3+p)/7
4-1 = (17+p)/7
3 = (17+p)/7
3×7 = 17+p
21 = 17+p
p = 21-17
p = 4
Hence the value of p is 4.
(ii) Given the numbers have median q.
Arranging them in ascending order
2, 2, 3, 3, 3, 4, 4
Here n = 7 which is odd
So median = ((n+1)/2)th term
q = ((7+1)/2 )th term
q = (8/2 )th term
q = 4th term
q = 3
So value of q is 3.
(iii)mean of p and q = (p+q)/2
= (4+3)/2
= 7/2
= 3.5
Hence the mean of p and q is 3.5.
6. Find the median for the following distribution:
| Wages per day in Rs. | 38 | 45 | 48 | 55 | 62 | 65 |
| No. of workers | 14 | 8 | 7 | 10 | 6 | 2 |
Solution:
We write the distribution in cumulative frequency table.
| Wages per day in Rs. | No. of workers (f) | Cumulative frequency |
| 38 | 14 | 14 |
| 45 | 8 | 22 |
| 48 | 7 | 29 |
| 55 | 10 | 39 |
| 62 | 6 | 45 |
| 65 | 2 | 47 |
Here total number of observations, n = 47 which is odd.
So median =(( n+1)/2)th term
= ((47+1)/2 )th term
= (48/2 )th term
= 24th term
= 48 [Since 23rd to 29th observation is 48]
Hence the median is 48.
7. Find the median for the following distribution.
| Marks | 35 | 45 | 50 | 64 | 70 | 72 |
| No. of students | 3 | 5 | 8 | 10 | 5 | 5 |
Solution:
We write the distribution in cumulative frequency table.
| Marks | No. of students (f) | Cumulative frequency |
| 35 | 3 | 3 |
| 45 | 5 | 8 |
| 50 | 8 | 16 |
| 64 | 10 | 26 |
| 70 | 5 | 31 |
| 72 | 5 | 36 |
Here total number of observations, n = 36 which is even.
Median = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (36/2 th term + ((36/2)+1)th term)
= ½ (18 th term + (18+1)th term)
= ½ (18 th term + 19th term)
= ½ (64+64) [Since 17th to 26th observation is 64]
= ½ ×128
= 64
Hence the median is 64.
8.Marks obtained by 70 students are given below :
| Marks | 20 | 70 | 50 | 60 | 75 | 90 | 40 |
| No. of students | 8 | 12 | 18 | 6 | 9 | 5 | 12 |
Calculate the median marks.
Solution:
We write the marks in ascending order in cumulative frequency table.
| Marks | No. of students (f) | Cumulative frequency |
| 20 | 8 | 8 |
| 40 | 12 | 20 |
| 50 | 18 | 38 |
| 60 | 6 | 44 |
| 70 | 12 | 56 |
| 75 | 9 | 65 |
| 90 | 5 | 70 |
Here total number of observations, n = 70 which is even.
Median = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (70/2 th term + ((70/2)+1)th term)
= ½ (35 th term + (35+1)th term)
= ½ (35 th term + 36th term)
= ½ (50+50) [Since all observations from 21st to 38th are 50]
= ½ ×100
= 50
Hence the median is 50.
9. Calculate the mean and the median for the following distribution :
| Number | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| Frequency | 1 | 2 | 5 | 6 | 3 | 2 | 1 |
Solution:
We write the numbers in cumulative frequency table.
| Marks (x) | No. of students (f) | Cumulative frequency | fx |
| 5 | 1 | 1 | 5 |
| 10 | 2 | 3 | 20 |
| 15 | 5 | 8 | 75 |
| 20 | 6 | 14 | 120 |
| 25 | 3 | 17 | 75 |
| 30 | 2 | 19 | 60 |
| 35 | 1 | 20 | 35 |
| Total | Ʃf = 20 | Ʃfx = 390 |
Mean = Ʃfx/Ʃf
= 390/20
= 19.5
Hence the mean is 19.5.
Here number of observations, n = 20 which is even.
So median = = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (20/2 th term + ((20/2)+1)th term)
= ½ (10 th term + (10+1)th term)
= ½ (10 th term + 11th term)
= ½ (20+20) [Since all observations from 9th to 14th are 20]
= ½ ×140
= 20
Hence the median is 20.
10. The daily wages in (rupees of) 19 workers are
41, 21, 38, 27, 31, 45, 23, 26, 29, 30, 28, 25, 35, 42, 47, 53, 29, 31, 35.
find :
(i) the median
(ii) lower quartile
(iii) upper quartile
(iv) inter quartile range
Solution:
Arranging the observations in ascending order
21, 23, 25, 26, 27, 28, 29, 29, 30, 31, 31, 35, 35, 38, 41, 42, 45, 47, 53
Here n = 19 which is odd.
(i)Median = ((n+1)/2)th term
= (19+1)/2
= 20/2
= 10th term
= 31
Hence the median is 31.
(ii) Lower quartile, Q1 = ((n+1)/4) th term
= (19+1)/4
= 20/4
= 5 th term
= 27
Hence the lower quartile is 27.
(iii)Upper quartile, Q3 = (3(n+1)/4) th term
= (3×(19+1)/4) th term
= (3×(20/4)) th term
= (3×5) th term
= 15 th term
= 41
Hence the upper quartile is 41.
(iv)Interquartile range = Q3-Q1
= 41-27
= 14
Hence the Interquartile range is 14.
11.From the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile
(iv) inter quartile range
| Variate | 15 | 18 | 20 | 22 | 25 | 27 | 30 |
| Frequency | 4 | 6 | 8 | 9 | 7 | 8 | 6 |
Solution:
We write the variates in cumulative frequency table.
| Variate | Frequency (f) | Cumulative frequency |
| 15 | 4 | 4 |
| 18 | 6 | 10 |
| 20 | 8 | 18 |
| 22 | 9 | 27 |
| 25 | 7 | 34 |
| 27 | 8 | 42 |
| 30 | 6 | 48 |
(i) Here number of observations, n = 48 which is even.
So median = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (48/2 th term + ((48/2)+1)th term)
= ½ (24 th term + (24+1)th term)
= ½ (24 th term + 25th term)
= ½ (22+22) [Since all observations from 19th to 27th are 22]
= ½ ×44
= 22
Hence the median is 22.
(ii) Lower quartile, Q1 = (n/4) th term
= (48)/4
= 12 th term
= 20
Hence the lower quartile is 20.
(iii)Upper quartile, Q3 = (3n/4) th term
= (3×48/4) th term
= (3×12)th term
= 36 th term
= 27
Hence the upper quartile is 27.
(iv)Interquartile range = Q3-Q1
= 27-20
= 7
Hence the Interquartile range is 7.
12. For the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile
| Variate | 25 | 31 | 34 | 40 | 45 | 48 | 50 | 60 |
| Frequency | 3 | 8 | 10 | 15 | 10 | 9 | 6 | 2 |
Solution:
We write the variates in cumulative frequency table.
| Variate | Frequency (f) | Cumulative frequency |
| 25 | 3 | 3 |
| 31 | 8 | 11 |
| 34 | 10 | 21 |
| 40 | 15 | 36 |
| 45 | 10 | 46 |
| 48 | 9 | 55 |
| 50 | 6 | 61 |
| 60 | 2 | 63 |
(i) Here number of observations, n = 63 which is odd.
Median = ((n+1)/2)th term
= (63+1)/2
= 64/2
= 32th term
= 40
Hence the median is 40.
(ii) Lower quartile, Q1 = ((n+1)/4) th term
= (63+1)/4
= 64/4
= 16 th term
= 34
Hence the lower quartile is 34.
(iii)Upper quartile, Q3 = (3(n+1)/4) th term
= (3×(63+1)/4) th term
= (3×(64/4)) th term
= (3×16) th term
= 48 th term
= 48
Hence the upper quartile is 48.
Exercise 21.3
1.Find the mode of the following sets of numbers ;
(i) 3, 2, 0, 1, 2, 3, 5, 3
(ii) 5, 7, 6, 8, 9, 0, 6, 8, 1, 8
(iii) 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7
Solution:
Mode is the number which appears most often in a set of numbers.
(i)Given set is 3, 2, 0, 1, 2, 3, 5, 3.
In this set, 3 occurs maximum number of times.
Hence the mode is 3.
(ii) Given set is 5, 7, 6, 8, 9, 0, 6, 8, 1, 8.
In this set, 8 occurs maximum number of times.
Hence the mode is 8.
(iii) Given set is 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7.
In this set, 5 occurs maximum number of times.
Hence the mode is 5.
2. Calculate the mean, the median and the mode of the numbers : 3, 2, 6, 3, 3, 1, 1, 2
Solution:
We arrange given data in ascending order 1, 1, 2, 2, 3, 3, 3, 6
Mean = Ʃxi/n
= (1+1+2+2+3+3+3+6)/8
= 21/8
= 2.625
Hence the mean is 2.625.
Here number of observations, n = 8 which is even.
So median = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (8/2 th term + ((8/2)+1)th term)
= ½ (4 th term + (4+1)th term)
= ½ (4 th term + 5th term)
= ½ (2+3)
= ½ ×5
= 2.5
Hence the median is 2.5.
In the given set, 3 occurs maximum number of times.
Hence the mode is 3.
3. Find the mean, median and mode of the following distribution : 8, 10, 7, 6, 10, 11, 6, 13, 10
Solution:
We arrange given data in ascending order 6, 6, 7, 8, 10, 10, 10, 11, 13
Mean = Ʃxi/n
= (6+6+7+8+10+10+10+11+13)/9
= 81/9
= 9
Hence the mean is 9.
Here number of observations, n = 9 which is odd.
Median = ((n+1)/2)th term
= (9+1)/2
= 10/2
= 5th term
= 10
Hence the median is 10.
In the given set, 10 occurs maximum number of times.
Hence the mode is 10.
4. Calculate the mean, the median and the mode of the following numbers : 3, 1, 5, 6, 3, 4, 5, 3, 7, 2
Solution:
We arrange given data in ascending order 1, 2, 3, 3, 3, 4, 5, 5, 6, 7
Mean = Ʃxi/n
= (1+2+3+3+3+4+5+5+6+7)/10
= 39/10
= 3.9
Here number of observations, n = 10 which is even.
So median = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (10/2 th term + ((10/2)+1)th term)
= ½ (5 th term + (5+1)th term)
= ½ (5 th term + 6th term)
= ½ (3+4)
= ½ ×7
= 3.5
Hence the median is 3.5.
In the given set, 3 occurs maximum number of times.
Hence the mode is 3.
5. The marks of 10 students of a class in an examination arranged in ascending order are as follows: 13, 35, 43, 46, x, x +4, 55, 61,71, 80
If the median marks is 48, find the value of x. Hence, find the mode of the given data. (2017)
Solution:
Given data in ascending order: 13, 35, 43, 46, x, x +4, 55, 61,71, 80
Given median = 48
Number of observations, n = 10 which is even.
median = ½ ( n/2 th term + ((n/2)+1)th term)
48 = ½ (10/2 th term + ((10/2)+1)th term)
48 = ½ (5 th term + (5+1)th term)
48 = ½ (5 th term + 6th term)
48 = ½ (x+x+4)
48 = ½ ×(2x+4)
48 =x+2
x = 48-2 = 46
x+4 = 46+4 = 50
So the distribution becomes
13, 35, 43, 46, 46, 50, 55, 61,71, 80
Here 46 occurs maximum number of times.
Hence the mode is 46.
6.A boy scored the following marks in various class tests during a term each test being marked out of 20: 15, 17, 16, 7, 10, 12, 14, 16, 19, 12, 16
(i) What are his modal marks ?
(ii) What are his median marks ?
(iii) What are his mean marks ?
Solution:
(i)We arrange given marks in ascending order
7, 10, 12, 12, 14, 15, 16, 16, 16, 17, 19
16 appears maximum number of times.
Hence his modal mark is 16.
(ii)Here number of observations, n = 11 which is odd.
So Median = ((n+1)/2)th term
= (11+1)/2
= 12/2
= 6th term
= 15
Hence the median is 15.
(iii) Mean = Ʃxi/n
= 7+ 10+12+12+14+ 15+16+16+16+ 17+ 19
= 154/11
= 14
Hence the mean is 14.
7. Find the mean, median and mode of the following marks obtained by 16 students in a class test marked out of 10 marks : 0, 0, 2, 2, 3, 3, 3, 4, 5, 5, 5, 5, 6, 6, 7, 8
Solution:
Given data is 0, 0, 2, 2, 3, 3, 3, 4, 5, 5, 5, 5, 6, 6, 7, 8
Number of observations, n = 16
Mean = Ʃxi/n
= (0+0+2+2+3+3+3+4+5+5+5+5+6+6+7+8)/16
= 64/16
= 4
Hence the mean is 4.
Here n = 16 which is even.
So median = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (16/2 th term + ((16/2)+1)th term)
= ½ (8 th term + (8+1)th term)
= ½ (8 th term + 9th term)
= ½ (4+5)
= 9/2
= 4.5
Hence the median is 4.5.
Here 5 appears maximum number of times.
Hence mode is 5.
8. Find the mode and median of the following frequency distribution :
| x | 10 | 11 | 12 | 13 | 14 | 15 |
| f | 1 | 4 | 7 | 5 | 9 | 3 |
Solution:
We write the data in cumulative frequency table.
| x | Frequency (f) | Cumulative frequency |
| 10 | 1 | 1 |
| 11 | 4 | 5 |
| 12 | 7 | 12 |
| 13 | 5 | 17 |
| 14 | 9 | 26 |
| 15 | 3 | 29 |
Here number of observations, n = 29 which is odd.
Median = ((n+1)/2)th term
= (29+1)/2
= 30/2
= 15th term
= 13
Hence the median is 13.
Here the frequency corresponding to 14 is maximum.
Hence the mode is 14.
9. The marks obtained by 30 students in a class assessment of 5 marks is given below:
| Marks | 0 | 1 | 2 | 3 | 4 | 5 |
| No. of students | 1 | 3 | 6 | 10 | 5 | 5 |
Calculate the mean, median and mode of the above distribution.
Solution:
We write the data in cumulative frequency table.
| Marks x | Frequency (f) | Cumulative frequency | fx |
| 0 | 1 | 1 | 0 |
| 1 | 3 | 4 | 3 |
| 2 | 6 | 10 | 12 |
| 3 | 10 | 20 | 30 |
| 4 | 5 | 25 | 20 |
| 5 | 5 | 30 | 25 |
| Total | Ʃf = 30 | Ʃfx = 90 |
Mean = Ʃfx/Ʃf
= 90/30
= 3
Hence the mean is 3.
Here number of observations, n = 30 which is even.
So median = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (30/2 th term + ((30/2)+1)th term)
= ½ (15 th term + (15+1)th term)
= ½ (15 th term + 16th term)
= ½ (3+3)
= 6/2
= 3
Hence the median is 3.
Here the mark 3 occurs maximum number of times.
Hence the mode is 3.
10. The distribution given below shows the marks obtained by 25 students in an aptitude test. Find the mean, median and mode of the distribution.
| Marks obtained | 5 | 6 | 7 | 8 | 9 | 10 |
| No. of students | 3 | 9 | 6 | 4 | 2 | 1 |
Solution:
We write the marks in cumulative frequency table.
| Marks x | Frequency (f) | fx | Cumulative frequency |
| 5 | 3 | 15 | 3 |
| 6 | 9 | 54 | 12 |
| 7 | 6 | 42 | 18 |
| 8 | 4 | 32 | 22 |
| 9 | 2 | 18 | 24 |
| 10 | 1 | 10 | 25 |
| Total | Ʃf = 25 | Ʃfx = 171 |
Mean = Ʃfx/Ʃf
= 171/25
= 6.84
Hence the mean is 6.84.
Here number of observation, n = 25 which is odd.
Median = ((n+1)/2)th term
= (25+1)/2
= 26/2
= 13th term
= 7
Hence the median is 7.
Here the frequency corresponding to 6 is maximum.
Hence the mode is 6.
11. At a shooting competition, the scores of a competitor were as given below :
| Score | 0 | 1 | 2 | 3 | 4 | 5 |
| No. of shots | 0 | 3 | 6 | 4 | 7 | 5 |
(i) What was his modal score ?
(ii) What was his median score ?
(iii) What was his total score ?
(iv) What was his mean ?
Solution:
We write the marks in cumulative frequency table.
| Score x | No. of shots (f) | fx | Cumulative frequency |
| 0 | 0 | 0 | 0 |
| 1 | 3 | 3 | 3 |
| 2 | 6 | 12 | 9 |
| 3 | 4 | 12 | 13 |
| 4 | 7 | 28 | 20 |
| 5 | 5 | 25 | 25 |
| Total | Ʃf = 25 | Ʃfx = 80 |
(i) Here the frequency corresponding to 4 is maximum. 4 occurs 7 times.
Hence his modal score is 4.
(ii)Here number of observation, n = 25 which is odd.
Median = ((n+1)/2)th term
= (25+1)/2
= 26/2
= 13th term
= 3
Hence his median score is 3.
(iii)Total score = Ʃfx = 80
Hence his total score is 80.
(iv)Mean = Ʃfx/Ʃf
= 80/25
= 3.2
Hence his mean score is 3.2.
12. (i) Using step-deviation method, calculate the mean marks of the following distribution.
(ii) State the modal class.
| Class interval | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 | 75-80 | 80-85 | 85-90 |
| Frequency | 5 | 20 | 10 | 10 | 9 | 6 | 12 | 8 |
Solution:
(i) Class mark (xi) = (upper limit + lower limit)/2
Let assumed mean (A) = 67.5
Class size (h) = 5
| Class Interval | Frequency (fi) | Class mark (xi) | di = xi – A | ui = di/h | fiui |
| 50-55 | 5 | 52.5 | -15 | -3 | -15 |
| 55-60 | 20 | 57.5 | -10 | -2 | -40 |
| 60-65 | 10 | 62.5 | 5 | -1 | -10 |
| 65-70 | 10 | 67.5 | 10 | 0 | 0 |
| 70-75 | 9 | 72.5 | 15 | 1 | 9 |
| 75-80 | 6 | 77.5 | 20 | 2 | 12 |
| 80-85 | 12 | 82.5 | 25 | 3 | 36 |
| 85-90 | 8 | 87.5 | 30 | 4 | 32 |
| Total | ∑fi = 80 | ∑fiui = 24 |
By step deviation method, Mean = x̄ = A+h∑fiui /∑fi
= 67.5+5(24/80)
= 67.5+5×0.3
= 67.5+1.5
= 69
Hence the mean of the distribution is 69.
(ii) Modal class is the class with highest frequency.
Here the modal class is 55-60.
13. The following table gives the weekly wages (in Rs.) of workers in a factory :
| Weekly wages (in Rs) | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 | 75-80 | 80-85 | 85-90 |
| No. of workers | 5 | 20 | 10 | 10 | 9 | 6 | 12 | 8 |
Calculate:
(i) The mean.
(ii) the modal class
(iii) the number of workers getting weekly wages below Rs. 80.
(iv) the number of workers getting Rs. 65 or more but less than Rs. 85 as weekly wages.
Solution:
We write the given data in cumulative frequency table.
| Class Interval | Frequency (fi) | Class mark (xi) | Cumulative frequency | fixi |
| 50-55 | 5 | 52.5 | 5 | 262.5 |
| 55-60 | 20 | 57.5 | 25 | 1150 |
| 60-65 | 10 | 62.5 | 35 | 625 |
| 65-70 | 10 | 67.5 | 45 | 675 |
| 70-75 | 9 | 72.5 | 54 | 652.5 |
| 75-80 | 6 | 77.5 | 60 | 465 |
| 80-85 | 12 | 82.5 | 72 | 990 |
| 85-90 | 8 | 87.5 | 80 | 700 |
| Total | ∑fi = 80 | ∑fixi = 5520 |
(i) Mean = ∑fixi /∑fi
= 5520/80
= 69
Hence the mean is 69.
(ii) Modal class is the class with highest frequency.
Here the modal class is 55-60.
(iii) The number of workers getting weekly wages below Rs. 80 is 60.[Check the cumulative frequency column and class interval column. 60 workers get below Rs. 80]
(iv) The number of workers getting Rs. 65 or more but less than Rs. 85 as weekly wages = 72-35 = 37[Check the cumulative frequency column and class interval column. ]
Exercise 21.4
1. Draw a histogram for the following frequency distribution and find the mode from the graph :
| Class | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
| Frequency | 2 | 5 | 18 | 14 | 8 | 5 |
Solution:
Construct histogram using given data.
| Class | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
| Frequency | 2 | 5 | 18 | 14 | 8 | 5 |
Represent class on X-axis and frequency on Y-axis.
In the highest rectangle, draw two straight lines AC and BD.
P is the point of intersection.
Draw a vertical line through P to meet the X-axis at M.
The abscissa of M is 14.
Hence the mode is 14.
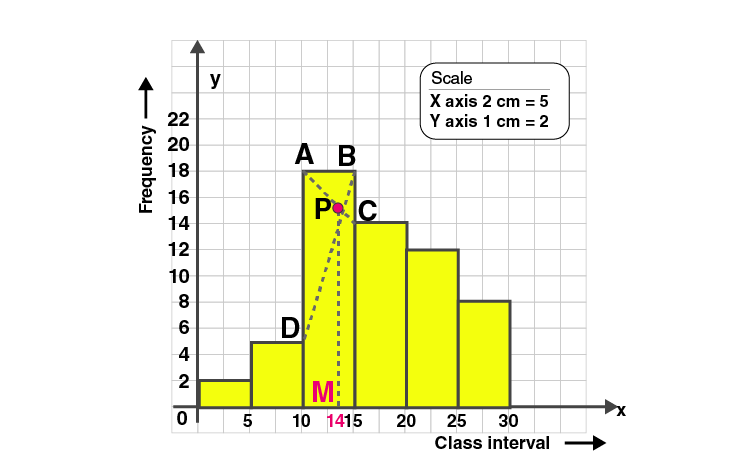
2. Find the modal height of the following distribution by drawing a histogram :
| Height (in cm) | 140-150 | 150-160 | 160-170 | 170-180 | 180-190 |
| No. of students | 7 | 6 | 4 | 10 | 2 |
Solution:
Construct histogram using given data.
| Height (in cm) | 140-150 | 150-160 | 160-170 | 170-180 | 180-190 |
| No. of students | 7 | 6 | 4 | 10 | 2 |
Represent height on X-axis and number of students on Y-axis.
Take scale: X axis : 2 cm = 10 (class interval)
Y axis : 1 cm = 1 (frequency)
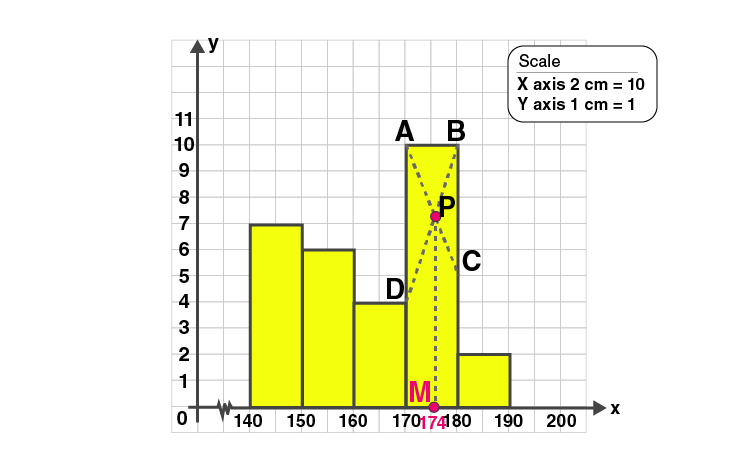
In the highest rectangle, draw two straight lines AC and BD.
P is the point of intersection.
Draw a vertical line through P to meet the X-axis at M.
The abscissa of M is 174.
Hence the mode is 174.
3. A Mathematics aptitude test of 50 students was recorded as follows :
| Marks | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of students | 4 | 8 | 14 | 19 | 5 |
Draw a histogram for the above data using a graph paper and locate the mode. (2011)
Solution:
Construct histogram using given data.
| Marks | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of students | 4 | 8 | 14 | 19 | 5 |
Represent marks on X-axis and number of students on Y-axis.
Take scale: X axis : 2 cm = 10 (class interval)
Y axis : 1 cm = 1 (frequency)
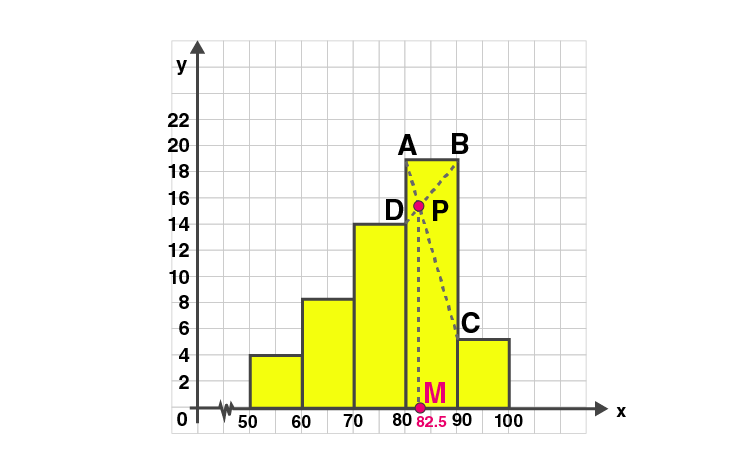
In the highest rectangle, draw two straight lines AC and BD.
P is the point of intersection.
Draw a vertical line through P to meet the X-axis at M.
The abscissa of M is 82.5.
Hence the mode is 82.5.
4. Draw a histogram and estimate the mode for the following frequency distribution :
| Classes | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Frequency | 2 | 8 | 10 | 5 | 4 | 3 |
Solution:
Construct histogram using given data.
| Classes | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Frequency | 2 | 8 | 10 | 5 | 4 | 3 |
Represent classes on X-axis and frequency on Y-axis.
Take scale: X axis : 2 cm = 10 (class interval)
Y axis : 1 cm = 1 (frequency)
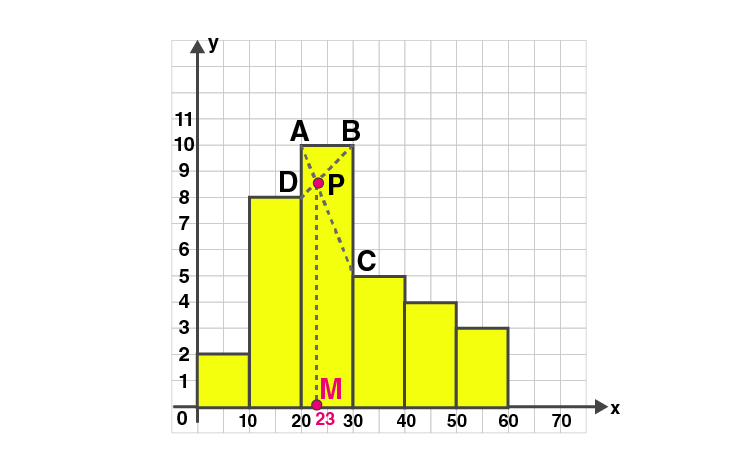
In the highest rectangle, draw two straight lines AC and BD.
P is the point of intersection.
Draw a vertical line through P to meet the X-axis at M.
The abscissa of M is 23.
Hence the mode is 23.
5. IQ of 50 students was recorded as follows.
| IQ score | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 |
| No. of students | 6 | 9 | 16 | 13 | 4 | 2 |
Draw a histogram for the above data and estimate the mode.
Solution:
Construct histogram using given data.
Represent classes on X-axis and frequency on Y-axis.
Take scale: X axis : 1 cm = 10 (class interval)
Y axis : 1 cm = 1 (frequency)

In the highest rectangle, draw two straight lines AB and CD.
M is the point of intersection.
Draw a vertical line through M to meet the X-axis at L.
The abscissa of L is 107.
Hence the mode is 107.
6. Use a graph paper for this question. The daily pocket expenses of 200 students in a school are given below:
| Pocket expenses (in Rs) | Number of students(Frequency ) |
| 0-5 | 10 |
| 5-10 | 14 |
| 10-15 | 28 |
| 15-20 | 42 |
| 20-25 | 50 |
| 25-30 | 30 |
| 30-35 | 14 |
| 35-40 | 12 |
Draw a histogram representing the above distribution and estimate the mode from the graph.
Solution:
Construct histogram using given data.
Represent classes on X-axis and frequency on Y-axis.
Take scale: X axis : 2 cm = 5 (class interval)
Y axis : 1 cm = 5 (frequency)
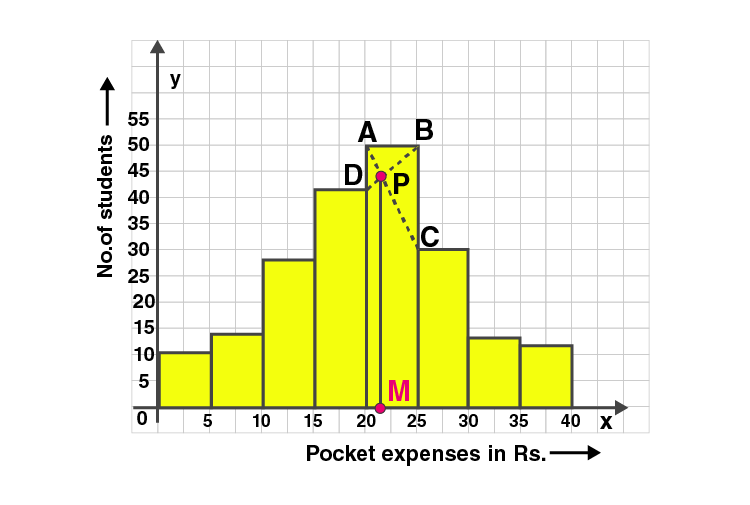
In the highest rectangle, draw two straight lines AC and BD.
P is the point of intersection.
Draw a vertical line through P to meet the X-axis at M.
The abscissa of M is 21.
Hence the mode is 21.
7. Draw a histogram for the following distribution :
| Wt. in kg | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 | 65-69 |
| No. of students | 2 | 8 | 12 | 10 | 6 | 4 |
Hence estimate the modal weight.
Solution:
The given distribution is not continuous.
Adjustment factor = (45-44)/2 = ½ = 0.5
We subtract 0.5 from lower limit of the class interval and add 0.5 to upper limit.
So the new table in continuous form is given below.
| Weight in kg | Number of students(Frequency ) |
| 39.5-44.5 | 2 |
| 44.5-49.5 | 8 |
| 49.5-54.5 | 12 |
| 54.5-59.5 | 10 |
| 59.5-64.5 | 6 |
| 64.5-69.5 | 4 |
Construct histogram using given data.
Represent weight on X-axis and no. of students on Y-axis.
Take scale: X axis : 2 cm = 5 (class interval)
Y axis : 1 cm = 1 (frequency)

In the highest rectangle, draw two straight lines AC and BD.
P is the point of intersection.
Draw a vertical line through P to meet the X-axis at M.
The abscissa of M is 52.75.
Hence the mode is 52.75.
8. Find the mode of the following distribution by drawing a histogram
| Mid value | 12 | 18 | 24 | 30 | 36 | 42 | 48 |
| Frequency | 20 | 12 | 8 | 24 | 16 | 8 | 12 |
Also state the modal class.
Solution:
| Mid value | Frequency |
| 12 | 20 |
| 18 | 12 |
| 24 | 8 |
| 30 | 24 |
| 36 | 16 |
| 42 | 8 |
| 48 | 12 |
Here mid value and frequency is given.
We can find the class size, h by subtracting second mid value from first mid value.
h = 18-12 = 6
So to find the lower limit of class interval, we subtract h/2 to the mid value.
To find the upper limit of class interval, we add h/2 to the mid value.
Here h/2 = 6/2 = 3
So lower limit = 12-3 = 9
Upper limit = 12+3 = 15
So the class interval is 9-15
Likewise we find the class interval of other values.
| Mid value | Class interval | Frequency |
| 12 | 9-15 | 20 |
| 18 | 15-21 | 12 |
| 24 | 21-27 | 8 |
| 30 | 27-33 | 24 |
| 36 | 33-39 | 16 |
| 42 | 39-45 | 8 |
| 48 | 45-51 | 12 |
Construct histogram using given data.
Take scale: X axis : 2 cm = 6 (class interval)
Y axis : 1 cm = 2 (frequency)

In the highest rectangle, draw two straight lines AB and CD.
M is the point of intersection.
Draw a vertical line through M to meet the X-axis at L.
The abscissa of L is 30.5.
Hence the mode is 30.5.
Modal class is the class with highest frequency.
Hence the modal class is 27-33.
Exercise 21.5
1.Draw an ogive for the following frequency distribution:
| Height ( in cm ) | 150-160 | 160-170 | 170-180 | 180-190 | 190-200 |
| No. of students | 8 | 3 | 4 | 10 | 2 |
Solution:
We write the given data in cumulative frequency table.
| Height in cm | No of students | Cumulative frequency |
| 150-160 | 8 | 8 |
| 160-170 | 3 | 11 |
| 170-180 | 4 | 15 |
| 180-190 | 10 | 25 |
| 190-200 | 2 | 27 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis).
Plot the points (160, 8), (170, 11), (180, 15), (190, 25) and (200, 27) on the graph.
Join the points with the free hand. We get an ogive as shown:

2. Draw an ogive for the following data:
| Class intervals | 1-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 |
| Frequency | 3 | 5 | 8 | 7 | 6 | 2 |
Solution:
The given distribution is not continuous.
Adjustment factor = (11-10)/2 = ½ = 0.5
We subtract 0.5 from lower limit of the class interval and add 0.5 to upper limit.
So the new table in continuous form is given below.
We write the given data in cumulative frequency table.
| Class intervals | frequency | Cumulative frequency |
| 0.5-10.5 | 3 | 3 |
| 10.5-20.5 | 5 | 8 |
| 20.5-30.5 | 8 | 16 |
| 30.5-40.5 | 7 | 23 |
| 40.5-50.5 | 6 | 29 |
| 50.5-60.5 | 2 | 31 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis).
Plot the points (10.5, 3), (20.5, 8), (30.5, 16), (40.5, 23) , (50.5, 29) and (60.5, 31) on the graph.
Join the points with the free hand. We get an ogive as shown:
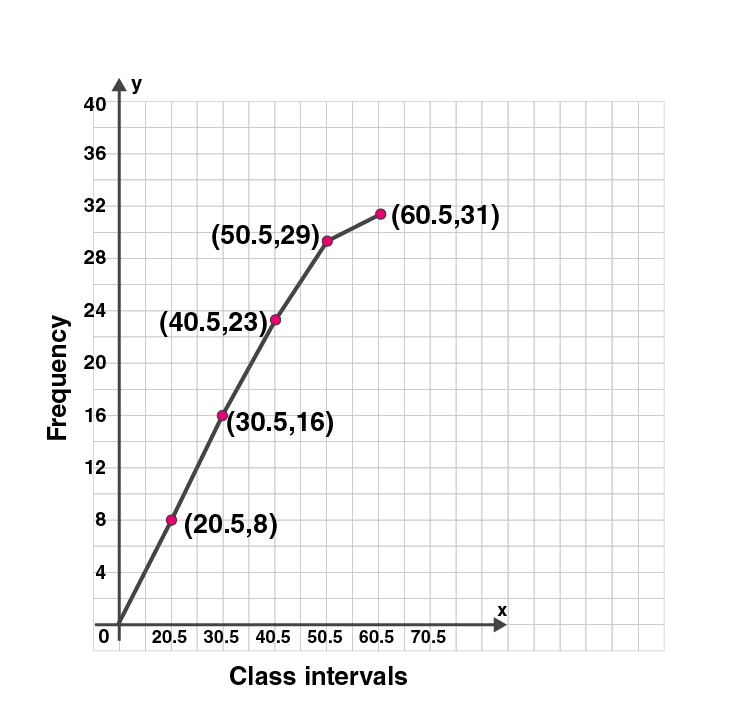
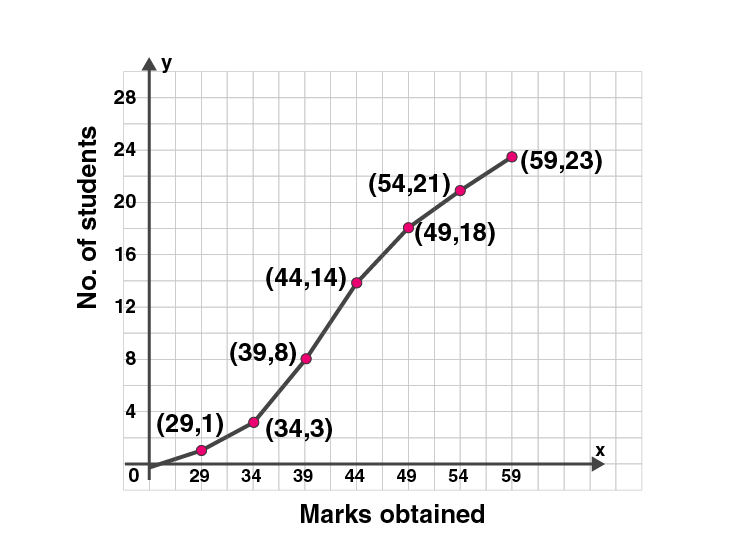
3. Draw a cumulative frequency curve for the following data:
| Marks obtained | 24-29 | 29-34 | 34-39 | 39-44 | 44-49 | 49-54 | 54-59 |
| No. of students | 1 | 2 | 5 | 6 | 4 | 3 | 2 |
Solution:
We write the given data in cumulative frequency table.
| Marks obtained | No of students | Cumulative frequency |
| 24-29 | 1 | 1 |
| 29-34 | 2 | 3 |
| 34-39 | 5 | 8 |
| 39-44 | 6 | 14 |
| 44-49 | 4 | 18 |
| 49-54 | 3 | 21 |
| 54-59 | 2 | 23 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis).
Plot the points (29, 1), (34, 3), (39, 8), (44, 14), (49, 18) , (54, 21) and (59, 23) on the graph.
Join the points with the free hand. We get an ogive as shown:
Exercise 21.6
1. The following table shows the distribution of the heights of a group of a factory workers.
| Height ( in cm ) | 150-155 | 155-160 | 160-165 | 165-170 | 170-175 | 175-180 | 180-185 |
| No. of workers | 6 | 12 | 18 | 20 | 13 | 8 | 6 |
(i) Determine the cumulative frequencies.
(ii) Draw the cumulative frequency curve on a graph paper. Use 2 cm = 5 cm height on one axis and 2 cm = 10 workers on the other.
(iii) From your graph, write down the median height in cm.
Solution:
(i) We write the given data in cumulative frequency table.
| Height in cm | No of workers f | Cumulative frequency |
| 150-155 | 6 | 6 |
| 155-160 | 12 | 18 |
| 160-165 | 18 | 36 |
| 165-170 | 20 | 56 |
| 170-175 | 13 | 69 |
| 175-180 | 8 | 77 |
| 180-185 | 6 | 83 |
(ii)Plot the points (155, 6), (160, 18), (165, 36), (170, 56), (175, 69), (180, 77) and (185, 83) on the graph.
Join the points with the free hand. We get an ogive as shown:
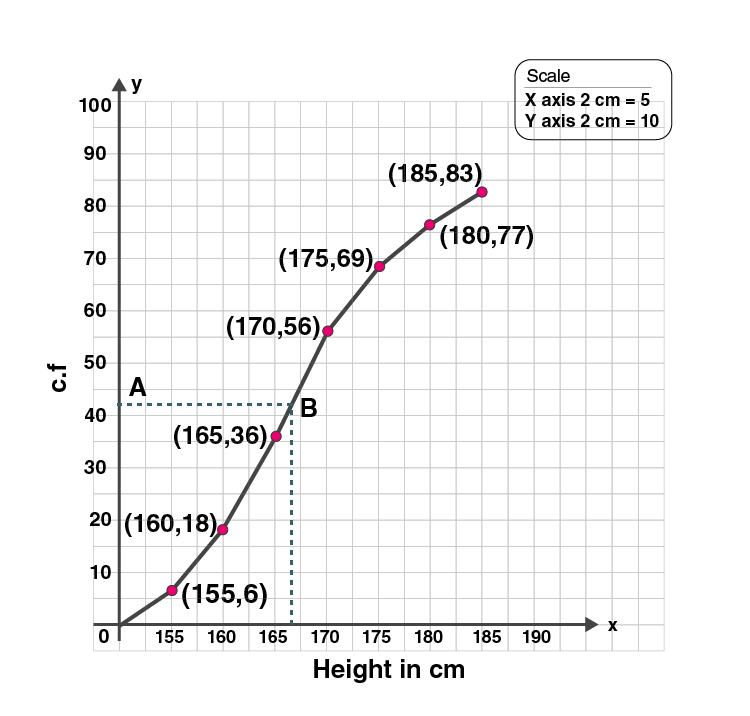
(iii)Here n = 83 , which is odd.
So median = ((n+1)/2)th observation
= ((83+1)/2)th observation
= (84/2)th observation
= 42th observation
Take a point A(42) on Y-axis. From A, draw a horizontal line parallel to X-axis meeting the curve at B. From B draw a line perpendicular on the x-axis which meets it at C.
C is the median which is 166.5 cm.
2. Using the data given below construct the cumulative frequency table and draw the-Ogive. From the ogive determine the median.
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| No. of students | 3 | 8 | 12 | 14 | 10 | 6 | 5 | 2 |
Solution:
We write the given data in cumulative frequency table.
| Marks | No of students f | Cumulative frequency c.f |
| 0-10 | 3 | 3 |
| 10-20 | 8 | 11 |
| 20-30 | 12 | 23 |
| 30-40 | 14 | 37 |
| 40-50 | 10 | 47 |
| 50-60 | 6 | 53 |
| 60-70 | 5 | 58 |
| 70-80 | 2 | 60 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis),
Plot the points (10, 3), (20, 11), (30, 23), (40, 37), (50, 47), (60, 53), (70, 58) and (80, 60) on the graph.
Join the points with the free hand. We get an ogive as shown:

Here number of observations, n = 60 which is even.
So median = ( n/2) th term
= (60/2 th term
= 30 th term
Mark a point A(30) on Y-axis. From A, draw a horizontal line parallel to X-axis meeting the curve at P. From P draw a line perpendicular on the x-axis which meets it at Q.
Q is the median .
Q = 35
Hence the median is 35 .
3. Use graph paper for this question. The following table shows the weights in gm of a sample of 100 potatoes taken from a large consignment:
| Weight (gm) | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 |
| Frequency | 8 | 10 | 12 | 16 | 18 | 14 | 12 | 10 |
(i) Calculate the cumulative frequencies.
(ii) Draw the cumulative frequency curve and from it determine the median weight of the potatoes. (1996)
Solution:
(i)We write the given data in cumulative frequency table.
| Marks | frequency f | Cumulative frequency c.f |
| 50-60 | 8 | 8 |
| 60-70 | 10 | 18 |
| 70-80 | 12 | 30 |
| 80-90 | 16 | 46 |
| 90-100 | 18 | 64 |
| 100-110 | 14 | 78 |
| 110-120 | 12 | 90 |
| 120-130 | 10 | 100 |
(ii)To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis),
Plot the points (60, 8), (70, 18), (80, 30), (90, 46), (100, 64), (110, 78), (120, 90) and (130, 100) on the graph.
Join the points with the free hand. We get an ogive as shown:
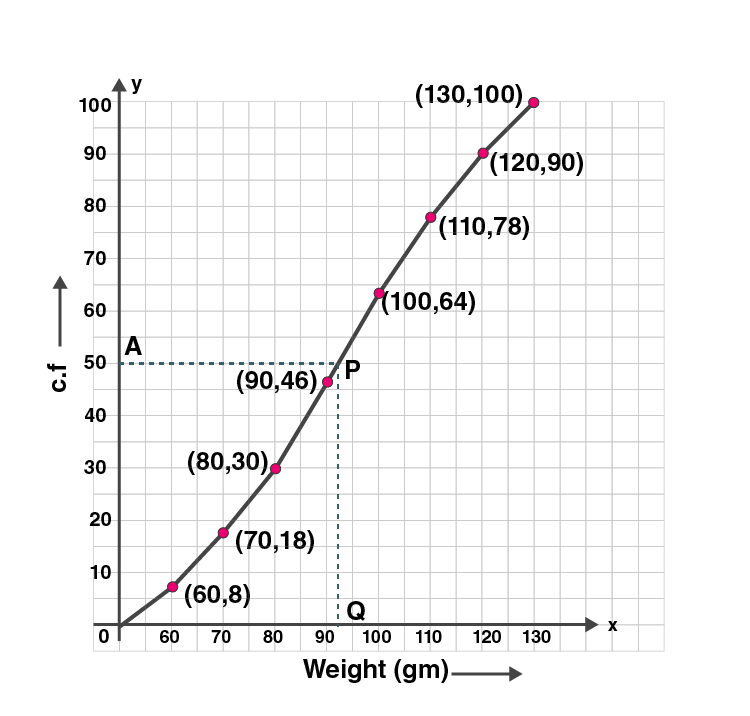
Here n = 100 which is even.
So median = ( n/2 th term)
= (100/2 th term)
= (50 th term)
Now mark a point A (50) on the Y-axis and from A draw a line parallel to X-axis meeting the curve at P. From P, draw a perpendicular on x-axis meeting it at Q.
Q is the median.
Q = 93 gm.
Hence the median is 93.
4. Attempt this question on graph paper.
| Age( yrs) | 5-15 | 15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
| No. of casualities due to accidents | 6 | 10 | 15 | 13 | 24 | 8 | 7 |
(i) Construct the ‘less than’ cumulative frequency curve for the above data, using 2 cm = 10 years, on one axis and 2 cm = 10 casualties on the other.
(ii) From your graph determine
(1) the median and (2) the upper quartile
Solution:
(i)We write the given data in cumulative frequency table.
| Age (yrs) | No of casualities due to accidents f | Cumulative frequency c.f |
| 5-15 | 6 | 6 |
| 15-25 | 10 | 16 |
| 25-35 | 15 | 31 |
| 35-45 | 13 | 44 |
| 45-55 | 24 | 68 |
| 55-65 | 8 | 76 |
| 65-75 | 7 | 83 |
(ii)To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis),
Plot the points (15, 6), (25, 16), (35, 31), (45, 44), (55, 68), (65, 76) and (75, 83) on the graph.
Join the points with the free hand. We get an ogive as shown:
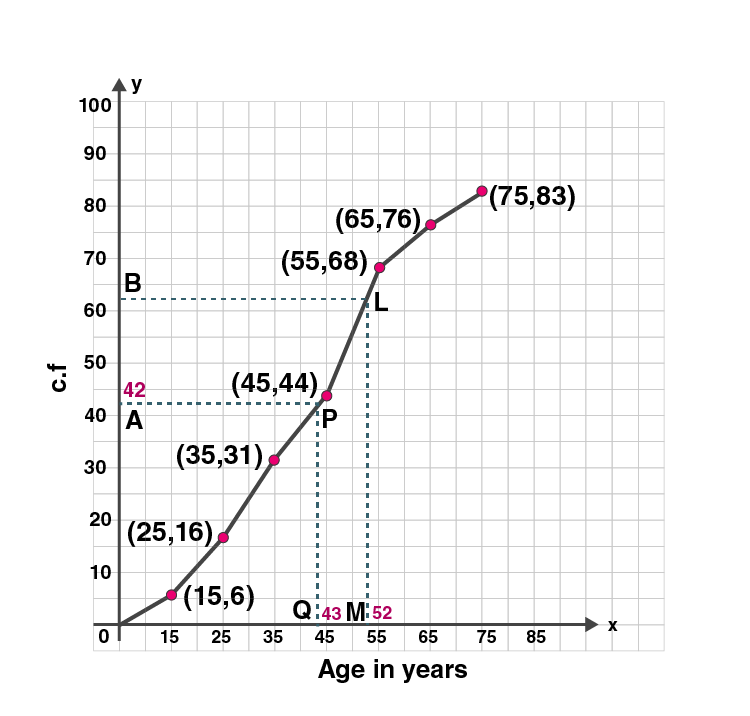
(ii)(1). Here n = 83, which is odd.
So median = (n+1)/2)th term
= ((83+1)/2)
= 84/2
= 42
Now mark a point A (42) on the Y-axis and from A draw a line parallel to X-axis meeting the curve at P. From P, draw a perpendicular on x-axis meeting it at Q.
Q is the median.
Q = 43
Hence the median is 43.
(ii)(2). Upper quartile = (3(n+1)/4)
= (3×(83+1)/4)
= (3×(84)/4)
= 63
Now mark a point B (63) on the Y-axis and from A draw a line parallel to X-axis meeting the curve at L. From L, draw a perpendicular on x-axis meeting it at M.
M = 52
Hence the upper quartile is 52.
5. The weight of 50 workers is given below:
| Weight in kg | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 |
| No. of workers | 4 | 7 | 11 | 14 | 6 | 5 | 3 |
Draw an ogive of the given distribution using a graph sheet. Take 2 cm = 10 kg on one axis , and 2 cm = 5 workers along the other axis.
Use a graph to estimate the following:
(i) the upper and lower quartiles.
(ii) if weighing 95 kg and above is considered overweight find the number of workers who are overweight. (2015)
Solution:
We write the given data in cumulative frequency table.
| Weight in kg | No of workers f | Cumulative frequency c.f |
| 50-60 | 4 | 4 |
| 60-70 | 7 | 11 |
| 70-80 | 11 | 22 |
| 80-90 | 14 | 36 |
| 90-100 | 6 | 42 |
| 100-110 | 5 | 47 |
| 110-120 | 3 | 50 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis),
Plot the points (60, 4), (70, 11), (80, 22), (90, 36), (100, 42), (110, 47) and (120, 50) on the graph.
Join the points with the free hand. We get an ogive as shown:
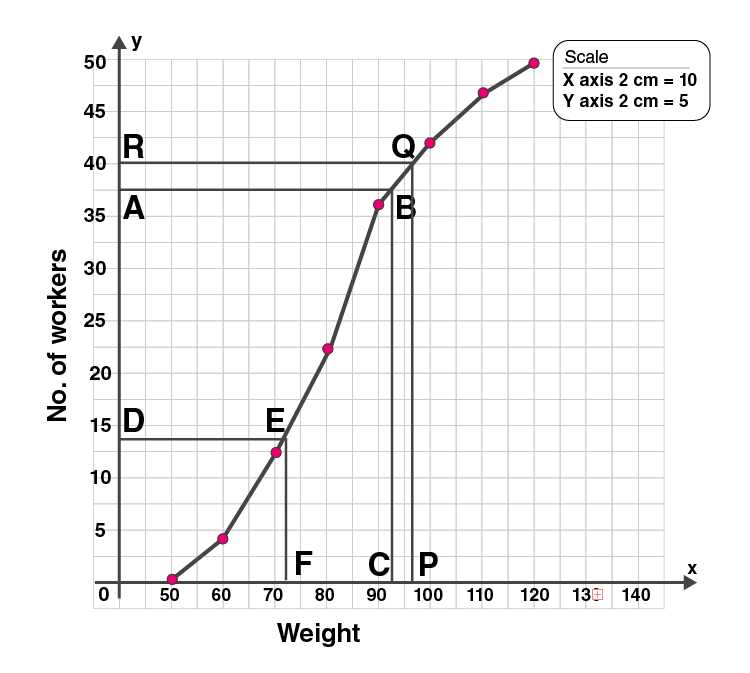
(i)Here n = 50, which is even.
Upper quartile = 3n/4
= 3×50/4
= 150/4
= 37.5
Now mark a point A (37.5) on the Y-axis and from A draw a line parallel to X-axis meeting the curve at B. From B, draw a perpendicular on x-axis meeting it at C.
C = 92.5
Hence the upper quartile is 92.5 kg.
Lower quartile, Q1 = (n/4) th term
= 50/4
= 12.5
Now mark a point D(12.5) on the Y-axis and from D draw a line parallel to X-axis meeting the curve at E. From E, draw a perpendicular on x-axis meeting it at F.
F = 72
Hence the lower quartile is 72 kg.
(ii) Mark on the graph point P which is 95 kg on X axis.
Through P draw a vertical line to meet the ogive at Q. Through Q, draw a horizontal line to meet y-axis at R.
The ordinate of point R represents 40 workers on the y-axis .
The number of workers who are 95 kg and above = Total number of workers – number of workers of weight less than 95 kg = 50-40 = 10
6. The table shows the distribution of scores obtained by 160 shooters in a shooting competition. Use a graph sheet and draw an ogive for the distribution. (Take 2 cm = 10 scores on the x-axis and 2 cm = 20 shooters on the y-axis)
| Scores | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of shooters | 9 | 13 | 20 | 26 | 30 | 22 | 15 | 10 | 8 | 7 |
Use your graph to estimate the following:
(i) The median.
(ii) The interquartile range.
(iii) The number of shooters who obtained a score of more than 85%.
Solution:
We write the given data in cumulative frequency table.
| Scores | No of shooters f | Cumulative frequency c.f |
| 0-10 | 9 | 9 |
| 10-20 | 13 | 22 |
| 20-30 | 20 | 42 |
| 30-40 | 26 | 68 |
| 40-50 | 30 | 98 |
| 50-60 | 22 | 120 |
| 60-70 | 15 | 135 |
| 70-80 | 10 | 145 |
| 80-90 | 8 | 153 |
| 90-100 | 7 | 160 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis),
Plot the points (10, 9), (20, 22), (30, 42), (40, 68), (50, 98), (60, 120), (70, 135), (80, 145), (90, 153) and (100, 160) on the graph.
Join the points with the free hand. We get an ogive as shown:

(i)Here n = 160, which is even.
So median = n/2 = 80
Now mark a point A(80) on the Y-axis and from A draw a line parallel to X-axis meeting the curve at B. From P, draw a perpendicular on x-axis meeting it at C.
C is the median.
C = 44
(ii) lower quartile, Q1 = (n/4)th term
= 160/4
= 40
Now mark a point D(40) on the Y-axis and from that point draw a line parallel to X-axis meeting the curve at E. From E, draw a perpendicular on x-axis meeting it at F.
F = 29
So Q1= 29
Upper quartile, Q3 = (3n/4)th term
= 3×160/4
= 3×40
= 120
Mark a point P(120) on the Y-axis and from that point draw a line parallel to X-axis meeting the curve at Q. From Q, draw a perpendicular on x-axis meeting it at R.
R = 60
So Q3 = 60
Inter quartile range = Q3– Q1
= 60-29
= 31
Hence the Inter quartile range is 31.
(iii) Mark a point Z(85) on the X axis.
From Z on X-axis, draw a perpendicular to it meeting the curve at Y. From Y, draw a line parallel to X-axis meeting Y-axis at X. X is the required point which is 150.
Number of shooters getting more than 85% scores = Total number of shooters – number of shooters who got till 85% = 160-150 = 10.
Hence the number of shooters getting more than 85% scores is 10.
7. The daily wages of 80 workers in a project are given below
| Wages in Rs | 400-450 | 450-500 | 500-550 | 550-600 | 600-650 | 650-700 | 700-750 |
| No. of workers | 2 | 6 | 12 | 18 | 24 | 13 | 5 |
Use a graph paper to draw an ogive for the above distribution. ( a scale of 2 cm = Rs 50 on x- axis and 2 cm = 10 workers on y-axis). your ogive to estimate
(i) the median wage of the workers.
(ii) the lower quartile wage of the workers.
(iii) the number of workers who earn more than Rs 625 daily. (2017)
Solution:
We write the given data in cumulative frequency table.
| Wages in Rs. | No of workers f | Cumulative frequency c.f |
| 400-450 | 2 | 2 |
| 450-500 | 6 | 8 |
| 500-550 | 12 | 20 |
| 550-600 | 18 | 38 |
| 600-650 | 24 | 62 |
| 650-700 | 13 | 75 |
| 700-750 | 5 | 80 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis),
Plot the points (450, 9), (500, 22), (550, 42), (600, 68), (650, 98), (700, 120) and (750, 135) on the graph.
Join the points with the free hand. We get an ogive as shown:

(i)Here n = 80.
Median = (n/2)th term
= 80/2
= 40th term
Mark a point (40) on Y axis. Draw a line from that point parallel to X axis. Let it meet the curve at A.
Draw a perpendicular from A to meet X axis at B.
The value of B is 604.
Hence the median is 604.
(ii)Lower quartile, Q1 = (n/4)th term
= 80/4
= 20th term
= 550 [from graph]
(iii) Draw a vertical line through the point 625 on X axis. which meets the graph at point C. From C, draw a horizontal line which meets the y-axis at the mark of 50.
Thus, number of workers that earn more Rs 625 daily = Total no. of workers – no. of workers who earn upto 625
= 80-50 = 30
8. Marks obtained by 200 students in an examination are given below
| marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of students | 5 | 11 | 10 | 20 | 28 | 37 | 40 | 29 | 14 | 6 |
Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis.
Using the graph, determine
(i) The median marks.
(ii) The number of students who failed if minimum marks required to pass is 40.
(iii) If scoring 85 and more marks is considered as grade one, find the number of students who secured grade one in the examination.
Solution:
We write the given data in cumulative frequency table.
| Marks | No of students f | Cumulative frequency c.f |
| 0-10 | 5 | 5 |
| 10-20 | 11 | 16 |
| 20-30 | 10 | 26 |
| 30-40 | 20 | 46 |
| 40-50 | 28 | 74 |
| 50-60 | 37 | 111 |
| 60-70 | 40 | 151 |
| 70-80 | 29 | 180 |
| 80-90 | 14 | 194 |
| 90-100 | 6 | 200 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis),
Plot the points (10, 5), (20, 16), (30, 26), (40, 46), (50, 74), (60, 111) , (70, 151) (80, 180) (90, 194) and (100, 200) on the graph.
Join the points with the free hand. We get an ogive as shown:

(i)Here n= 200
Median = (n/2)th term
= 200/2
= 100th term
= 57 [from graph]
(ii)number of students failed if minimum marks required to pass is 40 = 44 [from graph]
(iii)Number of students who got grade 1 = number of students who scored 85 and more
= 200-188
= 12[From graph]
9. The monthly income of a group of 320 employees in a company is given below
| Monthly income | No. of employees |
| 6000-7000 | 20 |
| 7000-8000 | 45 |
| 8000-9000 | 65 |
| 9000-10000 | 95 |
| 10000-11000 | 60 |
| 11000-12000 | 30 |
| 12000-13000 | 5 |
Draw an ogive of the given distribution on a graph sheet taking 2 cm = Rs. 1000 on one axis and 2 cm = 50 employees on the other axis.
From the graph determine
(i) the median wage.
(ii) the number of employees whose income is below Rs. 8500.
(iii) If the salary of a senior employee is above Rs. 11500, find the number of senior employees in the company.
(iv) the upper quartile.
Solution:
We write the given data in cumulative frequency table.
| Monthly income | No. of employees | Cumulative frequency c.f |
| 6000-7000 | 20 | 20 |
| 7000-8000 | 45 | 65 |
| 8000-9000 | 65 | 130 |
| 9000-10000 | 95 | 225 |
| 10000-11000 | 60 | 285 |
| 11000-12000 | 30 | 315 |
| 12000-13000 | 5 | 320 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis),
Plot the points (7000, 20), (8000, 65), (9000, 130), (10000, 225), (11000, 285), (12000, 315) and (13000, 320) on the graph.
Join the points with the free hand. We get an ogive as shown:
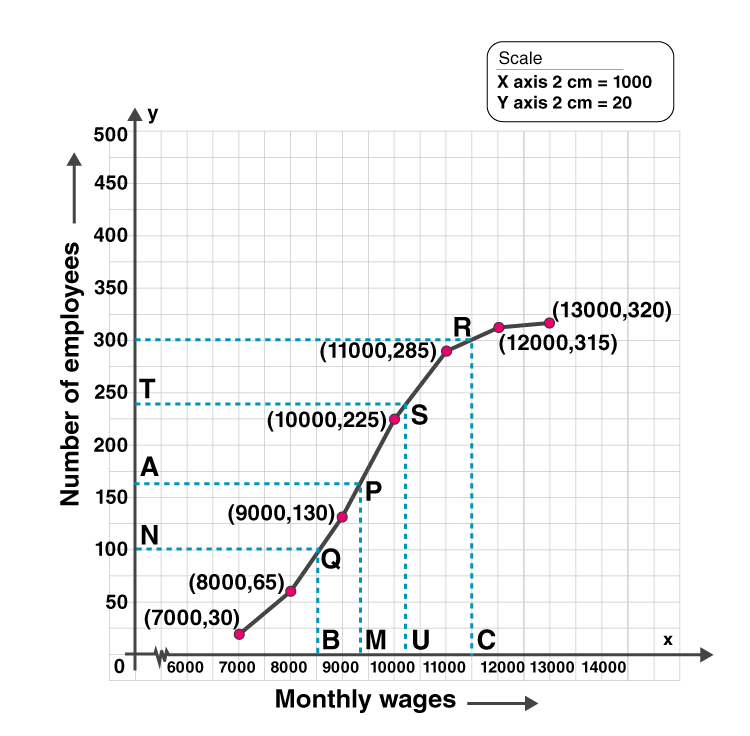
(i)here n = 320
Median = (n/2)th term
= 320/2
= 160th term
Mark the point A(160) on Y axis.
Draw a line parallel to x axis from that point.
Let it meet the curve at P.
Draw a perpendicular from P to X axis which meets at M.
M is the median.
Here median is 9300. [from graph]
(ii)Mark the point B(8500) on X axis.
Draw a line parallel to Y axis which meets curve at Q.
From Q draw a line parallel to X axis which meets Y axis at N.
N = 98
number of employees whose income is below 8500 = 98
(iii) Mark the point C(11500) on the x-axis.
Draw a line perpendicular to x-axis meeting the curve at R.
From R, draw a line parallel to x-axis meeting y-axis at L which is 300
No. of employees getting more than Rs. 11500 = 320-300 = 20
(iv)upper quartile = 3n/4
= 3×320/4
= 240
Mark the point T(240) on Y axis.
From that point on y-axis, draw a line perpendicular on the x-axis which meets the curve at S.
From S, draw a perpendicular on x-axis meeting it at U, which is 10250.
Hence upper quartile is 10250.
10. Using a graph paper, draw an ogive for the following distribution which shows a record of the weight in kilograms of 200 students
| Weight | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 | 75-80 |
| Frequency | 5 | 17 | 22 | 45 | 51 | 31 | 20 | 9 |
Use your ogive to estimate the following:
(i) The percentage of students weighing 55 kg or more.
(ii) The weight above which the heaviest 30% of the students fall,
(iii) The number of students who are :
1. under-weight and
2. over-weight, if 55.70 kg is considered as standard weight.
Solution:
We write the given data in cumulative frequency table.
| Weight | Frequency | Cumulative frequency c.f |
| 40-45 | 5 | 5 |
| 45-50 | 17 | 22 |
| 50-55 | 22 | 44 |
| 55-60 | 45 | 89 |
| 60-65 | 51 | 140 |
| 65-70 | 31 | 171 |
| 70-75 | 20 | 191 |
| 75-80 | 9 | 200 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis),
Plot the points (45, 5), (50, 22), (55, 44), (60, 89), (65, 140), (70, 171), (75, 191) and (80, 200) on the graph.
Join the points with the free hand. We get an ogive as shown:

(i)Total number of students = 200
The number of students weighing 55 kg or more = 200-44 = 156 [From the graph]
Percentage = (156/200)×100
= 156/2
= 78%.
(ii)30% of 200 = (30/100)×200
= 30×2
= 60
No of heaviest students = 31+20+9 = 60
60 students fall above 65 kg.
(iii)If 55.70 kg is the standard weight,
No. of students who are under weight = 47 [from graph]
No. of students who are overweight = 200-47 = 153
11. The marks obtained by 100 students in a Mathematics test are given below
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of students | 3 | 7 | 12 | 17 | 23 | 14 | 9 | 6 | 5 | 4 |
Draw an ogive on a graph sheet and from it determine the :
(i) median
(ii) lower quartile
(iii) number of students who obtained more than 85% marks in the test.
(iv) number of students who did not pass in the test if the pass percentage was 35.
Solution:
We write the given data in cumulative frequency table.
| Marks | No. of students | Cumulative frequency c.f |
| 0-10 | 3 | 3 |
| 10-20 | 7 | 10 |
| 20-30 | 12 | 22 |
| 30-40 | 17 | 39 |
| 40-50 | 23 | 62 |
| 50-60 | 14 | 76 |
| 60-70 | 9 | 85 |
| 70-80 | 6 | 91 |
| 80-90 | 5 | 96 |
| 90-100 | 4 | 100 |
Plot the points (10, 3), (20, 10), (30, 22), (40, 39), (50, 62), (60, 76), (70, 85), (80, 91), (90, 96) and (100, 100) on the graph.
Join the points with the free hand. We get an ogive as shown:

(i)Here n = 100
Median = n/2
= 50 th term
Mark a point A(50) on Y axis. Draw a line parallel to X axis from A.
Let it meet the curve at B. From B draw a perpendicular which meets X axis at C.
The point C is 45.
Hence median is 45.
(ii)Lower quartile = n/4
= 100/4
= 25th term
Mark a point P (25) on Y axis. Draw a line parallel to X axis from that point.
Let it meet the curve at Q. From that point draw a perpendicular which meets X axis at R.
The point R is 32.
Hence lower quartile is 32.
(iii)no. of students who obtained more than 85% = 100-94 = 6 [from graph]
(iv)No of students who failed if 35% is the pass percentage = 25 [from graph]
12. The marks obtained by 120 students in a Mathematics test are-given below
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of students | 5 | 9 | 16 | 22 | 26 | 18 | 11 | 6 | 4 | 3 |
Draw an ogive for the given distribution on a graph sheet. Use a suitable scale for ogive to estimate the following:
(i) the median
(ii) the lower quartile
(iii) the number of students who obtained more than 75% marks in the test.
(iv) the number of students who did not pass in the test if the pass percentage was 40. (2002)
Solution:
We write the given data in cumulative frequency table.
| Marks | No. of students | Cumulative frequency c.f |
| 0-10 | 5 | 5 |
| 10-20 | 9 | 14 |
| 20-30 | 16 | 30 |
| 30-40 | 22 | 52 |
| 40-50 | 26 | 78 |
| 50-60 | 18 | 96 |
| 60-70 | 11 | 107 |
| 70-80 | 6 | 113 |
| 80-90 | 4 | 117 |
| 90-100 | 3 | 120 |
Plot the points (10, 5), (20, 14), (30, 30), (40, 52), (50, 78), (60, 96), (70, 107), (80, 113), (90, 117) and (100, 120) on the graph.
Join the points with the free hand. We get an ogive as shown:
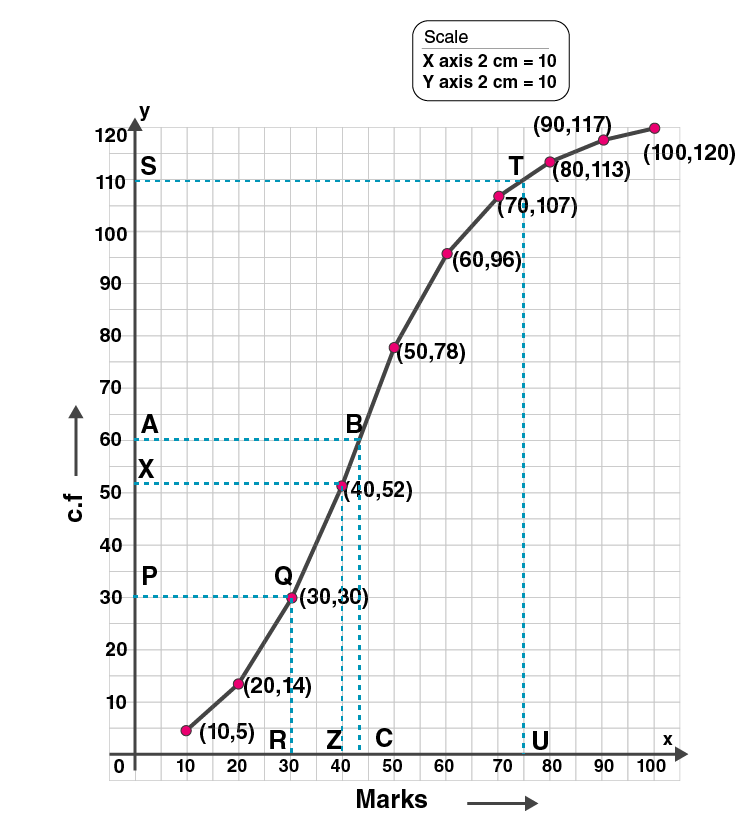
(i)Here n = 120
Median = (n/2)th term
= 120/2
= 60th term
Mark point A(60) on Y axis. Draw a line parallel to X axis from A.
Let it meet the curve at B. Draw a straight line from B to X axis which meets at C.
C = 50
Hence median is 50.
(ii)Lower quartile = (n/4)th term
= 120/4
= 30th term
Mark a point P (30) on Y axis. Draw a line parallel to X axis from that point.
Let it meet the curve at Q. From that point draw a perpendicular which meets X axis at R.
The point R is 30.
Hence lower quartile is 30.
(iii)Mark a point U(75) on X axis.
Draw a line parallel to Y axis which meets curve at T.
From T, draw a line parallel to X axis to meet Y axis at S.
S = 110
No. of students who obtained more than 75% = 120-110 = 10
(iv) Mark a point Z(40) on X axis.
Draw a line parallel to Y axis which meets curve at Y.
From Y, draw a line parallel to X axis to meet Y axis at X.
X = 52
No of students who failed if 40% is the pass percentage is 52.
13. The following distribution represents the height of 160 students of a school.
| Height | 140-145 | 145-150 | 150-155 | 155-160 | 160-165 | 165-170 | 170-175 | 175-180 |
| No. of students | 12 | 20 | 30 | 38 | 24 | 16 | 12 | 8 |
Draw an ogive for the given distribution taking 2 cm = 5 cm of height on one axis and 2 cm = 20 students on the other axis.
Using the graph, determine :
(i)The median height.
(ii)The inter quartile range.
(iii) The number of students whose height is above 172 cm.
Solution:
We write the given data in cumulative frequency table.
| Height | No. of students | Cumulative frequency c.f |
| 140-145 | 12 | 12 |
| 145-150 | 20 | 32 |
| 150-155 | 30 | 62 |
| 155-160 | 38 | 100 |
| 160-165 | 24 | 124 |
| 165-170 | 16 | 140 |
| 170-175 | 12 | 152 |
| 175-180 | 8 | 160 |
Plot the points (145, 12), (150, 32), (155, 62), (160, 100), (165, 124), (170, 140), (175, 152), and (180, 160) on the graph.
Join the points with the free hand. We get an ogive as shown:

(i)Here n = 160
Median = (n/2)th term
= 160/2
= 80th term
Mark point A(80) on Y axis. Draw a line parallel to X axis from A.
Let it meet the curve at B. Draw a straight line from B to X axis which meets at C.
C = 157.5
Hence median is 157.5.
(ii) Lower quartile , Q1 = (n/4)th term
= 160/4
= 40th term
Proceeding in the same way mentioned in (i),
we get lower quartile = 152 [Point R]
Upper quartile, Q3 = 3n/4
= 3×160/4
= 3×40
= 120th term
Proceeding in the same way mentioned in (i),
we get upper quartile = 164 [Point Z]
Interquartile range = Q3-Q1
= 164-152
= 12
(iii)Mark a point O(172 ) on X axis. Draw a line parallel to Y axis from O.
Let it meet the curve at N. Draw a straight line from N to Y axis which meets at M.
M = 144
Hence number of students whose height is more than 172 cm is 160-144 = 16
14. 100 pupils in a school have heights as tabulated below
| Height in cm | 121-130 | 131-140 | 141-150 | 151-160 | 161-170 | 171-180 |
| No. of pupils | 12 | 16 | 30 | 20 | 14 | 8 |
Draw the ogive for the above data and from it determine the median (use graph paper).
Solution:
We write the given data in cumulative frequency table (in continuous distribution):
| Height | No. of students | Cumulative frequency c.f |
| 120.5-130.5 | 12 | 12 |
| 130.5-140.5 | 16 | 28 |
| 140.5-150.5 | 30 | 58 |
| 150.5-160.5 | 20 | 78 |
| 160.5-170.5 | 14 | 92 |
| 170.5-180.5 | 8 | 100 |
Plot the points (130.5, 12), (140.5, 28), (150.5, 58), (160.5, 78), (170.5, 92) and (180.5, 100) on the graph.
Join the points with the free hand. We get an ogive as shown:
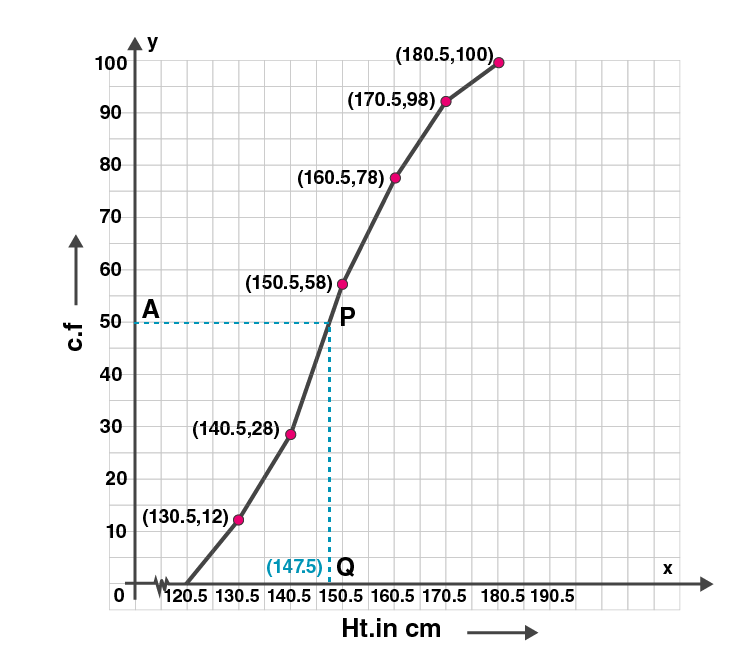
Here n = 100
Median = (n/2)th term
= 100/2
= 50th term
Mark point A(50) on Y axis. Draw a line parallel to X axis from A.
Let it meet the curve at P. Draw a straight line from P to X axis which meets at Q.
Q = 147.5
Hence median is 147.5.
Chapter Test
1. Arun scored 36 marks in English, 44 marks in Civics, 75 marks in Mathematics and x marks in Science. If he has scored an average of 50 marks, find x.
Solution:
Marks scored in English = 36
Marks scored in Civics = 44
Marks scored in Mathematics = 75
Marks scored in Science = x
No. of subjects = 4
Average marks = sum of marks / No. of subjects = 50 [Given]
(36+44+75+x)/4 = 50
155+x = 4×50
155+x = 200
x = 200-155
x = 45
Hence the value of x is 45.
2. The mean of 20 numbers is 18. If 3 is added to each of the first ten numbers, find the mean of new set of 20 numbers.
Solution:
Given the mean of 20 numbers = 18
Sum of numbers = 18×20 = 360
If 3 is added to each of first 10 numbers, then new sum = (3×10)+360
= 30+360
= 390
New mean = 390/20
= 19.5
Hence the mean of new set of 20 numbers is 19.5.
3. The average height of 30 students is 150 cm. It was detected later that one value of 165 cm was wrongly copied as 135 cm for computation of mean. Find the correct mean.
Solution:
Average height of 30 students = 150 cm
So sum of height = 150×30 = 4500
Difference between correct value and wrong value = 165-135 = 30
So actual sum = 4500+30 = 4530
So actual mean = 4530/30 = 31
Hence the correct mean 31.
4. There are 50 students in a class of which 40 are boys and the rest girls. The average weight of the students in the class is 44 kg and average weight of the girls is 40 kg. Find the average weight of boys.
Solution:
Total number of students = 50
No. of boys = 40
No. of girls = 50-40 = 10
Average weight of 50 students = 44 kg
So sum of weight = 44×50 = 2200 kg
Average weight of girls = 40 kg
So sum of weight of girls = 40×10 = 400 kg
Total weight of boys = 2200-400 = 1800 kg
Average weight of boys = 1800/40 = 45 kg
Hence the average weight of boys is 45 kg.
5. The contents of 50 boxes of matches were counted giving the following results.
| No. of matches | 41 | 42 | 43 | 44 | 45 | 46 |
| No. of boxes | 5 | 8 | 13 | 12 | 7 | 5 |
Calculate the mean number of matches per box.
Solution:
| No. o f matches x | No. of boxes f | fx |
| 41 | 5 | 205 |
| 42 | 8 | 336 |
| 43 | 13 | 559 |
| 44 | 12 | 528 |
| 45 | 7 | 315 |
| 46 | 5 | 230 |
| Total | Ʃf = 50 | Ʃfx =2173 |
Mean = Ʃfx/Ʃf
= 2173/50
= 43.46
Hence the mean is 43.46.
6. The heights of 50 children were measured (correct to the nearest cm) giving the following results
| Height (in cm) | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 |
| No. of children | 1 | 4 | 5 | 7 | 11 | 10 | 6 | 4 | 2 |
Calculate the mean height for this distribution correct to one place of decimal.
Solution:
| Height x | No. of children f | fx |
| 65 | 1 | 65 |
| 66 | 4 | 264 |
| 67 | 5 | 335 |
| 68 | 7 | 476 |
| 69 | 11 | 759 |
| 70 | 10 | 700 |
| 71 | 6 | 426 |
| 72 | 4 | 288 |
| 73 | 2 | 146 |
| Total | Ʃf = 50 | Ʃfx = 3459 |
Mean = Ʃfx/Ʃf
= 3459/50
= 69.18
= 69.2 [corrected to one decimal place]
Hence the mean is 69.2.
7. Find the value of p for the following distribution whose mean is 20.6.
| Variate (xi) | 10 | 15 | 20 | 25 | 35 |
| Frequency (fi) | 3 | 10 | p | 7 | 5 |
Solution:
| Variate (xi) | Frequency (fi) | fx |
| 10 | 3 | 30 |
| 15 | 10 | 150 |
| 20 | p | 20p |
| 25 | 7 | 175 |
| 35 | 5 | 175 |
| Total | Ʃfi = 25+p | Ʃfi xi = 530+20p |
Mean = Ʃfx/Ʃf
20.6 = (530+20p )/(25+p) [Given mean = 20.6]
20.6(25+p) = (530+20p)
515 + 20.6p = 530+20p
20.6p-20p = 530-515
0.6p = 15
p = 15/0.6
p = 25
Hence the value of p is 25.
8. Find the value of p if the mean of the following distribution is 18.
| Variate (xi) | 13 | 15 | 17 | 19 | 20+p | 23 |
| Frequency (fi) | 8 | 2 | 3 | 4 | 5p | 6 |
Solution:
| Variate (xi) | Frequency (fi) | fi xi |
| 13 | 8 | 104 |
| 15 | 2 | 30 |
| 17 | 3 | 51 |
| 19 | 4 | 76 |
| 20+p | 5p | 5p2+100p |
| 23 | 6 | 138 |
| Total | Ʃfi = 23+5p | Ʃfi xi = 399+5p2+100p |
Mean = Ʃfi xi / Ʃfi
18 = (399+5p2+100p)/( 23+5p) [Given mean = 18]
18(23+5p) = 399+5p2+100p
414 + 90p = 399+5p2+100p
5p2+100p-90p+399-414 = 0
5p2+10p-15 = 0
Dividing by 5, we get
p2+2p-3 = 0
(p-1)(p+3) = 0
p-1 = 0 or p+3 = 0
p = 1 or p = -3
p cannot be negative.
So p = 1
Hence the value of p is 1.
9. Find the mean age in years from the frequency distribution given below:
| Age in years | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 |
| No. of persons | 4 | 14 | 22 | 16 | 6 | 5 | 3 |
Solution:
The given distribution is not continuous.
Adjustment factor = (30-29)/2 = ½ = 0.5
We subtract 0.5 from lower limit of the class interval and add 0.5 to upper limit.
So the new table in continuous form is given below.
| Age | Mid value xi | No. of persons fi | fixi |
| 24.5-29.5 | 27 | 4 | 108 |
| 29.5-34.5 | 32 | 14 | 448 |
| 34.5-39.5 | 37 | 22 | 814 |
| 39.5-44.5 | 42 | 16 | 672 |
| 44.5-49.5 | 47 | 6 | 282 |
| 49.5-54.5 | 52 | 5 | 260 |
| 54.5-59.5 | 57 | 3 | 171 |
| Total | Ʃfi = 70 | Ʃ fixi = 2755 |
Mean = Ʃfi xi / Ʃfi
= 2755/70
= 39.357
= 39.36
Hence the mean age is 39.36 years.
10. Calculate the Arithmetic mean, correct to one decimal place, for the following frequency
| Marks | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| Students | 2 | 4 | 5 | 16 | 20 | 10 | 6 | 8 | 4 |
Solution:
Class mark, xi = (upper class limit + lower class limit)/2
| Marks | Students fi | Class mark xi | fixi |
| 10-20 | 2 | 15 | 30 |
| 20-30 | 4 | 25 | 100 |
| 30-40 | 5 | 35 | 175 |
| 40-50 | 16 | 45 | 720 |
| 50-60 | 20 | 55 | 1100 |
| 60-70 | 10 | 65 | 650 |
| 70-80 | 6 | 75 | 450 |
| 80-90 | 8 | 85 | 680 |
| 90-100 | 4 | 95 | 380 |
| Total | Ʃfi = 75 | Ʃfixi = 4285 |
Mean = Ʃfi xi / Ʃfi
= 4285/75
= 57.133
= 57.1
Hence the mean is 57.1.
11. The mean of the following frequency distribution is 62.8. Find the value of p.
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 | 100-120 |
| Frequency | 5 | 8 | p | 12 | 7 | 8 |
Solution:
| Class | Frequency fi | Class mark xi | fixi |
| 0-20 | 5 | 10 | 50 |
| 20-40 | 8 | 30 | 240 |
| 40-60 | p | 50 | 50p |
| 60-80 | 12 | 70 | 840 |
| 80-100 | 7 | 90 | 630 |
| 100-120 | 8 | 110 | 880 |
| Total | Ʃfi = 40+p | Ʃfixi = 2640+50p |
Mean = Ʃfi xi / Ʃfi
62.8 = (2640+50p)/( 40+p) [Given mean = 62.8]
62.8(40+p) = 2640+50p
2512+62.8p = 2640+50p
62.8p-50p = 2640-2512
12.8p = 128
p = 128/12.8
p = 10
Hence the value of p is 10.
12. The daily expenditure of 100 families are given below. Calculate f1, and f2, if the mean daily expenditure is Rs 188.
| Expenditure in Rs | 140-160 | 160-180 | 180-200 | 200-220 | 220-240 |
| No. of families | 5 | 25 | f1 | f2 | 5 |
Solution:
Given mean = 188
| Class | Frequency fi | Class mark xi | fixi |
| 140-160 | 5 | 150 | 750 |
| 160-180 | 25 | 170 | 4250 |
| 180-200 | f1 | 190 | 190f1 |
| 200-220 | f2 | 210 | 210f2 |
| 220-240 | 5 | 230 | 1150 |
| Total | Ʃfi = 35+f1+f2 = 100 | Ʃfixi = 6150+190f1+210f2 |
Given no. of families = 100
So 35+f1+f2 = 100
f1+f2 = 100-35 = 65
f1 = 65-f2 ..(i)
Mean = Ʃfi xi / Ʃfi
188 = (6150+190f1+210f2)/100 [Given mean = 188]
188(100) = 6150+190f1+210f2
18800 = 6150+190f1+210f2
18800-6150 = 190f1+210f2
12650 = 190f1+210f2 ..(ii)
Substitute (i) in (ii)
12650 = 190(65-f2)+210f2
12650 = 12350-190f2+210f2
12650-12350 = -190f2+210f2
300 = 20f2
f2 = 300/20 = 15
Put f2 in (i)
f1 = 65-15
f1 = 50
Hence the value of f1 and f2 is 50 and 15 respectively.
13. The measures of the diameter of the heads of 150 screw is given in the following table. If the mean diameter of the heads of the screws is 51.2 mm, find the values of p and q .
| Diameter in mm | 32-36 | 37-41 | 42-46 | 47-51 | 52-56 | 57-61 | 62-66 |
| No. of screws | 15 | 17 | p | 25 | q | 20 | 30 |
Solution:
Given mean = 51.2 mm
The given distribution is not continuous.
Adjustment factor = (37-36)/2 = ½ = 0.5
We subtract 0.5 from lower limit of the class interval and add 0.5 to upper limit.
So the new table in continuous form is given below.
| Diameter in mm | Mid value xi | No. of screws fi | fixi |
| 31.5-36.5 | 34 | 15 | 510 |
| 36.5-41.5 | 39 | 17 | 663 |
| 41.5-46.5 | 44 | p | 44p |
| 46.5-51.5 | 49 | 25 | 1225 |
| 51.5-56.5 | 54 | q | 54q |
| 56.5-61.5 | 59 | 20 | 1180 |
| 61.5-66.5 | 64 | 30 | 1920 |
| Total | Ʃfi = 107+p+q | Ʃ fixi = 5498+44p+54q |
Given No. of screws = 150
107+p+q = 150
p = 150-107-q
p = 43-q ..(i)
Mean = Ʃfi xi / Ʃfi
51.2 = (5498+44p+54q)/150
51.2×150 = 5498+44p+54q
7680 = 5498+44(43-q)+54q
7680 = 5498+1892-44q+54q
7680 -5498-1892 = -44q+54q
290 = 10q
q = 290/10 = 29
Put q in (i)
p = 43-29
p = 14
Hence the value of p and q is 14 and 29 respectively.
14. The median of the following numbers, arranged in ascending order is 25. Find x.
11, 13, 15, 19, x + 2, x + 4, 30, 35, 39, 46
Solution:
Here n = 10, which is even
Median = 25
So Median = ½ ( n/2 th term + ((n/2)+1)th term)
25 = ½ (( 10/2 )th term + (10/2)+1)th term)
25 = ½ (( 5 )th term + (6)th term)
25 = ½ (x+2 + x+4)
25 = ½ (2x+6)
2x+6 = 25×2
2x+6 = 50
2x = 50-6 = 44
x = 44/2 = 22
Hence the value of x is 22.
15. If the median of 5, 9, 11, 3, 4, x, 8 is 6, find the value of x.
Solution:
Arranging numbers in ascending order
3,4,5,x,8,9,11
Here n = 7 which is odd
Given median = 6
So Median =( (n+1)/2) th term
6 = ((7+1)/2)th term
6 = ((8/2)th term
6 = 4th term
6 = x
Hence the value of x is 6.
16. Find the median of: 17, 26, 60, 45, 33, 32, 29, 34, 56 .
If 26 is replaced by 62, find the new median.
Solution:
Arranging numbers in ascending order
17,26,29,32,33,34,45,56,60
Here n = 9 which is odd.
So Median =( (n+1)/2) th term
Median = ((9+1)/2)th term
Median = (10/2)th term
Median = 5th term
Median = 33
Hence median is 33.
If 26 is replaced by 62, new set of numbers in ascending order is shown below.
17,29,32,33,34,45,56,60,62
Here n = 9 which is odd.
So Median =( (n+1)/2) th term
Median = ((9+1)/2)th term
Median = (10/2)th term
Median = 5th term
Median = 34
Hence median is 34.
17. The marks scored by 16 students in a class test are : 3, 6, 8, 13, 15, 5, 21, 23, 17, 10, 9, 1, 20, 21, 18, 12
Find
(i) the median
(ii) lower quartile
(iii) upper quartile
Solution:
Arranging data in ascending order
1,3,5,6,8,9,10,12,13,15,17,18,20,21,21,23
Here n = 16 which is even
(i) So median = ½ ( n/2 th term + ((n/2)+1)th term)
= ½ (16/2 th term + ((16/2)+1)th term)
= ½ (8 th term + (8+1)th term)
= ½ (8 th term + 9th term)
= ½ (12+13)
= ½ ×25
= 12.5
Hence the median is 12.5.
(ii) Lower quartile, Q1 = (n/4) th term
= (16)/4
= 4 th term
= 6
Hence the lower quartile is 6.
(iii)Upper quartile, Q3 = (3n/4) th term
= (3×16/4) th term
= (3×4)th term
= 12 th term
= 18
Hence the upper quartile is 18.
18. Find the median and mode for the set of numbers : 2, 2, 3, 5, 5, 5, 6, 8, 9
Solution:
Here n = 9 which is odd.
Median = ((n+1)/2)th term
Median = ((9+1)/2)th term
Median = (10/2)th term
Median = 5 th term
Median = 5
Mode is the number which appears most often in a set of numbers.
Here 5 occurs maximum number of times.
So mode is 5.
19. Calculate the mean, the median and the mode of the following distribution.
| Age in years | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| No. of students | 2 | 3 | 5 | 6 | 4 | 3 | 2 |
Solution:
| Age in years xi | No. of students fi | Cumulative frequency | fixi |
| 12 | 2 | 2 | 24 |
| 13 | 3 | 5 | 39 |
| 14 | 5 | 10 | 70 |
| 15 | 6 | 16 | 90 |
| 16 | 4 | 20 | 64 |
| 17 | 3 | 23 | 51 |
| 18 | 2 | 25 | 36 |
| Total | Ʃfi = 25 | Ʃ fixi = 374 |
Mean = Ʃ fixi/ Ʃfi
= 374/25
= 14.96
Hence the mean is 14.96.
Here n = 25 which is odd.
Median = ((n+1)/2)th term
Median = ((25+1)/2)th term
Median = (26/2)th term
Median = 13 th term
Median = 15
Hence the median is 15.
Here 15 occurs maximum number of times. i.e., 6 times.
Hence the mode is 15.
20. The daily wages of 30 employees in an establishment are distributed as follows:
| Daily wages in Rs | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| No. of employees | 1 | 8 | 10 | 5 | 4 | 2 |
Estimate the modal daily wages for this distribution by a graphical method.
Solution:
| Daily wages in Rs. | No. of employees |
| 0-10 | 1 |
| 10-20 | 8 |
| 20-30 | 10 |
| 30-40 | 5 |
| 40-50 | 4 |
| 50-60 | 2 |
Taking daily wages on x-axis and No. of employees on the y-axis and draw a histogram as shown below.

Join AB and CD intersecting each other at M. From M draw ML perpendicular to x-axis.
L is the mode
Here Mode = Rs 23
Hence the mode is Rs. 23.
21. Using the data given below, construct the cumulative frequency table and draw the ogive.
From the ogive, estimate :
(i) the median
(ii) the inter quartile range.
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Frequency | 3 | 8 | 12 | 14 | 10 | 6 | 5 | 2 |
Also state the median class
Solution:
Arranging the data in cumulative frequency table.
| Marks | Frequency | Cumulative frequency |
| 0-10 | 3 | 3 |
| 10-20 | 8 | 11 |
| 20-30 | 12 | 23 |
| 30-40 | 14 | 37 |
| 40-50 | 10 | 47 |
| 50-60 | 6 | 53 |
| 60-70 | 5 | 58 |
| 70-80 | 2 | 60 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis).
Plot the points (10, 3), (20, 11), (30, 23), (40, 37), (50, 47), (60, 53), (70, 58) and (80, 60) on the graph.
Join the points with the free hand. We get an ogive as shown:
(i)Here number of observations, n = 60 which is even.
So median = ( n/2) th term
= (60/2) th term
= 30 th term
Mark a point A(30) on Y-axis. From A, draw a horizontal line parallel to X-axis meeting the curve at P. From P draw a line perpendicular to the x-axis which meets it at Q.
Q is the median .
Q = 35
Hence the median is 35 .
(ii) Lower quartile, Q1 = n/4 = 60/4 = 15th term
Upper quartile, Q3 = 3n/4 = 3×60/4 = 45th term
Mark a point B(15) and C(45) on Y-axis. From B and C, draw a horizontal line parallel to X-axis meeting the curve at L and M respectively. From L and M, draw lines perpendicular to the x-axis which meets it at E and F respectively.
E is the lower quartile .
E = 22.3
F is the upper quartile.
F = 47
Inter quartile range = Q3-Q1
= 47-22.3
= 24.7
Hence interquartile range is 24.7.
22. Draw a cumulative frequency curve for the following data :
| Marks obtained | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| No. of students | 8 | 10 | 22 | 40 | 20 |
Hence determine:
(i) the median
(ii) the pass marks if 85% of the students pass.
(iii) the marks which 45% of the students exceed.
Solution:
Arranging the data in cumulative frequency table.
| Marks obtained | No. of students f | Cumulative frequency |
| 0-10 | 8 | 8 |
| 10-20 | 10 | 18 |
| 20-30 | 22 | 40 |
| 30-40 | 40 | 80 |
| 40-50 | 20 | 100 |
To represent the data in the table graphically, we mark the upper limits of the class intervals on
the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis ( y-axis).
Plot the points (10, 8), (20, 18), (30, 40), (40, 80), and(50,100) on the graph.
Join the points with the free hand. We get an ogive as shown:
(i) Here number of observations, n = 100 which is even.
So median = ( n/2) th term
= (100/2) th term
= 50 th term
Mark a point A(50) on Y-axis. From A, draw a horizontal line parallel to X-axis meeting the curve at P. From P, draw a line perpendicular to the x-axis which meets it at Q.
Q is the median .
Q = 32.5
Hence the median is 32.5 .
(ii)Total number of students = 100
85% of 100 = 85
Remaining number of students = 100-85 = 15
Mark a point B(15) on Y axis. From B, draw a horizontal line parallel to X-axis meeting the curve at L. From L, draw a line perpendicular to the x-axis which meets it at M.
Here M = 18
The pass marks will be 18 if 85% of students passed.
(iii) Total number of students = 100
45% of 100 = 45
Remaining number of students = 100-45 = 55
Mark a point C(55) on Y axis. From C, draw a horizontal line parallel to X-axis meeting the curve at E. From E, draw a line perpendicular to the x-axis which meets it at F.
Here F = 34
Hence marks which 45% of students exceeds is 34 marks.
Download PDF
ML Aggarwal Solutions for Class 10 Maths Chapter 21- Measures Of Central Tendency
Download PDF: ML Aggarwal Solutions for Class 10 Maths Chapter 21- Measures Of Central Tendency PDF
Chapterwise ML Aggarwal Solutions for Class 10 Maths :
- Chapter 1- Goods and Service Tax (GST)
- Chapter 2- Banking
- Chapter 3- Shares and Dividends
- Chapter 4- Linear Inequations
- Chapter 5- Quadratic Equations in One Variable
- Chapter 6- Factorization
- Chapter 7- Ratio and Proportion
- Chapter 8- Matrices
- Chapter 9- Arithmetic and Geometric Progression
- Chapter 10- Reflection
- Chapter 11- Section Formula
- Chapter 12- Equation of Straight Line
- Chapter 13- Similarity
- Chapter 14- Locus
- Chapter 15- Circles
- Chapter 16- Constructions
- Chapter 17- Mensuration
- Chapter 18- Trigonometric Identities
- Chapter 19- Trigonometric Tables
- Chapter 20- Heights and Distances
- Chapter 21- Measures Of Central Tendency
- Chapter 22- Probability
About ML Aggarwal
M. L. Aggarwal, is an Indian mechanical engineer, educator. His achievements include research in solutions of industrial problems related to fatigue design. Recipient Best Paper award, Manipal Institute of Technology, 2004. Member of TSTE.
