Maharashtra Board Solutions Class 9-Maths (Part 2): Chapter 3.3- Triangles

Class 9: Maths Chapter 3.3 solutions. Complete Class 9 Maths Chapter 3.3 Notes.

Maharashtra Board Solutions Class 9-Maths (Part 2): Chapter 3.3- Triangles

Maharashtra Board 9th Maths Chapter 3.3, Class 9 Maths Chapter 3.3 solutions

Question 1.
Find the values of x and y using the information shown in the given figure. Find the measures of ∠ABD and ∠ACD.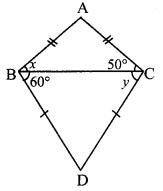

Solution:
i. ∠ACB = 50° [Given]
In ∆ABC, seg AC ≅ seg AB [Given]
∴ ∠ABC ≅ ∠ACB [Isosceles triangle theorem]
∴ x = 50°

ii. ∠DBC = 60° [Given]
In ABDC, seg BD ≅ seg DC [Given]
∴ ∠DCB ≅ ∠DBC [Isosceles triangle theorem]
∴ y = 60°

iii. ∠ABD = ∠ABC + ∠DBC [Angle addition property]
= 50° + 60°
∴ ∠ABD = 110°

iv. ∠ACD = ∠ACB + ∠DCB [Angle addition property]
= 50° + 60°
∴ ∠ACD = 110°
∴ x = 50°, y = 60°,
∠ABD = 110°, ∠ACD = 110°

Question 2.
The length of hypotenuse of a right angled triangle is 15. Find the length of median on its hypotenuse.

Solution:
Length of hypotenuse = 15 [Given]
Length of median on the hypotenuse = 12 x length of hypotenuse [In a right angled triangle, the length of the median on the hypotenuse is half the length of the hypotenuse]
= 12 x 15 = 7.5
∴ The length of the median on the hypotenuse is 7.5 units.

Question 3.
In ∆PQR, ∠Q = 90°, PQ = 12, QR = 5 and QS is a median. Find l(QS).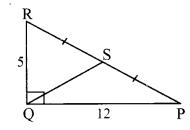

Solution:
i. PQ = 12, QR = 5 [Given]
In APQR, ∠Q = 90° [Given]
∴ PR² = QR² + PQ² [Pythagoras theorem]
= 25 + 144
∴ PR² =169
∴ PR = 13 units [Taking square root of both sides]

ii. In right angled APQR, seg QS is the median on hypotenuse PR.
∴ QS = 12PR [In a right angled triangle, the length of the median on the hypotenuse is half the length of the hypotenuse]
= 12 x 13
∴ l(QS) = 6.5 units

Question 4.
In the given figure, point G is the point of concurrence of the medians of ∆PQR. If GT = 2.5, find the lengths of PG and PT.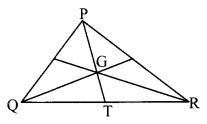

Solution:
i. In ∆PQR, G is the point of concurrence of the medians. [Given]
The centroid divides each median in the ratio 2 : 1.
PG : GT = 2 : 1

∴ PG = 2 x 2.5
∴ PG = 5 units

ii. Now, PT = PG + GT [P – G – T]
= 5 + 2.5
∴ l(PG) = 5 units, l(PT) = 7.5 units

Question 1.
Can the theorem of isosceles triangle be proved by doing a different construction? (Textbook pg. no.34)

Solution:
Yes
Construction: Draw seg AD ⊥ seg BC.
Proof:
In ∆ABD and ∆ACD,
seg AB≅ seg AC [Given]
∠ADB ≅ ∠ADC [Each angle is of measure 90°]
seg AD ≅ seg AD [Common side]
∴ ∆ABD ≅ ∆ACD [Hypotenuse side test]
∴ ∠ABD ≅ ∠ACD [c.a.c.t.]
∴ ∠ABC ≅ ∠ACB [B-D-C]

Question 2.
Can the theorem of isosceles triangle be proved without doing any construction? (Textbook pg, no.34)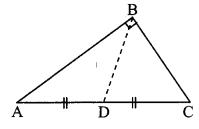

Solution:
Yes
Proof:
In ∆ABC and ∆ACB,
seg AB ≅ seg AC [Given]
∠BAC ≅ ∠CAB [Common angle]
seg AC ≅ seg AB [Given]
∴ ∆ABC ≅ ∆ACB [SAS test]
∴ ∠ABC ≅ ∠ACB [c. a. c. t.]

Question 3.
In the given figure, ∆ABC is a right angled triangle, seg BD is the median on hypotenuse. Measure the lengths of the following segments.
i. AD
ii. DC
iii. BD
From the measurements verify that BD = 12AC. (Textbook pg. no. 37)
Solution:
AD = DC = BD= 1.9 cm
AC = AD + DC [A – D – C]
= 1.9 + 1.9
= 2 x 1.9 cm
∴ AC = 2 x BD
∴ BD = 12 AC

Download PDF

Maharashtra Board Solutions Class 9-Maths (Part 2): Chapter 3.3- Triangles

Download PDF: Maharashtra Board Solutions Class 9-Maths (Part 2): Chapter 3.3- Triangles PDF

Chapterwise Maharashtra Board Solutions Class 9 Maths :

Part 2

• Chapter 1.1- Basic Concepts in Geometry
• Chapter 1.2- Basic Concepts in Geometry
• Chapter 1.3- Basic Concepts in Geometry
• Chapter 2.1- Parallel Lines
• Chapter 2.2- Parallel Lines
• Chapter 3.1- Triangles
• Chapter 3.2- Triangles
• Chapter 3.3- Triangles
• Chapter 3.4- Triangles
• Chapter 3.5- Triangles
• Chapter 4.1- Constructions of Triangles
• Chapter 4.2- Constructions of Triangles
• Chapter 4.3- Constructions of Triangles
• Chapter 5.1- Quadrilaterals
• Chapter 5.2- Quadrilaterals
• Chapter 5.3- Quadrilaterals
• Chapter 5.4- Quadrilaterals
• Chapter 5.5- Quadrilaterals
• Chapter 6.1- Circle
• Chapter 6.2- Circle
• Chapter 6.3- Circle
• Chapter 7.1- Co-ordinate Geometry
• Chapter 7.2- Co-ordinate Geometry
• Chapter 8.1- Trigonometry
• Chapter 8.2- Trigonometry
• Chapter 9.1- Surface Area and Volume
• Chapter 9.2- Surface Area and Volume
• Chapter 9.3- Surface Area and Volume

FAQs

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC. 

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.