NCERT Solutions for Class 9, Maths Chapter 15

Class 9: Maths Chapter 15 solutions. Complete Class 9 Maths Chapter 15 Notes.

Contents

1 NCERT Solutions for 9th class Maths : Chapter 15 Probability
2 NCERT Solutions for 9th class Maths : Chapter 15: Download PDF
3 Chapterwise NCERT Solutions for Class 9 Maths :
4 About NCERT

NCERT Solutions for 9th class Maths : Chapter 15 Probability

NCERT 9th Maths Chapter 15, class 9 Maths Chapter 15 solutions

Page No: 283

Exercise 15.1

1. In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.

Answer

Total numbers of balls = 30
Numbers of boundary = 6
Numbers of time she didn’t hit boundary = 30 – 6 = 24
Probability she did not hit a boundary = 24/30 = 4/5

2. 1500 families with 2 children were selected randomly, and the following data were recorded:

Number of girls in a family	2	1	0
Number of families	475	814	211

Compute the probability of a family, chosen at random, having
(i) 2 girls (ii) 1 girl (iii) No girl
Also check whether the sum of these probabilities is 1.

Answer

Total numbers of families = 1500

(i) Numbers of families having 2 girls = 475
Probability = Numbers of families having 2 girls/Total numbers of families
= 475/1500 = 19/60
(ii) Numbers of families having 1 girls = 814
Probability = Numbers of families having 1 girls/Total numbers of families
= 814/1500 = 407/750
(iii) Numbers of families having 2 girls = 211
Probability = Numbers of families having 0 girls/Total numbers of families
= 211/1500
Sum of the probability = 19/60 + 407/750 + 211/1500
= (475 + 814 + 211)/1500 = 1500/1500 = 1
Yes, the sum of these probabilities is 1.

3. Refer to Example 5, Section 14.4, Chapter 14. Find the probability that a student of the class was born in August.

Answer

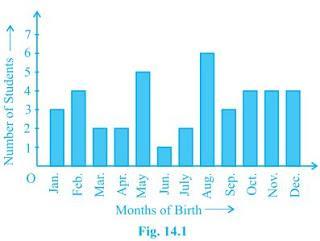
NCERT Solutions for 9th class Maths : Chapter 15 Probability Ex. 15.1 Que. 3

Total numbers of students = 40
Numbers of students = 6
Required probability = 6/40 = 3/20

4. Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes:

Outcome	3 heads	2 heads	1 head	No head
Frequency	23	72	77	28

If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.

Answer

Number of times 2 heads come up = 72
Total number of times the coins were tossed = 200
Required probability = 72/200 = 9/25

5. An organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:

Monthly income (in ₹)	Vehicles per family
0	1	2	Above 2
Less than 7000	10	160	25	0
7000-10000	0	305	27	2
10000-13000	1	535	29	1
13000-16000	2	469	59	25
16000 or more	1	579	82	88

Suppose a family is chosen. Find the probability that the family chosen is

(i) earning ₹10000 – 13000 per month and owning exactly 2 vehicles.
(ii) earning ₹16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than ₹7000 per month and does not own any vehicle.
(iv) earning ₹13000 – 16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.

Answer

Total numbers of families = 2400

(i) Numbers of families earning ₹10000 –13000 per month and owning exactly 2 vehicles = 29
Required probability = 29/2400

(ii) Number of families earning ₹16000 or more per month and owning exactly 1 vehicle = 579
Required probability = 579/2400

(iii) Number of families earning less than ₹7000 per month and does not own any vehicle = 10 Required probability = 10/2400 = 1/240

(iv) Number of families earning ₹13000-16000 per month and owning more than 2 vehicles = 25
Required probability = 25/2400 = 1/96

(v) Number of families owning not more than 1 vehicle = 10+160+0+305+1+535+2+469+1+579

= 2062

Required probability = 2062/2400 = 1031/1200

Page No: 284

NCERT 9th Maths Chapter 15, class 9 Maths Chapter 15 solutions

6. Refer to Table 14.7, Chapter 14.
(i) Find the probability that a student obtained less than 20% in the mathematics test.
(ii) Find the probability that a student obtained marks 60 or above.

Marks	Number of students
0 – 20	7
20 – 30	10
30 – 40	10
40 – 50	20
50 – 60	20
60 – 70	15
70 – above	8
Total	90

Answer

Total numbers of students = 90

(i) Numbers of students obtained less than 20% in the mathematics test = 7
Required probability = 7/90

(ii) Numbers of student obtained marks 60 or above = 15+8 = 23
Required probability = 23/90

7. To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table.

Opinion	Number of students
like	135
dislike	65

Find the probability that a student chosen at random
(i) likes statistics, (ii) does not like it.

Answer

Total numbers of students = 135 + 65 = 200

(i) Numbers of students who like statistics = 135
Required probability = 135/200 = 27/40

(ii) Numbers of students who does not like statistics = 65
Required probability = 65/200 = 13/40

8. Refer to Q.2, Exercise 14.2. What is the empirical probability that an engineer lives:
(i) less than 7 km from her place of work?
(ii) more than or equal to 7 km from her place of work?
(iii) within 1/2 km from her place of work?

Answer

The distance (in km) of 40 engineers from their residence to their place of work were found as follows:
5 3 10 20 25 11 13 7 12 31 19 10 12 17 18 11 3 2 17 16 2 7 9 7 8 3 5 12 15 18 3 12 14 2 9 6 15 15 7 6 12

Total numbers of engineers = 40
(i) Numbers of engineers living less than 7 km from her place of work = 9
Required probability = 9/40

(ii) Numbers of engineers living less than 7 km from her place of work = 40 – 9 = 31
Required probability = 31/40

(iii) Numbers of engineers living less than 7 km from her place of work = 0
Required probability = 0/40 = 0

Page No: 285

11. Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg):
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.

Answer

Total numbers of bags = 11
Numbers of bags containing more than 5 kg of flour = 7
Required probability = 7/11

12. In Q.5, Exercise 14.2, you were asked to prepare a frequency distribution table, regarding the concentration of sulphur dioxide in the air in parts per million of a certain city for 30 days. Using this table, find the probability of the concentration of sulphur dioxide in the interval 0.12-0.16 on any of these days.
The data obtained for 30 days is as follows:
0.03 0.08 0.08 0.09 0.04 0.17 0.16 0.05 0.02 0.06 0.18 0.20 0.11 0.08 0.12 0.13 0.22 0.07 0.08 0.01 0.10 0.06 0.09 0.18 0.11 0.07 0.05 0.07 0.01 0.04

Answer

Total numbers of days data recorded = 30 days
Numbers of days in which sulphur dioxide in the interval 0.12-0.16 = 2
Required probability = 2/30 = 1/15

13. In Q.1, Exercise 14.2, you were asked to prepare a frequency distribution table regarding the blood groups of 30 students of a class. Use this table to determine the probability that a student of this class, selected at random, has blood group AB.
The blood groups of 30 students of Class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.

Answer

Total numbers of students = 30
Numbers of students having blood group AB = 3
Required probability = 3/30 = 1/10

Chapter 15 Probability Class 9 Maths NCERT Solutions is good way through which one can build their basic knowledge. The numerical measure of uncertainty of an activity is called probability. The words ‘doubt’, ‘chances’, ‘most probably’ etc., show uncertainty or probability of happening of an action or activity.

• Probability – an Experimental Approach: A trial is an action which results in one or several outcomes. An event for an experiment is the collection of some outcomes of the experiment. Let n be the total number of trials. The empirical probability P(E) of an event E happening, is given by

P(E) = Number of trials in which the event happened/The total number of trials.

Only one exercise is present in the chapter 15 NCERT Solutions. We have also provided exercise wise solutions of every problem that you can find below.

You will get accurate and detailed NCERT Solutions of Class 9 Maths prepared by Indcareer Schools experts that can help in easily understand even the most difficult problems. You will be able to solve the difficult problems given in a exercise.

NCERT Solutions for Class 9 Maths Chapters:

FAQ on Chapter 15 Probability

What are the benefits of NCERT Solutions for Chapter 15 Probability Class 9 NCERT Solutions?

Chapter 15 Probability NCERT Solutions that are very helpful in building your basic concepts embedded in the chapter. It is also very helpful in developing your problem solving skills.

What do you mean by random experiment?

An experiment in which all possible outcomes are known and the exact outcome cannot be predicted in advance, is called a random experiment.

What is uncertainty in Probability?

A doubtful situation of an action or activity that may or may not take place, is called ‘uncertainty’.

A coin is thrown once. Find the probability of getting a head.

Number of possible outcomes = 2

Number of favourable outcome = 1

∴ The required probability = (1/2).

NCERT 9th Maths Chapter 15, class 9 Maths Chapter 15 solutions

NCERT Solutions for 9th class Maths : Chapter 15: Download PDF

NCERT Solutions for 9th class Maths : Chapter 15 Probability

Download PDF: NCERT Solutions for 9th class Maths : Chapter 15 Probability PDF

Chapterwise NCERT Solutions for Class 9 Maths :

About NCERT

The National Council of Educational Research and Training is an autonomous organization of the Government of India which was established in 1961 as a literary, scientific, and charitable Society under the Societies Registration Act. Its headquarters are located at Sri Aurbindo Marg in New Delhi. Visit the Official NCERT website to learn more.

NCERT Solutions

NCERT Solutions for Class 9

NCERT Solutions for Class 9 Maths