NCERT Exemplar Class 8 Maths Chapter 10: Direct and Inverse Proportions. NCERT Exemplar Solutions for Class 8 Maths Chapter 10 Direct and Inverse Proportions prepare students for their Class 8 exams thoroughly.
Maths problems and solutions for the Class 8 pdf are provided here which are similar to the questions being asked in the previous year’s board.
Contents
NCERT Exemplar Class 8 Maths Chapter 10: Direct and Inverse Proportions
Class 8: Maths Chapter 10 solutions. Complete Class 8 Maths Chapter 10 Notes.
Main Concepts and Results
- Two quantities x and y are said to be in direct proportion if they increase or decrease together in such a manner that the ratio oftheir corresponding values remains constant. That is, x y = k where k is a positive number, if x and y are in direct proportion or vary directly. In case of direct proportion, if y1, y2 are the values of y corresponding to the values x1, x2 of x respectively, then
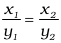
- Two quantities x and y are said to be in inverse proportion if an increase in x causes a proportional decrease in y and vice-versa, in such a manner that the product of their corresponding values remains constant. That is, xy = k where k is a positive number, if x and y are in inverse proportion. In this case, if y1, y2 are the values of y corresponding to the values x1, x2 of x respectively, then x1 y1= x2 y2 or
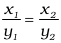
- Quantities increasing or decreasing together need not always be in direct proportion, same in the case of inverse proportion.
- When two quantities x and y are in direct proportion (or vary directly), they are written as x ∝ y. Symbol “∝” stands for ‘is proportional to’.
- When two quantities x and y are in inverse proportion (or vary inversely) they are written as x ∝ 1 /y .
Solved Examples
In examples 1 to 3, there are four options out of which one is correct.
Choose the correct answer,


In examples 4 to 6, fill in the blanks to make the statements true.

In examples 7 to 9, state whether the statements are true (T) or false (F):






Think and Discuss
1. What will happen if question is: If 30 men can reap a field in 17 days, then 10 men reap the field in how many days?
2. In the questions of men and work we always use indirect variation. Now think of some situation related to men where direct variation will be used, e.g. If maximum 15 men can travel by three cars, then find minimum maximum number of cars required for (a) 25 men (b) 38 men.
Multiple Choice Questions

Fill in the Blanks Type Questions

True False Type Questions

Short Answer Type Questions

Application, Games and Puzzles
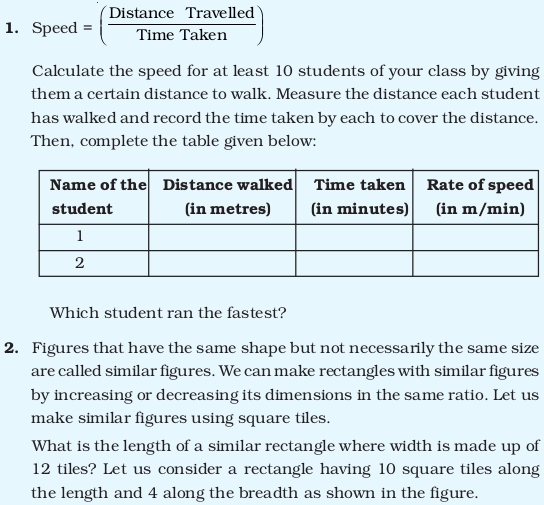

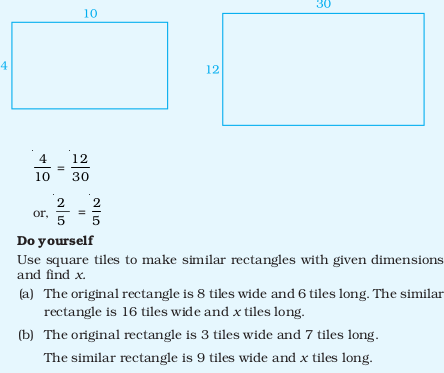

Answers to Multiple Choice Questions





