NCERT Exemplar Class 12 Maths Chapter 8: Application of Integrals. NCERT Exemplar Solutions for Class 12 Maths Chapter 8 Application of Integrals prepare students for their Class 12 exams thoroughly.
Maths problems and solutions for the Class 12 pdf are provided here which are similar to the questions being asked in the previous year’s board.
NCERT Exemplar Class 12 Maths Chapter 8: Application of Integrals
Class 12: Maths Chapter 8 solutions. Complete Class 12 Maths Chapter 8 Notes.
Overview
This chapter deals with a specific application of integrals to find the area under simple curves, area between lines and arcs of circles, parabolas and ellipses, and finding the area bounded by the above said curves.
1. The area of the region bounded by the curve y = f (x), x-axis and the lines x = a and x = b (b > a) is given by the formula:

2. The area of the region bounded by the curve x = Φ (y), y-axis and the lines y = c, y = d is given by the formula:

3. The area of the region enclosed between two curves y = f (x), y = g (x) and the lines x = a, x = b is given by the formula.
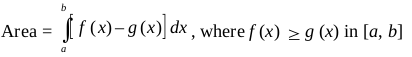
4 If f (x) ≥ g (x) in [a, c] and f (x) ≤ g (x) in [c, b], a < c < b, then

Short Answer Type Questions (Solved Examples)
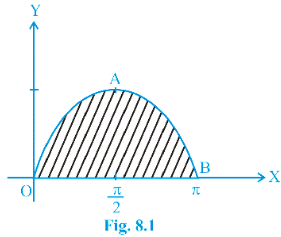
Example 1 Find the area of the curve y = sin x between 0 and π.
Solution We have

Example 2 Find the area of the region bounded by the curve ay² = x³ , the y-axis and
the lines y = a and y = 2a.
Solution We have
Click here to download the NCERT Exemplar Class 12 Maths Unit 8 Application of Integrals.

Example 3 Find the area of the region bounded by the parabola y 2 = 2x and the straight line x – y = 4.
Solution The intersecting points of the given curves are obtained by solving the equations x – y = 4 and y² = 2x for x and y. We have y² = 8 + 2y i.e., (y – 4) (y + 2) = 0 which gives y = 4, –2 and x = 8, 2.
Thus, the points of intersection are (8, 4), (2, –2). Hence
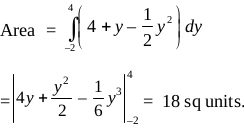

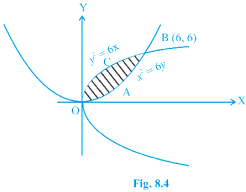
Example 4 Find the area of the region bounded by the parabolas y² = 6x and x² = 6y.
Solution The intersecting points of the given parabolas are obtained by solving these equations for x and y, which are 0(0, 0) and (6, 6). Hence
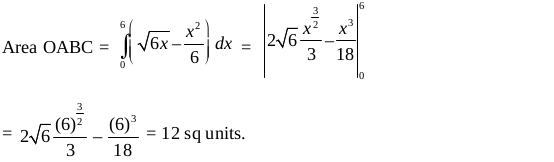
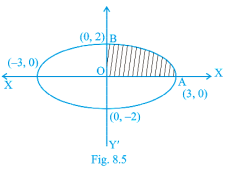
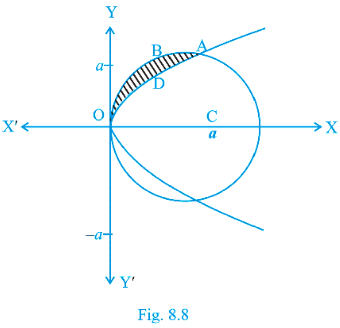
Example 5 Find the area enclosed by the curve x = 3 cost, y = 2 sint.
Solution Eliminating t as follows:

Long Answer Type Questions (Solved Examples)
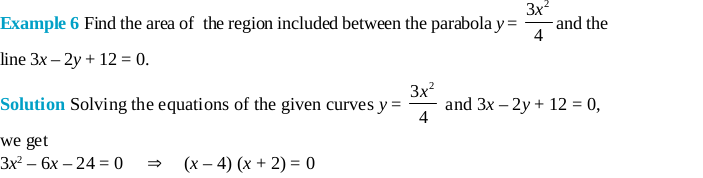

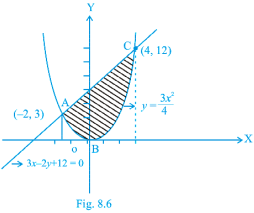
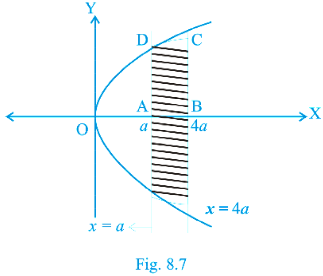
Example 7 Find the area of the region bounded by the curves x = at² and y = 2 at between the ordinate
coresponding to t = 1 and t = 2.
Solution Given that x = at² …(i),
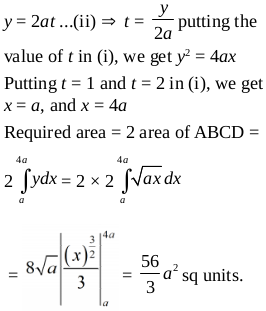

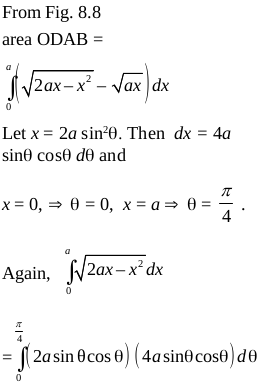
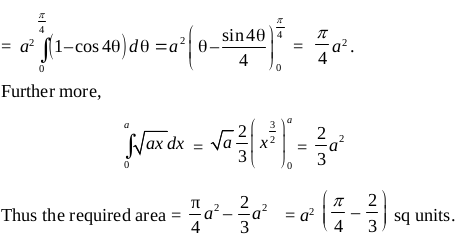
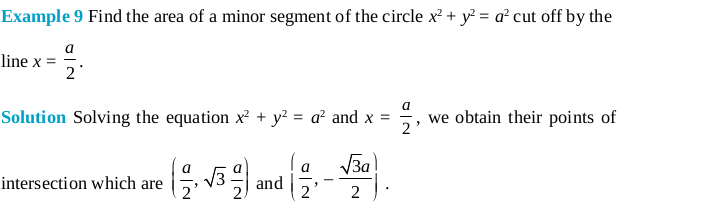



Objective Type Questions (Solved Examples)
Choose the correct answer from the given four options in each of the Examples 10 to 12.


Short Answer Type Questions

Long Answer Type Questions

Multiple Choice Questions

Answers