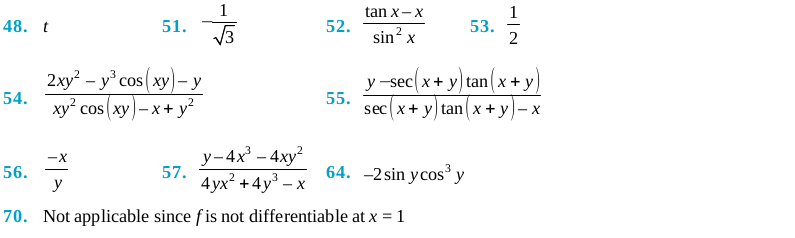NCERT Exemplar Class 12 Maths Chapter 5: Continuity and Differentiability

NCERT Exemplar Class 12 Maths Chapter 5: Continuity and Differentiability. NCERT Exemplar Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability prepare students for their Class 12 exams thoroughly.

Maths problems and solutions for the Class 12 pdf are provided here which are similar to the questions being asked in the previous year's board.

NCERT Exemplar Class 12 Maths Chapter 5: Continuity and Differentiability

Class 12: Maths Chapter 5 solutions. Complete Class 12 Maths Chapter 5 Notes.

5.1 Overview
5.1.1 Continuity of a function at a point
Let f be a real function on a subset of the real numbers and let c be a point in the domain of f. Then f is continuous at c if

More elaborately, if the left hand limit, right hand limit and the value of the function at x = c exist and are equal to each other, i.e.,

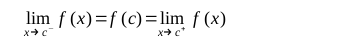
then f is said to be continuous at x = c.

5.1.2 Continuity in an interval

(i) f is said to be continuous in an open interval (a, b) if it is continuous at every point in this interval.
(ii) f is said to be continuous in the closed interval [a, b] if

5.1.3 Geometrical meaning of continuity

(i) Function f will be continuous at x = c if there is no break in the graph of the function at the point (c,f(c)).
(ii) In an interval, function is said to be continuous if there is no break in the graph of the function in the entire interval.

5.1.4 Discontinuity

The function f will be discontinuous at x = a in any of the following cases :

5.1.5 Continuity of some of the common functions

5.1.6 Continuity of composite functions

Let f and g be real valued functions such that (fog) is defined at a. If g is continuous at a and f is continuous at g (a), then (fog) is continuous at a.

5.1.7 Differentiability

5.1.8 Algebra of derivatives

If u, v are functions of x, then

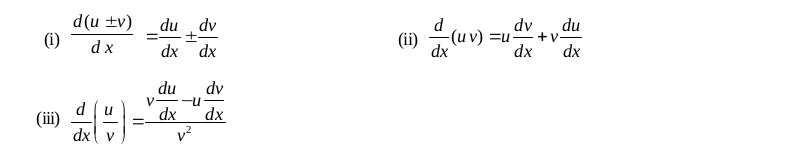
5.1.9 Chain rule is a rule to differentiate composition of functions. Let f = vou. If

5.1.10 Following are some of the standard derivatives (in appropriate domains)

Click Here to download NCERT Exemplar Class 12 Maths Unit 5 Continuity and Differentiability.

5.1.11 Exponential and logarithmic functions

(i) The exponential function with positive base b > 1 is the function y = f (x) = b^x . Its domain is R, the set of all real numbers and range is the set of all positive real numbers. Exponential function with base 10 is called the common exponential function and with base e is called the natural exponential function.
(ii) Let b > 1 be a real number. Then we say logarithm of a to base b is x if b^x =a, Logarithm of a to the base b is denoted by log_b a. If the base b = 10, we say it is common logarithm and if b = e, then we say it is natural logarithms. logx denotes the logarithm function to base e. The domain of logarithm function is R⁺ , the set of all positive real numbers and the range is the set of all real numbers.
(iii) The properties of logarithmic function to any base b > 1 are listed below:

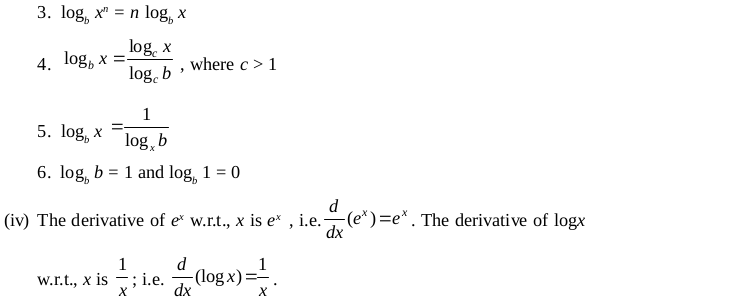
5.1.12 Logarithmic differentiation is a powerful technique to differentiate functions of the form f (x) = (u (x)) ^v(x) , where both f and u need to be positive functions for this technique to make sense.

5.1.13 Differentiation of a function with respect to another function

Let u = f (x) and v = g (x) be two functions of x, then to find derivative of f (x) w.r.t. to g (x), i.e., to find
du/dv , we use the formula

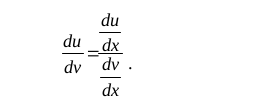
5.1.14 Second order derivative

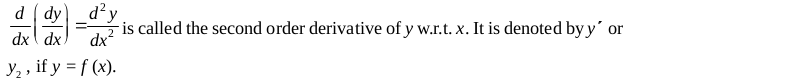
5.1.15 Rolle’s Theorem

Let f : [a, b] → R be continuous on [a, b] and differentiable on (a, b), such that f (a) = f (b), where a and b are some real numbers. Then there exists at least one point c in (a, b) such that f ′ (c) = 0.
Geometrically Rolle’s theorem ensures that there is at least one point on the curve y = f (x) at which tangent is parallel to x-axis (abscissa of the point lying in (a, b)).

5.1.16 Mean Value Theorem (Lagrange)

Let f : [a, b] → R be a continuous function on [a, b] and differentiable on (a, b). Then there exists at least one point c in (a, b) such that

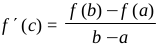
Geometrically, Mean Value Theorem states that there exists at least one point c in (a, b) such that the tangent at the point (c, f (c)) is parallel to the secant joining the points (a, f (a) and (b, f (b)).

Short Answer Type Questions (Solved Examples)

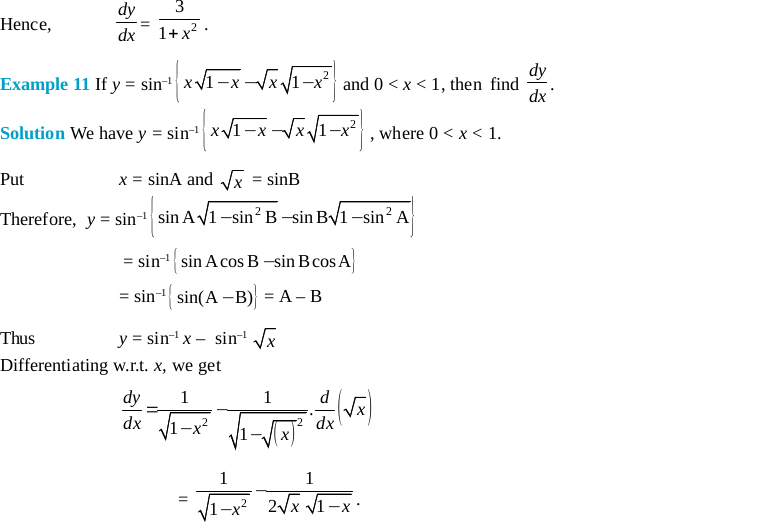
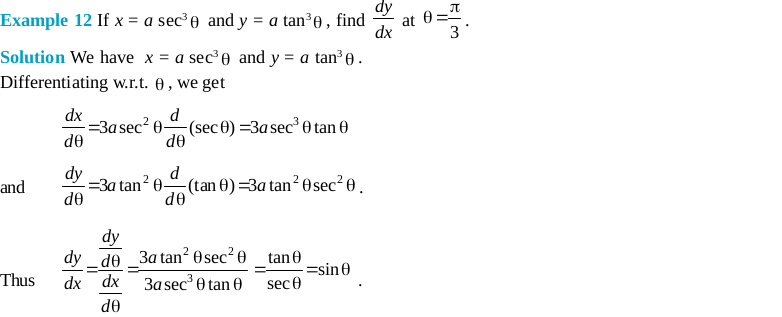
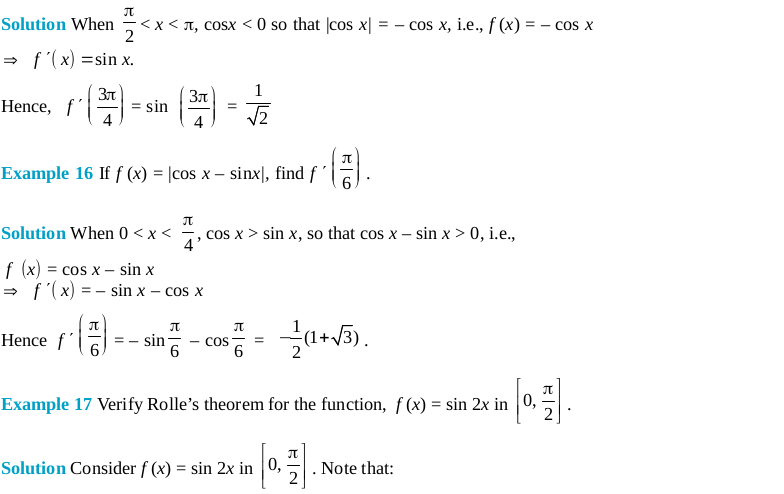
Long Answer Type Questions (Solved Examples)

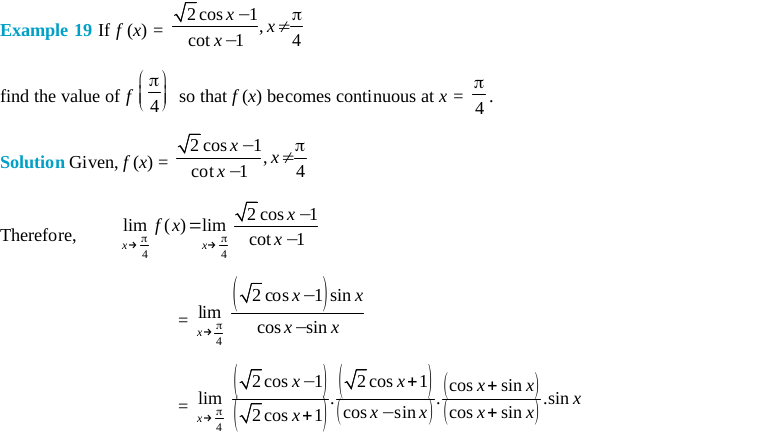
Click Here to download NCERT Exemplar Class 12 Maths Unit 5 Continuity and Differentiability.

Objective Type Questions (Solved Examples)

Match the Following (Solved Example)

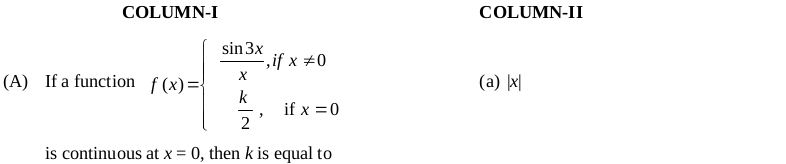
Fill in the Blanks (Solved Examples)

True or False Statements Type Questions (Solved Examples)

Short Answer Type Questions (Exercise)

Click Here to download NCERT Exemplar Class 12 Maths Unit 5 Continuity and Differentiability.

Long Answer Type Questions (Exercise)

Multiple Choice Questions

Fill In Blanks Type Questions

True or False Statements Type Questions

Answers