Contents
- 1 अतिलघु उत्तरीय प्रश्न (VERY SHORT ANSWER TYPE QUESTIONS)
- 2 Question 1
- 3 Question 2
- 4 Question 3
- 5 Question 4
- 6 लघु उत्तरीय प्रश्न (SHORT ANSWER TYPE QUESTIONS)
- 7 Question 5
- 8 Question 6
- 9 Question 7
- 10 Question 8
- 11 Question 9
- 12 Question 10
- 13 Question 11
- 14 Question 12
- 15 Question 13
- 16 Question 14
- 17 Question 15
- 18 Question 16
- 19 Question 17
- 20 Question 18
- 21 Question 19
- 22 Question 20
- 23 Question 21
- 24 Question 22
- 25 Question 23
- 26 Question 24
- 27 Question 25
- 28 Question 26
- 29 Question 27
- 30 Question 28
- 31 Question 29
- 32 Question 30
- 33 Question 31
- 34 Question 32
- 35 Question 33
- 36 Question 34
- 37 Question 35
- 38 Question 36
- 39 Question 37
- 40 Question 38
- 41 Question 39
- 42 Question 40
- 43 Question 41
- 44 Question 42
- 45 Question 43
- 46 Question 44
- 47 Question 45
- 48 Question 46
- 49 Question 47
- 50 Question 48
- 51 Question 49
- 52 Question 50
अतिलघु उत्तरीय प्रश्न (VERY SHORT ANSWER TYPE QUESTIONS)
Question 1
ΔABC में ∠A=90°, AB=12 cm और AC=4√3 cm, तब ∠B , ज्ञात करें।
Sol :
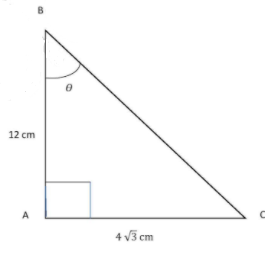
माना ∠B=θ
$\tan \theta=\frac{A C}{A B}=\frac{4 \sqrt{3}}{12}=\frac{\sqrt{3}}{3}$
$=\frac{\sqrt{3}}{\sqrt{3} \times \sqrt{3}}=\frac{1}{\sqrt{3}}$
tan θ=tan 30°
θ=30°
∠B=θ=30°
Question 2
एक उदग्र स्तम्भ 7√3 m ऊँचा है और इसकी छाया की लम्बाई 21 m है । प्रकाश स्रोत का उन्नयन कोण ज्ञात करें।
Sol :
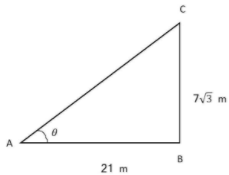
स्तम्भ 7√3 m ऊँचा है और छाया की लम्बाई 21 m है ।
माना प्रकाश स्त्रोत का उन्नयन कोण θ है ।
$\tan \theta=\frac{P}{B}=\frac{\mathrm{BC}}{\mathrm{AC}}$
$\tan \theta=\frac{7 \sqrt{3}}{213}=\frac{\sqrt{3}}{3 \sqrt{3}}=\frac{1}{\sqrt{3}}$
tan θ=tan 30°
θ=30°
θ=30°
∴उन्नयन कोण=θ=30°
Question 3
30 m लम्बी सीढ़ी एक दिवाल पर इस प्रकार लगी है कि उसका शिरा 15 m ऊंची दिवाल के शिखर पर पहुँचती है । सीढ़ी जमीन के साथ कितना कोण बनाती है ।
Sol :

माना कि BC सीढ़ी की लम्बांई=30 m है तथा AB=15 m दिवाल की ऊँचाई है तथा जमीन के साथ बना कोण=θ
$\sin \theta=\frac{P}{H}=\frac{\mathrm{AB}}{\mathrm{BC}}$
$\sin \theta=\frac{15}{30}$
$\sin \theta=\frac{1}{2}$
Sin θ=Sin 30°
θ=30°
∴जमीन के साथ बना कोण=θ=30°
Question 4
जब टेलीफोन स्तम्भ की ऊँचाई और उसकी छाया की लम्बाई का अनुपात √3 : 1 है, तो सूर्य का उन्नयन कोण ज्ञात करें।
Sol :
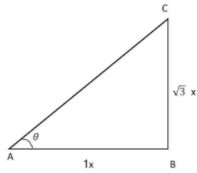
माना उन्नयन कोण=θ
दिया है:
स्तम्भ की ऊँचाई : छाया की लम्बाई का अनुपात √3 : 1
माना सामान्य अंतर x है।
$\dfrac{BC}{AB}=\dfrac{√3x}{1x}$
$\tan \theta=\frac{Perpendicular}{Base}=\frac{\mathrm{BC}}{\mathrm{AB}}$
$\tan \theta=\frac{\sqrt{3}x}{1x}=\sqrt{3}$
tan θ=tan 60°
θ=60°
∴उन्नयन कोण=θ=60°
लघु उत्तरीय प्रश्न (SHORT ANSWER TYPE QUESTIONS)
Question 5
ΔABC एक समकोण त्रिभुज है जिसमें AB=8 m, ∠BCA=30° , तब ज्ञात करें:
(i) C से A का उन्नयन कोण।
(ii) A से C का अवनयन कोण।
(iii) BC और AB
Sol :

(i) ΔABC
AB=8 m, ∠BCA=30°
C से A का उन्नयन कोण=30°
(ii) ∵उन्नयान=अवनयन कोण
∠BCA=∠BAC
30°=∠BAC
∴A से C का अवनयन=30°
(iii) ΔABC
AB=8 cm (दिया है),
∠C=30°
$\tan \theta=\frac{P}{B}$
$\tan 30^{\circ}=\frac{8}{BC}$
$\frac{1}{\sqrt{3}}=\frac{8}{BC}$
BC=8√3 m
Question 6
ΔABC एक समकोण त्रिभुज है जिसमें BC क्षैतिज है, AB=8 m, ∠BAC=60° तब ज्ञात करे:
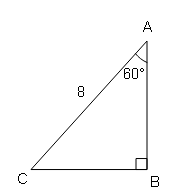
(i) C से A का उन्नयन कोण।
Sol :
एक त्रिभुज के तीनो कोणों का योग 180° होता है।
∠BAC+∠CBA+∠BCA=180°
90°+60°+∠BCA=180°
150°+∠BCA=180°
∠BCA=180°-150°=30°
(ii) A से C का अवनयन कोण।
Sol :

DA समानांतर CB , AC तिर्यक रेखा
∠DAC=∠BCA (एकांतर अन्तः कोण)
∠DAC=30°
(iii) C से B की दूरी।
Sol :
tan θ$=\frac{P}{B}$
$\tan 30^{\circ}=\frac{8}{CB}$
$\frac{1}{\sqrt{3}}=\frac{8}{CB}$
BC=8√3
Question 7
चित्र में PQR एक समकोण त्रिभुज है जिसमें QR=8√3 m और ∠QPR=30°. QP ज्ञात करें ।

Sol :
$\tan \theta=\frac{P}{B}$
$\tan 30^{\circ}=\frac{8\sqrt{3}}{QP}$
$\frac{1}{\sqrt{3}}=\frac{8\sqrt{3}}{QP}$
QP=8√3×3
QP=24 m
Question 8
समकोण ΔABC में कर्ण AC=12 cm और ∠A=60°, तब शेष भुजाओं की लम्बाइयाँ ज्ञात करें।

Sol :
$\sin 60^{\circ}=\frac{BC}{AC}$
$\frac{\sqrt{3}}{2}=\frac{BC}{12}$
BC=6√3
$\cos 60^{\circ}=\frac{AB}{AC}$
$\frac{1}{2}=\frac{AB}{12}$
AB=6 cm
∴शेष भुजाओं की लम्बाइयाँ AB=6 cm , BC=6√3
Question 9
समकोण ΔABC में AC कर्ण है। AB=12 cm और ∠BAC=30° तब BC भुजा की लम्बाई ज्ञात करें।

Sol :
$\tan 30^{\circ}=\frac{BC}{AB}$
$\frac{1}{\sqrt{3}}=\frac{BC}{12}$
$BC=\frac{12}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
$BC=\frac{12\sqrt{3}}{3}$
BC=4√3
Question 10
क्षैतिज तल पर स्थित एक बिन्दु से एक मीनार का उन्नयन कोण 45° है। यदि बिन्दु की दूरी मीनार से 20 m हो तो मीनार की ऊँचाई ज्ञात करें ।
Sol :

tan θ$=\frac{P}{B}$
$\tan 45^{\circ}=\frac{AB}{BC}$
$1=\frac{AB}{20}$
AB=20 m
Question 11
AB एक उदग्र दिवाल है और B जमीन पर है। एक सीढ़ी AC का सिरा C जमीन पर टिकी है ∠ACB=45°, BC=5 m, तो सीढ़ी की लम्बाई ज्ञात करें।

Sol :
$\cos 45^{\circ}=\frac{BC}{AC}$
$\frac{1}{\sqrt{2}}=\frac{5}{AC}$
AC=5√2 m
∴सीढ़ी की लम्बाई=5√2 m
Question 12
√3 m ऊँचे बाँस के वृक्ष की छाया की लम्बाई 3 m है। छाया के अन्तिम बिन्दु से बाँस के शिखर का उन्नयन कोण क्या होगा ?
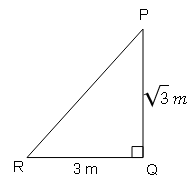
Sol :
tan θ$=\frac{P}{B}$
$\tan \theta=\frac{PQ}{RQ}$
$\tan \theta=\frac{\sqrt{3}}{3}=\frac{\sqrt{3}}{\sqrt{3} \times \sqrt{3}}$
$\tan \theta=\frac{1}{\sqrt{3}}$
tan θ=tan 30°
θ=30°
∴अंतिम बिन्दु से बाँस के शिखर का उन्नयन कोण=30°
Question 13
टेलीफोन के खम्भे की लम्बाई, उसकी छाया की लम्बाई का $\frac{1}{\sqrt{3}}$ गुनी है । तब प्रकाश स्त्रोत का उन्नयन कोण ज्ञात करें।
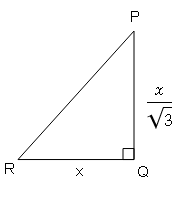
Sol :
माना कि छाया कि लम्बाई RQ=x
तो टेकिफोन के खम्भे की लम्बाई$=\frac{x}{\sqrt{3}}$
प्रकाश स्त्रोत का उन्नयन कोण =∠R=θ
tan θ$=\frac{PQ}{RQ}$
$\tan \theta=\dfrac{\frac{x}{\sqrt{3}}}{x}=\frac{x}{\sqrt{3}}\times \frac{\sqrt{1}}{x}$
$\tan \theta=\frac{1}{\sqrt{3}}$
tan θ=tan 30°
θ=30°
∴प्रकाश स्त्रोत का उन्नयन कोण=30°
Question 14
1.75 m लम्बा प्रेक्षक 25.75 m ऊँची दिवाल से 24 m दूरी पर है | प्रेक्षक की आँख पर दिवाल की चोटी का उन्नयन कोण ज्ञात कीजिए।
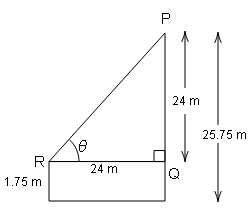
Sol :
माना प्रेक्षक की आँख पर दिवार की चोटी का उन्नयन कोण θ है।
$\tan \theta=\frac{P}{B}=\frac{PQ}{RQ}$
tan θ=1
tan θ=tan 45°
θ=45°
Question 15
एक मीनार जमीन पर उदग्र खड़ा है | मीनार के पद से 15 m दूर एक बिन्दु पर मीनार की चोटी का उन्नमन कोण 60° है| मीनार की ऊँचाई क्या है।
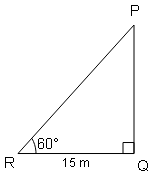
Sol :
tan θ$=\frac{P}{B}=\frac{PQ}{RQ}$
tan 60°$=\frac{PQ}{15}$
$\sqrt{3}=\frac{PQ}{15}$
PQ=15√3 m
मीनार की ऊँचाई=15√3 m
Question 16
एक मीनार के पाद से 20 m दूर स्थित एक बिन्दु से मीनार की चोटी का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।
Sol :

माना मीनार की ऊँचाई PQ है।
tan θ$=\frac{P}{B}=\frac{PQ}{RQ}$
tan 30°$=\frac{PQ}{20}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{20}$
$PQ=\frac{20}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
PQ=11.54 m
∴मीनार की ऊँचाई=11.54 m
Question 17
एक मीनार के जड़ से 50√3 m दूर स्थित एक बिन्दु से मीनार की चोटी का उन्नयन कोण 60° है। मीनार की ऊँचाई ज्ञात कीजिए।
Sol :

माना मीनार की ऊँचाई PQ है।
tan θ$=\frac{PQ}{RQ}$
tan 60°$=\frac{PQ}{50\sqrt{3}}$
$\frac{\sqrt{3}}{1}=\frac{PQ}{50\sqrt{3}}$
PQ=150 m
Question 18
एक सीढ़ी एक उदग्र दिवाल पर इस प्रकार रखा जाता है कि दिवाल की चोटी तक पहुँचता है। सीढ़ी का पाद दिवाल से 1.5 m दूर है और सीढ़ी जमीन से 60° के कोण पर झूका है। दिवाल की ऊँचाई ज्ञात कीजिए ।
Sol :

माना मीनार की ऊँचाई PQ है।
tan θ$=\frac{PQ}{RQ}$
tan 60°$=\frac{PQ}{1.5}$
$\frac{\sqrt{3}}{1}=\frac{PQ}{1.5}$
PQ=1.5√3=1.5×1.73 m
=2.595 m
Question 19
एक पतंग की डोरी 100 m लम्बी है। यदि डोरी एक सरल रेखा में हो और उसमें कोई ढील नहीं हो तथा भुतल सो θ कोण बनाती है इस तरह कि $\sin \theta=\frac{8}{15}$ , तो भुतल से पतंग की ऊँचाई ज्ञात करे।
Sol :
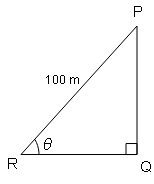
माना मीनार की ऊँचाई PQ है।
sin θ$=\frac{PQ}{RP}$
$\frac{8}{15}=\frac{PQ}{100}$
PQ$=\frac{8\times 100}{15}=\frac{160}{3}$
PQ=53.33 m
Question 20
एक पंतग और धरती पर के एक बिन्दु के बीच डोरी की लम्बाई 85 m है। यदि डोरी जमीन से θ कोण बनाती है इस प्रकार कि $\tan \theta=\frac{15}{8}$, तो पतंग की ऊँचाई बताइए।
Sol :
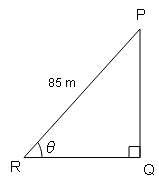
दिया है : $\tan \theta=\frac{15}{8}=\frac{P}{B}$
P=15k , B=8k , H=?
$H=\sqrt{P^2+B^2}$
$H=\sqrt{{15k}^2+{8k}^2}=\sqrt{225k^2+64k^2}$
H=\sqrt{289k^2}=17k
∴17k=85
$k=\frac{85}{17}$
k=5
P=15k=15(5)=75
=75 m
पतंग की ऊँचाई =75 m
Question 21
किसी वृक्ष का ऊपर का भाग जो आँधी से टुट कर पृथ्वी से 30° का कोण बनाता है। वृक्ष की जड़ से उस बिन्दु की दूरी जहाँ वृक्ष का ऊपरी शिरा पृथ्वी को छुता है 25 m है। वृक्ष की प्रारंभिक ऊँचाई ज्ञात कीजिए।
Sol :
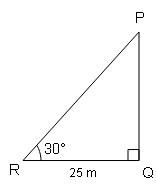
tan θ$=\frac{P}{B}$
tan 30°$=\frac{PQ}{25}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{25}$
PQ$=\frac{25}{\sqrt{3}}$ m
cos θ$=\frac{B}{H}$
cos 30°$=\frac{25}{PR}$
$\frac{\sqrt{3}}{2}=\frac{25}{PR}$
$PR=\frac{25}{\sqrt{3}}\times 2$
∴प्रारंभिक ऊँचाई =PQ+PR
$=\frac{25}{\sqrt{3}} +\frac{25}{\sqrt{3}}\times 2$
$=\frac{25+50}{\sqrt{3}}=\frac{75}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
$=\frac{75\sqrt{3}}{3}$
=25√3 m
∴वृक्ष की प्रारंभिक ऊँचाई=25√3 m
Question 22
एक बिजली का खम्भा 10 m ऊँचा है । एक स्टील का तार , खम्भे की चोटी से बाँध कर, (इसे सीधा खड़ा रखने के लिए) जमीन पर एक बिन्दु से स्थिर (fix) कर दिया गया है। यदि स्टील तार खम्भें कीं जड़ से जाने वाली क्षैतिज रेखा से 45° का कोण बनाता है, तो स्टील तार की लम्बाई ज्ञात कीजिए।
Sol :

sin θ$=\frac{P}{H}$
sin 45°$=\frac{PQ}{PR}$
$\frac{1}{\sqrt{2}}=\frac{10}{PR}$
PR=10√2 m
स्टील तार की लम्बाई=10√2 m
Question 23
एक नदी को पार करने में एक आदमी को पुल की दिशा में (एक छोर से दूसरे छोर तक) जाने में 250 m दूरी तय करनी पड़ती है। यदि पूल नदी के किनारे के साथ 30° का कोण बनाती है, तब नदी की चौड़ाई ज्ञात कीजिए।
Sol :

माना ABCD एक पुल है। PQ नदी की चौड़ाई है, PR दोनो छोर को बीच की दूरी है तथा पुल एवं किनारे है, तो पुल की चौड़ाई PQ=?
∴ΔPQR में,
PR=250 m, ∠R=30° , PQ=?
sin θ$=\frac{P}{H}=\frac{PQ}{PR}$
sin 30°$=\frac{PQ}{250}$
$\frac{1}{2}=\frac{PQ}{250}$
$PQ=\frac{250}{2}$
PQ=125 m
Question 24
एक वायुयान , जमीन से 30° कोण पर उड़ता हुआ 184 m की दूरी तय करता है। वायुयान जमीन से कितनी ऊपर होगी ।
Sol :
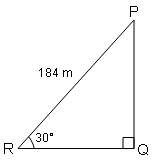
ΔPQR में,
RP=184 m , PQ=?
sin θ$=\frac{P}{H}$
sin 30°$=\frac{PQ}{RP}$
$\frac{1}{2}=\frac{PQ}{184}$
$PQ=\frac{184}{2}$=92 m
∴जमीन से वायुयान की ऊँचाई=92 m
Question 25
1.5 m लम्बा एक आदमी पेड़ की चोटी को देखता है और पाता है कि पेड़ की चोटी उसके आँख पर 60° का उन्नयन कोण बनाता है । यदि पेड़ से आदमी की दूरी 36 m हो, तो पेड़ की ऊँचाई ज्ञात कीजिए।
Sol :
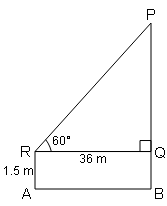
In ΔPQR में,
tan θ$=\frac{P}{B}$
tan 60°$=\frac{PQ}{RQ}$
$\frac{\sqrt{3}}{1}=\frac{PQ}{36}$
PQ=36√3 m
पेड़ की ऊँचाई=(PQ+QB)
=36√3+1.5
=62.352+1.5
=63.852
Question 26
एक आदमी जो $1 \frac{3}{4} \mathrm{~m}$ लम्बा है मन्दिर के चोटी का उन्नयन कोण 30° पाता है यदि आदमी की दूरी मन्दिर से 15 m है, तो मन्दिर की ऊँचाई बताइये।
Sol :
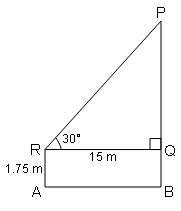
In ΔPQR में,
tan θ$=\frac{P}{B}$
tan 30°$=\frac{PQ}{RQ}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{15}$
PQ$=\frac{15}{\sqrt{3}}$
PQ=5√3
मन्दिर की ऊँचाई=PQ+QB
=5√3+1.75
=8.660+1.75=10.41 m
Question 27
एक ध्वजदंड, एक उदग्र (vertical) मीनार पर खड़ा है । मीनार की जड़ से 10 m दूर स्थित बिन्दु से मीनार एवं ध्वजदंड क्रमशः 45° एवं 15° के कोण बनाते हैं। ध्वजदंड की लम्बाई ज्ञात कीजिए ।
Sol :
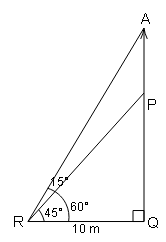
ΔPRQ में,
RQ=10 m , ∠PRQ=45° , PQ=?
tan θ$=\frac{P}{B}$
tan 45°$=\frac{PQ}{RQ}$
$1=\frac{PQ}{10}$
PQ=10 m
ΔARQ में,
RQ=10 m , ∠ARQ=60° , AQ=?
tan θ$=\frac{P}{B}$
tan 60°$=\frac{AQ}{RQ}$
$\frac{\sqrt{3}}{1}=\frac{PQ}{10}$
AQ=10√3 m
∴ध्वजदंड की लम्बाई=AQ-PQ
=10√3-10
=10×1.732-10
=17.32-10
=7.32
Question 28
एक मीनार पर 20 m लम्बा ध्वजदंड खड़ा है । धरती तल पर के एक बिन्दु से ध्वज दंड के पाद और शिखर के उन्नयन कोण क्रमशः 30° और 60° हैं । मीनार की ऊँचाई बताइये ।
Sol :

ΔPRQ में,
tan θ$=\frac{P}{B}$
tan 30°$=\frac{PQ}{RQ}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{RQ}$
$PQ=\frac{RQ}{\sqrt{3}}$…(i)
ΔARQ में,
tan θ$=\frac{P}{B}$
tan 60°$=\frac{AQ}{RQ}$
$\frac{\sqrt{3}}{1}=\frac{AP+PQ}{RQ}$
$\frac{\sqrt{3}}{1}=\frac{20+PQ}{RQ}$ [दिया है: AP=20 m ]
$\frac{\sqrt{3}}{1}=\frac{20+\frac{RQ}{\sqrt{3}}}{RQ}$ [ (i) सें]
$RQ\sqrt{3}=20+\frac{RQ}{\sqrt{3}}$
$RQ\sqrt{3}-\frac{RQ}{\sqrt{3}}=20$
$\frac{RQ\sqrt{3}\times \sqrt{3}-RQ}{\sqrt{3}}=20$
3RQ-RQ=20×√3
2RQ=20√3
$RQ=\frac{20\sqrt{3}}{2}=10\sqrt{3}$
RQ को (i) में रखने पर,
$PQ=\frac{RQ}{\sqrt{3}}$ [(i) से]
$PQ=\frac{10\sqrt{3}}{\sqrt{3}}$
PQ=10 m
मीनार की ऊँचाई PQ=10 m
Question 29
एक मीनार पर एक ध्वजदंड खड़ा है । मीनार के पाद से 60 m कर दूरी पर तल पर के एक बिन्दु से ध्वज दंड के पाद और शिखर के उन्नयन कोण क्रमशः 30° और 60° है । ध्वजदंड की ऊँचाई बताइये।
Sol :

ΔPRQ में,
tan θ$=\frac{P}{B}$
tan 30°$=\frac{PQ}{RQ}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{60}$
$PQ=\frac{60}{\sqrt{3}}$
$PQ=\frac{3\times 20}{\sqrt{3}}=\frac{\sqrt{3}\times \sqrt{3}\times 20}{\sqrt{3}}$
ΔARQ में,
tan θ$=\frac{P}{B}$
tan 60°$=\frac{AQ}{RQ}$
$\sqrt{3}=\frac{AQ}{60}$
AQ=60√3 m
ध्वदजंड की ऊँचाई=AQ-PQ
=60√3-20√3
=√3(60-20)
=40√3 m
Question 30
एक पैंडस्टल के शिखर पर एक 1.46 m ऊँची मूर्ति लगी है । भूमि के एक बिन्दु से मूर्ति के शिखर का उन्नयन कोण 60° है और बिन्दु से पेडस्टल के शिखर का उन्नयन कोण 45° है । पेडस्टल की ऊँचाई ज्ञात करे।
Sol :
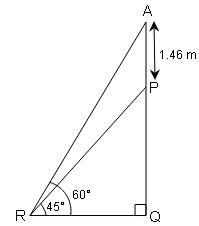
ΔPRQ में,
tan θ$=\frac{P}{B}$
tan 45°$=\frac{PQ}{RQ}$
$1=\frac{PQ}{RQ}$
PQ=RQ..(i)
ΔARQ में,
tan θ$=\frac{P}{B}$
tan 60°$=\frac{AQ}{RQ}$
$\frac{\sqrt{3}}{1}=\frac{AP+PQ}{RQ}$
$\frac{\sqrt{3}}{1}=\frac{1.46+PQ}{RQ}$ [Given : AP=1.46]
$\sqrt{3}=\frac{1.46+PQ}{PQ}$ [From (i)]
$\sqrt{3}=\frac{1.46}{PQ}+\frac{PQ}{PQ}$
$\sqrt{3}=\frac{1.46}{PQ}+1$
$1.732-1=\frac{1.46}{PQ}$
$\frac{0.732}{1}=\frac{1.46}{PQ}$
PQ=$\frac{1.46}{0.732}$
PQ=1.99436
PQ=2 m
पेडस्टल की ऊँचाई ( PQ )=2 m
Question 31
एक मीनार के पाद बिन्दु से एक पहाड़ी का उन्नयन कोण 60° है और पहाड़ी के पाद बिन्दु से मीनार के शिखर का उन्नयन कोण 30° है । यदि मीनार 50 m लम्बी हो, तो पहाड़ी की ऊँचाई क्या होगी ?
Sol :

पहाड़ी की ऊँचाई PQ
पहाड़ी और मीनार के पाद की दूरी RQ
ΔSQR में,
tan 30°$=\frac{50}{RQ}$
$\frac{1}{\sqrt{3}}=\frac{50}{RQ}$
RQ=50√3 m….(i)
ΔPRQ में,
tan 60°$=\frac{PQ}{RQ}$
$\frac{\sqrt{3}}{1}=\frac{PQ}{RQ}$
$\frac{\sqrt{3}}{1}=\frac{PQ}{50\sqrt{3}}$ [from (i)]
PQ=50×3=150 m
∴पहाड़ी की ऊँचाई ( PQ )=150 m
Question 32
(i) एक नदी के किनारे खड़ा एक आदमी देखता है कि दूसरे किनारे पर ठीक उसके सामने खड़े एक वृक्ष का उन्नति कोण 60° है । जब वह आदमी किनारे से 40 m दूर जाता है तो वृक्ष का उन्नति कोण 30° पाता है। वृक्ष की ऊँचाई और नदी की चौड़ाई ज्ञात कीजिए ।
Sol :

वृऋ की ऊँचाई PQ
नदी की चौड़ाई QR
ΔPRQ में,
tan 60°$=\frac{PQ}{QR}$
$\frac{\sqrt{3}}{1}=\frac{PQ}{QR}$
PQ=QR√3…(i)
ΔPSQ में,
$\frac{1}{\sqrt{3}}=\frac{PQ}{QR+RS}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{QR+40}$ [Given: RS=40 m]
$\frac{QR+40}{\sqrt{3}}=PQ$….(ii)
From (i) and (ii),
QR+40=QR×√3×√3
QR+40=3QR
40=3QR-QR
2QR=40
$QR=\frac{40}{2}$
QR=20 m
∴नदी की चौड़ाई ( QR )=20 m
PQ=QR√3 [From (i)]
PQ=20√3
∴वृऋ की ऊँचाई ( PQ )=20√3 m
(ii) एक नदी के किनारे पर एक टाँवर लम्बवत् खड़ा है। टावर के ठीक सामने दूसरे किनारे पर के अन्य बिन्दु से टावर के शिखर का उन्नयन कोण 60° है। किनारे पर इस बिन्दु से 30 मीटर दूर और इस बिन्दु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्दु से टावर के शिखर का उन्नयन कोण 30° है। टावर की ऊँचाई और नदी की चौडाई ज्ञात करें।
Sol :

टावर की ऊँचाई ( PQ )
नदी की चौडाई ( QR )
ΔPRQ में,
tan 60°$=\frac{PQ}{QR}$
$\frac{\sqrt{3}}{1}=\frac{PQ}{QR}$
PQ=QR√3…(i)
ΔPSQ में,
tan 30°$=\frac{PQ}{QS}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{QR+RS}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{QR+30}$ [Given: RS=30 m]
$\frac{QR+30}{\sqrt{3}}=PQ$….(ii)
From (i) and (ii),
QR+30=QR×√3×√3
QR+30=3QR
30=3QR-QR
2QR=30
$QR=\frac{30}{2}$
QR=15 m
∴नदी की चौड़ाई ( QR )=15 m
PQ=QR√3 [From (i)]
PQ=15√3
∴वृऋ की ऊँचाई ( PQ )=15√3 m
Question 33
(i) एक मीनार पर 10 m ऊँचा ध्वजदण्ड खड़ा है । धरती की सतह पर के एक बिन्दु से ध्वज-दण्ड के शिखर और पाद के उन्नयन कोण क्रमश: 60° और 30° है, तो मीनार की ऊँचाई ज्ञात करें ।
Sol :

मीनार की ऊँचाई ( SQ )
मीनार के पाद से धरती पर स्थित बिन्दु की दूरी ( QR )
ΔPQR में,
tan 30°$=\frac{PQ}{QR}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{QR}$
PQ√3=QR….(i)
ΔPSQR में,
tan 60°$=\frac{SQ}{QR}$
$\frac{\sqrt{3}}{1}=\frac{SP+PQ}{QR}$
$\frac{\sqrt{3}}{1}=\frac{10+PQ}{QR}$ [Given : SP=10 m]
$\frac{\sqrt{3}}{1}=\frac{10+PQ}{PQ\sqrt{3}}$ [From (i)]
PQ×√3×√3=10+PQ
3PQ=10+PQ
3PQ-PQ=10
2PQ=10
$PQ=\frac{10}{2}=5$
मीनार की ऊँचाई ( PQ )=5 m
(ii) एक ध्वज-दण्ड एक मीनार पर खड़ा है । मीनार के आधार से d दूरी पर ध्वज दण्ड के शिखर एवं मीनार के शिखर के उन्नयन कोण क्रमशः β और ⍺ हैं। सिद्ध कीजिए कि ध्वजदण्ड की उँचाई d(tan β-tan ⍺) है ।
Sol :

ध्वजदंड की उँचाई ( AP )
मीनार की उँचाई ( PQ )
ΔPQR में,
tan ⍺$=\frac{PQ}{QR}$
$\tan \alpha=\frac{PQ}{d}$ [Given : QR=d]
PQ=d tan ⍺ ….(i)
ΔARQ में,
tan β$=\frac{AQ}{QR}$
$\tan \beta=\frac{AQ}{d}$
AQ=d tan β ….(ii)
AP+PQ=d tan β [From (i)]
AP+(d tan ⍺)=d tan β
AP=d tan β-d tan ⍺
AP=d(tan β-tan ⍺)
ध्वजदंड की उँचाई ( AP )=d(tan β-tan ⍺)
(iii) एक उदग्र मीनार क्षैतिज तल पर खड़ा है और इसके शिखर पर h ऊँचाई का एक ध्वजदण्ड है । क्षैतिज तल पर के एक बिन्दु पर ध्वजदण्ड के पाद एवं शिखर के उन्नयन कोण क्रमशः ⍺ और β हैं। सिद्ध कीजिए कि मीनार की ऊँचाई $\frac{h \tan \alpha}{\tan \beta-\tan \alpha}$
Sol :

मीनार की ऊँचाई ( PQ )
मीनार के पाद से भूमी के बिन्दु के बीच की दूरी ( RQ )
ΔPQR में,
tan ⍺$=\frac{PQ}{RQ}$…(i)
PQ=RQ tan ⍺ ….(ii)
ΔARQ में,
tan β$=\frac{AQ}{RQ}$
tan β$=\frac{AP+PQ}{RQ}$
tan β$=\frac{h+PQ}{RQ}$ [Given: AP=h]
tan β$=\frac{h}{RQ}+\frac{PQ}{RQ}$
tan β$=\frac{h}{RQ}+\tan \alpha$ [From (i)]
tan β-tan ⍺$=\frac{h}{RQ}$
RQ$=\frac{h}{\tan \beta-\tan \alpha}$
[From (ii)]
मीनार की ऊँचाई ( PQ )=RQ tan ⍺
$=\frac{h}{\tan \beta-\tan \alpha}\times \tan \alpha$
$=\frac{h \tan \alpha}{\tan \beta-\tan \alpha}$
Question 34
क्षैतिज तल के किसी बिन्दु से चर्च स्पात्रा के किसी बिन्दु का उन्नयन कोण 45° है । चर्च की तरफ 30 m जाने पर उन्नयन कोण 60° हो जाता है । चर्च स्पात्रा की ऊँचाई ज्ञात कीजिए ।
Sol :
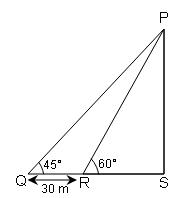
चर्च स्पात्रा की ऊँचाई ( PS )
30 m चर्च की ओर जाने पर अब वह चर्च से RS दूरी पर है।
ΔPSR में,
tan 60°$=\frac{PS}{RS}$
$\frac{\sqrt{3}}{1}=\frac{PS}{RS}$
PS=RS√3…(i)
tan 45°$=\frac{PS}{QS}$
$1=\frac{PS}{QR+RS}$
$1=\frac{PS}{30+RS}$ [Given : QR=30 m]
30+RS=PS
30+RS=RS√3 [From (i)]
30=RS√3-RS
30=RS(√3-1)
$RS=\frac{30}{\sqrt{3}-1}$
∴चर्च स्पात्रा की ऊँचाई ( PS )
PS=RS√3
PS$=\frac{30}{\sqrt{3}-1} \times \sqrt{3}$
PS$=\frac{30\sqrt{3}}{\sqrt{3}-1} \times \frac{\sqrt{3}+1}{\sqrt{3}+1}$
PS$=\frac{30\sqrt{3}(\sqrt{3}+1)}{(\sqrt{3})^2-(1)^2}$
$PS=\frac{30\times 3+30\sqrt{3}}{3-1}=\frac{90+30\sqrt{3}}{2}$
PS=70.98 m
Question 35
(i) एक हेलीकोप्टर पायलट 1000 m की ऊँचाई से अपने बाँयें और दाँये एक ही ऊँचाई पर उड़ते हुए दो वायुयानों को देखता है, जिनके अवनमन कोण क्रमशः 45° और 60° हैं। दोनों वायुयानों के बीच की दूरी ज्ञात करें ।
Sol :
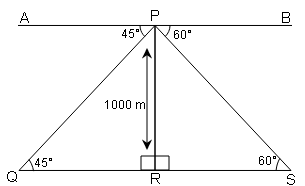
दोनों वायुयानों के बीच की दूरी ( QS )
∠APQ=∠PQR=45° (alternate interior angle)
∠BPS=∠PSR (alternate interior angle)
tan 45°$=\frac{PR}{QR}$
$1=\frac{PR}{QR}$
$1=\frac{1000}{QR}$ [Given: PR=1000 m]
QR=1000 m
tan 60°$=\frac{PR}{RS}$
$\frac{\sqrt{3}}{1}=\frac{1000}{RS}$ [Given : PR=1000 m]
$RS=\frac{1000}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
$RS=\frac{1000\sqrt{3}}{3}$
$RS=\frac{1732}{3}$
दोनों वायुयानों के बीच की दूरी ( QS )
=QR+RS
$=1000+\frac{1732}{3}$
=1000+577.332
=1000+577.332
=1577.332 m
=1577.4 m
(ii) समुद्र तल से 100 m ऊँचे लाइट-हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण क्रमशः 30° और 45° हैं । यदि लाइट हाउस के एक ही और एक जहाज दूसरे जहाज के ठीक पीछे हो, तो दोनों जहाजों के बीच की दूरी ज्ञात कीजिए ।
Sol :
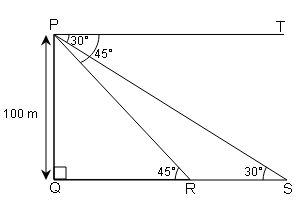
दोनों जहाजों के बीच की दूरी RS
दूसरी जहाज से लाइट हाउस से पाद की दूरी QR
∠PRQ=∠TPR=45°
∠PSQ=∠TPS=30°
ΔPRQ में,
tan θ$=\frac{P}{B}=\frac{PQ}{QR}$
tan 45°$=\frac{100}{QR}$ [Given: PQ=100]
$1=\frac{100}{QR}$
QR=100
ΔPSQ में,
tan θ$=\frac{P}{B}=\frac{PQ}{QS}$
tan 30°=\frac{100}{QS}
$\frac{1}{\sqrt{3}}=\frac{100}{QS}$
QS=100√3
दोनों जहाजों के बीच की दूरी RS
RS=QS-QR
RS=100√3-100
RS=173.2-100
RS=73.2 m
Question 36
(i) जब सूर्य की ऊँचाई 30° से बढ़कर 45° हो जाती है, तो ताड़ के पेड़ की छाया 12 m से कम हो जाती है। ताड़ के पेड़ की ऊँचाई ज्ञात कीजिए।
Sol :
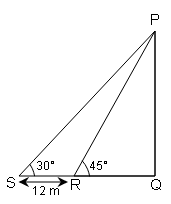
ताड़ के पेड़ की ऊँचाई ( PQ )
बिन्दु R से पेड़ के जड़ की दूरी ( RQ )
ΔPRQ में,
tan θ$=\frac{P}{B}=\frac{PQ}{RQ}$
tan 45°=\frac{PQ}{RQ}
$1=\frac{PQ}{RQ}$
RQ=PQ….(i)
ΔPSQ में,
tan θ$=\frac{P}{B}=\frac{PQ}{SQ}$
tan 30°=\frac{PQ}{SR+RQ}
$\frac{1}{\sqrt{3}}=\frac{PQ}{12+RQ}$
12+RQ=PQ√3
12+PQ=PQ√3 [(i) से]
PQ√3-PQ=12
PQ(√3-1)=12
$PQ=\frac{12}{\sqrt{3}-1}$
$PQ=\frac{12}{\sqrt{3}-1}\times \frac{\sqrt{3}+1}{\sqrt{3}+1}$
$PQ=\frac{12(\sqrt{3}+1)}{{\sqrt{3}}^2-1^2}$
$PQ=\frac{12(\sqrt{3}+1)}{3-1}$
PQ=6(√3+1)
PQ=6(1.732+1)=6×2.732
PQ=16.392 m
ताड़ के पेड़ की ऊँचाई ( PQ )=16.392 m
(ii) एक लम्बा पेड़ नदी के किनारे उधवर्धार खड़ा है । पेड़ के ठीक सामने नदी के दूसरे किनारे पर एक बिन्दु से पेड़ के शिखर का उन्नयन कोण 60° है। उसी किनारे पर इस बिन्दु से 20 m पीछे के एक बिन्दु से पेड़ के शिखर का उन्नयन कोण 30° है। नदी की चौड़ाई और पेड़ की ऊँचाई ज्ञात कीजिए।
Sol :

नदी की चौड़ाई ( QR )
पेड़ की ऊँचाई ( PQ )
ΔPRQ में,
tan θ$=\frac{P}{B}=\frac{PQ}{QR}$
tan 60°=\frac{PQ}{QR}
$\frac{\sqrt{3}}{1}=\frac{PQ}{QR}$
QR√3=PQ…(i)
ΔPQS में,
tan θ$=\frac{P}{B}=\frac{PQ}{QS}$
tan 30°=\frac{PQ}{QS}
$\frac{1}{\sqrt{3}}=\frac{PQ}{QS}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{QR+RS}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{QR+20}$ [Given : RS=20 m]
QR+20=PQ√3
QR+20=(QR√3)√3 [From (i)]
QR+20=3QR
20=3QR-QR
20=2QR
QR=10
∴नदी की चौड़ाई ( QR )=10 m
∴पेड़ की ऊँचाई ( PQ )=QR√3
=10√3 m
Question 37
(i) एक नदी के पुल के एक बिन्दु से नदी के सम्मुख किनारों के अवनमन कोण क्रमश: 30° और 40° हैं। यदि पुल किनारे से 3 m की ऊँचाई पर हो तो नदी की चौड़ाई ज्ञात करें।
Sol :

नदी की चौड़ाई ( QS )
नदी के किनारे के एक बिन्दु से पुल के उस बिन्दु के पाद के पाद की दूरी ( QR )
∠Q=∠APQ=30° (alternate interior angle)
∠S=∠BPS=45°
ΔPQR में,
tan 30°$=\frac{PR}{QR}$
$\frac{1}{\sqrt{3}}=\frac{3}{QR}$ [Given : PR=3 m]
QR=3√3 m
ΔPRS में,
tan 45°$=\frac{PR}{RS}$
$1=\frac{3}{RS}$ [Given : PR=3 m]
RS=3 m
नदी की चौड़ाई=QR+RS
=3√3+3
=3×1.732+3
=8.196 m
(ii) एक 100 m चौड़ी नदी के मध्य में एक छोटा द्वीप है । द्वीप में एक लम्बा पेड़ है। P और Q दो बिन्दुएँ नदी के दोनो किनारो पर ठीक आमने-सामने के बिन्दुएँ है और पेड़ इन बिन्दुओं के सीध में है। यदि P और Q पर पेड़ के उन्नयन कोण क्रमशः 30° और 45° है, तो पेड़ की ऊँचाई ज्ञात कीजिए।
Sol :
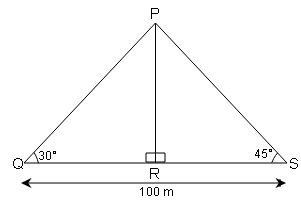
पेड़ की ऊँचाई (PR)
Q बिन्दु से पेड़ के पाद की दूरी ( QR )
ΔPRQ में,
tan 30°$=\frac{PR}{QR}$
$\frac{1}{\sqrt{3}}=\frac{PR}{QR}$
QR=PR√3
ΔPRS में,
tan 45°$=\frac{PR}{RS}$
$1=\frac{PR}{RS}$
RS=PR
QR+RS=100
PR√3+PR=100
PR(√3+1)=100
$PR=\frac{100}{(\sqrt{3}+1)}\times \frac{(\sqrt{3}-1)}{(\sqrt{3}-1)}$
$PR=\frac{100(\sqrt{3}-1)}{(\sqrt{3})^2-1^2}$
$PR=\frac{100(\sqrt{3}-1)}{3-1}$
PR=50(√3-1)
PR=50(1.732-1)
PR=50×0.732=36.6 m
पेड़ की ऊँचाई (PR)=36.6 m
(iii) समुद्र के मध्य में स्थित एक लाइट हाउस की ओर दो जहाज विपरीत दिशाओ से आते हैं । दोनों जहाजों से लाइट-हाउस की ऊँचाई ज्ञात कीजिए।
Sol :

लाइट हाउस की ऊँचाई ( PR )
जहाज से लाइट हाऊस के पाद की दूरी ( QR )
ΔPRQ में,
tan 30°$=\frac{PR}{QR}$
$\frac{1}{\sqrt{3}}=\frac{PR}{QR}$
QR=PR√3
ΔPRS में,
tan 45°$=\frac{PR}{RS}$
$1=\frac{PR}{RS}$
RS=PR
QR+RS=100
PR√3+PR=100
PR(√3+1)=100
$PR=\frac{100}{(\sqrt{3}+1)}\times \frac{(\sqrt{3}-1)}{(\sqrt{3}-1)}$
$PR=\frac{100(\sqrt{3}-1)}{(\sqrt{3})^2-1^2}$
$PR=\frac{100(\sqrt{3}-1)}{3-1}$
PR=50(√3-1)
PR=50(1.732-1)
PR=50×0.732=36.6 m
लाइट हाउस की ऊँचाई ( PR )=36.6 m
(iv) एक लाइट हाउस से इसके विपरीत दिशाओं में स्थित दो जहाजों के कोण क्रमशः 30° और 45° है। यदि लाइट हाउस की ऊँचाई 100 m हो, तो दोनों जहाजों के बीच की दूरी ज्ञात कीजिए यदि दोनों जहाजों को मिलाने वाले रेखा हाउस के पाद से जाती है।
Sol :

दोनों जहाजों के बीच की दूरी ( QS )
जहाज से लाइट हाउस के पाद के दूरी ( QR )
∠A=∠EDA=30° (alternate interior angle)
∠C=∠FDC=45° (alternate interior angle)
ΔPRQ में,
tan 30°$=\frac{PR}{QR}$
$\frac{1}{\sqrt{3}}=\frac{100}{QR}$ [Given : PR=100 m]
QR=100√3 m
ΔPRS में,
tan 45°$=\frac{PR}{RS}$
$1=\frac{100}{RS}$ [Given : PR=100 m]
RS=100
दोनों जहाजों के बीच की दूरी ( QS )
QS=QR+RS
=100√3+100
=173.2+100
=273.2 m
Question 38
एक 30 m लम्बी मूर्ति 15 m ऊँचे स्तम्भ पर खड़ी है । मूर्ति द्वारा स्तम्म के आधार से 15√3 m दूर स्थित बिन्दु पर निर्मित कोण का मान डिग्री में ज्ञात कीजिए ।
Sol :
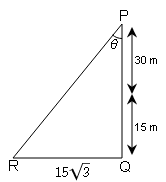
मूर्ति निर्मत कोण θ
tan θ$=\frac{P}{B}=\frac{RQ}{PQ}$
tan θ$=\frac{15\sqrt{3}}{45}$
tan θ$=\frac{1}{\sqrt{3}}$
tan θ=tan 30°
θ=30°
Question 39
एक सीढ़ी एक भवन से लगी है और सीढ़ी के शिखर का उन्नमन कोण 60° है सीढ़ी को पलटकर गली के दूसरे तरफ भवन से लगा दिया जाता है । इस स्थिति में सीढ़ी के शिखर का उन्नयन कोण 45° हों जाता है । यदि सीढ़ी की लम्बाई 26 m हो, तो गली की चौड़ाई ज्ञात कीजिए ।
Sol :
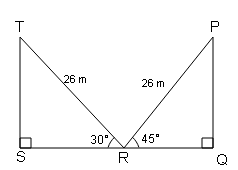
गली की चौड़ाई ( SQ )
एक भवन के पाद से गली में स्थित बिन्दु R की दूरी ( SR )
ΔTRS में,
cos 60°$=\frac{SR}{TR}$
$\frac{1}{2}=\frac{SR}{26}$ [Given : TR=26 m]
$SR=\frac{26}{2}$
SR=13 m
ΔPRQ में,
cos 45°$=\frac{RQ}{PR}$
$\frac{1}{\sqrt{2}}=\frac{RQ}{26}$ [Given : PR=26 m]
$RQ=\frac{26}{\sqrt{2}}$
RQ=13√2 m
गली की चौड़ाई ( SQ )
SQ=SR+RQ
=13+13√2
=13+13×1.414
=31.38
=31.4 m
Question 40
समान ऊँचाई के दो स्तम्भ 64 m की दूरी पर हैं । उनके पादों को मिलाने वाली रेखा के किसी बिन्दु से उनके शिखरों के उन्नयन कोण क्रमशः 30° और 60° हैं । स्तंभों की ऊँचाई ज्ञात करें ।
Sol :
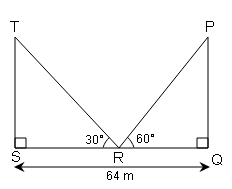
प्रत्येक स्तंभों की ऊँचाई =TS=PQ=x
स्तंभों के पाद से बिन्दु की दूरी क्रमशः SR और RQ
ΔSRT में,
tan 30°$=\frac{TS}{SR}$
$\frac{1}{\sqrt{3}}=\frac{TS}{SR}$
SR=TS√3
या SR=x√3
ΔPRQ में,
tan 60°$=\frac{PQ}{RQ}$
$\sqrt{3}=\frac{PQ}{RQ}$
$RQ=\frac{PQ}{\sqrt{3}}$
या $RQ=\frac{x}{\sqrt{3}}$
SQ=64 m
SR+RQ=64
x√3+$\frac{x}{\sqrt{3}}$=64
$\frac{3x+x}{\sqrt{3}}=64$
4x=64√3
$x=\frac{64\sqrt{3}}{4}$
x=16√3 m
स्तंभों की ऊँचाई (x)=16√3 m
Question 41
दो उध्र्वाधार खम्भों के बीच की दूरी 100 m है और एक की ऊँचाई दूसरें की दुगुनी है । दोनों खम्भों के पादों को मिलाने वाली रेखा पर के किसी बिन्दु पर खम्भों के शिखरों के उन्नयन कोण 60° और 30° हैं। उनकी ऊँचाइयाँ ज्ञात कीजिए ।
Sol :

छोटे स्तंभों की ऊँचाई x
बड़े स्तंभो की ऊँचाई=2x बिन्दु B से दोनों स्तंभों के पाद की दूरी SR तथा RQ
ΔTRS में,
tan 60°$=\frac{TS}{SR}$
$\sqrt{3}=\frac{TS}{SR}$
$\sqrt{3}=\frac{2x}{SR}$
$SR=\frac{2x}{\sqrt{3}}$
ΔPRQ में,
tan 30°$=\frac{PQ}{RQ}$
$\frac{1}{\sqrt{3}}=\frac{x}{RQ}$
RQ=x√3
SQ=100
SR+RQ=100
$\frac{2x}{\sqrt{3}}+x\sqrt{3}=100$
$\frac{2x+3x}{\sqrt{3}}=100$
5x=100√3
x=20√3
छोटे स्तंभों की ऊँचाई x=20√3
बड़े स्तंभो की ऊँचाई=2x =2(20√3)
=40√3
Question 42
30 m चौड़ी सड़क के दोनों तरफ समान ऊँचाई के दो खम्भें है । दोनों खम्भों के बीच स्थिति बिन्दु से उनके शिखरों के उन्नयन कोण क्रमशः 60° और 30° हैं। खम्भों की ऊँचाई एवं बिन्दु की स्थिति ज्ञात कीजिए।
Sol :

स्तंभों की ऊँचाई =TS=PQ=x
बिन्दु B से दोनों स्तंभों के पाद की दूरी SR तथा RQ
ΔPRQ में,
tan 30°$=\frac{PQ}{RQ}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{RQ}$
RQ=PQ√3
या RQ=x√3
ΔTRS में,
tan 60°$=\frac{TS}{SR}$
$\frac{\sqrt{3}}{1}=\frac{TS}{SR}$
$SR=\frac{TS}{\sqrt{3}}$
$SR=\frac{x}{\sqrt{3}}$
SQ=30
SR+RQ=30
$\frac{x}{\sqrt{3}}+x\sqrt{3}=30$
$\frac{x+3x}{\sqrt{3}}=30$
4x=30√3
$x=\frac{30\sqrt{3}}{4}$
x=12.99
स्तंभों की ऊँचाई =TS=PQ=x=12.99 m
बिन्दु B से दोनों स्तंभों के पाद की दूरी SR तथा RQ
$SR=\frac{x}{\sqrt{3}}=\dfrac{\frac{30\sqrt{3}}{4}}{\sqrt{3}}$
$SR=\frac{30}{4}$
SR=7.5 m
RQ=x√3
RQ$=\frac{30\sqrt{3}}{4} \times \sqrt{3}$
$RQ=\frac{90}{4}$
RQ=22.4 m
Question 43
एक पेड़ के आधार से एक मीनार के शिखर का उन्नयन कोण 60° है और मीनार के आधार से पेड़ के शिखर का उन्नयन कोण 30° है । यदि मीनार की उँचाई 50 m हो, तो पेड़ की ऊचाई ज्ञात कीजिए।
Sol :
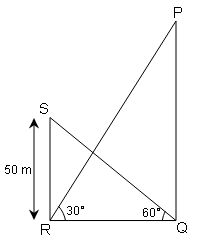
पेड़ की ऊँचाई ( PQ )
पेड़ तथा मीनार के पाद की दूरी ( RQ )
tan 30°=\frac{PQ}{RQ}
$\frac{1}{\sqrt{3}}=\frac{PQ}{RQ}$
$PQ=\frac{RQ}{\sqrt{3}}$
tan 60°$=\frac{SR}{RQ}$ [Given : SR=50 m]
$\sqrt{3}=\frac{50}{RQ}$
$RQ=\frac{50}{\sqrt{3}}$
पेड़ की ऊँचाई ( PQ )
$PQ=\frac{RQ}{\sqrt{3}}$
$PQ=\dfrac{\frac{50}{\sqrt{3}}}{\sqrt{3}}$
$PQ=\frac{50}{\sqrt{3}}\times \frac{1}{\sqrt{3}}$
$PQ=\frac{50}{3}=16\frac{2}{3}$
Question 44
कोई उधर्वाधर मीनार 10 m ऊँचे झंडे के खम्भे की चोटी पर समकोण बनाती हैं। यदि उनके बीच की दूरी 10 m हो तो मीनार की ऊँचाई ज्ञात करें।
Sol :

PQ=PQ=10 m
∠PRQ=∠QPR=45°
∠SPR=∠QRP=45° (alternate interior angle)
∠RPT=90° (given)
∠SPR+∠TPS=90°
45°+∠TPS=90°
∠TPS=90°-45°=45°
∠TPS=45°
ΔTPS मे,
tan 45°$=\frac{TS}{SP}$
$1=\frac{TS}{10}$ [Given : SP=10 m]
TS=10 m
मीनार की ऊँचाई=AE+DE
=10+10=20 m
Question 45
एक चट्टान के शिखर का उन्नयन कोण 100 m ऊँचे मीनार के शिखर और पाद से क्रमशः 30° और 45° हैं। चट्टान की ऊँचाई ज्ञात कीजिए । .
Sol :
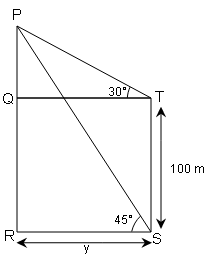
चट्टान की ऊँचाई PR=PQ+QR या
=PQ+TS=PQ+100
चट्टान के पाद से मीनार के पाद की दूरी ( RS )=QT=y
ΔPSR में,
tan 45°$=\frac{PR}{RS}$
$1=\frac{PR}{RS}$
RS=PR
RS=PQ+QR
RS=PQ+TS
RS=PQ+100…(i)
ΔPTQ में,
tan 30°$=\frac{PQ}{QT}$
$\frac{1}{\sqrt{3}}=\frac{PQ}{RS}$
RS=PQ√3….(ii)
(i) और (ii) से,
PQ+100=PQ√3
PQ√3-PQ=100
PQ(√3-1)=100
PQ(1.732-1)=100
$PQ=\frac{100}{0.732}$
PQ=136.61
चट्टान की ऊँचाई PR=PQ+QR
PR=136.61+100
PR=236.61
Question 46
एक मीनार के शिखर से 7 m ऊँचे भवन के शिखर और पाद के अवनमन कोण क्रमशः 45° और 60° हैं। मीनार की ऊँचाई ज्ञात कीजिए ।
Sol :
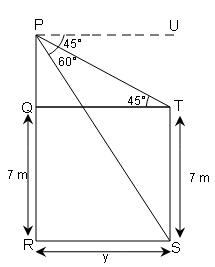
मीनार की ऊँचाई ( PR )
मीनार के पाद तथा भवन के पाद के बीच की दूरी RS=QT
∠UPT=∠PTQ=45° (alternate interior angle)
∠PSR=∠TPS=60° (alternate interior angle)
ΔPTQ में,
tan 45°$=\frac{PQ}{QT}$
$1=\frac{PQ}{RS}$
RS=PQ….(i)
ΔPSR में,
tan 60°$=\frac{PR}{RS}$
$\frac{\sqrt{3}}{1}=\frac{PR}{RS}$
RS√3=PR
PQ√3=PQ+QR
PQ√3-PQ=7
PQ(√3-1)=7
PQ(1.732-1)=7
$PQ=\frac{7}{0.732}$
PQ=9.56 m
मीनार की ऊँचाई ( PR )
PR=PQ+QR
=9.56+7
=16.56 m
Question 47
एक भवन सड़क के दूसरी तरफ के खम्भे के शिखर पर समकोण बनाता है । खम्भ एवं भवन के शिखरों को मिलाने वाली रेखा उदग्र (vertical) के साथ 60° का कोण बनाती है । यदि सड़क की चौड़ाई 45m है, तो भवन की ऊँचाई ज्ञात कीजिए ।
Sol :
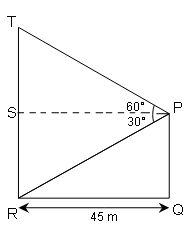
भवन की ऊँचाई ( TR )
TR=TS+SR
सड़क की चौड़ाई 45m =SP=RQ
∠TPS+∠SPR=90°
60°+∠SPR=90°
∠SPR=90°-60°=30°
ΔSPR में,
tan 30°$=\frac{}{SP}$
$\frac{1}{\sqrt{3}}=\frac{SR}{45}$
$\frac{45}{\sqrt{3}}=SR$
$SR=\frac{45}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
SR=15√3 m
ΔTPS में,
tan 60°$=\frac{TS}{SP}$
$\sqrt{3}=\frac{TS}{45}$
TS=45√3 m
भवन की ऊँचाई ( TR )
TR=TS+SR
=15√3 m+45√3 m
=60√3 m
Question 48
h मीटर ऊँचे भवन की चोटी और पाद से एक मीनार की चोटी का उन्नयन कोण क्रमशः $\alpha$ और $\beta$ हैं। सिद्ध करें कि मीनार की ऊँचाई $\frac{h \tan \beta}{\tan \beta-\tan \alpha}$ है ।
Sol :

मीनार की ऊँचाई ( PR )
PR=PQ+QR
मीनार के पाद से भवन के पा की बीच की दूरी QT=RS=y
tan ⍺$=\frac{PQ}{QT}$
tan ⍺$=\frac{PQ}{RS}$
RS$=\frac{PQ}{\tan \alpha}$
ΔPSR,
tan β$=\frac{PR}{RS}$
tan β$=\frac{PQ+QR}{RS}$
$\tan \beta \times \frac{PQ}{\tan \alpha}=PQ+h$
$\frac{ \tan \beta}{\tan \alpha}=\frac{PQ+h}{PQ}$
$\frac{ \tan \beta}{\tan \alpha}=\frac{PQ+h}{PQ}$
$\frac{ \tan \beta}{\tan \alpha}=1+\frac{h}{PQ}$
$\frac{ \tan \beta}{\tan \alpha}-1=\frac{h}{PQ}$
$\frac{ \tan \beta-\tan \alpha}{\tan \alpha}=\frac{h}{PQ}$
$\frac{\tan \alpha}{ \tan \beta-\tan \alpha}=\frac{PQ}{h}$
$PQ=\frac{h\tan \alpha}{ \tan \beta-\tan \alpha}$
मीनार की ऊँचाई ( PR )
PR=PQ+QR
PR=PQ+h
PR$=\frac{h\tan \alpha}{\tan \beta-\tan \alpha}+h$
PR=\frac{h\tan \alpha+h(\tan \beta-\tan \alpha)}{\tan \beta-\tan \alpha}
PR=\frac{h\tan \alpha+h\tan \beta-h\tan \alpha}{\tan \beta-\tan \alpha}
PR=\frac{h\tan \beta}{\tan \beta-\tan \alpha}
Question 49
जमीन पर के किसी बिन्दु P से एक वायुयान का उन्नयन कोण 60° है। 30 सेकेण्ड की उड़ान के बाद उन्नयन कोण 30° हो जाता है । यदि वायुयान $3600 \sqrt{3} \mathrm{~m}$ की अचर ऊँचाई पर उड़ रहा है तो वायुयान की गति कि.मी./घंटा में ज्ञात कीजिए ।
Sol :
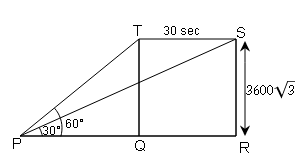
बिन्दु P से वायुयान x मी दूरी तय किया
30 sec बाद तय की गई y
TQ=SR=3600√3
ΔTPQ में,
tan 60°$=\frac{TQ}{PQ}$
$\sqrt{3}=\frac{3600\sqrt{3}}{PQ}$
PQ=\frac{3600\sqrt{3}}{\sqrt{3}}
PQ=3600
ΔSPR में,
tan 30°$=\frac{SR}{PR}$
$\frac{1}{\sqrt{3}}=\frac{3600\sqrt{3}}{PR}$
PR=3600√3×√3
PR=3600×3=10800 m
PR=PQ+QR
10800=3600+QR
QR=10800-3600=7200 m
QR=7.2 km
30 sec ⟶$\frac{1}{120}$ hr
वायुयान का चल$=\dfrac{7.2}{\frac{1}{120}}$ km/hr
$=\frac{7.2}{1}\times \frac{120}{1}$
=864 km/hr
Question 50
जमीन पर के किसी बिन्दु P से एक जेट-फाइटर का उन्नमन कोण 60° है । 10 सेकेण्ड की उड़ान के बाद उन्नयन कोण 30° हो जाता है । यदि जेट 432 कि.मी./घंटा की चाल से उड़ रहा है तो वह अचर ऊँचाई ज्ञात कीजिए जिस पर जेट उड़ रहा है ।
Sol :
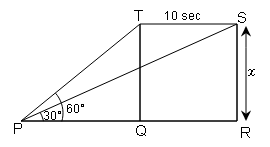
जेट फाइटर की ऊँचाई x
चाल = 432 km/hr
समय=10 sec ⟶$\frac{1}{360}$ hr
चाल =दूरी/समय
$432=\frac{TS}{\frac{1}{360}}$
$TS=\frac{432}{360}$
TS=1.2 km
or 1200 m
TS=QR=1200 m
बिन्दु P से जेट-फाइटर के लंब पाद की प्रारंभिक दूरी ( PQ )
TQ=SR
ΔTPQ में,
tan 60°$=\frac{TQ}{PQ}$
$\sqrt{3}=\frac{SR}{PQ}$
PQ√3=SR
ΔSPR में,
tan 30°$=\frac{SR}{PR}$
$\frac{1}{\sqrt{3}}=\frac{SR}{PQ+QR}$
$\frac{1}{\sqrt{3}}=\frac{SR}{PQ+1200}$ [Given : TS=QR]
$\frac{PQ+1200}{\sqrt{3}}=PQ\sqrt{3}$
PQ+1200=PQ√3×√3
PQ+1200=3PQ
1200=3PQ-PQ
1200=2PQ
$PQ=\frac{1200}{2}$
PQ=600 m
SR=PQ√3
SR=600√3 m
