KC Sinha: Exercise 5.3 – Mathematics Solution Class 10 Chapter 5 Triangles

Question 1 

State which of the following pairs of triangles are similar. Write the similarity criterion used and write the pairs of similar triangles in symbolic form (all lengths of sides are in cm).

(i) 

(ii) 
(iii) 

(iv) 

(v) 

(vi) 


(vii) 

Sol :
(i) In ΔABC,
∠A = 70° and ∠B = 50°
And we know that, sum of the angles = 180°
⇒∠A + ∠B +∠C = 180°
⇒70° + 50° +∠C = 180°
⇒ 120° +∠C = 180°
⇒ ∠C = 60°

And In ΔDEF
∠F = 70° and ∠E = 50°
And we know that, sum of the angles = 180°
⇒∠D + ∠E +∠F = 180°
⇒∠D + 50° + 70° = 180°
⇒ ∠D = 60°
Yes,ΔABC ~ ΔDEF [by AAA similarity criterion]

(ii) In ΔABC and ΔPQR
Here,[Math Processing Error], [Math Processing Error], [Math Processing Error]

As,[Math Processing Error]
So, ΔABC ~ ΔPQR [by SSS similarity criterion]

(iii) InΔMNL and ΔPQR
∠NML = ∠PQR = 70°

[Math Processing Error]
[Math Processing Error]
and [Math Processing Error]
[Math Processing Error]

No, the two triangles are not similar.

(iv) In ΔPQR and ΔLMN
∠PQR = ∠LNM = 50°
[Math Processing Error]
and [Math Processing Error]
[Math Processing Error]
∴ΔPQR ~ ΔLMN [by SAS similarity criterion]

(v) In ΔLMP and ΔDEF
Here,[Math Processing Error] 

[Math Processing Error], [Math Processing Error], [Math Processing Error]

As[Math Processing Error]
So, no two triangles are not similar

(vi) In ΔABC and ΔPQR
∠A = ∠Q = 85°
∠B = ∠P = 60°
and ∠C =∠R = 35°
So, ΔPQR ~ ΔLMN [by AAA similarity]

(vii) In ΔABC and ΔPQR
Here,[Math Processing Error],[Math Processing Error], [Math Processing Error]
As,[Math Processing Error]
So, ΔABC ~ ΔPQR [by SSS similarity criterion]

Question 2 

If diagonals AC and BD of trapezium ABCD with AB || CD intersect each other at 0 and AB= 18 cm, DC = 30 cm, OB =y cm, OD= 10 cm, find y.

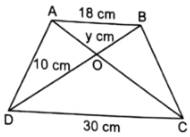
Sol :
Given: ABCD is a trapezium with AB || CD
and diagonals AB and CD intersecting at O
To find: y
Firstly, we prove that ΔOAB ~ ΔODC
Let ΔOAB and ΔODC
∠AOB = ∠COD [vertically opposite angles]
∠OBA = ∠ODC [∵AB || CD with BD as transversal.
alternate angles are equal]
∠OAB = ∠OCD [∵AB || CD with BD as transversal.
alternate angles are equal]

∴ ΔOAB ~ ΔODC [by AAA similarity]
Since triangles are similar. Hence corresponding sides are proportional.
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
⇒ y = 6cm

Question 3 

In the given figure BC = 5 cm, AC = 5.5 cm and AB= 4.6 cm. P and Q are points on AB and AC respectively such that PQ || BC. If PQ = 2.5 cm, find other sides of ΔAPQ.

Sol :
Given: PQ || BC
To find: AP and AQ
Since, PQ || BC, AB is transversal, then,
ΔAPQ = ΔABC [by corresponding angles]
Since, PQ || BC, AC is transversal, then,
ΔAPQ = ΔABC [by corresponding angles]
In ΔAPQ andΔABC
∠APQ = ∠ABC
∠AQP = ∠ACB

∴ ΔAPQ ≅ ΔABC [by AAA similarity]
Since, the corresponding sides of similar triangles are proportional
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
⇒AP = 2.3

Now, taking [Math Processing Error]
[Math Processing Error]
[Math Processing Error]
⇒AQ = 2.75
Therefore, AP = 2.3cm and AQ = 2.75cm

Question 4 

In the given figure ΔABR ~ ΔPQR, if PQ = 30 cm, AR = 45 cm, AP = 72 cm and QR = 42 cm, find PR and BR.

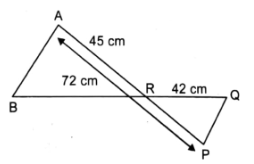
Sol :
Given: ΔABR ~ ΔPQR
As, ΔABR and ΔPQR are similar
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
⇒BR = 70cm
and PR = AP – AR = 72 – 45 = 27cm

Question 5

In the given figure, QA and PB are perpendiculars to AB. If AO = 10 cm, BO = 6 cm and PB = 9 cm, find AQ.

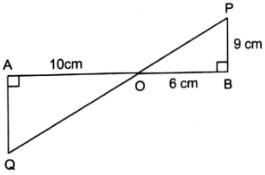
Sol :
Let us take ΔOAQ and ΔOBP
∠AOQ = ∠BOP (vertically opposite angles)
∠OAQ = ∠OBP (each 90°)
∴ ΔOAQ ~ΔOBP (by AA similarity criterion)
Given: AO = 10 cm, BO = 6 cm and PB = 9 cm
As, ΔOAQ ~ΔOBP
[Math Processing Error]
[Math Processing Error]
⇒AQ = 15cm

Question 6 

In the given figure ΔACB ~ ΔAPQ, if BC = 8 cm, PQ = 4 cm, BA = 6.5 cm, AP= 2.8 cm, Find CA and AQ.

Sol :
Given: ΔACB ~ ΔAPQ
As, ΔACB and ΔAPQ are similar
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
Taking [Math Processing Error]

⇒CA = 5.6cm
Now, taking [Math Processing Error]
⇒AQ =3.25cm

Question 7 

In the given figure, XY || BC. Find the length of XY, given BC = 6 cm.

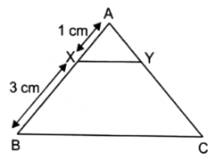
Sol :
Given: XY || BC
To find: XY
Since, XY || BC, AB is transversal, then,
ΔAXY = ΔABC [by corresponding angles]
Since, XY || BC, AC is transversal, then,
ΔAYX = ΔABC [by corresponding angles]
In ΔAXY andΔABC
∠AXY = ∠ABC
∠AYX = ∠ACB
∴ ΔAXY ≅ ΔABC [by AA similarity]
Since, triangles are similar, hence corresponding sides will be proportional
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
⇒XY = 1.5
Therefore, XY= 1.5cm

Question 8 

The perimeters of two similar triangles, ABC and PQR (ΔABC~ ΔPQR) are respectively 72 cm and 48 cm. If PQ = 20 cm, find AB.

Sol :
Given: ΔABC~ΔPQR, PQ =20cm
And perimeter of ΔABC andΔPQR are 72cm and 48cm respectively.
As, ΔABC ~ΔPQR
[Math Processing Error] (corresponding sides are proportional)
[Math Processing Error][Math Processing Error]
[Math Processing Error]

[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
⇒AB = 30cm

Question 9 

In the given figure, if PQ || RS, prove that ΔPOQ ~ Δ SOR.

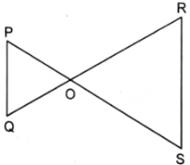
Sol :
Given: PQ || RS
To Prove: ΔPOQ ~ΔSOR
Let us takeΔPOQ andΔSOR
∠OPQ = ∠OSR (as PQ || RS, Alternate angles)
∠POQ = ∠ROS (vertically opposite angles)
∠OQP = ∠ORS (as PQ || RS, Alternate angles)
∴ ΔPOQ ~ΔSOR (by AAA similarity criterion)
Hence Proved

Question 10 

In the given figure, if ∠A = ∠C, then prove that Δ AOB ~ Δ COD

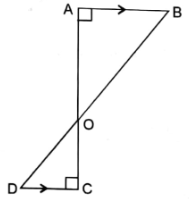
Sol :
Given: ∠A = ∠C
To Prove: ΔAOB ~ΔCOD
Let us take ΔAOB andΔCOD
∠A = ∠C (given)
∠AOB = ∠COD (vertically opposite angles)
∴ ΔAOB ~ΔCOD (by AA similarity criterion)
Hence Proved

Question 11 

In the given figure DB ⊥ BC, DE ⊥ AB and AC ⊥ BC, prove that ΔBDE ~ΔABC.

Sol :
We have, DB 丄 BC and AC 丄 BC
∠B + ∠C = 90° + 90°
⇒ ∠B + ∠C = 180°
∴ BD || AC
⇒∠EBD = ∠CAB (alternate angles)
Let us take ΔBDE andΔABC
∠BED = ∠ACB (each 90°)
∠EBD = ∠CAB (alternate angles)
∴ ΔBDE ~ΔABC (by AA similarity criterion)
Hence Proved

Question 12 

In the given figure, ∠1 =∠2 and [Math Processing Error], prove that ΔACB ~ ΔDCE

Sol :

We have, [Math Processing Error]
[Math Processing Error]
[Math Processing Error] (∵, BD = DC as ∠1 = ∠2) …(i)
Also, ∠1 = ∠2
i.e. ∠DBC = ∠ACB
∴ ΔACB ~ ΔDCE (by SAS similarity criterion)
Hence Proved

Question 13 

In an isosceles ΔABC with AC = BC, the base AB is produced both ways to P and Q such that AP x BQ = AC². Prove that : ΔACP ~ ΔBQC

Sol :
Given ABC is an isosceles triangle and AC = BC
∵ AC = BC
⇒∠CAB = ∠CBA
⇒180° – ∠CAB = 180° – ∠CBA
⇒ ∠CAP = ∠CBQ
Also, AP x BQ = AC²
[Math Processing Error]
[Math Processing Error] (∵ AC =BC)

Thus, by SAS similarity, we get
ΔACP ~ ΔBQC
Hence Proved

Question 14 

In the given figure, find ∠P.

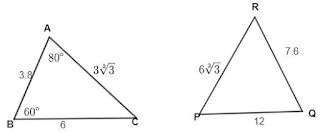
Sol :
From the figure,
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]

Hence, [Math Processing Error]

Now it can be seen that both the triangles are similar as the corresponding sides are propotional.
From the figure we can see that,
∠ P = ∠ C
From ΔABC,
∠ A + ∠ B + ∠ C = 180°
60° + 80° + ∠ C = 180°
∠ C = 180° – 140°
∠ C = 40°
Hence, ∠ P = 40°

Question 15 

P and Q are points on the sides AB and AC respectively of a ΔABC. If AP = 2 cm, PB = 4 cm, AQ = 3 cm and QC = 6 cm, show that BC = 3 PQ.

Sol :

Here, [Math Processing Error]
and [Math Processing Error]
[Math Processing Error]

∴ PQ || BC [by converse of basic proportionality theorem]
Now, take ΔAPQ and ΔABC
∠APQ = ∠ABC (corresponding angles)
∠AQP = ∠ACB (corresponding angles)

∴ ΔAPQ ~ ΔABC (by AA similarity criterion)

Since, triangles are similar, hence corresponding sides will be proportional
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
⇒BC = 3PQ
Hence Proved

Question 16 

P and Q are respectively the points on the sides AB and AC of a ΔABC. If AP = 2 cm, PB = 6 cm, AQ = 3 cm and QC = 9, Prove that BC = 4PQ.

Sol :

Here, [Math Processing Error]
and [Math Processing Error]
[Math Processing Error]

∴ PQ || BC [by the converse of basic proportionality theorem]
Now, take ΔAPQ and ΔABC
∠APQ = ∠ABC (corresponding angles)
∠AQP = ∠ACB (corresponding angles)
∴ ΔAPQ ~ ΔABC (by AA similarity criterion)

Since, triangles are similar, hence corresponding sides will be proportional
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
⇒BC = 4PQ
Hence Proved

Question 17 

In the given figure, [Math Processing Error] and AB = 5 cm. Find the value of DC.

Sol :
In ΔAOB and ΔCOD,
∠ AOB = ∠COD (Vertically opposite angles)
 [Math Processing Error](given)
Therefore according to SAS similarity criterion,
∴ ΔAOB ~ ΔCOD

Since, triangles are similar, hence corresponding sides will be proportional
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
⇒ DC = 10cm

Question 18 

In the given figure, OA .OB = OC.OD, show that: ∠A = ∠C and ∠B = ∠D.

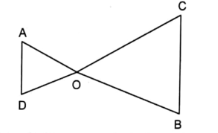
Sol :
Given: OA × OB = OC × OD
To Prove: ∠A = ∠C and ∠B = ∠D
Now, OA .OB = OC.OD
 [Math Processing Error]…(i)

In △AOD and △COB
[Math Processing Error] (from (i))
∠AOD = ∠COB (vertically opposite angles)
∴ △AOD ~ △COB (by SAS similarity criterion)
We know that if two triangles are similar then their corresponding angles are equal.
⇒ ∠A = ∠C and ∠B = ∠D
Hence Proved

Question 19 

In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ~ ΔPQR, prove that:

(i) ΔAMC ~ ΔPNR
(ii) [Math Processing Error]
(iii) ΔCMB ~ ΔRNQ

Sol :
Given: CM is the median of △ABC and RN is the median of △PQR
Also, △ABC ~ △PQR
To Prove: (i) △AMC ~△PNR
CM is median of △ABC

So, [Math Processing Error] …(1)

Similarly, RN is the median of △PQR
So, [Math Processing Error] …(2)

Given △ABC ~△PQR
[Math Processing Error]
(corresponding sides of similar triangle are proportional)
[Math Processing Error]
[Math Processing Error] (from (1) and (2))

[Math Processing Error] …(3)

Also, since △ABC ~△PQR
∠A = ∠P …(4)
(corresponding angles of similar triangles are equal)

In △AMC and △PNR

∠A = ∠P (from (4))
[Math Processing Error] (from (3))
∴ △AMC ~△PNR (by SAS similarity)
Hence Proved

(ii)To Prove:[Math Processing Error]
In part (i), we proved that △AMC ~△PNR
So, [Math Processing Error]
(corresponding sides of a similar triangle are proportional)
Therefore, [Math Processing Error]
[Math Processing Error]
[Math Processing Error]
Hence Proved

(iii) △CMB ~△RNQ
Given △ABC ~△PQR
[Math Processing Error]
(corresponding sides of similar triangle are proportional)
[Math Processing Error]
[Math Processing Error] (from (1) and (2))
[Math Processing Error] …(5)
Also, since △ABC ~△PQR
∠B = ∠Q …(6)
(corresponding angles of similar triangles are equal)
In △CMB and △RNQ
∠B = ∠Q (from (6))
[Math Processing Error] (from (5))
∴ △CMB ~△RNQ (by SAS similarity)
Hence Proved

Question 20 

In the adjoining figure, the diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC. Show that DF x FE = BF x FA.

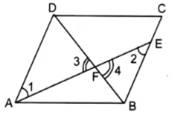
Sol :
Given: ABCD is a parallelogram
To Prove: DF x FE = BF x FA
In △AFD and △BFE
∠1 = ∠2 (alternate angles)
∠3 = ∠4 (vertically opposite angles)
∴ △AFD ~△BFE (by AA similarity criterion)
So, [Math Processing Error]
(corresponding sides of similar triangle are proportional)
[Math Processing Error]
⇒ DF x FE = BF x FA
Hence Proved

Question 21 

In the given figure, DEFG is a square and ∠BAC is a right angle. Show that DE²= BD x EC.

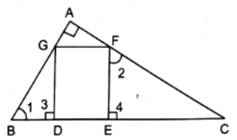
Sol :
Given: DEFG is a square and ∠BAC = 90°
To Prove: DE² = BD × EC.
In △AGF and △DBG
∠GAF = ∠BDG [each 90°]
∠AGF = ∠DBG
[corresponding angles because GF|| BC and AB is the transversal]
∴△AFG ~ △DBG [by AA Similarity Criterion] …(1)
In △AGF and △EFC
∠GAF = ∠CEF [each 90°]
∠AFG = ∠ECF
[corresponding angles because GF|| BC and AC is the transversal]
∴△AGF ~△EFC [by AA Similarity Criterion] …(2)
From equation (1) and (2), we have
△DBG ~ △EFC
Since, the triangle is similar. Hence corresponding sides are proportional
[Math Processing Error]
[Math Processing Error] [∵DEFG is a square]
⇒DE² = BD × EC
Hence Proved

Question 22 

In the given figure, ABD is a right angled triangle being right angled at A and AD ⊥ BC. Show that:

(i) AB²= BC.BD
(ii) AC² = BC. DC
(iii) AB. AC. = BC. AD
Sol :
(i) In ΔDAB and ΔACB
∠ADB = ∠CAB [each 90°]
∠DAB = ∠CAB [common angle]
∴ △DAB ~△ACB [by AA similarity]

Since the triangles are similar, hence corresponding sides are in proportional.
[Math Processing Error]
⇒ AB²= BC×BD

(ii) In △ACB and △DAC

∠CAB = ∠ADC [each 90°]
∠CAB = ∠CAD [common angle]
∴ △ACB ~△DAC [by AA similarity]
Since the triangles are similar, hence corresponding sides are in proportional.
[Math Processing Error]
⇒ AC² = BC. DC

(iii) In part (i) we proved that △DAB ~△ACB
[Math Processing Error]
⇒ AB × AC = BC × AD
Hence Proved

Question 23 

In the given figure, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.

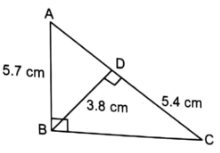
Sol :
Given: ∠ABC = 90° and BD丄 AC
and AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm
To find: BC
Firstly, we have to show that △ABC ~△BDC
Let △ABC and △BDC
∠ABC = ∠BDC [each 90°]
∠ACB = ∠BCD [common angle]
∴ △ABC ~△BDC [by AA similarity criterion]
Since, triangles are similar, hence corresponding sides are proportional.
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
⇒ BC = 8.1cm

Question 24 

In the given figure, ∠CAB =90° and AD ⊥ BC. Show that ΔBDA ~ ΔBAC. If AC = 75 cm, AB = 1 cm and BC = 1.25 cm, find AD.

Sol :
Given: ∠CAB =90° and AD丄 BC
and AC = 75 cm, AB = 1 cm and BC = 1.25 cm
Now, In △ADB and △CAB

∠ADB = ∠CAB [each 90°]
∠ABD = ∠CBA [common angle]
∴ △ADB ~△CAB [by AA similarity]
Since the triangles are similar, hence corresponding sides are in proportional.
[Math Processing Error]
[Math Processing Error]
⇒ AD = 60cm