Contents
- 1 Question 1
- 2 Question 2
- 3 Question 3 A
- 4 Question 3 B
- 5 Question 3 C
- 6 Question 3 D
- 7 Question 3 E
- 8 Question 3 F
- 9 Question 3 G
- 10 Question 3 H
- 11 Question 3 I
- 12 Question 3 J
- 13 Question 3 K
- 14 Question 3 L
- 15 Question 3 M
- 16 Question 3 N
- 17 Question 4 A
- 18 Question 4 B
- 19 Question 4 C
- 20 Question 4 D
- 21 Question 4 E
- 22 Question 4 F
- 23 Question 4 G
- 24 Question 4 H
- 25 Question 4 I
- 26 Question 5 A
- 27 Question 5 B
- 28 Question 5 C
- 29 Question 5 D
- 30 Question 5 E
- 31 Question 5 F
- 32 Question 5 G
- 33 Question 5 H
- 34 Question 5 I
- 35 Question 5 J
- 36 Question 5 K
- 37 Question 5 L
- 38 Question 5 M
- 39 Question 5 N
- 40 Question 6A
- 41 Question 6 B
- 42 Question 6 C
- 43 Question 7 A
- 44 Question 7 B
- 45 Question 8 A
- 46 Question 8 B
- 47 Question 9
- 48 Question 10
- 49 Question 11
- 50 Question 12
- 51 Question 13 A
- 52 Question 13 B
- 53 Question 13 C
- 54 Question 13 D
- 55 Question 14
- 56 Question 15
Question 1
Find the value of the following :
(i) sin 30o + cos 60o
(ii) sin2 45o+cos245o
(iii) sin 30o + cos 60o – tan45o
(iv) $\sqrt{1+\tan ^{2} 60^{\circ}}$
(v) tan 60o x cos30o
Sol :
(i) sin 30o + cos 60o
We know that,
$\sin \left(30^{\circ}\right)=\frac{1}{2}>\cos \left(60^{\circ}\right)=\frac{1}{2}$
So,
sin(30o) + cos(60o)
$=\left(\frac{1}{2}\right)+\left(\frac{1}{2}\right)$
=1
(ii) sin2 45o+cos245o
We know that,
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
So, sin2 45o+cos245o
$=\left(\frac{1}{\sqrt{2}}\right)^{2}+\left(\frac{1}{\sqrt{2}}\right)^{2}$
$=\left(\frac{1}{2}\right)+\left(\frac{1}{2}\right)$
=1
(iii) sin 30o + cos 60o – tan45o
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
tan(45o)=1
So,
sin 30o + cos 60o – tan 45o
$=\left(\frac{1}{2}\right)+\left(\frac{1}{2}\right)-1$
$=\frac{1+1-2}{2}$
=0
(iv) $\sqrt{1+\tan ^{2} 60^{\circ}}$
We know that
tan(60o) = √3
So,
$=\sqrt{1+\tan ^{2} 60^{\circ}}$
$=\sqrt{1+(\sqrt{3})^{2}}$
$=\sqrt{1+3}$
=√4
= 2
(v) tan 60o × cos30o
tan(60o) = √3
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
So,
tan 60o × cos30o
$=\sqrt{3} \times \frac{\sqrt{3}}{2}$
$=\frac{3}{2}$
Question 2
If θ = 45°, find the value of
(i) $\tan ^{2} \theta+\frac{1}{\sin ^{2} \theta}$
(ii) cos2 θ – sin2 θ
Sol :
(i) $\tan ^{2} \theta+\frac{1}{\sin ^{2} \theta}$
Given θ =45°
We know that,
tan(45o) = 1
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$=(1)^{2}+\frac{1}{\left(\frac{1}{\sqrt{2}}\right)^{2}}$
= 1+ 2
= 3
(ii) cos2 θ – sin2 θ
Given θ = 45°
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
So, cos2 45° – sin2 45°
$=\left(\frac{1}{\sqrt{2}}\right)^{2}-\left(\frac{1}{\sqrt{2}}\right)^{2}$
= 0
Question 3 A
Find the numerical value of the following :
sin45°.cos45° – sin230°.
Sol :
We know that,
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
Now, putting the values
$=\left(\frac{1}{\sqrt{2}}\right) \times\left(\frac{1}{\sqrt{2}}\right)-\left(\frac{1}{2}\right)^{2}$
$=\left(\frac{1}{2}\right)-\left(\frac{1}{4}\right)$
$=\left(\frac{1}{4}\right)$
Question 3 B
Find the numerical value of the following :
$\frac{\tan 60^{\circ}}{\sin 60^{\circ}+\cos 60^{\circ}}$
Sol :
We know that,
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
tan (60°) = √3
Now putting the values;
$=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}+\frac{1}{2}}$
$=\frac{\frac{\sqrt{3}}{1+\sqrt{3}}}{2}$
$=\sqrt{3} \times \frac{2}{1+\sqrt{3}}$
$=\frac{2 \sqrt{3}}{1+\sqrt{3}}$
Multiplying and dividing by the conjugate of (1+√3)
$=\frac{2 \sqrt{3}}{1+\sqrt{3}} \times \frac{1-\sqrt{3}}{1-\sqrt{3}}$
$=\frac{2 \sqrt{3}-6}{(1)^{2}-(\sqrt{3})^{2}}$ [∵(a)2 – (b)2 = (a+b)(a-b)]
$=\frac{2 \sqrt{3}-6}{-2}$
Multiplying and dividing by (-2)
= 3 – √3
Question 3 C
Find the numerical value of the following :
$\frac{\tan 60^{\circ}}{\sin 60^{\circ}+\cos 30^{\circ}}$
Sol :
We know that,
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
tan (60o) = √3
Now putting the values;
$=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}}$
$=\frac{\sqrt{3}}{\sqrt{3}}$
= 1
Question 3 D
Find the numerical value of the following :
$\frac{4}{\sin ^{2} 60^{\circ}}+\frac{3}{\cos ^{2} 60^{\circ}}$
Sol :
We know that
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
Now putting the value, we get
$=\frac{4}{\left(\frac{\sqrt{3}}{2}\right)^{2}}+\frac{3}{\left(\frac{1}{2}\right)^{2}}$
$=4 \times\left(\frac{2}{\sqrt{3}}\right)^{2}+3 \times(2)^{2}$
$=4\left(\frac{4}{3}\right)+3 \times 4$
$=\frac{16}{3}+12$
$=\frac{16+36}{3}$
$=\frac{52}{3}$
Question 3 E
Find the numerical value of the following :
sin2 60° – cos2 60°
Sol :
We know that,
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
Now putting the value;
$=\left(\frac{\sqrt{3}}{2}\right)^{2}-\left(\frac{1}{2}\right)^{2}$
$=\left(\frac{3}{4}\right)-\left(\frac{1}{4}\right)$
$=\frac{1}{2}$
Question 3 F
Find the numerical value of the following :
4sin2 30° + 3 tan 30° – 8 sin 45° cos 45°
Sol :
We know that,
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
$\tan \left(30^{\circ}\right)=\frac{1}{\sqrt{3}}$
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
Now putting the value, we get
$=4 \times\left(\frac{1}{2}\right)^{2}+3 \times\left(\frac{1}{\sqrt{3}}\right)^{2}-8 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}$
$=4 \times \frac{1}{4}+3 \times \frac{1}{3}-8 \times \frac{1}{2}$
= 1 + 1 – 4
= -2
Question 3 G
Find the numerical value of the following :
2sin230° – 3cos2 45° + tan2 60ׄ°
Sol :
We know that,
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
Tan (60o) = √3
Now putting the value;
$=2 \times\left(\frac{1}{2}\right)^{2}-3 \times\left(\frac{1}{\sqrt{2}}\right)^{2}+(\sqrt{3})^{2}$
$=2 \times \frac{1}{4}-3 \times \frac{1}{2}+3$
$=\frac{1}{2}-\frac{3}{2}+3$
$=\frac{1-3+6}{2}$
$=\frac{4}{2}$
=2
Question 3 H
Find the numerical value of the following :
sin 90° + cos 0° + sin 30° + cos 60°
Sol :
We know that,
Sin (90o) = 1
Cos (0o) = 1
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
Now putting the value;
$=1+1+\frac{1}{2}+\frac{1}{2}$
$=\frac{2+2+1+1}{2}$
$=\frac{6}{2}$
= 3
Question 3 I
Find the numerical value of the following :
sin 90° – cos 0° + tan 0° + tan 45°
Sol :
We know that
Sin (90o) = 1
Cos (0o) = 1
Tan(0o) = 0
Tan(45o) = 1
Now putting the value, we get
= 1 – 1 + 0 + 1
= 1
Question 3 J
Find the numerical value of the following :
$\cos ^{2} 0^{\circ}+\tan ^{2} \frac{\pi}{4}+\sin ^{2} \frac{\pi}{4}$, where π = 180°
Sol :
We know that
Cos (0o) = 1
Tan (45o) = 1 $\left[\frac{\pi}{4}=\frac{180^{\circ}}{4}=45^{\circ}\right]$
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}\left[\frac{\pi}{4}=\frac{180^{\circ}}{4}=45^{\circ}\right]$
Now putting the values;
$=(1)^{2}+(1)^{2}+\left(\frac{1}{\sqrt{2}}\right)^{2}$
$=1+1+\frac{1}{2}$
$=\frac{2+2+1}{2}$
$=\frac{5}{2}$
Question 3 K
Find the numerical value of the following :
$\frac{\cos 60^{\circ}}{\sin ^{2} 45^{\circ}}-3 \cot 45^{\circ}+2 \sin 90^{\circ}$
Sol :
We know that,
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
Cot (45o) = 1
Sin (90o) = 1
Now putting the values, we get
$=\frac{\frac{1}{2}}{\left(\frac{1}{\sqrt{2}}\right)^{2}}-3(1)+2(1)$
= 1-3+2
=0
Question 3 L
Find the numerical value of the following :
$\frac{4}{\tan ^{2} 60^{\circ}}+\frac{1}{\cos ^{2} 30^{\circ}}-\sin ^{2} 45^{\circ}$
Sol :
We can write the above equation as:
= 4 cot2 60o + sec2 30o – sin2 45o …(a) $\left[\because \cos \theta=\frac{1}{\sec \theta}\right.$ and $\left.\tan \theta=\frac{1}{\cot \theta}\right]$
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\cot \left(60^{\circ}\right)=\frac{1}{\sqrt{3}}$
$\operatorname{Sec}\left(30^{\circ}\right)=\frac{2}{\sqrt{3}}$
Now putting the values in (a);
$=4\left(\frac{1}{\sqrt{3}}\right)^{2}+\left(\frac{2}{\sqrt{3}}\right)^{2}-\left(\frac{1}{\sqrt{2}}\right)^{2}$
$=4 \times \frac{1}{3}+\frac{4}{3}-\frac{1}{2}$
$=\frac{8+8-3}{6}$
$=\frac{13}{6}$
Question 3 M
Find the numerical value of the following :
cos60° . cos 30° – sin 60° . sin 30°
Sol :
We know that,
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
Now putting the values, we get
$=\frac{1}{2} \times \frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2} \times \frac{1}{2}$
$=\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{4}$
= 0
Question 3 N
Find the numerical value of the following :
$\frac{4\left(\sin ^{2} 60^{\circ}-\cos ^{2} 45^{\circ}\right)}{\tan ^{2} 30^{\circ}+\cos ^{2} 90^{\circ}}$
Sol :
We know that,
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\tan \left(30^{\circ}\right)=\frac{1}{\sqrt{3}}$
cos(90o) = 0
Now putting the values;
$=4 \times \frac{\left(\frac{\sqrt{3}}{2}\right)^{2}-\left(\frac{1}{\sqrt{2}}\right)^{2}}{\left(\frac{1}{\sqrt{3}}\right)^{2}-(0)^{2}}$
$=4 \times \frac{\frac{3}{4}-\frac{1}{2}}{\frac{1}{3}}$
$=4 \times \frac{1}{4} \times 3$
= 3
Question 4 A
Evaluate the following :
sin30°.cos45° + cos30°.sin45°
Sol :
We know that,
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
Now putting the values, we get
$=\frac{1}{2} \times \frac{1}{\sqrt{2}}+\frac{\sqrt{3}}{2} \times \frac{1}{\sqrt{2}}$
$=\frac{1}{2 \sqrt{2}}+\frac{\sqrt{3}}{2 \sqrt{2}}$
$=\frac{1+\sqrt{3}}{2 \sqrt{2}}$
Question 4 B
Evaluate the following :
cosec230°.tan245° – sec260°
Sol :
We know that
cosec (30o) = 2
Tan(45o) = 1
sec (60 o) = 2
Now putting the values;
= (2)2 × (1)2 – (2)2
= 4 – 4
= 0
Question 4 C
Evaluate the following :
2sin230°.tan60° – 3cos260°.sec230°
Sol :
We know that
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
tan (60o) = √3
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
$\sec \left(30^{\circ}\right)=\frac{2}{\sqrt{3}}$
Now putting the values;
$=2 \times\left(\frac{1}{2}\right)^{2} \times(\sqrt{3})-\left(3 \times\left(\frac{1}{2}\right)^{2} \times\left(\frac{2}{\sqrt{3}}\right)^{2}\right)$
$=2 \times \frac{1}{4} \times(\sqrt{3})-\left(3 \times \frac{1}{4} \times \frac{4}{3}\right)$
$=\frac{\sqrt{3}}{2}-1$
$=\frac{\sqrt{3}-2}{2}$
Question 4 D
Evaluate the following :
tan60° . cosec245° + sec260°.tan45°
Sol :
We know that
tan (60o) = √3
cosec (45o) = √2
sec (60 o) = 2
tan(45o) = 1
Now putting the values;
= (√3) × (√2)2 + (2)2 × (1)
= 2√3 +4
=2 (√3 + 2)
Question 4 E
Evaluate the following :
tan30°.sec45° + tan60°.sin30°
Sol :
We know that
$\tan \left(30^{\circ}\right)=\frac{1}{\sqrt{3}}$
sec (45o) = √2
tan (60o) = √3
$\sec \left(30^{\circ}\right)=\frac{2}{\sqrt{3}}$
Now putting the values, we get
$=\frac{1}{\sqrt{3}} \times \sqrt{2}+\sqrt{3} \times \frac{2}{\sqrt{3}}$
$=\frac{\sqrt{2}}{\sqrt{3}}+2$
$=2+\frac{\sqrt{2}}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$
$=2+\frac{\sqrt{6}}{3}$
Question 4 F
Evaluate the following :
cos30°.cos45° – sin30°.sin45°
Sol :
We know that
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
Now putting the values, we get
$=\frac{\sqrt{3}}{2} \times \frac{1}{\sqrt{2}}-\frac{1}{2} \times \frac{1}{\sqrt{2}}$
$=\frac{\sqrt{3}-1}{2 \sqrt{2}}$
Multiplying and dividing by (√2), we get
$=\frac{\sqrt{3}-1}{2 \sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}$
$=\frac{\sqrt{2}(\sqrt{3}-1)}{4}$
Question 4 G
Evaluate the following :
$\frac{4}{3} \tan ^{2} 30^{\circ}+\sin ^{2} 60^{\circ}-3 \cos ^{2} 60^{\circ}+\frac{3}{4} \tan ^{2} 60^{\circ}-2 \tan ^{2} 45^{\circ}$
Sol :
We know that
$\begin{aligned} \tan \left(30^{\circ}\right) &=\frac{1}{\sqrt{3}} \\ \sin \left(60^{\circ}\right) &=\frac{\sqrt{3}}{2} \\ \cos \left(60^{\circ}\right) &=\frac{1}{2} \end{aligned}$
tan (60o) = √3
tan(45o) = 1
Now putting the values;
$=\left(\frac{4}{3} \times\left(\frac{1}{\sqrt{3}}\right)^{2}\right)+\left[\left(\frac{\sqrt{3}}{2}\right)^{2}\right]-\left[3 \times\left(\frac{1}{2}\right)^{2}\right]+\left[\frac{3}{4}(\sqrt{3})^{2}\right]-\left[2 \times(1)^{2}\right]$
$=\left[\frac{4}{3} \times \frac{1}{3}\right]+\left[\frac{3}{4}\right]-\left[3 \times \frac{1}{4}\right]+\left[\frac{3}{4} \times 3\right]-[2 \times(1)]$
$=\frac{4}{9}+\frac{3}{4}-\frac{3}{4}+\frac{9}{4}-2$
$=\frac{16+27-27+81-72}{36}$
$=\frac{25}{36}$
Question 4 H
Evaluate the following :
$\frac{\tan ^{2} 60^{\circ}+4 \cos ^{2} 45^{\circ}+3 \sec ^{2} 30^{\circ}+5 \cos ^{2} 90^{\circ}}{\operatorname{cosec} 30^{\circ}+\sec 60^{\circ}-\cot ^{2} 30^{\circ}}$
Sol :
We know that
tan (60o) = √3
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\sec \left(30^{\circ}\right)=\frac{2}{\sqrt{3}}$
cos(90o) = 0
cosec (30o) = 2
sec (60 o) = 2
cot (30o) = √3
Now putting the values, we get
$=\frac{(\sqrt{3})^{2}+\left[4 \times\left(\frac{1}{\sqrt{2}}\right)^{2}\right]+\left[3 \times\left(\frac{2}{\sqrt{3}}\right)^{2}\right]+\left[5 \times(0)^{2}\right]}{(2)+(2)-(\sqrt{3})^{2}}$
$=\frac{(3)+\left[4 \times \frac{1}{2}\right]+\left[3 \times \frac{4}{3}\right]+[5 \times 0]}{2+2-3}$
$=\frac{(3)+[2]+[4]+[0]}{2+2-3}$
= 9
Question 4 I
Evaluate the following :
$\frac{5 \sin ^{2} 30^{\circ}+\cos ^{2} 45^{\circ}-4 \tan ^{2} 30^{\circ}}{2 \sin 30^{\circ} \cdot \cos 30^{\circ}+\tan 45^{\circ}}$
Sol :
We know that
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\tan \left(30^{\circ}\right)=\frac{1}{\sqrt{3}}$
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
tan (45o) = 1
Now putting the values, we get
$=\frac{\left[5 \times\left(\frac{1}{2}\right)^{2}\right]+\left(\frac{1}{\sqrt{2}}\right)^{2}-\left[4 \times\left(\frac{1}{\sqrt{3}}\right)^{2}\right]}{2\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right)+(1)}$
$=\frac{\left(\frac{5}{4}\right)+\left(\frac{1}{2}\right)-\left(\frac{4}{3}\right)}{\left(\frac{\sqrt{3}}{2}\right)+1}$
$=\frac{\left(\frac{15+6-16}{12}\right)}{\left(\frac{\sqrt{3}+2}{2}\right)}$
$=\frac{5}{12} \times \frac{2}{\sqrt{3}+1}$
$=\frac{5}{6} \times \frac{1}{\sqrt{3}+2}$
Question 5 A
Prove the following :
$\frac{(1-\cos B)(1+\cos B)}{(1-\sin B)(1+\sin B)}=\frac{1}{3}$ When B = 30°
Sol :
Solving, L.H.S.
$=\frac{(1)^{2}-(\cos B)^{2}}{(1)^{2}-(\sin B)^{2}}$ [(a)2 – (b)2 = (a+b)(a-b)]
$=\frac{1-\cos ^{2} B}{1-\sin ^{2} B}$
We know that,
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
Putting the values, we get
$=\frac{1-\left(\frac{\sqrt{3}}{2}\right)^{2}}{1-\left(\frac{1}{2}\right)^{2}}$
$=\frac{1-\frac{3}{4}}{1-\frac{1}{4}}$
$=\frac{4-3}{4-1}$
$=\frac{1}{3}$
=R.H.S.
Hence Proved
Question 5 B
Prove the following :
$\frac{(1-\cos \alpha)(1+\cos \alpha)}{(1-\sin \alpha)(1+\sin \alpha)}=3$ When α =60°
Sol :
Solving, L.H.S.
$=\frac{(1)^{2}-(\cos \alpha)^{2}}{(1)^{2}-(\sin \alpha)^{2}}$ [(a)2 – (b)2 = (a+b)(a-b)]
$=\frac{1-\cos ^{2} \alpha}{1-\sin ^{2} \alpha}$
We know that
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
Putting the values, we get
$=\frac{1-\left(\frac{1}{2}\right)^{2}}{1-\left(\frac{\sqrt{3}}{2}\right)^{2}}$
$=\frac{1-\frac{1}{4}}{1-\frac{3}{4}}$
$=\frac{4-1}{4-3}$
= 3 = R.H.S.
Question 5 C
Prove the following :
cos(A – B) = cos A. cos B + sinA . sin B if A=B=60o
Sol :
Solving, L.H.S.
= cos (60o – 60o) [Putting the value A=B=60o]
= cos (0o)
= 1
Solving, R.H.S.
= cos (60o) × cos (60o) + sin (60o) × sin (60o) [Putting the value A=B=60o]
= cos2(60o) + sin2(60o)
We know that,
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
$=\left(\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}$
$=\frac{1}{4}+\frac{3}{4}$
$=\frac{1+3}{4}$
= 1
∴ LHS = RHS
Hence Proved
Question 5 D
Prove the following :
4(sin430° + cos4 60°) – 3(cos2 45° – sin290°) = 2
Sol :
We know that,
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
Sin (90o) = 1
= 4[{(sin 30o)2}2 + {(cos 60o)2}2] – 3[(cos 45o)2 – (sin 90o)2]
Putting the values
$=4 \times\left[\left\{\left(\frac{1}{2}\right)^{2}\right\}^{2}+\left\{\left(\frac{1}{2}\right)^{2}\right\}^{2}\right]-3\left[\left(\frac{1}{\sqrt{2}}\right)^{2}-1\right]$
$=4 \times\left[\left\{\frac{1}{4}\right\}^{2}+\left\{\frac{1}{4}\right\}^{2}\right]-3\left[\frac{1}{2}-1\right]$
$=4 \times\left[\frac{1}{16}+\frac{1}{16}\right]-3\left[-\frac{1}{2}\right]$
$=4 \times\left[\frac{1}{8}\right]-3\left[-\frac{1}{2}\right]$
$=\left[\frac{1}{2}\right]+\left[\frac{3}{2}\right]$
$=\left[\frac{4}{2}\right]$
=2 = R.H.S.
Hence Proved
Question 5 E
Prove the following :
sin90° = 2sin45°.cos45°
Sol :
We know that,
sin (90o) = 1
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
Taking LHS = sin 90° = 1
Now, taking RHS
$=2 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}$
$=2 \times \frac{1}{2}$
= 1
= R.H.S.
Hence Proved
Question 5 F
Prove the following :
cos60° = 2cos230° – 1 = 1 – 2 sin230°
Sol :
We know that,
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
Taking LHS = cos 60° $=\frac{1}{2}$
Now, solving RHS = 2cos2 30° – 1 , we get
$=2 \times\left(\frac{\sqrt{3}}{2}\right)^{2}-1$
$=2 \times \frac{3}{4}-1$
$=\frac{3}{2}-1$
$=\frac{3}{2}-1$
$=\frac{1}{2}$
= RHS
Now taking RHS = 1- 2sin2 30°
$=1-2\left(\frac{1}{2}\right)^{2}$
$=1-\frac{1}{2}$
$=\frac{2-1}{2}$
$=\frac{1}{2}$
= RHS
Hence, proved.
Question 5 G
Prove the following :
cos90° = 1 – 2 sin245° = 2cos245° – 1
Sol :
We know that
cos(90o) = 0
$\sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
$\cos \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}$
taking LHS = cos 90° = 0
Now solving RHS 1- 2sin2 45°
$=1-2\left(\frac{1}{\sqrt{2}}\right)^{2}$
$=1-2 \times \frac{1}{2}$
= 1- 1
= 0
= RHS
Now, solving RHS = 2cos2 45° – 1 , we get
$=1-2 \times\left(\frac{1}{\sqrt{2}}\right)^{2}$
$=1-2 \times \frac{1}{2}$
= 1- 1
= 0
Hence, proved.
Question 5 H
Prove the following :
sin30°.cos60° + cos30°.sin60° = sin90°
Sol :
We know that
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
sin (90o) = 1
Taking LHS =
$=\left[\left(\frac{1}{2}\right) \times\left(\frac{1}{2}\right)\right]+\left[\left(\frac{\sqrt{3}}{2}\right) \times\left(\frac{\sqrt{3}}{2}\right)\right]$
$=\left[\left(\frac{1}{4}\right)\right]+\left[\left(\frac{3}{4}\right)\right]$
$=\left[\frac{1+3}{4}\right]$
= 1
Now, RHS = sin 90° = 1
∴ LHS = RHS
Hence, proved.
Question 5 I
Prove the following :
cos60°.cos30° – sin60°. sin30° = cos 90°
Sol :
We know that
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
cos(90o) = 0
Taking LHS
$=\left[\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right)\right]-\left[\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{2}\right)\right]$
$=\left[\left(\frac{\sqrt{3}}{4}\right)\right]-\left[\left(\frac{\sqrt{3}}{4}\right)\right]$
= 0
∴ LHS =RHS
Hence, proved.
Question 5 J
Prove the following :
$\cos 60^{\circ}=\frac{1-\tan ^{2} 30^{\circ}}{1+\tan ^{2} 30^{\circ}}$
Sol :
We know that,
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
$\tan \left(30^{\circ}\right)=\frac{1}{\sqrt{3}}$
Taking LHS = $\cos 60^{\circ}=\frac{1}{2}$
Now, solving RHS
$=\frac{1-\left(\frac{1}{\sqrt{3}}\right)^{2}}{1+\left(\frac{1}{\sqrt{3}}\right)^{2}}$
$=\frac{1-\frac{1}{3}}{1+\frac{1}{3}}$
$=\frac{\frac{3-1}{3}}{\frac{3+1}{3}}$
$=\frac{2}{4}$
$=\frac{1}{2}$
∴ L.H.S. = R.H.S.
Hence, proved.
Question 5 K
Prove the following :
$\frac{\tan 60^{\circ}-\tan 30^{\circ}}{1+\tan 60^{\circ} \cdot \tan 30^{\circ}}=\tan 30^{\circ}$
Sol :
We know that
tan(60o) = √3
$\tan \left(30^{\circ}\right)=\frac{1}{\sqrt{3}}$
Taking LHS
$=\frac{\sqrt{3}-\frac{1}{\sqrt{3}}}{1+(\sqrt{3}) \times\left(\frac{1}{\sqrt{3}}\right)}$
$=\frac{\frac{3-1}{\sqrt{3}}}{1+1}$
$=\frac{\frac{2}{\sqrt{3}}}{2}$
$=\frac{1}{\sqrt{3}}$
Now, RHS $=\tan 30^{\circ}=\frac{1}{\sqrt{3}}$
∴L.H.S. = R.H.S.
Hence, proved.
Question 5 L
Prove the following :
$\frac{1-\tan 30^{\circ}}{1+\tan 30^{\circ}}=\frac{1-\sin 60^{\circ}}{\cos 60^{\circ}}$
Sol :
$\tan \left(30^{\circ}\right)=\frac{1}{\sqrt{3}}$
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
Taking LHS
$=\frac{1-\frac{1}{\sqrt{3}}}{1+\frac{1}{\sqrt{3}}}$
$=\frac{\frac{\sqrt{3}-1}{\sqrt{3}}}{\frac{\sqrt{3}+1}{\sqrt{3}}}$
$=\frac{\sqrt{3}-1}{\sqrt{3}+1}$
Multiplying and Dividing, LHS by (√3- 1)
$=\frac{\sqrt{3}-1}{\sqrt{3}+1} \times \frac{\sqrt{3}-1}{\sqrt{3}-1}$
$=\frac{(\sqrt{3}-1)^{2}}{(\sqrt{3})^{2}-(1)^{2}}$ [(a)2 – (b)2 = (a+b)(a-b)]
$=\frac{(\sqrt{3}-1)^{2}}{(\sqrt{3})^{2}-(1)^{2}}$
$=\frac{3+1-2 \sqrt{3}}{3-1}$
$=\frac{4-2 \sqrt{3}}{2}$
Multiplying and Dividing, LHS by 2
= 2- √3
Now, RHS
$=\frac{1-\frac{\sqrt{3}}{2}}{\frac{1}{2}}$
$=\frac{\frac{2-\sqrt{3}}{2}}{\frac{1}{2}}$
= 2- √3
∴ LHS = RHS
Hence, proved.
Question 5 M
Prove the following :
$\frac{\sin 60^{\circ}+\cos 30^{\circ}}{\sin 30^{\circ}+\cos 60^{\circ}+1}=\cos 30^{\circ}$
Sol :
We know that
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\cos \left(60^{\circ}\right)=\frac{1}{2}$
Taking LHS
$=\frac{\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}}{\frac{1}{2}+\frac{1}{2}+1}$
$=\frac{2 \times \frac{\sqrt{3}}{2}}{\frac{1+1+2}{2}}$
$=\frac{\sqrt{3}}{2}$
Now, RHS= $\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
∴ LHS =RHS
Hence Proved
Question 5 N
Prove the following :
$\sin 60^{\circ}=2 \sin 30^{\circ} \cdot \cos 30^{\circ}=\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}$
Sol :
We know that
$\sin \left(30^{\circ}\right)=\frac{1}{2}$
$\sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}$
$\tan \left(30^{\circ}\right)=\frac{1}{\sqrt{3}}$
Taking LHS $=\sin 60^{\circ}=\frac{\sqrt{3}}{2}$
Now, solving RHS = 2 sin 30° cos 30°
$=2 \times \frac{1}{2} \times \frac{\sqrt{3}}{2}$
$=\frac{\sqrt{3}}{2}$
= LHS
Now, RHS$=\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}$
$=\frac{2\left(\frac{1}{\sqrt{3}}\right)}{1+\left(\frac{1}{\sqrt{3}}\right)^{2}}$
$=\frac{\frac{2}{\sqrt{3}}}{1+\frac{1}{3}}$
$=\frac{\frac{2}{\sqrt{3}}}{\frac{4}{3}}$
$=\frac{2}{\sqrt{3}} \times \frac{3}{4}$
$=\frac{\sqrt{3}}{2}$
∴ LHS =RHS
Hence proved
Question 6A
If A=60o and B = 30o, verify that :
cos (A+B) = cos A cos B – sin A sin B
Sol :
Given: A=60o and B =30o
Now, LHS = Cos (A+B)
⇒ Cos (60 o + 30 o)
⇒ Cos (90 o)
⇒ 0 [∵ cos 90 o = 0]
Now, RHS = Cos A Cos B – Sin A Sin B
⇒ cos(60 o) cos(30 o) – sin(60 o) sin (30 o)
$\Rightarrow\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right)-\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{2}\right)$
⇒ 0
∴ LHS = RHS
Hence Proved
Question 6 B
If A=60o and B = 30o, verify that :
sin (A – B) = sin A cos B – cos A sin B
Sol :
Given: A=60o and B =30o
Now, LHS = Sin (A-B)
⇒ Sin (60 o – 30 o)
⇒ Sin (30 o)
$\Rightarrow\left(\frac{1}{2}\right)$
Now, RHS = Sin A Cos B – Cos A Sin B
⇒ sin(60 o) cos(30 o) – cos(60 o) sin (30 o)
$\Rightarrow\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)-\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)$
$\Rightarrow \frac{3}{4}-\frac{1}{4}$
$\Rightarrow\left(\frac{1}{2}\right)$
∴ LHS = RHS
Hence Proved
Question 6 C
If A=60o and B = 30o, verify that :
tan (A – B) $=\frac{\tan A-\tan B}{1+\tan A \tan B}$
Sol :
Given: A=60o and B =30o
Now, LHS = tan (A-B)
⇒ tan (60 o – 30 o)
⇒ tan (30 o)
$\Rightarrow\left(\frac{1}{\sqrt{3}}\right)$
Now, RHS $=\frac{\tan A-\tan B}{1+\tan A \tan B}$
$=\frac{\tan 60^{\circ}-\tan 30^{\circ}}{1+\tan 60^{\circ} \tan 30^{\circ}}$
$\Rightarrow \frac{\sqrt{3}-\left(\frac{1}{\sqrt{3}}\right)}{1+(\sqrt{3})\left(\frac{1}{\sqrt{3}}\right)}$
$\Rightarrow \frac{\frac{3-1}{\sqrt{3}}}{1+1}$
$\Rightarrow\left(\frac{1}{\sqrt{3}}\right)$
∴ LHS = RHS
Hence Proved
Question 7 A
If A = 30o, verify that :
sin 2A = 2 sin A cos A
Sol :
Given: A =30o
Now, LHS = sin 2(30o)
⇒ sin 60o
$\Rightarrow \frac{\sqrt{3}}{2}$
Now, RHS = 2 sin A cos A
⇒ 2 sin (30o) cos (30o)
$\Rightarrow 2\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right)$
$\Rightarrow \frac{\sqrt{3}}{2}$
∴ LHS = RHS
Hence Proved
Question 7 B
If A = 30o, verify that :
cos 2A = 1-2 sin2A=2cos2 A – 1
Sol :
Given: A =30o
Now, LHS = cos 2(30o)
⇒ cos 60o
$\Rightarrow \frac{1}{2}$
Now, RHS = 1- 2sin2 A
⇒ 1- 2sin2 (30o)
$\Rightarrow 1-2\left(\frac{1}{2}\right)^{2}$
$\Rightarrow 1-2\left(\frac{1}{4}\right)$
$\Rightarrow \frac{2-1}{2}$
$\Rightarrow \frac{1}{2}$
Now, RHS = 2cos2 A – 1
⇒ 2cos2 (30o) – 1
$\Rightarrow 2\left(\frac{\sqrt{3}}{2}\right)^{2}-1$
$\Rightarrow 2\left(\frac{3}{4}\right)-1$
$\Rightarrow \frac{3-2}{2}$
$\Rightarrow \frac{1}{2}$
∴ LHS = RHS
Hence Proved
Question 8 A
If θ = 30°, verify that :
sin 3θ = 3 sinθ – 4 sin3θ
Sol :
Given: θ =30o
Now, LHS = sin 3(30o)
⇒ sin 90o
= 1
Now, RHS = 3 sin θ – 4 sin3 θ
⇒ 3 sin (30o) – 4 sin3 (30o)
$\Rightarrow 3\left(\frac{1}{2}\right)-4\left(\frac{1}{2}\right)^{3}$
$\Rightarrow \frac{3}{2}-\frac{1}{2}$
= 1
∴ LHS = RHS
Hence Proved
Question 8 B
If θ = 30°, verify that :
cos3θ = 4cos3θ – 3cosθ
Sol :
Given: θ =30o
Now, LHS = cos 3(30o)
⇒ cos 90o
= 0
Now, RHS = 4 cos3 θ – 3 cos θ
⇒ 4 cos3 (30o) – 3 cos (30o)
$\Rightarrow 4\left(\frac{\sqrt{3}}{2}\right)^{3}-3\left(\frac{\sqrt{3}}{2}\right)$
$\Rightarrow\left(\frac{3 \sqrt{3}}{2}\right)-\left(\frac{3 \sqrt{3}}{2}\right)$
= 0
∴ LHS = RHS
Hence Proved
Question 9
If sin (A + B) = 1 and cos (A – B) = $\frac{\sqrt{3}}{2}$, then find A and B.
Sol :
Given : sin (A+B) =1
⇒ Sin(A+B) = sin (90 o) [∵ sin (90 o)=1]
On equating both the sides, we get
A + B = 90 o …(1)
And $\cos (A-B)=\frac{\sqrt{3}}{2}$
⇒ cos(A – B) = cos (30 o) $\left[\because \cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}\right]$
On equating both the sides, we get
A – B = 30 o …(2)
On Adding Eq. (1) and (2), we get
2A = 120 o
⇒ A = 60 o
Now, Putting the value of A in Eq.(1), we get
60 o + B =90 o
⇒ B = 30 o
Hence, A = 60 o and B = 30 o
Question 10
If sin (A + B) = 1 and cos (A – B) = 1, find A and B.
Sol :
Given : sin (A+B) =1
⇒ Sin(A+B) = sin (90 o) [∵ sin (90 o) =1]
On equating both the sides, we get
A + B = 90 o …(1)
And cos (A – B) = 1
⇒ cos(A – B) = cos (0 o) [∵ cos(0 o) = 1]
On equating both the sides, we get
A – B = 0 o …(2)
On Adding Eq. (1) and (2), we get
2A = 90 o
⇒ A = 45 o
Now, Putting the value of A in Eq.(1), we get
45 o + B =90 o
⇒ B = 45 o
Hence, A = 45 o and B = 45 o
Question 11
If sin (A + B) = cos (A – B) = $\frac{\sqrt{3}}{2}$, fins A and B.
Sol :
Given : $\sin (A+B)=\frac{\sqrt{3}}{2}$
⇒ Sin(A+B) = sin (60 o) $\left[\because \sin (60 ^{\circ})=\frac{\sqrt{3}}{2}\right]$
On equating both the sides, we get
A + B = 60 o …(1)
And $\cos (A-B)=\frac{\sqrt{3}}{2}$
⇒ cos(A – B) = cos (30 o) $\left[\because \cos (30^{\circ})=\frac{\sqrt{3}}{2}\right]$
On equating both the sides, we get
A – B = 30 o …(2)
On Adding Eq. (1) and (2), we get
2A = 90 o
⇒ A = 45 o
Now, Putting the value of A in Eq.(1), we get
45 o + B =60 o
⇒ B = 15 o
Hence, A = 45 o and B = 15 o
Question 12
If sin (A – B) = 1/2, cos(A + B) = 1/2; 0o<A+B<90o; A > B, find A and B.
Sol :
Given : $\sin (A-B)=\frac{1}{2}$
⇒ Sin(A-B) = sin (30 o) $\left[\because \sin (30^{\circ})=\frac{1}{2}\right]$
On equating both the sides, we get
A – B = 30 o …(1)
And $\cos (A+B)=\frac{1}{2}$
⇒ cos(A + B) = cos (60 o) $\left[\because \cos (60^{\circ})=\frac{1}{2}\right]$
On equating both the sides, we get
A + B = 60 o …(2)
On Adding Eq. (1) and (2), we get
2A = 90 o
⇒ A = 45 o
Now, Putting the value of A in Eq.(2), we get
45 o + B =60 o
⇒ B = 15 o
Hence, A = 45 o and B = 15 o
Question 13 A
Show by an example that
cos A – cos B ≠ cos (A – B)
Sol :
Let A = 60o and B = 30o, then
L.H.S. =cos A-cosB
=cos60°-cos30°
$=\frac{1}{2}-\frac{\sqrt{3}}{2}=\frac{1-\sqrt{3}}{2}$
R. H. S=cos(A-B)
=cos(60°-30°)
$=\cos 30^{\circ}=\frac{\sqrt{3}}{2}$
∴ L.H.S. ![]() R.H.S
R.H.S
Question 13 B
Show by an example that
cos C + cos D ≠ cos (C + D)
Sol :
Let C = 60o and D = 30o, then
L.H.S. = cos C + cos D = cos 60o + cos 30o
$=\frac{1}{2}+\frac{\sqrt{3}}{2}=\frac{1+\sqrt{3}}{2}$
R. H. S. = cos (C+D) = cos (60o + 30o) = cos 90o= 0
∴ L.H.S. ![]() R.H.S
R.H.S
Question 13 C
Show by an example that
sin A + sin B ≠ sin (A + B)
Sol :
Let A = 60o and B = 30o, then
L.H.S. = sin A + sin B = sin 60o + sin 30o
$=\frac{\sqrt{3}}{2}+\frac{1}{2}=\frac{\sqrt{3}+1}{2}$
R. H. S. = sin (A + B) = sin (60o + 30o) = sin 90o =1
∴ L.H.S. ![]() R.H.S
R.H.S
Question 13 D
Show by an example that
sin A – sin B ≠ sin (A – B)
Sol :
Let A = 60o and B = 30o, then
L.H.S. = sin A – sin B = sin 60o – sin 30o
$=\frac{\sqrt{3}}{2}-\frac{1}{2}=\frac{\sqrt{3}-1}{2}$
R. H. S. = sin (A – B) = sin (60o – 30o) = sin 30o
$=\frac{1}{2}$
∴ L.H.S. ≠R.H.S
Question 14
In a right ΔABC hypotenuse AC = 10 cm and ∠A = 60°, then find the length of the remaining sides.
Sol :
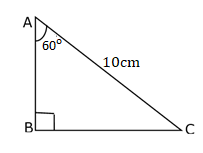
Given: ∠A = 60o and AC = 10cm
Now, $\sin 60^{\circ}=\frac{\text { Perpendicular }}{\text { Hypotenuse }}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{BC}}{10}$
Now, we know that $\sin 60^{\circ}=\frac{\sqrt{3}}{2}$
$\Rightarrow \frac{\sqrt{3}}{2}=\frac{B C}{10}$
⇒ BC = 5√3 cm
In right angled ∆ABC , we have
⇒ (AB)2 + (BC)2 =(AC)2 [by using Pythagoras theorem]
⇒ (AB)2 + (5√3)2 = (10)2
⇒ (AB)2 +(25×3) =100
⇒ (AB)2 +75 = 100
⇒ (AB)2 = 100 – 75
⇒ (AB)2 = 25
⇒ AB =√25
⇒ AB = ±5
⇒ AB = 5cm [taking positive square root since, side cannot be negative]
∴ Length of the side AB = 5cm and BC =5√3 cm
Question 15
In a rectangle ABCD, BD : BC = 2 : √3, then find ∠BDC in degrees.
Sol :
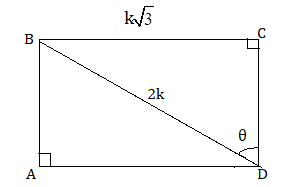
Given BD: BC = 2 : √3
We have to find the ∠BDC
We know that,
$\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\Rightarrow \sin \theta=\frac{k \sqrt{3}}{2 k}$
$\Rightarrow \sin \theta=\frac{\sqrt{3}}{2}$
⇒ sin θ = sin 60o
⇒ θ = 60o
